👨‍🏫학습목표

오늘은 Optimal Policy를 찾기 위한 Optimal value function, Bellman optimality equation에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=WoJoB1D69cA&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=6

1️⃣ Optimal policy의 정의

Optimal value function들 중 value가 가장 큰 함수를 optimal value function이라고 하고, optimal value function을 구하는 것이 Markov Decision Process의 해를 구하는 것이다.

🔷 Optimal state value function

• 각 state에 대해서 state value function값이 최대가 되도록 하는 policy를 적용한 state value function

🔷 Optimal action value function

$q_*(s, a) = \max_\pi q_\pi(s, a)$

• 각 state와 action pair에 대해서 action value function값이 최대가 되도록 하는 policy를 적용한 action value function
• Optimal policy를 찾기 위한 필수적인 값이다.

🔻 그런데 각 state나 state, action pair마다 value가 최대가 되는 policy가 다르면 optimal policy를 어떻게 찾나요?

그런 경우는 순서를 비교할 수 없다.

$\pi' \geq \pi \ \ \text{ if } \ v_{\pi'}(s) \geq v_\pi(s) \ \text{ for all } s.$

Optimal policy를 모든 state에서 value값이 비교하는 policy보다 커야 한다.

🔷 Theorem: Existence of Optimal Policies

Any MDP satisfies the followings.

• There exists an optimal policy $\pi_* \geq \pi \ \ \text{for all} \ \ \pi$
• All optimal policies achieve the optimal state-value function $v_{\pi_*}(s) = v_*(s).$
• All optimal policies achieve the optimal action-value function $q_{\pi_*}(s, a) = q_*(s, a).$

---

2️⃣ Optimal policy를 구하기 위해 알아야 할 것

🔷 Optimal policy

$\pi_*(a|s) = \begin{cases} 1 & \text{if } a = \arg \max_a q_*(s,a) \\ 0 & \text{otherwise} \end{cases}$

• Action-value function의 값을 최대화하는 action을 취할 확률을 1로 한다.
• 따라서 우리가 $q_*(s,a)$를 찾을 수만 있다면 optimal policy를 찾을 수 있다.

$v_*(s) = \max_a q_*(s,a) \ \ by \ \ v_*(s) = \sum_a \pi_*(a|s) q_*(s,a)$

• 최적의 action에서 $\pi_*(a|s) = 1$ 이므로 optimal state-value function은 위와 같이 정리할 수 있다.
• 위 식을 통해 Optimal action-value function $q_*(s,a)$을 알면 optimal state-value function $v_*(s)$을 알 수 있다는 것을 확인할 수 있다.
• 강화학습에서는 random sample을 이용하여 $q_*(s,a)$의 추정치를 계산한다.

---

3️⃣ Bellman optimality equation

• 두 식 모두 Bellman expectation equation에서 optimal policy를 적용한 식이다.
• 식을 분해하였을 때, $\pi(a|s) = 1$ 을 적용하면 아래의 식들이 유도된다.

🔷 Dynamic Programming

$v_*(s) = \max_a \sum_{s',r} p(s', r | s, a) [r + \gamma v_*(s')]$

$q_*(s, a) = \sum_{s',r} p(s', r | s, a) [r + \gamma \max_{a'} q_*(s', a')]$

• 각 수식을 보면 $p(s', r | s, a)$와 value function을 알 때, 현재 value function을 계산할 수 있음을 확인할 수 있다.
• 해당 식들은 서로 의존적이기 때문에 하나의 값만 알아서는 계산할 수 없다.
• 일반적으로 $p(s', r | s, a)$를 알고 있는 경우를 Model-based라고 한다.

---

4️⃣ Bellman Optimality Equation의 Backup Diagram

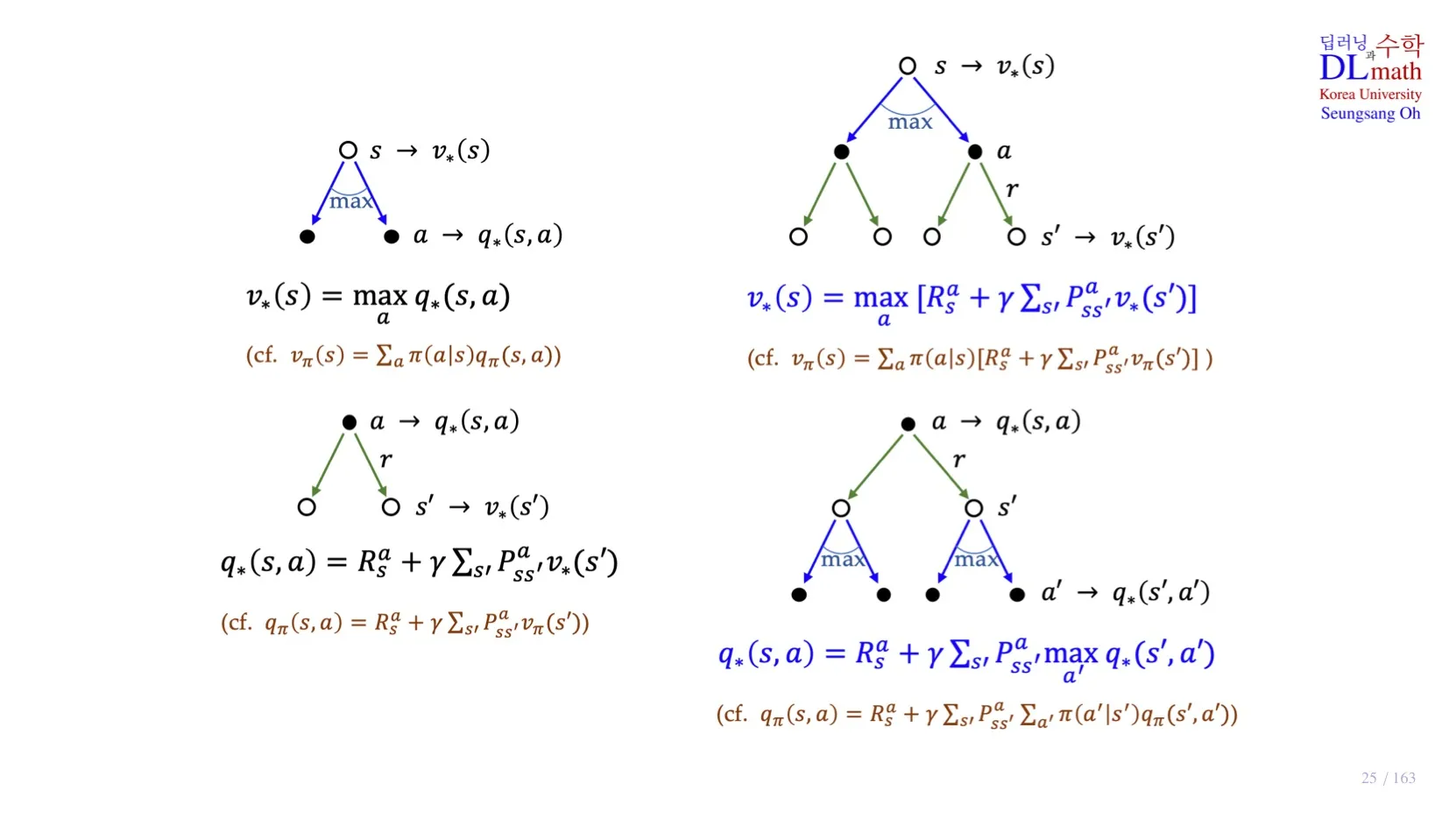
Optimal expectation과 마찬가지로 분해한 두 식을 각각 서로 다른 식으로 채워넣으면 아래의 두 식이 유도된다.

$v_*(s) = \max_a [R_s^a + \gamma \sum_{s'} P_{ss'}^a v_*(s')]$

$q_*(s, a) = R_s^a + \gamma \sum_{s'} P_{ss'}^a \max_{a'} q_*(s', a')$

---

5️⃣ 정리

🔷 6강에서 배운 내용은 아래와 같다.

1. Optimal policy의 정의에 대해 배웠다.
2. Optimal policy를 구하기 위해 $q_*(s,a)$를 알아야 한다.
3. Bellman Optimality Equation에 대해 배웠다.
4. Dynamic Programming을 계산하기 위해서는 $p(s', r | s, a)$를 알아야 한다.