👨‍🏫학습목표

오늘은 Dynamic programming의 정의와 특징과 Reinforcement의 종류에 대해 배울 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=4i_ycR6uCdQ&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=7

1️⃣ Dynamic Programming

🔷 Dynamic programming (DP)이란?

• 복잡한 문제를 여러 개의 간단한 문제로 나누어서 효율적으로 계산하는 방법이다.

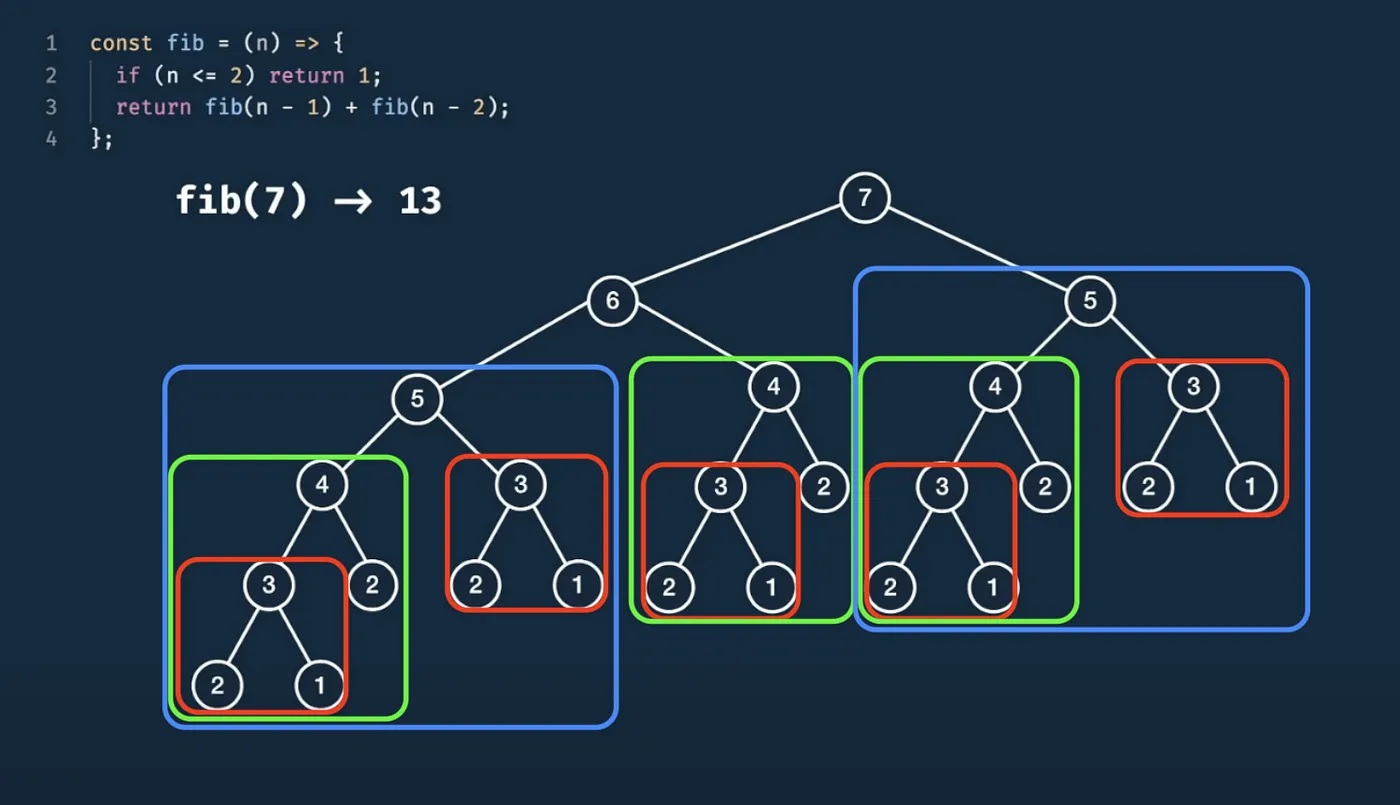
출처: https://matthewaquino.medium.com/intro-to-dynamic-programming-with-the-fibonacci-sequence-d9005e577854

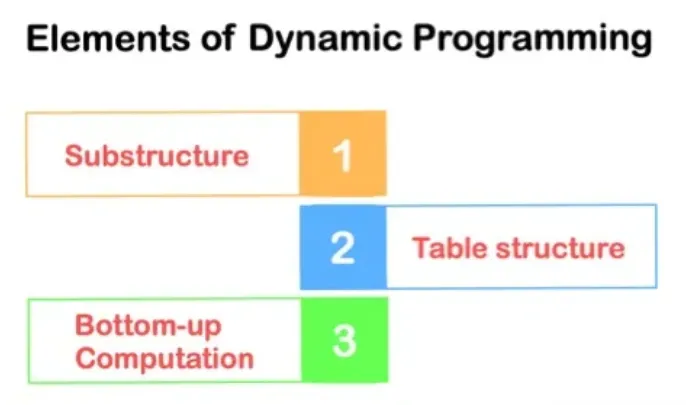
🔻 Substructure

• 복잡한 문제를 여러 개의 단순한 문제로 분해하는 단계이다.

🔻 Table Structure

• 분해된 작은 문제들의 답을 구한 후, 해답들을 하나의 표에 정리하는 단계이다.

🔻 Bottom-up Computation

• 작은 문제들의 해답을 이용해서 조금 더 큰 문제를 풀고, 이 방식을 통해 원래의 복잡한 문제를 해결하는 단계이다.

🔷 DP를 적용하는 문제의 특징

🔻 Optimal substructure

• 우리가 구하고 싶은 문제의 optimal solution이 작은 문제들의 optimal solution을 통해 구할 수 있는 경우.
• 가장 짧은 경로로 출발점에서 도착점으로 이동하고 싶은 경우.

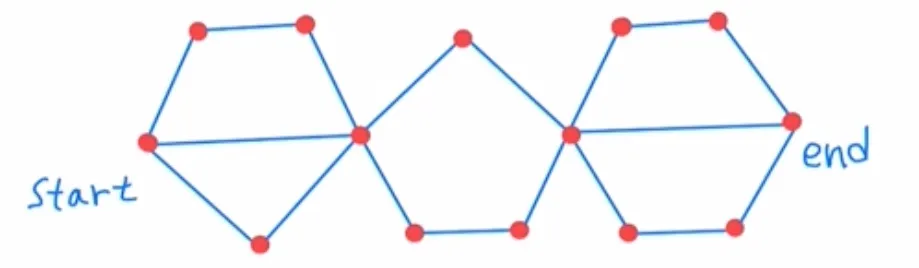
🔻 Overlapping sub-problems

• 우리가 구하고 싶은 문제의 optimal solution을 구하기 위해서 작은 문제들의 optimal solution이 반복적으로 사용되는 경우.
• 이 특징에 따르면 위 그림의 예시는 DP 문제에 해당하지 않는다.

🔷 Markov Decision Process에 DP 적용

🔻 Bellman Equation

• Bellman equation을 통해 problem을 recursive하게 분해할 수 있다.
• $v_\pi$를 모르기 때문에, 현재 value state function $v_k$에서 $v_{k+1}$로 업데이트 하면서 $v_\pi$를 구한다.

🔻 Value function

• 각 Value function들이 최종 solution을 위해 기록되었다가 반복적으로 사용된다.
• 각 $v_\pi$, $v_{k+1}$ 기록해 두었다가 사용한다.

❗주의사항

• 해당 Dynamic programming을 적용하기 위해서는 state transition probability를 알고 있어야 한다.

---

2️⃣ Sequential Decision Problem

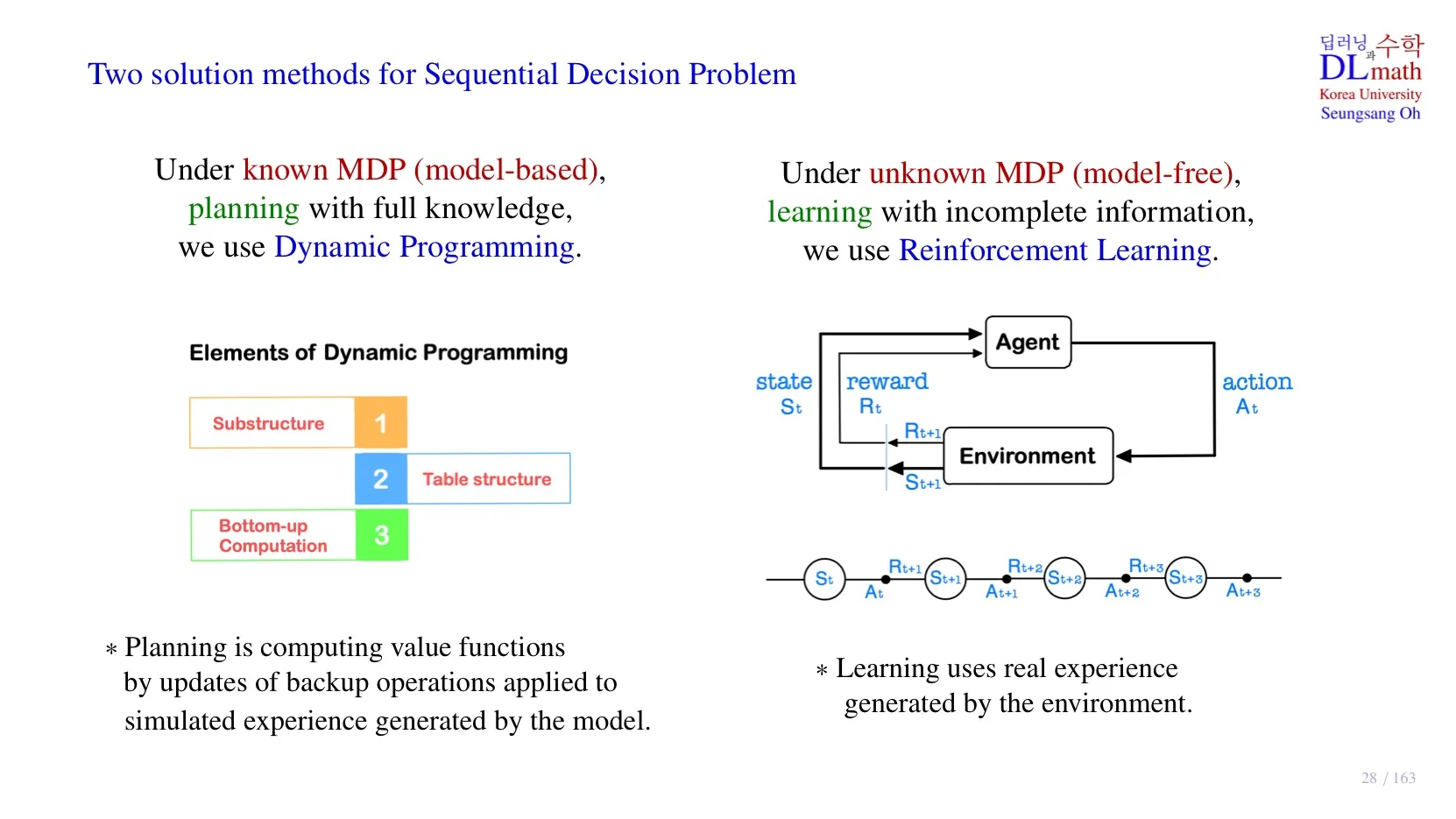
🔷 Sequential Decision Problem

• 순차적 행동 결정 문제로, 각 시간마다 어떤 행동을 해야하는지 결정해야 하는 문제이다.
• Markove Decision Process로 이해해도 무방하다.
• 이러한 Markov Decision Process를 해결할 수 있는 방법이 Dynamic Programming과 Reinforcement Learning이다.
• 두 방법의 가장 큰 차이점은 transition probability $p(s' | s,a)$와 그때의 reward $r(s,a)$를 알고 있는지의 여부이다.

🔻 Dynamic Programming

• Known MDP (model-based)
• $p(s' | s,a)$, $r(s,a)$를 알고 있는 경우.
• Planning: 시행착오 없이 알고 있는 정보를 토대로 optimal policy를 구한다.

😅 Dynamic programming의 한계점

• Computational Complexity: 원래 문제가 복잡하기 때문에 계산 복잡도가 높다.
• Curse of Dimensionality: state를 table에 저장할 때, state의 차원이 너무 크면 table에 모두 저장할 수 없다.
• Knowledge of Environment Model: state transition probability와 그에 대한 reward에 대해 완벽하게 알아야 한다.

🔻 Reinforcement Learning

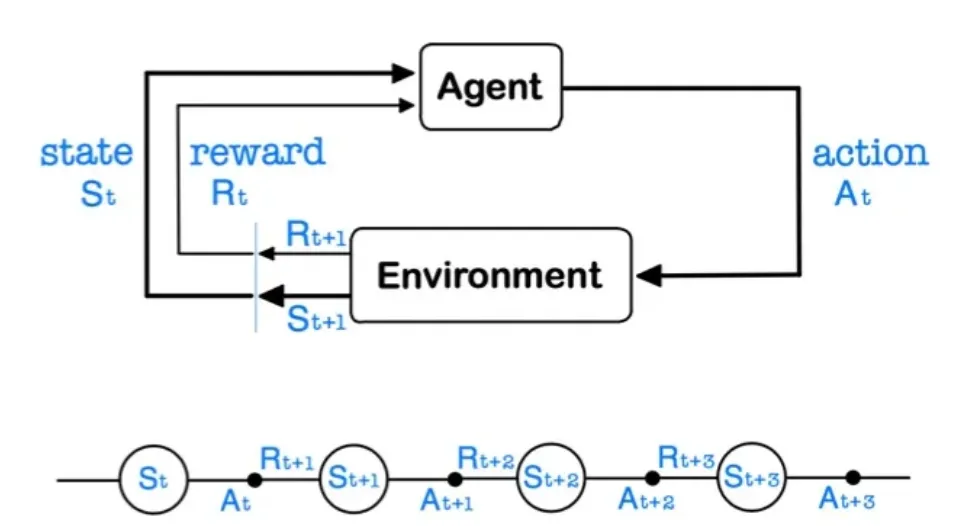
• Unknown MDP (model-free)
• $p(s' | s,a)$, $r(s,a)$를 모르는 경우.
• Learning: 환경 속에서 얻은 경험을 통해 optimal policy를 구한다.
• $s,a \rightarrow s', r$의 경험을 통해 데이터를 구한 후, 이러한 데이터를 쌓아 $p(s'|s,a)$를 추정한다.
• 모든 state가 아닌 sample $s,a \rightarrow s', r$에 대해서만 계산을 할 수 있기 때문에, 계산복잡도나 차원의 저주 문제를 해결할 수 있다.

---

3️⃣ Reinforcement Learning의 종류

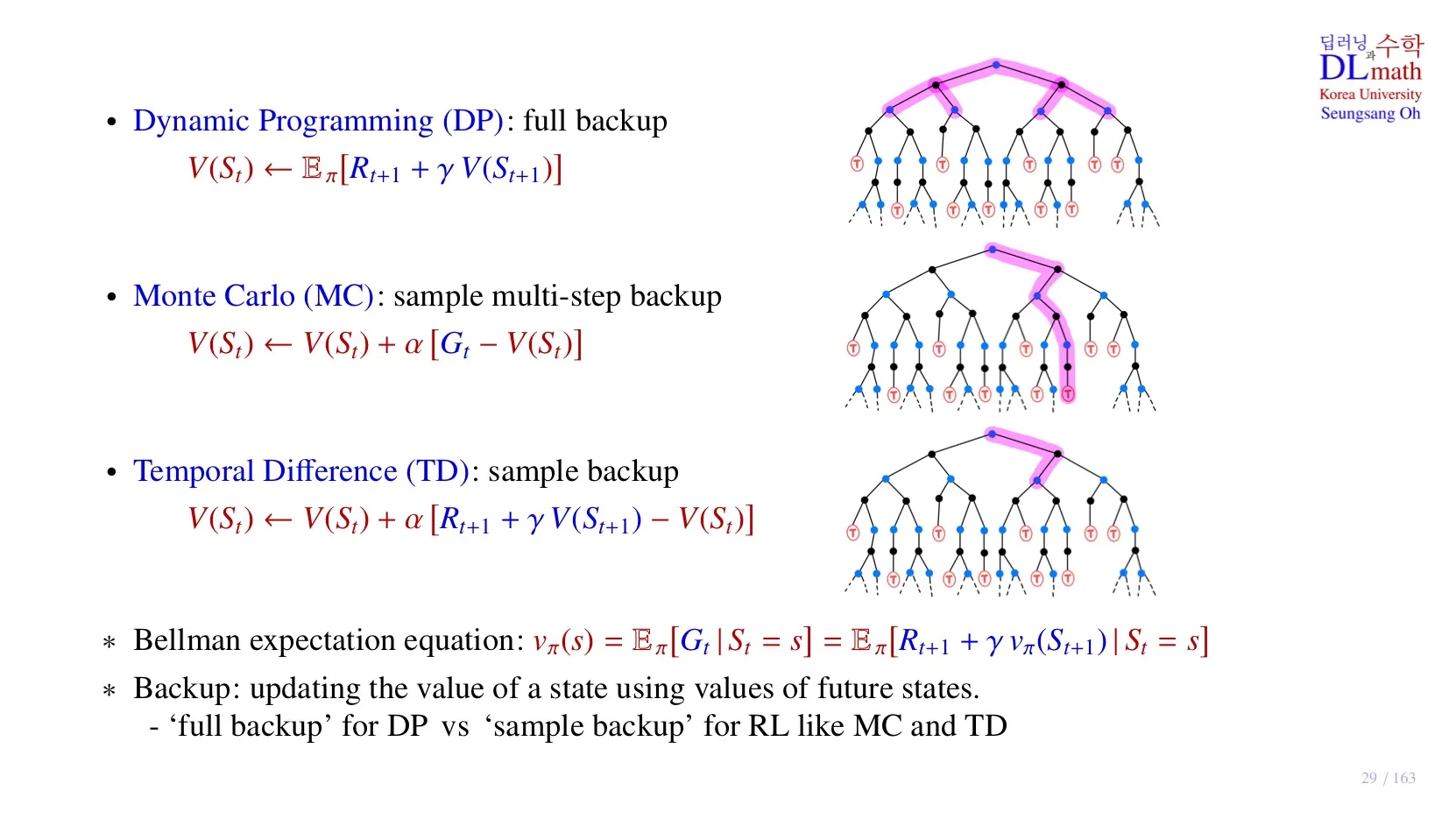
🔷 Dynamic Programming (DP)

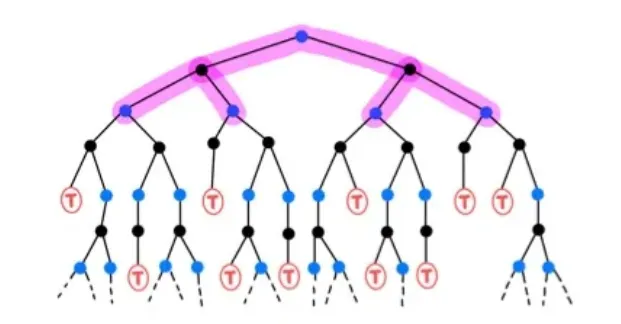
• 현재의 $V(S_t)$를 계산하기 위해 모든 $V(S_{t+1})$를 알아야 한다.
• 모든 미래의 $V(S_{t+1})$를 통해 계산을 수행하기 때문에 full backup이라고 한다.

🔷 Monte Carlo (MC)

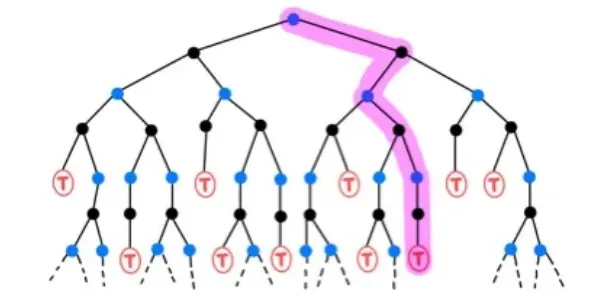
• Sample data를 사용하여 계산한다.
• Return $G_t$를 사용하여 계산한다.
• 하나의 episode의 모든 state를 알아야 하기 때문에 sample multi-step backup이라고 한다.

🔷 Temporal Difference (TD)

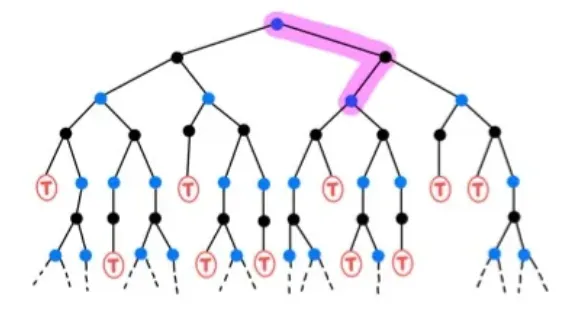
• Sample data를 사용하여 계산한다.
• Immediate Reward $R_{t+1}$와 next state $V(S_{t+1})$를 사용하여 계산한다.
• 다음 state만 알아도 되기 때문에 sample backup이라고 한다.

---

4️⃣ 정리

🔷 7강에서 배운 내용은 아래와 같다.

1. Dynamic programming의 3단계에 대해 배웠다.
2. Dynamic programming을 적용하기 위한 문제 조건에 대해 배웠다.
3. Dynamic prgramming과 Reinforcement Learning의 차이에 대해 배웠다.
4. Reinforcement Learning의 종류에 대해 간단히 살펴보았다.