👨‍🏫학습목표

오늘은 Policy Iteration의 정의와 Value Iteration보다 나은 장점에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=6GhwCE43oFk&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=9

1️⃣ Policy Iteration

📕 지난시간에 배웠던 내용

💡 Value Iteration

Bellman optimality equation을 만족하는 Optimal state value function $V_{\pi}(s)$을 찾는 것이다. 이를 이용하여 Optimal policy $\pi_*$를 찾는다.

😅 Value Iteration의 한계

• 점화식 자체의 연산량이 많다. $O(S^2A)$
• State value function이 수렴하기 전에 Policy가 먼저 수렴하는 경우가 있다. → 필요 이상의 연산량 발생.

❗이러한 한계를 극복하기 위해 등장한 방법이 Policy Iteration이다.

🔷 Policy Iteration

Policy Iteration은 policy evaluation과 policy improvement 이 2단계를 반복적으로 사용하여 진행된다.

🔻 Policy Evaluation (PE): 정책 평가

• Bellman expectation equation을 사용한다.

$v_\pi(s) = \sum_a \pi(a|s) \sum_{s',r} p(s', r | s, a) [r + \gamma v_\pi(s')]$

• Bellman expectation equation을 사용하기 위해서는 Policy가 주어져야 한다.

$a \rightarrow \pi(s) \ ,\ \ \sum_a \pi(a|s) \rightarrow 제거$

• 따라서 $V^\pi$를 Deterministic policy로 두고 시작한다.
  → $\pi(s) = a$ (하나의 state에 하나의 action)

🟤 최종적으로 도출된 점화식

• Policy가 deterministic하기 때문에 action이 모두 고정되어 있다.
• 따라서 Value Iteration과 달리 action에 대한 연산은 수행할 필요가 없다.

$V_{k+1}(s) \leftarrow \sum_{s',r} p(s', r | s, \pi(s))[r + \gamma V_k(s')]$

🟤 수렴 과정

1. Value Iteration과 동일하게 초기 $V_0(s) = 0$으로 설정한다.
2. $V_k(s)$를 통해 $V_{k+1}(s)$를 업데이트 한다.
3. 수렴한 $V^\pi(s)$를 구한다.

여기서 구한 $V^\pi(s)$는 주어진 policy $\pi$에 대한 state value function이다.

🔻 Policy Improvement (PI): 정책 개선

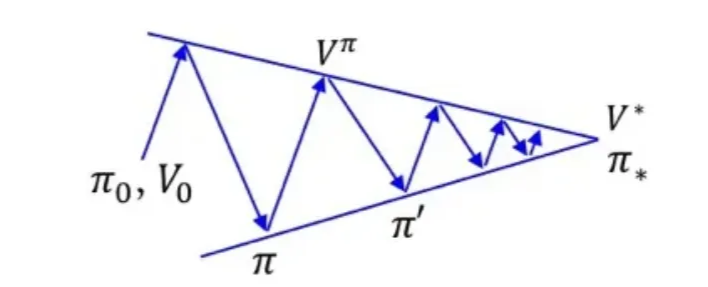
• Policy evaluation을 통해 구한 state value function과 greedy policy를 활용하여 policy를 개선하는 과정이다.

$\pi'(s) = \arg \max_a \sum_{s',r} p(s', r | s, a)[r + \gamma V^\pi(s')]$

• 해당 수식을 통해 개선된 $\pi'(s)$는 optimal은 아니지만, 앞선 policy $\pi$보다는 개선된다는 점이 중요하다.

• Value Interation과 비교하여 훨씬 적은 Iteration으로 optimal policy에 도착한다.

🟤 그렇다면 policy가 개선되는 것은 어떻게 알 수 있을까?

$Q^\pi(s, \pi'(s)) \geq V^\pi(s) = \sum_a \pi(a|s) Q^\pi(s, a)$

• 주어진 policy에서 가능한 모든 action값의 기대값보다 특정 policy $\pi$의 action value가 더 클 수 있다.

• 아래의 식 결과 $\pi$와 $\pi'$는 항상 2가지 경우 중 한가지를 만족한다.
  이를 Policy Improvement Theorm이라 한다.

  • $\pi'$는 $\pi$보다 개선된다.
  • $\pi$와 $\pi'$의 state value function 값이 동일하다.
    (value가 동일한 것이지, policy가 완전히 동일한 것을 의미하지는 않는다.)

---

2️⃣ Policy Improvement Theorem

🔷 Policy Improvement Theorem

$\text{If} \ \ Q^\pi(s, \pi'(s)) \geq V^\pi(s) \text{ for all } s \in \mathcal{S}, V^{\pi'}(s) \geq V^\pi(s) \text{ for all } s \in \mathcal{S}.$

• 수식의 의미: 모든 state에서 $Q^\pi(s, \pi'(s)) \geq V^\pi(s)$ 인 경우, 해당 policy가 개선되었다고 할 수 있다.

🔻 증명

$v_\pi(s) \leq q_\pi(s, \pi'(s))$

• $q_\pi(s, \pi'(s))$을 Bellman equation으로 풀어쓰면

$= \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t=s, A_t=\pi'(s)]$

• 수식을 보면 state-value function은 앞서 구한 policy의 value값을 그대로 사용하는 것을 확인할 수 있다. 그리고 action은 개선된 action을 사용한다. ( $\max\limits_{a}$ 로 결정된 action )

$= \mathbb{E}_{\pi'}[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t=s]$

• 이때 $E$를 계산하기 위해 사용된 확률은 조건부로 $\pi'$이므로 기대값을 $E_{\pi'}$로 바꿀 수 있다.
• 그리고 해당 조건은 생략한다.

$\leq \mathbb{E}_{\pi'}[R_{t+1} + \gamma q_\pi(S_{t+1}, \pi'(S_{t+1})) | S_t=s]$

• $v_\pi(s) \leq q_\pi(s, \pi'(s))$를 사용하여, $\gamma v_\pi(S_{t+1}) \rightarrow \gamma q_\pi(S_{t+1})$로 바꾼다.

$= \mathbb{E}_{\pi'}[R_{t+1} + \gamma \mathbb{E}_{\pi'}[R_{t+2} + \gamma v_\pi(S_{t+2}) | S_{t+1}, A_{t+1}=\pi'(S_{t+1})] | S_t=s]$

• 지금까지의 과정을 반복한다.

$= \mathbb{E}_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2 v_\pi(S_{t+2})] | S_t=s]$

• $E_{\pi'}$를 묶고 조건부 $S_{t+1}, A_{t+1}=\pi'(S_{t+1})$를 제거한다.

$\leq \mathbb{E}_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \dots | S_t=s]$

• $R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \dots \ :$ Return $G_t$ 이므로

$= v_{\pi'}(s)$

• 따라서 주어진 state에 대한 policy $\pi'$의 state-value function이 될 수 있다.

$\text{If} \ \ Q^\pi(s, \pi'(s)) \geq V^\pi(s) \text{ for all } s \in \mathcal{S}, V^{\pi'}(s) \geq V^\pi(s) \text{ for all } s \in \mathcal{S}.$

• 증명 완료, $\max\limits_{a}$ 를 통해 $Q^\pi(s, \pi'(s))$를 구한다.

---

3️⃣ A finite MDP에서 Policy Iteration

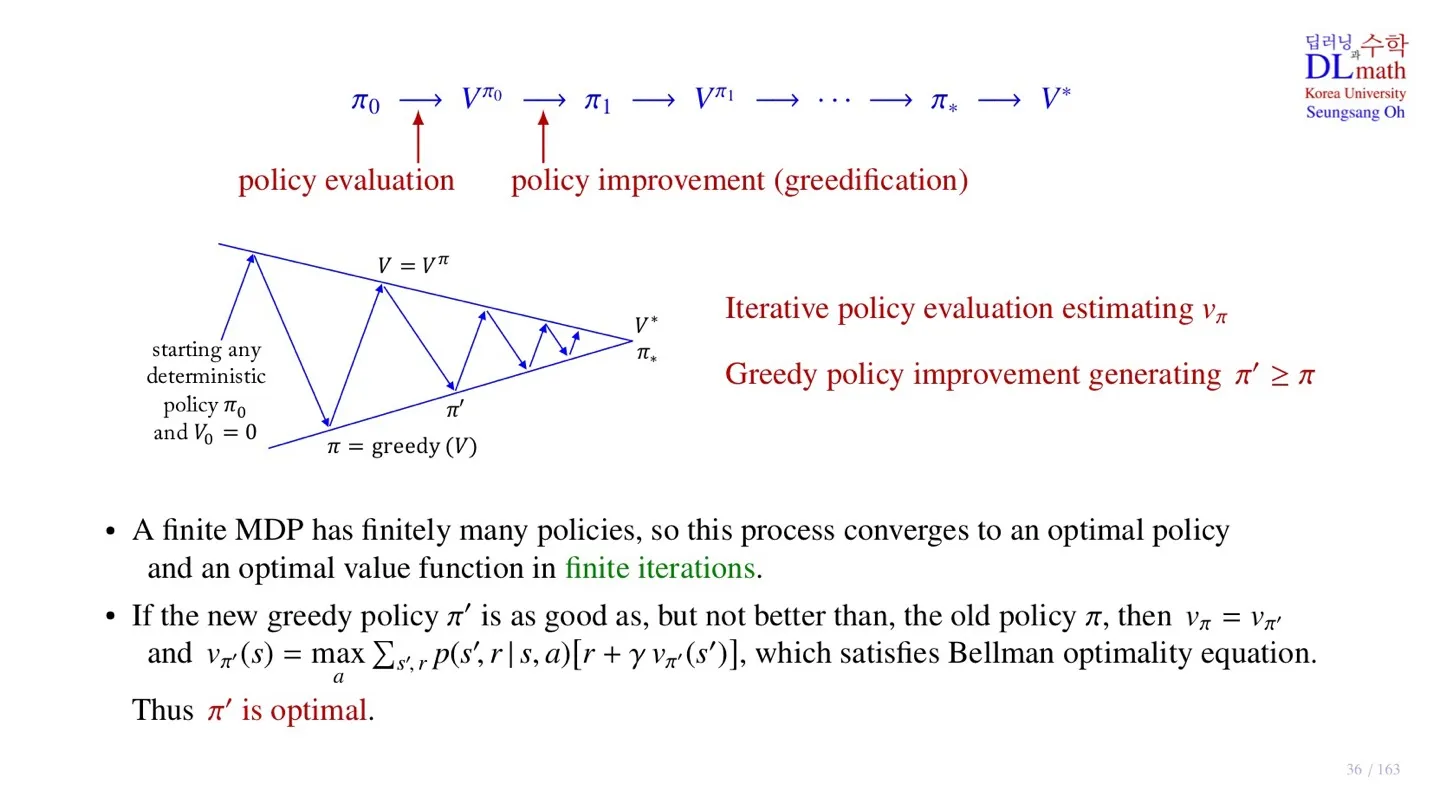
🔷 Iteration

• Policy $\pi_0$를 지정하고 policy evaluation을 통해 state-value function을 구한다.
• Policy improvement를 통해서 새로운 policy $\pi_1$를 구한다.
• 이러한 과정을 수렴할 때까지 반복한다.

🔷 A finite MDP

• A finite MDP는 모델이 취할 수 있는 state와 action이 유한하다는 의미이다. 따라서 모델이 취할 수 있는 policy 역시 유한하다.
• 그 결과 유한한 Iteration을 통해 optimal policy를 구할 수 있다.
• 최종적으로 $\pi = \pi'$을 만족하면

• $\pi'$이 Bellman optimality equation을 만족하는 해가 된다.

---

4️⃣ Policy Iteration의 pseudo code

🔻 1. Initialization

• State-value function $V(s)$와 policy $\pi(s)$ 모두 초기화한다.

🔻 2. Policy Evaluation

• 점화식의 변화, Deterministic policy를 사용하는 것을 제외하고는 Value-Iteration과 동일.

🔻 3. Policy Improvement

• Old policy와 New policy가 다르면 policy Evaluation으로 돌아간다.
• Old policy와 New policy가 동일해질 때까지 진행

---

5️⃣ Convergence of Policy Evaluation

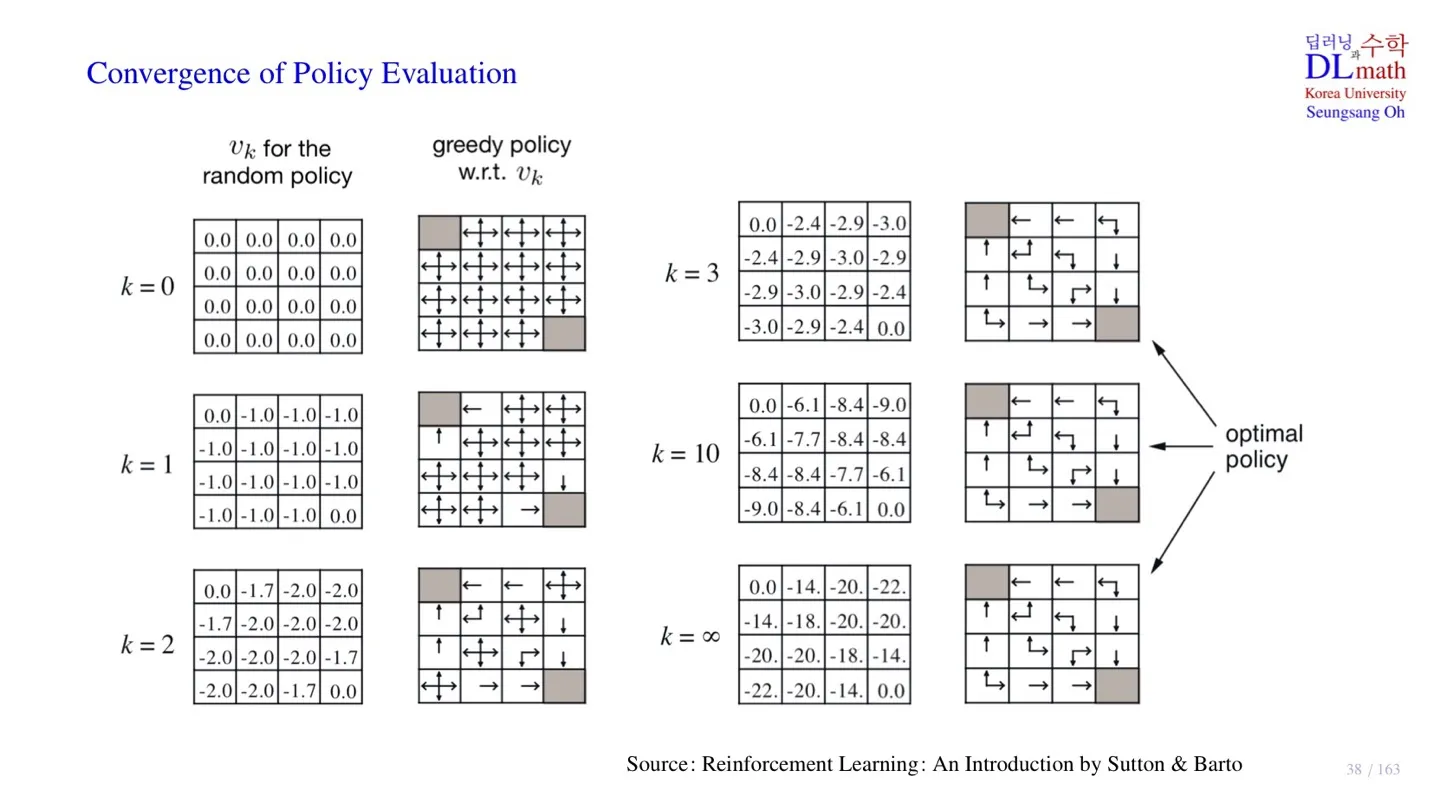
• 주어진 단계에서의 state value function과 improved policy를 확인할 수 있다.
• $k=3$ 이후에는 optimal policy가 고정되어 있는 것을 확인할 수 있다.
• Value Iteration에서는 state-value function이 수렴할 때까지 Iteration이 반복되지만, Policy Iteration을 사용하면 $k=3$에서 Iteration을 멈출 수 있다.

---

6️⃣ Dynamic Programming & Reinforcement Learning

🔷 Dynamic Programming

• Optimal policy를 구하기 위해, Bellman optimality equation을 사용한다.
• 계산을 위해서는 아래의 조건을 필요하다.
  • Markov Property
  • transition probability $p(s',r | s,a)$
  • 각 state-value function값을 저장하기 위한 공간과 시간
• 모든 state-value function값을 저장하기 때문에 몇백만 개 내외의 state에서 구현 가능한다.
• $|\{s\}| \ll |\{(s, a)\}|:$ State와 action을 모두 고려한 $Q(s,a)$를 table에 저장하면 경우의 수가 너무 많아 주로 state-value function을 사용한다.
• state로 표현하는 variable이 너무 많아지면, state의 개수 역시 급격하게 증가하는 문제가 있다.
  • ex) 사족 보행 로봇이 있을 때, 각 다리마다 3개의 관절이 있으면 4개에 총 12개의 관절이 존재한다. 즉 state로 표현 해야하는 variable의 수는 12개이다. 그리고 각 관절이 취할 수 있는 각도 즉 state가 10가지 존재한다고 하자. 그렇다면 사족 보행로봇의 다리의 state는 $10^{12}$가지의 state가 존재한다.
• Robotics의 경우 관절의 수가 굉장히 많기 때문에 Dynamic programming으로 문제를 해결할 수 없다.

🔷 Reinforcement Learning

• 각 Iteration마다 모든 value function이 아닌 일부 value function만 계산한다.
• Value function은 sample 데이터를 통해 얻은 state 또는 state-action pair를 사용한다.
• 완전한 정보로 수행되는 것이 아니기 때문에 Bellman optimality equation의 근사치를 사용한다.
• Sampling을 사용하기 때문에 Curse of dimension에서 자유롭다.
• 컴퓨팅 비용은 학습 시 사용하는 Batch의 개수에 결정되어 state의 개수와는 무관한다.

---

7️⃣ 정리

🔷 9강에서 배운 내용은 아래와 같다.

1. Policy Iteration의 2단계에 대해 배웠다.
2. Policy Improvement Theorem에 대해 증명하였다.
3. Policy Iteration의 pseudo code에 대해 살펴보았다.
4. Value Iteration보다 연산량이 적음을 배웠다.
5. 연산량의 관점에서 Dynamic Programming과 Reinforcement Learning을 비교하였다.