📖 시계열 분석을 하는데 있어 기본적인 요소들을 공부해봅시다.
시계열 분석 절차

시계열 데이터의 다양한 형태
par(mfrow=c(2,3))
options(family="NanumGothic")
# 백색잡음 시계열 -----------------------------------------------------------
y_t <- rnorm(100, mean=0, sd=1)
ts.plot(y_t, main="백색잡음(White Noise)",xlab="시간(time)", col="blue", lwd=2)
abline(h=0)
# 추세를 갖는 시계열--------------------------------------------------
e <- rnorm(100, 0, 10)
trend_yt <- 0.5*seq(1,100) + e
ts.plot(trend_yt, lwd=2, col="blue", main="추세를 갖는 시계열")
abline(a=0, b=0.5)
# 랜덤워크 시계열 -----------------------------------------------------------
e <- rnorm(100)
rw_yt <- cumsum(e)
ts.plot(rw_yt, lwd=2, col="blue", main="랜덤워크 시계열")
abline(h=0)
# 분산이 커지는 시계열 -----------------------------------------------------------
e <- sapply(1:100, function(x) rnorm(1, sd = 2*x/100))
var_yt <- 0.1*seq(1,100) + e
ts.plot(var_yt, lwd=2, col="blue", main="추세와 분산이 커지는 시계열")
abline(a=0, b=0.1)
# 평균이 증가하는 시계열 -----------------------------------------------------------
mean_yt <- c(rnorm(50), rnorm(50, 5))
ts.plot(mean_yt, lwd=2, col="blue", main="평균이 변화하는 시계열")
abline(a=0, b=0)
abline(a=5, b=0)
# 분산이 변화하는 시계열 -----------------------------------------------------------
var_change_yt <- c(rnorm(150,0,1), rnorm(200,0,10), rnorm(150,0,1))
ts.plot(var_change_yt, lwd=2, col="blue", main="분산이 변화하는 시계열")
abline(a=0, b=0) 
정상성(Stationarity) 확보
정상성
- 정상성을 갖는 시계열 데이터는 특성이 시간의 흐름에 따라 변하지 않음을 의미합니다.
- 즉 시간에 따라 일정한 평균, 분산, 공분산을 갖습니다.
- 추세나 계절성이 있는 시계열은 정상 시계열에서 벗어납니다.
- 다음 세 가지 조건을 충족하면 됩니다.

# 기본적으로 시계열 모형은 시계열 데이터의 정상성을 가정하기에, 정상성을 확보하는 것이 중요합니다. 정상성을 갖지 않는 시계열 데이터를 정상 시계열로 돌리는데 다음과 같은 기법이 동원됩니다.
1) 로그변환: log(Yt) 을 통해 분산이 커지는 경향(혹은 변동폭이 일정하지 않는 경향)을 갖는 시계열을 안정화 시킴.
2) 차분: diff(Yt) 을 통해 차분을 하계 되면 추세를 제거하는 효과를 거둠.
3) 계절차분: diff(Yt,s) 을 통해 계절 차분을 하계 되면 계절추세를 제거하는 효과를 거둠.
백색잡음(White Noise)
- 백색잡음은 고정된 평균, 분산을 갖고 시계열 상관이 없는 시계열 데이터로 arima.sim() 함수를 통해 모수를 조절해서 백색잡음 시계열로 추출할 수 있습니다.
white_noise_zero <- arima.sim(model = list(order = c(0, 0, 0)), n = 250)
white_noise_mean_sd <- arima.sim(model = list(order = c(0, 0, 0)), n = 250, mean =5, sd =2)
par(mfrow=c(1,2))
ts.plot(white_noise_zero, ylim=c(-10,10))
ts.plot(white_noise_mean_sd, ylim=c(-10,10))
시계열 분해법
- 시계열 데이터를
추세/순환/계절/불규칙요소로 분해하는 기법입니다.
1) 추세성(Tt)
- 데이터가 장기적으로 증가하거나 감소하는 것, 추세가 꼭 선형적일 필요가 없음.
2) 순환성(Ct)
- 경기변동과 같이 정치, 경제, 사회적 요인에 의한 변화로, 일정 주기가 없으며 장기적인 변화 현상.
3) 계절성(St)
- 주, 월, 분기, 반기 단위 등 특정 시간의 주기로 나타나는 패턴.
4) 불규칙성(It)
- 설명될 수 없는 요인 또는 돌발적인 요인에 의하여 일어나는 변화로, 예측 불가능한 임의의 변동.
1. 가법 모형(additive model)
- 모형 식은 다음과 같습니다.
yt=Tt+Ct+St+It
beer <- window(fpp2::ausbeer,start=1992,end=c(2007,4)) #data
par(mfrow = c(2,2))
decompose_beer <- decompose(beer, "additive")
plot(beer, main = '원 데이터')
plot(decompose_beer$seasonal, main = '계절성')
plot(decompose_beer$trend, main = '추세성')
plot(decompose_beer$random, main = '불규칙성')
2. 승법 모형(multiplicative model)
- 모형 식은 다음과 같습니다.
yt=Tt×Ct×St×It
par(mfrow = c(2,2))
decompose_beer <- decompose(beer, "multiplicative")
plot(beer, main = '원 데이터')
plot(decompose_beer$seasonal, main = '계절성')
plot(decompose_beer$trend, main = '추세성')
plot(decompose_beer$random, main = '불규칙성')
3. STL
-
STL은 다양한 상황에서 사용할 수 있는 강력한 시계열 분해 기법입니다. STL은 “Seasonal and Trend decomposition using Loess(Loess를 사용한 계절성과 추세 분해)”의 약자입니다. 여기에서 Loess는 비선형 관계를 추정하기 위한 기법입니다.
-
장점
1) SEAT와 X11과는 다르게, STL은 월별이나 분기별 데이터를 포함하여 어떤 종류의 계절성도 다룰 수 있습니다.
2) 계절적인 성분이 시간에 따라 변해도 괜찮습니다. 계절성분의 변화율을 사용자가 조절할 수 있습니다.
3) 추세-주기의 매끄러운 정도를 사용자가 조절할 수 있습니다.
4) 가끔 있는 이상값이 추세-주기와 계절성분에 영향을 주지 않게 만들 수 있습니다. 하지만 이상값은 나머지 성분(remainder)에 영향을 줄 것입니다.
window(fpp2::ausbeer,start=1992,end=c(2007,4)) %>%
stl(t.window=13, s.window="periodic", robust=TRUE) %>%
autoplot()
# t.window : 추세-주기를 추정할 때 사용할 연이은 관측값의 개수
# s.window : 계절성분에서 각 값을 추정할 때 연이은 관측값의 개수
# 위 두 매개변수 모두 값이 홀수이어야하며, 값이 작을수록 더 급격하게 변합니다.

# s.window 매개변수 조정은 계절의 패턴이 시간에 따라 일정하다고 판단되면 "periodic" 혹은 큰 수를, 계절의 패턴이 시간의 흐름에 따라 진화한다고 판단되면 최근 데이터만 사용할 수 있도록 작은 수를 입력합니다.
시차 그래프
- 분기별로 호주 맥주 생산량의 산점도를 나타냅니다.
- 가로축은 시계열의 시차값(lagged value)을 나타냅니다.
- 각 그래프는 서로 다른 k값에 대해서 yt(세로축)를 yt-k(가로축)에 대해 나타낸 것입니다.
gglagplot(beer) +
guides(colour=guide_legend(title="분기")) +
ggtitle("")
해석
- 시차 4와 시차 8에서 양의 관계가 뚜렷합니다. 이는 데이터에 계절성이 강하게 있다는 것을 반영합니다.
- 시차 2와 시차 6에서 음의 관계가 나타납니다.
자기상관함수(ACF)
- 상관값이 두 변수 사이의 선형 관계의 크기를 측정하는 것처럼, 자기상관은 시계열의 시차 값 사이의 선형 관계를 측정합니다.
- 시차가 커질수록 ACF는 0에 가까워집니다.
- 정상 시계열은 상대적으로 빠르게 0에 수렴하며, 비정상 시계열은 천천히 감소하고, 종종 큰 양의 값을 가집니다.
- Yt와 Yt+k사이의 자기상관을 구하는 식은 다음과 같습니다.
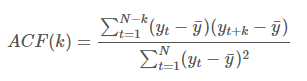
- 다음의 표는 맥주 생산량 데이터에 대한 처음 9개의 자기상관계수를 보여줍니다.

- 이 값은 위 시차 그래프와 대응됩니다. 자기상관계수는 보통 자기상관함수(ACF)를 나타내기 위해 그립니다. 이 그래프는 상관도표라고도 알려져 있습니다.
ggAcf(beer)
해석
- r4는 다른 시차들의 경우보다 값이 높은데, 이 것은 데이터의 계절성 패턴때문입니다. 고점은 4개의 분기마다 나타나는 경향이 있고, 마찬가지로 저점 역시 4개의 분기마다 나타나는 경향이 있습니다.
- r2는 다른 시차들보다 더 큰 음의 값을 나타내는데, 왜냐하면 저점이 고점 직후의 2개 분기마다 나타나는 경향 때문입니다.
- 파란 점선은 상관계수가 0과 유의하게 다른지 아닌지를 나타냅니다. 저 안에 들어야 정상성을 띄운다고 할 수 있습니다. (= 백색잡음)
편자기상관함수(PACF)
- 편자기상관계수는 자기상관성을 파악하되, Yt와 Yt−k사이에 있는 Yt−1,⋯,Yt−(k−1)의 영향을 제거하고 딱 둘 사이의 관계를 파악하려고 하는 것입니다.
- 예를 들어, X1, X2, X3 변수가 변수 Y를 회귀하는 경우, Y와 X3간의 부분상관은 X1, X2와의 공통 상관으로 설명되지 않는 상관관계의 양을 의미합니다.
- 첫 번째 부분 자기상관은 제거할 부분이 없어서 첫 번째 자기상관과 같습니다.
- 부분 자기상관값은 보통의 자기상관값처럼 ±1.96/√T로 같은 임계 값을 갖습니다.
- Yt와 Yt+k사이의 편자기상관을 구하는 식은 다음과 같습니다.
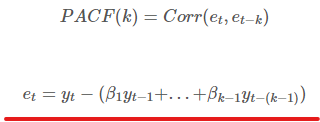
ggPacf(beer)
단순 예측 기법
1. 평균 기법
- 미래 모든 값은 과거 데이터의 평균.
2. 단순 기법
- 모든 예측값을 단순하게 마지막으로 둠.
3. 계절성 단순 기법
- 각 예측값을 연도의 같은 계절의 마지막 관측값으로 둠.
4. 표류(diff) 기법
- 시간에 따른 변화량을 과거 데이터에 나타나는 평균 변화량으로 정함.
# 위 4가지 기법 시각화-------------------------------------
ggplot2::autoplot(beer) +
autolayer(meanf(beer, h=5),
series="평균", PI=FALSE) +
autolayer(naive(beer, h=5),
series="단순", PI=FALSE) +
autolayer(snaive(beer, h=5),
series="계절성 단순", PI=FALSE) +
autolayer(rwf(beer, h=5, drift = TRUE),
series="표류", PI=FALSE) +
labs(title = '분기별 맥주 생산량 예측값',
x = '연도', y = '단위:백만 리터') +
guides(color = guide_legend(title = '예측'))
ARIMA 모델
1. ARIMA 구성
- AR 모형
- 자기상관성을 시계열 모형으로 구성하였으며, 예측하고자 하는 특정 변수의 과거 관측값의 선형결합으로 해당 변수의 미래값을 예측하는 모형입니다.
- 이전 자신의 관측값이 이후 자신의 관측값에 영향을 준다는 아이디어에 기반하였습니다.
- AR(p)모형의 식은 다음과 같습니다.
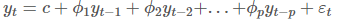
- 여기에서 c는 상수(절편), ϕ는 가중치, εt 는 백색잡음(white noise)입니다. yt의 시차 값을 예측변수(predictor)로 다루는 것만 제외하면 다중 회귀처럼 생겼습니다. 이것을 p 자기회귀 모델인 AR(p) 모델이라고 부르겠습니다.
- AR(1) 모델은 :
1) ϕ1=0일 때, yt는 백색잡음과 같습니다.
2) ϕ1=1이고 c=0일 때, yt 는 확률보행(랜덤워크) 모델과 같습니다.
3) ϕ1=1 이고 c≠0일 때, yt는 표류가 있는 확률보행 모델과 같습니다.
4) ϕ1<0일 때, yt는 평균값을 중심으로 진동하는 경향을 나타냅니다. - 보통 자기회귀 모델을 정상성을 나타내는 데이터에만 사용합니다.
- MA 모형
- 회귀에서 목표 예상 변수(forecast variable)의 과거 값을 이용하는 대신에, 이동 평균 모델은 회귀처럼 보이는 모델에서 과거 예측 오차(forecast error)을 이용합니다.
- MA(q)모형의 식은 다음과 같습니다.
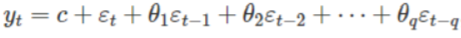
ARIMA는 위의 AR(AUtoregression)모형과 MA(Moving Average)모형을 합친 모형으로, 식은 다음과 같습니다.
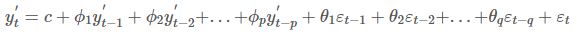
- ACF와 PACF를 동시에 고려하여 ARIMA 모델의 p와 q를 결정합니다. 그 방법은 다음과 같습니다.

2. ARIMA 모델을 활용한 예측 실습
1. Augmented Dickey Fuller 검정
- 시계열 데이터의 정상성 확인을 위해 adf.test를 실시합니다.
beer <- window(fpp2::ausbeer,start=1992,end=c(2007,4))
# 원 데이터는 2010 2분기까지 존재
tseries::adf.test(beer) #단위근 검정
## 귀무가설(H0): 자료에 단위근이 존재한다.
## 대립가설(H1): 자료에 단위근이 존재하지 않아 시계열 자료가 정상성을 만족한다.> tseries::adf.test(beer)
Augmented Dickey-Fuller Test
data: beer
Dickey-Fuller = -3.8813, Lag order = 3, p-value = 0.02061
alternative hypothesis: stationary해석
- 유의수준 0.05이하로 위 데이터는 정상성을 만족합니다.
비정상 시계열 데이터일 경우, 시계열 분해법을 이용해 4가지 요인으로 분해하여 데이터를 파악하여 로그변환, 일반차분, 계절차분을 이용해 정상 시계열 데이터로 변환해줍니다.
2. ACF & PACF 확인
- 위 검정에선 데이터가 정상성을 띄운다고 하였으나, 원 데이터에 대한 ACF그래프를 보아, 계절성을 띄우고 있는 것이 확인되기에 계절 차분이 필요하다고 판단이 됩니다.
TIP
ndiffs(데이터) : 몇 번의 차분을 해야할지 정해준다.
nsdiffs(데이터) : 몇 번의 계절 차분을 해야할지 정해준다.
p와 q를 정하는 방법
- lag(x좌표) =0 인 지점은 읽지 않고 어느 지점 부터 구간안에 들어가는지를 파악하면 됩니다. 예를 들어 ACF가 lag=2에서 절단점을 가지고(절단점-1= 1 = q), PACF는 lag=2(절단점 -1 = p=1)이후에 절단점을 가집니다. (일반적으로 p,q < 3)
3. ARIMA 분석 및 잔차 진단(모형 진단)
- 자동으로 ARIMA 모델을 정해주는
auto.arima함수를 활용하여 여러 모델의 AICc를 확인하고 가장 낮은 AIC를 가진 모델을 채택하도록 하겠습니다.
auto_arima_beer <- auto.arima(beer, trace=TRUE, test="adf", ic="aicc")
summary(auto_arima_beer)
checkresiduals(auto_arima_beer) # 잔차 진단
#Ljung-BOX test까지 해줘요!> auto_arima_beer <- auto.arima(beer, trace=TRUE, test="adf", ic="aicc")
ARIMA(2,0,2)(1,1,1)[4] with drift : Inf
ARIMA(0,0,0)(0,1,0)[4] with drift : 511.942
ARIMA(1,0,0)(1,1,0)[4] with drift : 490.9862
ARIMA(0,0,1)(0,1,1)[4] with drift : 481.6034
ARIMA(0,0,0)(0,1,0)[4] : 510.7779
ARIMA(0,0,1)(0,1,0)[4] with drift : 508.715
ARIMA(0,0,1)(1,1,1)[4] with drift : 482.738
ARIMA(0,0,1)(0,1,2)[4] with drift : 482.4688
ARIMA(0,0,1)(1,1,0)[4] with drift : 490.5411
ARIMA(0,0,1)(1,1,2)[4] with drift : 484.9341
ARIMA(0,0,0)(0,1,1)[4] with drift : 483.4529
ARIMA(1,0,1)(0,1,1)[4] with drift : 483.9154
ARIMA(0,0,2)(0,1,1)[4] with drift : 483.822
ARIMA(1,0,0)(0,1,1)[4] with drift : 481.7344
ARIMA(1,0,2)(0,1,1)[4] with drift : 486.2001
ARIMA(0,0,1)(0,1,1)[4] : 488.6937
Best model: ARIMA(0,0,1)(0,1,1)[4] with drift
> summary(auto_arima_beer)
Series: beer
ARIMA(0,0,1)(0,1,1)[4] with drift
Coefficients:
ma1 sma1 drift
-0.2593 -0.7313 -0.3983
s.e. 0.1208 0.0938 0.0991
sigma^2 estimated as 154.9: log likelihood=-236.44
AIC=480.88 AICc=481.6 BIC=489.25
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set -0.4749186 11.7439 8.735055 -0.1229367 2.011984 0.610843
ACF1
Training set -0.01387772
> checkresiduals(auto_arima_beer)
Ljung-Box test
data: Residuals from ARIMA(0,0,1)(0,1,1)[4] with drift
Q* = 2.787, df = 5, p-value = 0.7328
Model df: 3. Total lags used: 8
Ljung-BOX(융 박스 검정) 해석
- 귀무가설 : 잔차 간 자기상관성이 없다.
- 유의수준 0.05보다 크므로 잔차가 정상시계열을 만족한다는 것입니다.
잔차 진단 그림 해석

- 잔차의 ACF 확인 결과, 잔차 간 자기상관성이 없는 것을 확인할 수 있습니다..
- 잔차의 분포를 보아하니 정규분포를 따른다고 알 수 있습니다.
- 잔차 진단 결과, 해당 모형은 정상성, 정규성, 등분산성을 모두 만족하는 것으로 보아 아주 좋은 모형이라는 것을 알 수 있습니다.
4. 예측값 확인 및 시각화
fore_model1 <- forecast(auto_arima_beer, h = 10)
fore_model1
autoplot(fore_model1, lwd = 5) + autolayer(fore_model1$fitted) +
autolayer(window(fpp2::ausbeer,start=c(2008,1),end=c(2010,2)))> fore_model1
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
2008 Q1 427.6151 411.6671 443.5631 403.2248 452.0054
2008 Q2 383.9695 367.4939 400.4450 358.7723 409.1666
2008 Q3 399.9629 383.4874 416.4385 374.7658 425.1601
2008 Q4 478.5510 462.0755 495.0266 453.3539 503.7482
2009 Q1 423.6286 406.6047 440.6524 397.5929 449.6642
2009 Q2 382.3762 365.3161 399.4362 356.2850 408.4673
2009 Q3 398.3696 381.3096 415.4297 372.2785 424.4608
2009 Q4 476.9577 459.8977 494.0178 450.8666 503.0489
2010 Q1 422.0353 404.4451 439.6254 395.1334 448.9371
2010 Q2 380.7829 363.1576 398.4081 353.8274 407.7383

