행렬

행렬 (Matrix)

• 단순 정의 : 사각형 안에 수를 행과 열에 맞춰 배열한 것

  • 복잡한 선형 변환의 식을 계산하기 편하게 단순화시킨 계산 도구

  • 선형 변환의 표현

• 함수로서의 행렬 : $2\times 2 Matrix$

• 벡터로서의 행렬 : $2\times 1 Matrix$

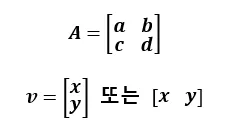
행렬과 행렬의 덧셈 연산

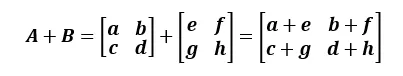
행렬과 스칼라의 곱셈 연산

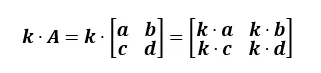
행렬의 전치 (Transpose) 연산

• 행과 열을 변경

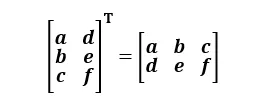
행렬과 행렬의 곱셈 연산

• 행과 열을 교차해서 곱해준 후 더함

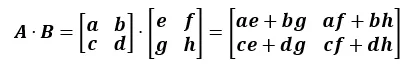
행렬 곱셈 연산의 특징

• 교환 법칙을 만족하지 않음

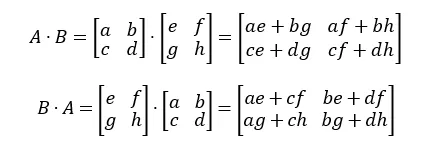
• 결합 법칙은 만족

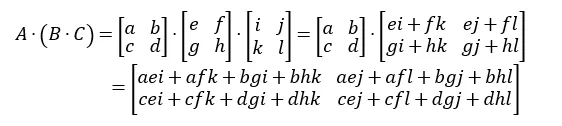
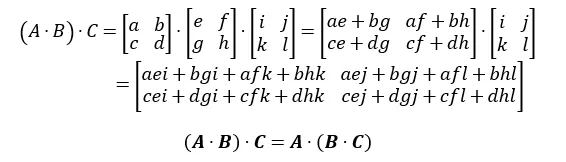
• 행렬 곱의 전치 연산

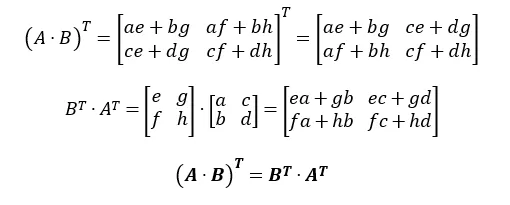
• 복잡하지만 분배법칙도 만족

선형 변환과 행렬

• $\mathbb{R}^2 \mapsto \mathbb{R}^2$ 대응관계를 가지는 선형 변환의 식

• 정방행렬과 열벡터의 곱셈

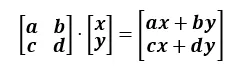
• 이의 결과는 무엇을 의미하는가?

  • 정방 행렬은 같은 차원의 공간이 서로 대응되는 선형 변환을 의미한다.

  • 열벡터는 벡터 공간의 벡터를 의미한다

열기반 행렬과 행기반 행렬

• 열기반(Column Major) Matrix : OpenGL → 수학에서 사용하는 기본 방식

• 행기반(Row Major) Matrix : DirectX 및 게임 엔진에서 사용하는 방식

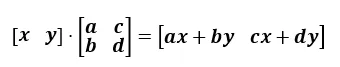
• 열기반과 행기반은 전치 관계일 뿐 결과는 동일함을 보장

선현 변환의 시각화

원 벡터 공간의 선형 변환

• 원 공간에 속한 임의의 벡터에 대한 조합식

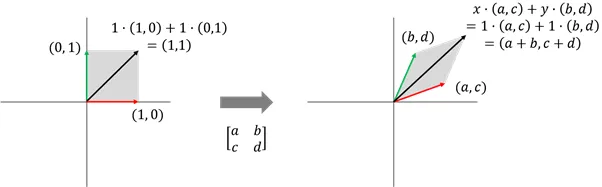
• 선형 변환 후 변환된 기저 벡터를 조합해 벡터를 추적

기저 벡터의 변환

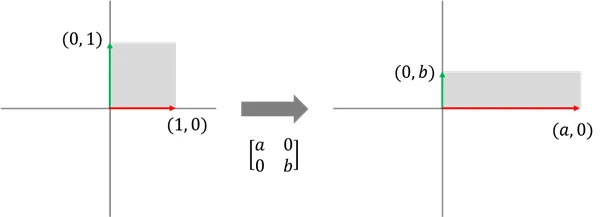
크기 변환 행렬

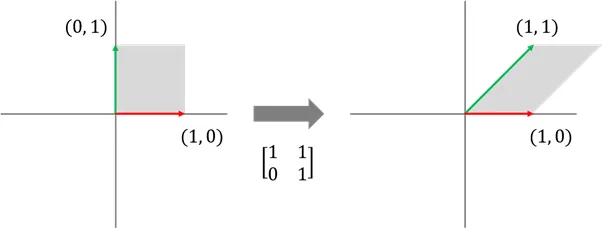
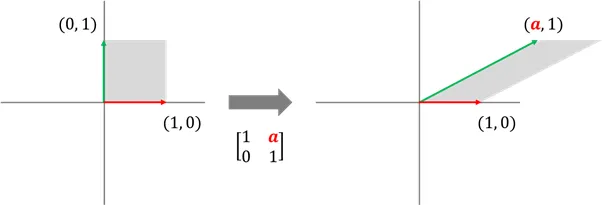
밀기 변환

시계 방향 90도 회전 변환

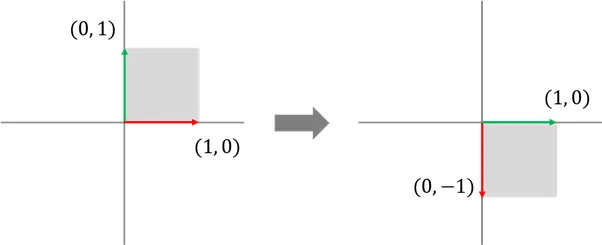
반시계 방향 90도 회전 변환

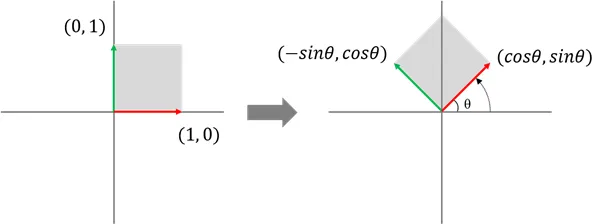
임의의 각 $\theta$에 대한 회전 변환

4. 행렬의 곱

행렬의 곱

• 행렬은 하나의 선형 변환에 대응되며 행렬의 곱은 선형 변환을 적용한 결과에 다시 선형 변환을 적용한 결과를 다음과 같이 진행

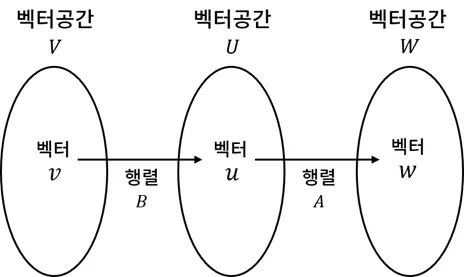
• 이를 수식으로 나타내면

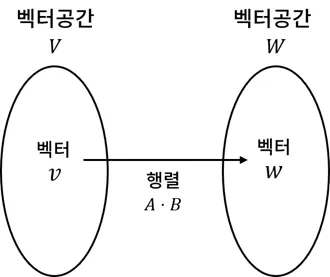
• 그런데 행렬은 결합법칙이 성립하므로 위 식은 다음과 동일

• 그렇다면 두 행렬을 곱한 식 $(A\cdot B)$는 벡터공간 $V$에서 벡터공간 $W$로 직행하는 합성변환을 의미하며 함수의 $A\circ B$와 동일한 의미를 갖음

삼각함수의 합 공식

• 이러한 행렬의 특징을 사용하면 삼각함수의 합 공식을 유도 가능

행렬의 장점

• 이러한 결합법칙이 성립하는 행렬 연산의 특징은 변환이 여러 개가 존재하더라도 동일한 결과를 보장

• 앞으로 우리가 사용할 주요 선형 변환은 다음과 같음

  • Scale ( S )
  • Rotation ( R )
  • Translation ( T )
  • View ( V )
  • Projection ( P )

• 10만개의 벡터에 위의 다섯가지 변환을 각각 적용하면 다음과 같이 50만번의 연산이 발생

• 그런데 변환이 고정되어 있다면 $PVTRS$를 미리 계산해 행렬을 생성한 후 이를 사용하면 동일한 결과를 만들어주는 연산은 10만번으로 해결