벡터의 내적 (Dot Product)
- 벡터의 연산
- 기본 연산이란?
- 유용한 연산의 종류
- 벡터와 벡터의 곱 (a,b,c)⋅(d,e,f)=(ad,be,cf)
- 벡터의 내적
- 벡터의 외적 (3차원에서만 성립)
벡터의 내적 (Dot Product)
(a,b)⋅(c,d)=ac+bd
-
벡터 내적의 성질
- 교환 법칙 : u⋅v=v⋅u
(a,b)⋅(c,d)=ac+bd(c,d)⋅(a,b)=ca+db∴(a,b)⋅(c,d)=(c,d)⋅(a,b)
- 결합 법칙 : (u⋅v)⋅w=u⋅(v⋅w)
- 분배 법칙 : u⋅(v+w)=u⋅v+u⋅w
-
유용한 벡터 내적의 식
(u+v)⋅(u+v)=u⋅u+v⋅v+2(u⋅v)(x,y)⋅(x,y)=x2+y2(u+v)⋅(u+v)=u⋅u+v⋅v+2(u⋅v)=∣u∣2+∣v∣2+2(u⋅v)
-
v=(x,y) 의 크기는 ∣v∣=x2+y2 노름(Norm)
-
v⋅v=∣v∣2
벡터 내적의 코사인 공식
a⋅b=∣a∣∣b∣cosθ
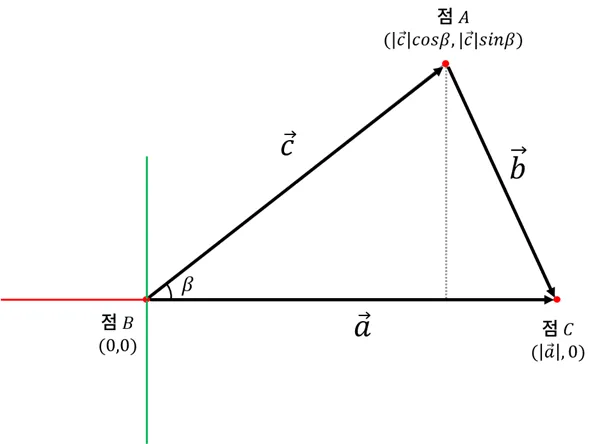
- 점 B를 원점에 두고 변을 벡터로 설정할 때 각 점의 위치
B=(0,0)C=(∣a∣,0)A=(∣c∣cosβ,∣c∣sinβ)
b=(C−A)=(∣a∣−∣c∣cosβ,∣c∣sinβ)
- 벡터 b의 크기를 제곱한 결과는 벡터를 내적한 결과와 동일
∣b∣2=(∣a∣−∣c∣cosβ)2+∣c∣sinβ2=∣a∣2−2∣a∣∣c∣cosβ+∣c∣cosβ2+∣c∣sinβ2=∣a∣2+∣c∣2−2∣a∣∣c∣cosβ=b⋅b
- 벡터 b를 벡터 a,c로 바꾸어 표현
b⋅b=(a−c)⋅(a−c)=(a+(−c))⋅(a+(−c))=∣a∣2+∣c∣2−2a⋅c
−2∣a∣∣c∣cosβ=−2a⋅c∴a⋅c=∣a∣∣c∣cosβ
a⋅b=cosθ
벡터 내적의 직교성 판별
- 벡터의 크기가 0이 아닐 때 내적이 0이 나오는 경우는 코사인 함수가 0 일 때
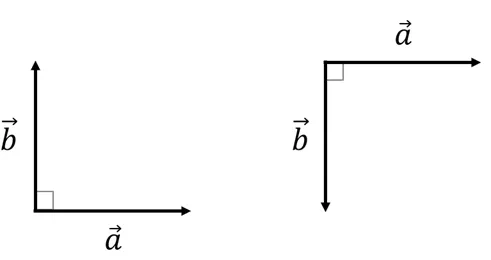
-
이는 두 벡터가 서로 직각을 이룰 때만 성립
-
이러한 두 벡터가 90° 를 이루고 있는 성질을 직교성
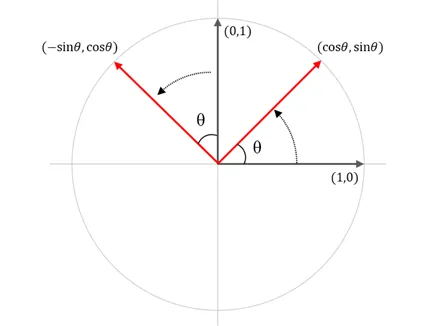
-
(cosθ,sinθ)
-
(−sinθ,cosθ)
-
두 벡터가 직교한다는 것을 직접 그림으로 확인하지 않아도 내적으로 증명 가능
(cosθ,sinθ)⋅(−sinθ,cosθ)=0
- 물체의 형태가 변하지 않는 변환의 조건은 무엇인가?
- 공간을 구성하는 모든 기저 벡터의 크기가 1
- 모든 기저 벡터가 서로 직교하고 있어야 함
- 선형 변환의 행렬식 값이 1
- 이를 만족하는 변환은 회전 변환
[cosθsinθ−sinθcosθ]
- 따라서 회전 변환은 물체의 형태를 변형시키지 않음
벡터 내적의 활용
앞뒤 판별
- 벡터 내적의 코사인 공식을 활용해 목표물이 앞에 있는지 뒤에 있는지 파악 가능
- 사잇각이 (−90°,90°) 범위에 있으면 앞에 있음을 의미하고 코사인 함수는 해당 범위에서 항상 양의 값을 가짐
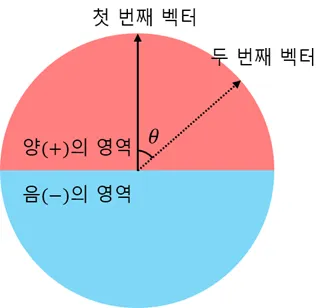
- 두 벡터를 내적한 결과 값이 양수면 앞에 있고, 음수면 뒤에 있음을 바로 파악이 가능
시야 판별
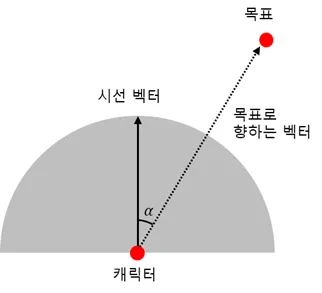
- 캐릭터에 시야각을 설정하고 목표물이 시야각 내에 있는지 확인
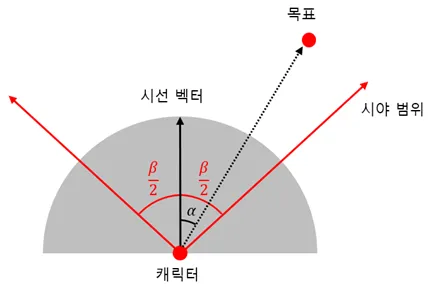
각 α가 시야각의 절반 값 2β 보다 작다면 목표물은 시야각 내에 위치한다고 볼 수 있다.
그렇다면 이를 어떻게 파악할 수 있을까?
- cos2β 값을 미리 구해 저장
- 시선벡터와 목표물로 향하는 벡터의 크기를 1로 조정한다. 그렇다면 두 벡터의 내적은 cosα
- 코사인 함수는 (0°,180°) 범위에서 각이 증가할수록 값이 감소
- 따라서 두 코사인 함수 값을 비교해 cosα 값이 더 크면 시야범위 내에 있다고 파악
음영 계산
- 램버트 코사인 법칙 : 물체 표면이 반사하는 빛의 휘도(Luminance)는 표면 방향과 광원 방향의 사잇각의 코사인 값에 비례
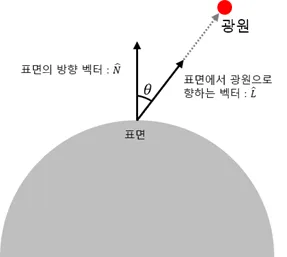
- 이 공식은 셰이더 조명 공식의 가장 기본 식이며 흔히 N⋅L로 불림
투영 벡터 공식
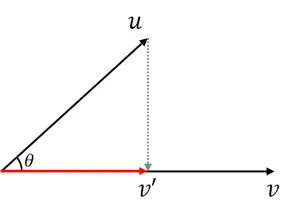
- 벡터 u의 투영 벡터 벡터 벡터 v′와 v 는 크기만 다를 뿐 같은 방향을 가짐
![업로드중..]()
- 벡터 v^는 다음과 같이 구할 수 있음
v^=∣v∣v
- 벡터 v′의 크기는 코사인 함수를 사용해 구할 수 있음
∣v′∣=∣u∣cosθ
- 이를 위해서는 사잇각 θ를 알아야 한다. 이는 내적으로 구할 수 있음
u⋅v=∣u∣∣v∣cosθ∴cosθ=∣u∣∣v∣u⋅v
- 이를 대입하면 투영 벡터의 최종 식을 구할 수 있음
v′=∣v∣2(u⋅v)⋅v=(v⋅v)(u⋅v)⋅v
여기서 투영 하려는 벡터의 크기가 1이라면 이 식은 다음과 같이 단순해짐
v′=(u⋅v)⋅v