직선

아핀 공간에서 점의 조합

• 앞서서 아핀 공간에서 점 + 점의 연산은 불가능 하였음

• 스칼라 보조를 사용하여 다음과 같은 조합식을 만들 때

• 2차원의 점이라고 가정할 경우 위 조합식은 다음과 같이 전개됨

• 이 때 위 결과가 점이 되기 위해서는 마지막 차원 값이 반드시 1이 되어야 한다. 따라서 다음의 수식이 성립

• 이를 원 식에 대입하면 다음의 식이 만들어지며 이는 점을 보장해주며 $a$값에 따라 무수히 많은 점을 만들어낼 수 있음

아핀 조합의 수식

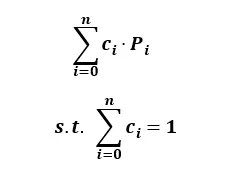
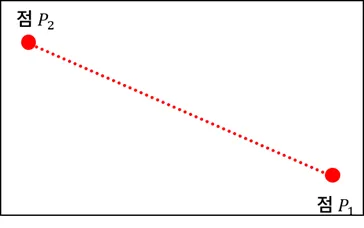
아핀 조합에 따른 점의 생성

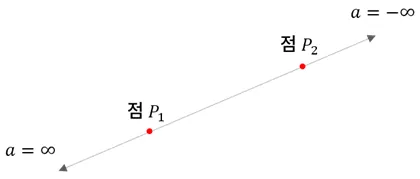
• $a$ 값에 따라 생성된 점들이 위 그림과 같이 같은 선상에 있음을 어떻게 증명할 수 있을 것인가?

선의 종류

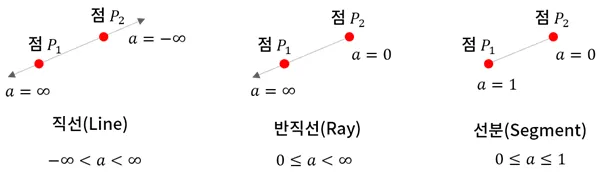
점의 표현

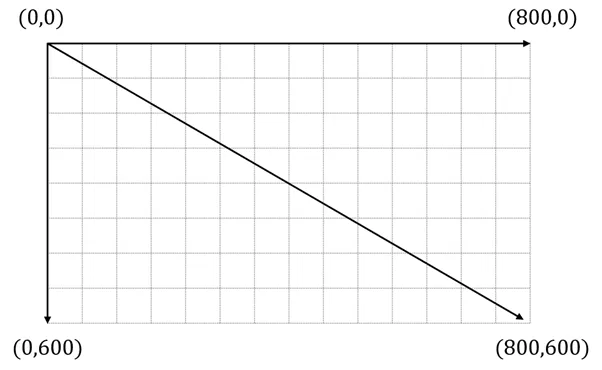
스크린 좌표계

• 화면은 픽셀들로 구성되어 있으며, 다음과 같은 좌표계를 사용하며 픽셀의 위치를 관리

• 수학에서 사용하는 데카르트 좌표계와 스크린 좌표계의 차이

  • 데카르트 좌표계

    • 실수 $\mathbb{R}$

    • 오른손 좌표계(우상방향 증가)

    • 연속성

  • 스크린 좌표계

    • 양의 정수 $\mathbb{H}$

    • 왼손 좌표계(우하방향 증가)

    • 이산성

  픽셀화 (Rasterization)

• 물체의 형상을 픽셀로 변환해 표현하는 작업

  

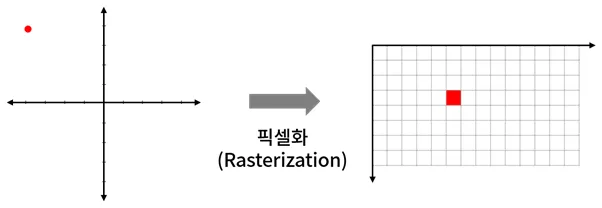
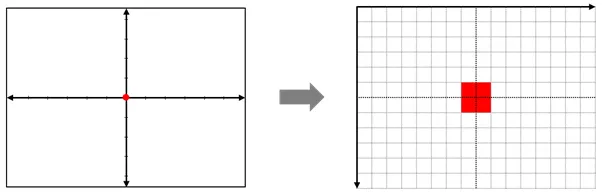
• 화면의 해상도가 짝수인 경우 $(0, 0)$을 표현하는데 한계가 발생

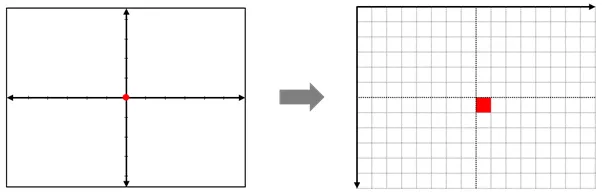
• 이 경우에는 지정된 규칙에 따라 네 개 중 하나의 픽셀을 선택할 수 밖에 없음

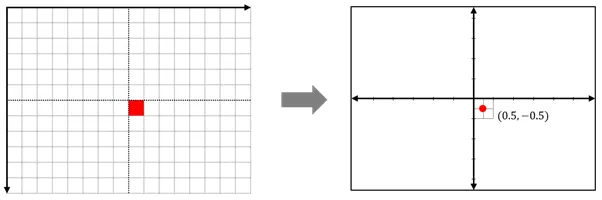
• 픽셀을 벡터로 변환할 때에는 픽셀 영역 하나의 대표값을 지정 해야 함

선 그리기 알고리즘 (브레젠험 알고리즘)

• 직선의 방정식으로 그리기

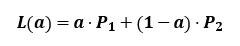
• 이론적으로는 다음과 같이 그릴 수 있으나 실용적인 방법 x

• 스크린 좌표계에서 픽셀 좌표는 정수로 고정

• 1962년도에 고안된 정수 연산만을 사용해 빠르게 선을 그리는 알고리즘
• 중점 (Mid-point) 알고리즘이라고도 함

브레젠험 알고리즘 구현 방법

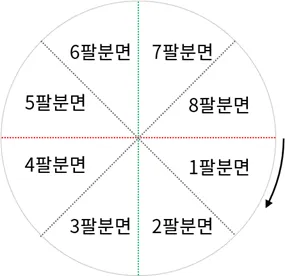
• 화면 공간을 8등분 하고 1 ~ 8 분면 (Octant)으로 나눔

• 직선의 방정식은 다음과 같음

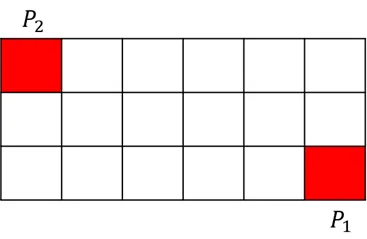
• 정수로 된 스크린 좌표계의 두 점의 좌표가 주어졌을 때 다음 정보가 주어짐
  • Width (너비) : $x_1 - x_0$
  • Height (높이) : $y_1 - y_0$
  • $x_0, y_0$ (시작 점의 좌표)
• 이를 바탕으로 위의 방정식을 변형

• 그렇다면 위의 식은 다음과 같이 전개

• 위의 식을 기본으로 모든 것을 전개

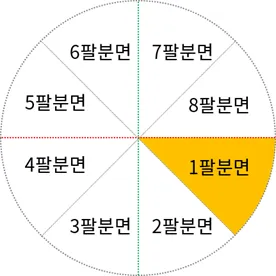
제 1팔분면

• 해당 영역에서는 기울기가 1을 넘어설 수 없는 특징을 가짐

• 그렇기 때문에 평행이동하거나 1칸 아래로 이동하는 동작만 발생

  • 시작점을 찍은 후 다음 점이 평행 이동하는지 한칸 아래로 내려가는지는 중점 값을 보고 판단

  

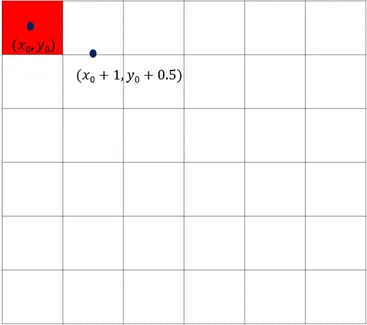
• 직선의 방정식 우변 $ax+b$의 값이 좌변 $y$보다 작다면 위의 픽셀을 선택하고 크면 아래 픽셀을 선택

• $x$값이 $x_0+1$인 경우 얻어지는 $y$값은 다음과 같음

• 이 값과 $y_0+0.5$와 비교한다. 그렇다면 평행 이동하는 경우는 다음과 가틍ㅁ

• 위 수식은 다음과 같이 단순화

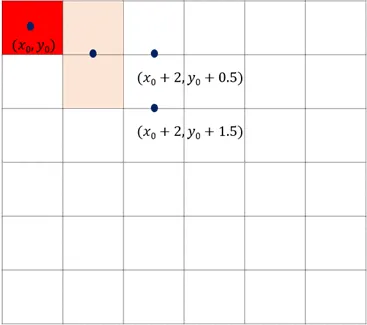
• 그 다음 위치 $(x_0+2)$ 상황에서는 세 점 중 하나를 선택

• 이 때에는 두 중점마다 판별식이 달라진다.

  • $4h-w$
  • $4h-3w$

  

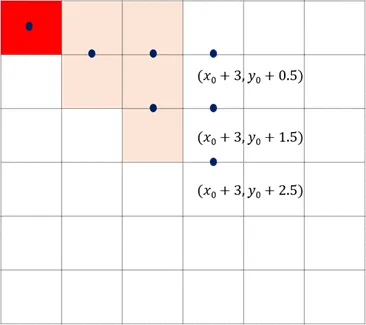
• 그 다음 지점 $(x_0+3)$에는 세 중점이 있고 각각의 판별식은 다음과 같음

  • $6h-w$
  • $6h-3w$
  • $6h-5w$

• 따라서 $x$가 증가할 때마다 판별 결과에 따라 판별식은 다음과 같이 변화된다고 할 수 있음

  • 평행 이동할 때는 $2h$만큼 증가
  • 아래로 내려갈 때는 $2h-2w$만큼 증가

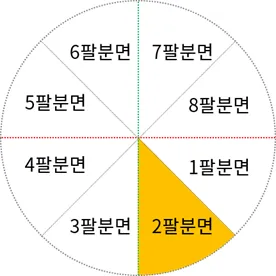
나머지 팔분면의 처리

• 제 2 팔분면은 $x$가 증가하지 않고 $y$를 증가시키는 방향으로 전개

• $x$와 $y$가 바뀐 상태로 동일하게 알고리즘을 진행하면 되며 판별식은 $2w-h$

• 3팔분면은 2팔분면에서 $x$를 거꾸로 증가시키는 형태이고 4팔분면은 1팔분면에서 $x$방향이 반대로 진행되는 것 외에는 동일

• 이전의 알고리즘에서 앞에 다음과 같은 요소를 고려해 보완하면 모든 팔분면의 처리가 가능

  • 경사가 완만한가 급격한가?
  • $x$방향과 $y$방향은 양의 방향인가 음의 방향인가?