벡터

벡터 (Vector)의 정의

수 직선에서의 표현의 한계

• 수를 점으로 표현한다면 1차원의 도형 수직선 위에 있는 것들만 표현이 가능
• 1차원 상에서 의미있는 무언가를 표현하기에는 주어진 공간이 너무 부족

데카르트 좌표계 (Cartesian Coordinate System)

• 수의 시스템을 기반으로 영역을 확장해 표현하는 방식
• 두 실수 집합을 교차시켜서 평면을 표현하고 오른쪽과 위쪽을 + 방향으로 지정

• 이렇게 영역을 확장한 모습은 두 실수 집합을 곱집합으로 확장한 $\mathbb{R} \times \mathbb{R}$ 로 볼 수 있음
• 곱집합의 원소는 순서쌍이므로 두 집합의 원소를 각각 미지수 $x$와 $y$로 두면 이는 $(x, y)$로 표현할 수 있음
• 이를 좌표 (Coordinate) 라고 함

2차원 평면의 시각화

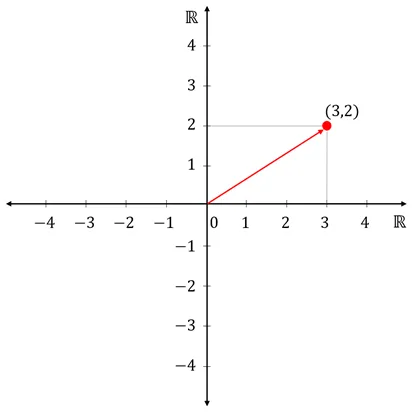
• 좌표에 해당하는 대상을 점으로 표현하면 다음과 같음
• 수와 동일하게 지정한 위치에 점을 찍거나 원점으로부터 화살표로 표현 가능

직선과 평면의 비교

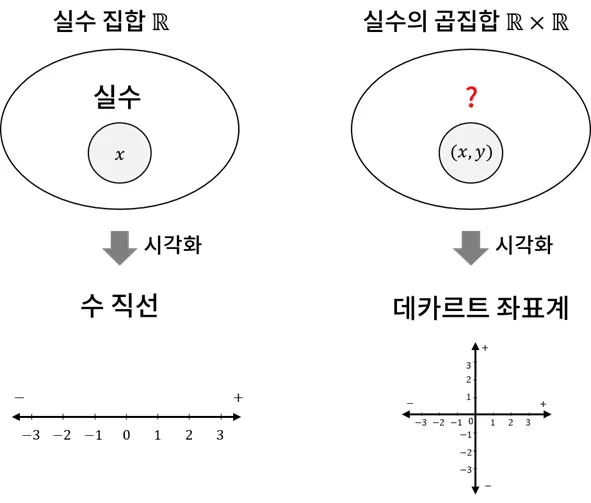
• 이러한 확장된 실수의 곱집합 $\R \times \R$ 의 공간 체계는 수는 아니기 때문에 이의 대상을 규정할 필요가 있음

벡터 (Vector)와 벡터 공간 (Vector Space)

• 이 대상은 특정 수집합을 지정하는 것이 아닌, 보편적인 수의 구조를 사용해 정의

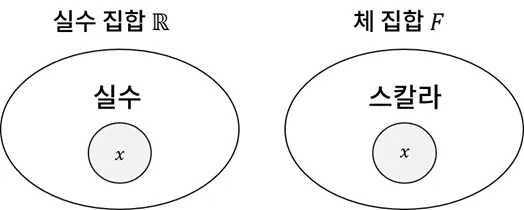
• 집합 : 체의 성질을 가지는 수 집합의 곱집합으로부터 만들어낸 대상
• 원소 : 스칼라의 순서쌍

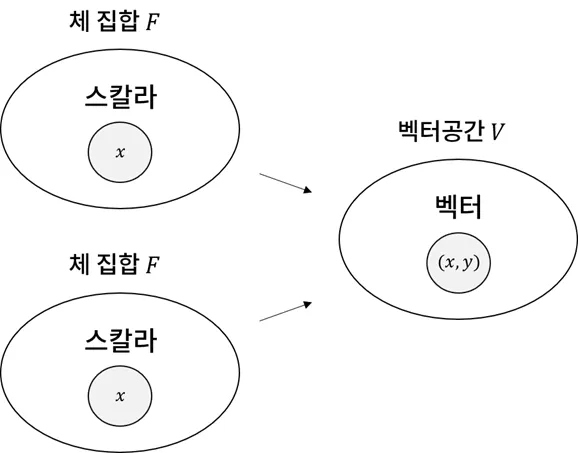
• 벡터 공간은 집합, 벡터는 원소의 개념

벡터의 연산 (Vector Operations)

• 벡터 공간이 변환되기 위해서는 수의 이항 연산과 같이 벡터를 사용해 새로운 벡터를 생성하는 시스템 필요
• 이를 위해 벡터에 대한 연산이 필요
• 벡터 공간에는 다음의 기본 연산이 정의 되어 있음

벡터의 기본 연산

벡터와 벡터의 덧셈

• 벡터와 벡터의 덧셈
  • $(a, b) + (c, d) = (a + c, b + d)$

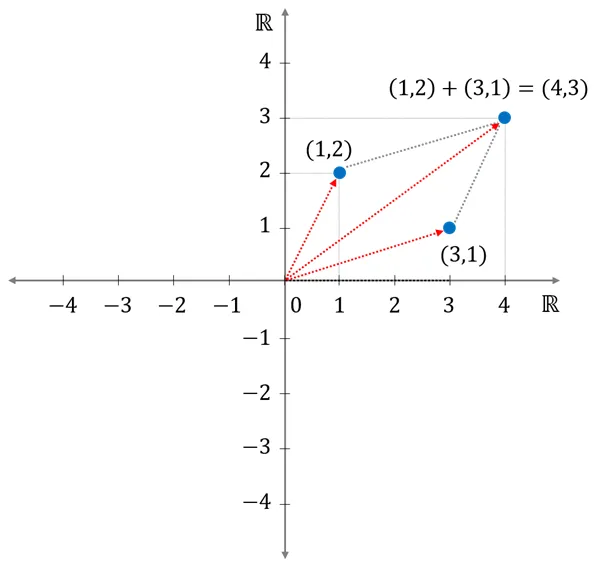
비유
물 10 mL와 기름 20 mL가 담긴 컵이 있다. 여기에 물 30 mL와 기름 10 mL가 담긴 컵을 서로 혼합할 때 만들어지는 물과 기름의 양은? 40 mL, 30 mL

x 좌표는 x 좌표끼리 y 좌표는 y 좌표끼리만 계산

• 두 실수 집합이 직교한다는 것은 물과 기름처럼 서로 연관성 없이 독립적으로 동작함을 의미

벡터와 스칼라의 곱셈

• $k · (a, b) = (ka, kb)$
• $(a, b) · k = (ak, bk)$

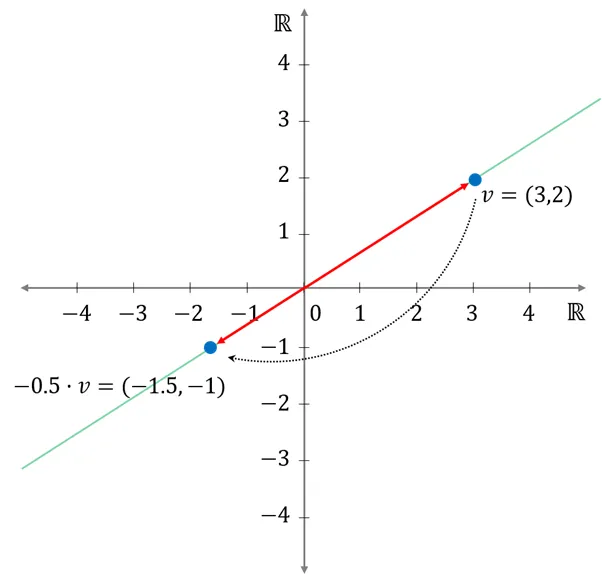
• 이후에 배울 중요한 벡터의 연산
  • 벡터의 내적 (Dot Product)
  • 벡터의 외적 (Cross Product)

벡터의 크기 (Norm)

• 수의 크기 = 원점으로 부터의 거리 $|x|$
• 벡터의 크기 = 원점으로 부터 최단거리 $|v|=\sqrt{x^2+y^2}$ 노름(Norm)이라고도 함.
• 벡터의 크기는 $||v||$로도 표현하지만 간결하게 |v|도 사용

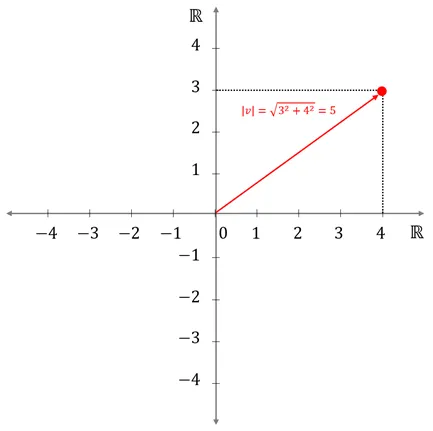
• 단위 벡터 : 크기가 1인 벡터
• 벡터의 크기의 역수 (Reciprocal)를 곱하면 단위 벡터가 만들어짐
• 따라서 단위 벡터를 만드는 공식 : $\hat{u}=\frac{v}{|v|}$

벡터 공간의 공리

• 이러한 벡터의 연산은 벡터 공간이라는 큰 집합의 개념에서 새로운 벡터를 생성하는 닫힌 시스템으로 바라봐야 함
• 이러한 벡터 공간의 시스템 은 항상 수를 시스템적인 측면에서 분석한 체 (Field)의 시스템을 기반으로 확장해 만든 시스템으로 볼 수 있으며, 이는 8개의 공리로 구성되어 있음
  • 참고 : $u,v,w$는 벡터를 의미하고 $a,b$는 스칼라를 의미함.

1. 덧셈의 연산의 결합 법칙
   $u+(v+w)=(u+v)+w$

2. 덧셈 연산의 교환법칙
   $u+v=v+u$

3. 덧셈연산의 항등원
   $v+\vec{0}=v$ ( $\vec{0}$은 영벡터를 의미 )

4. 덧셈 연산의 역원
   $v+(-v)=\vec{0}$

5. 스칼라 곱셈 연산의 호환성 (Compatibility)
   $a(bv)=(ab)v$

6. 스칼라 곱셈 연산의 항등원
   $1v=v$

7. 벡터 덧셈과 스칼라 곱셈의 분배법칙
   $a(u+v)=au+av$

8. 스칼라 덧셈과 스칼라 곱셈의 분배법칙
   $(a+b)v=av+bv$