1. 벡터의 생성 (Span) 시스템
선형 조합 (Linear Combination)
-
벡터의 기본 연산을 사용해 새로운 벡터를 생성하는 수식
선형 의존과 선형 독립의 수학적 정의
-
다음 수식을 만족하는 0이 아닌 계수가 존재하면 수식 내 벡터들은 선형 의존
-
다음 수식을 만족하기 위해 어떤 계수 값이 0이라면 수식 내 벡터들은 선형 독립
문제) (1, 1)과 (2, 2)는 선형 의존인가 선형 독립인가?
a1 = 2, a2 = -1을 사용하면 영 벡터가 만들어진다.
0 이 아닌 계수를 사용하여 영벡터를 만들어 낼 수 있다.
따라서 두 벡터 (1, 1) 과 (2, 2)는 선형 의존이다.문제) (1, 2)와 (2, 1)은 선형 의존인가 선형 독립인가?
-
위 식은 다음과 같은 연립 방정식으로 정리할 수 있다.
위 식을 만족하는 값은 a1 = 0, a2 = 0 뿐이다. 따라서 두 벡터 (1, 2)와 (2, 1)는 선형 독립이다.선형 조합으로 새로운 벡터 생성하기
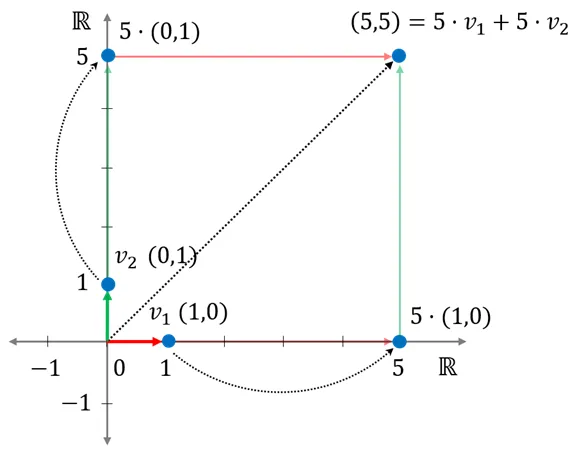
- 벡터 (5, 5)를 두 벡터의 조합으로 생성하는 방법
로 생성하기
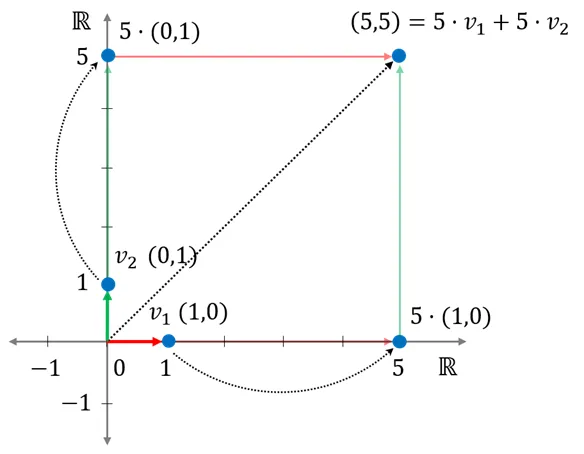
- 또는
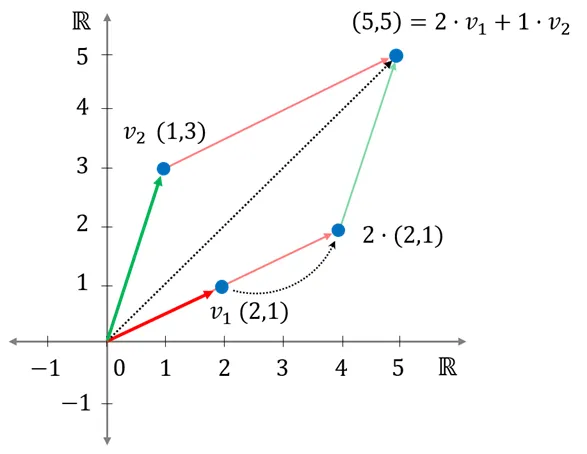
로 생성하기
-
그렇다면 두 벡터 (2, 1)과 (1, 3)을 조합해 평면 위의 모든 벡터의 생성이 가능한가?
-
이를 수식으로 나타내면
-
위 수식은 다음의 연립 방정식으로 변경할 수 있다.
-
위 식에서 a와 b를 구할 수 있기 때문에 모든 점의 생성이 가능
-
그렇다면 모든 두 벡터의 조합은 평면의 모든 점을 생성할 수 있을까?
- 벡터 (1, 2)와 (2, 4)의 경우
-
이 경우 다음의 연립방정식으로 변경 가능
-
이 경우에는 해가 존재하지 않고 오직 (x, 2x) 형태의 벡터만 생성 가능
-
이를 그림으로 나타내면 다음과 같음
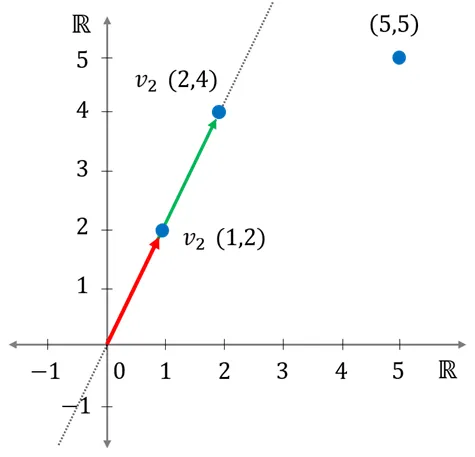
-
(2, 4)는 (1, 2)의 스칼라 곱으로 표현 가능하므로 위 수식은 사실상 (1, 2)의 스칼라 곱으로 표현되기 때문에 벡터 (1, 2)의 기울기와 동일한 벡터만 생성되기 때문
기저 (Basis)와 차원 (Dimension)
-
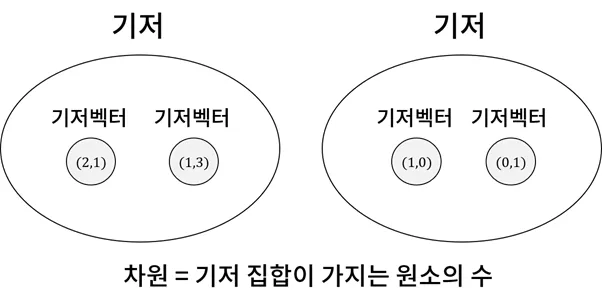
기저 (Basis) : 벡터 공간 내 모든 벡터를 생성할 수 있는 선형 독립인 벡터들의 집합
-
기저 벡터 (Basis Vector) : 기저 집합에 속한 원소
-
차원 (Dimension) : 기저 집합이 가지는 원소의 수
-
2차원 평면을 생성하기 위해서는 항상 두 개의 기저 벡터를 가짐
-
앞서서 (5, 5)를 만들기 위한 벡터의 조합은 두 가지가 있었음
-
모두 평면의 기저가 될 수 있고 무난히 많은 기저에 대한 경우의 수가 존재하지만, 기저 집합의 원소의 수는 언제나 두 개로 동일
-
기저가 하나라면 벡터와 스칼라의 곱셈 성질로 인해 하나의 선에 해당하는 벡터만 생성할 수 있고, 세 개 이상인 경우에는 선형 독립을 만족하지 못하기 때문
-
앞선 식에서 두 선형 독립인 벡터로 평면 상의 모든 점을 생성할 수 있음을 알 수 있음
-
그렇다면 아래의 식의 경우 0벡터를 만들기 위해 0이 아닌 세 번째 계수가 존재한다는 것을 의미
-
따라서 평면에서 세 개 이상의 원소를 구성된 기저는 존재하지 않음을 알 수 있음
-
실 벡터 공간을 표기할 때 이러한 차원의 정보를 사용해 첨자를 붙여 다음과 같이 표현
표준 기저 벡터 (Standard basis Vector)
- 기저벡터 중에서 가장 기본이 되는 벡터.
- 의 표준 기저벡터
- 의 표준 기저벡터