함수

함수 (Function)의 기초

함수를 왜 배워야 하는가?

• 게임의 공간을 구성하고 화면에 보여지는 전 과정은 대부분 공간과 공간의 변환으로 구성
• 이러한 변환은 근본적으로 집합과 집합의 대응 관계에 기반하고 있으며, 이의 메커니즘을 설명하는 이론이 함수

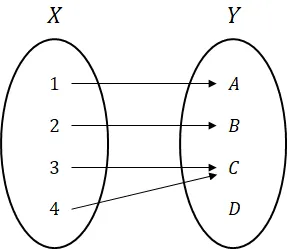
함수의 정의

• 함수의 성립 조건 : 첫번째 집합의 모든 요소가 사용되어야 함
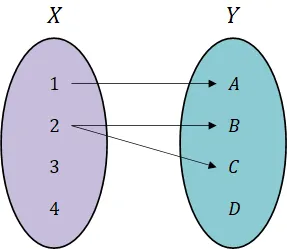
• 함수가 아닌 대응 관계
  • 첫번째 집합의 어떤 원소에 대한 대응 관계가 빠져 있을 때
  • 첫번째 집합의 한 원소가 두번째 집합의 두 가지 이상의 원소에 대응할 때

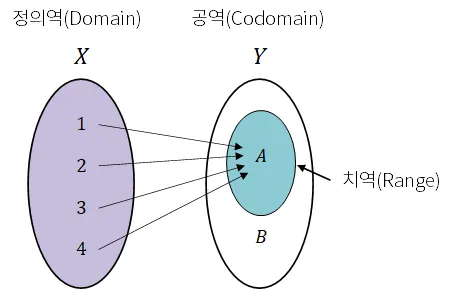
함수 관련 주요 용어

• 정의역 (Domain)
• 공역 (Codomain)
• 치역 (Range)

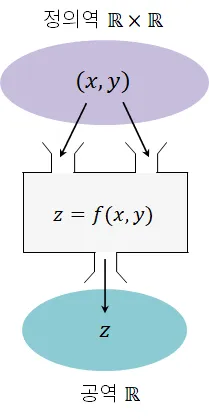
• 프로그래밍 관점에서 함수 바라보기
  • 입력 (Input)
  • 출력 (Output)

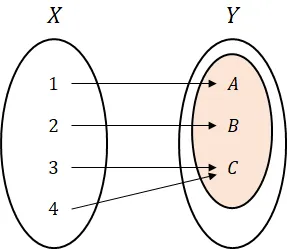
함수의 종류 (Classes of Function)

• 전사 (Surjection) : 공역과 치역이 동일

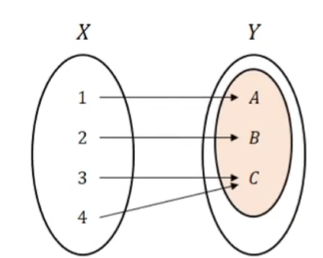
• 단사 (Injection) : 정의역과 공역의 요소가 1:1로 대응

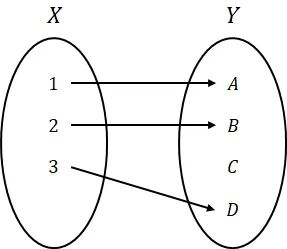
• 전단사(Bijection) : 전사 + 단사를 모두 만족

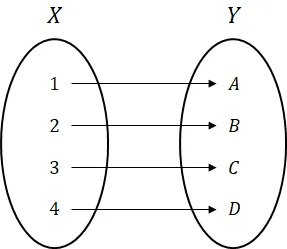
• 일반 (General)

곱집합 (Cartesian Product)

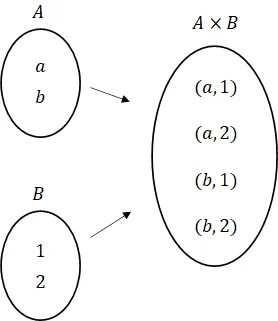
곱집합의 정의

• 곱집합이란 두 집합의 원소를 순서쌍으로 묶어 구성한 집합
• (a, b)와 같이 괄호와 콤마를 사용해 원소를 나열하는 방식을 튜플 (Tuple) 이라고 함
• 곱집합은 x 기호를 사용해 표현. 예) $A\times B$

곱집합의 예시

출처 : https://ko.wikipedia.org/wiki/%EA%B3%B1%EC%A7%91%ED%95%A9#/media/%ED%8C%8C%EC%9D%BC:Piatnikcards.jpg

집합 R = {A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2}
집합 S = {♠, ♥, ♣, ♦}
트럼프 : $R x S$

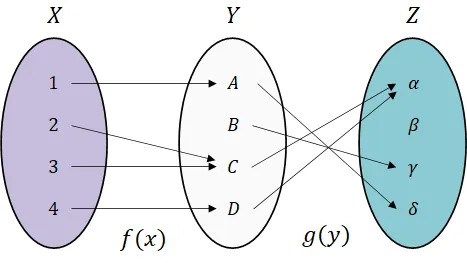
이항 연산을 함수로 해석하기

합성 함수 (Composition)

항등함수 (Identity Fuction)

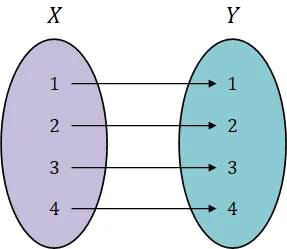
• 정의역의 요소와 공역의 요소가 대응되는 함수
• 항등 함수의 기호 : $i$

역함수 (Inverse Function)

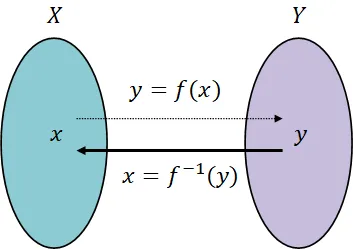
• 전단사 함수일 때 성립
• 공역에서 정의역으로 대응하는 관계로 바꾸는 함수

역함수의 조건

• 아래의 전사 함수는 역함수가 성립되지 않는다

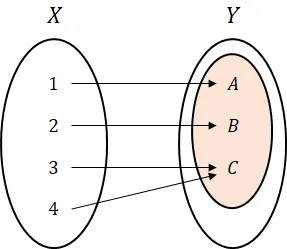
• 아래의 단사 함수는 역함수가 성립되지 않는다

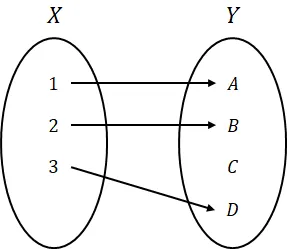
• 전단사 함수일 때만 역함수를 보장받는다.

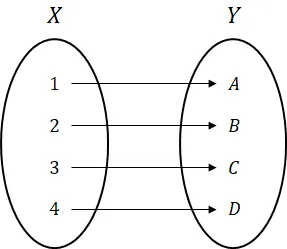
함수와 그 역함수의 합성 함수

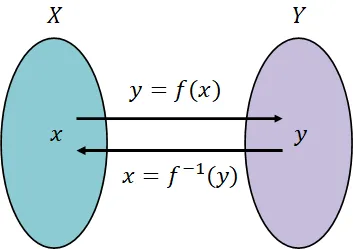
• 어떤 전단사 함수와 그 역함수와의 합성 함수는 항등함수가 된다

  $f\circ f^{-1}=i$

합성함수의 역함수

$(g\circ f)^{-1}=f^{-1}\circ g^{-1}$

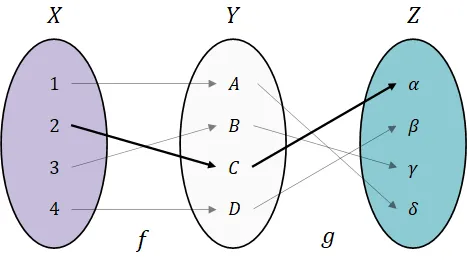
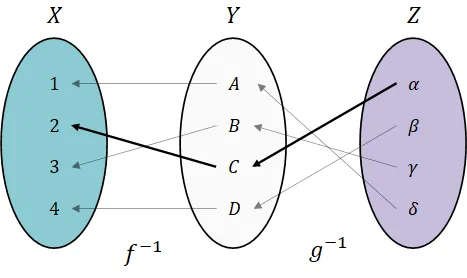
왜 이러한 합성함수의 대응관계를 알아야 하는가?

• 이후에 배울 행렬은 하나의 함수에 대응되고 행렬의 곲메은 합성 함수에 대응됨
• 이러한 합성함수의 성질을 이해하면 복잡한 행렬 연산의 메커니즘을 이해할 수 있는 기반이 됨