삼각형

Woogie_·2025년 5월 22일
게임 수학

게임 수학

목록 보기
12/15

세 점의 아핀 조합 (Affine Combination of Three points)

P′=s⋅P1+t⋅P2+(1−s−t)⋅P3P'=s\cdot P_1+t\cdot P_2 +(1-s-t)\cdot P_3
  • 세 점의 아핀 조합으로 만들 수 있는 공간의 형태는?
P′−P3=s(P1−P3)+t(P2−P3)w⃗=su⃗+tv⃗P'-P_3=s(P_1-P_3)+t(P_2-P_3) \\ \vec{w}=s\vec{u}+t\vec{v}

  • 여기서 u⃗와v⃗\vec{u}와 \vec{v}가 선형 독립이면?

    • 위 조합에서 각 계수에 0≤s≤1,0≤t≤1,0≤(1−s−t)≤10\leq s\leq 1 , 0\leq t\leq1, 0\leq (1-s-t) \leq1 조건이 붙으면 어떻게 될까?

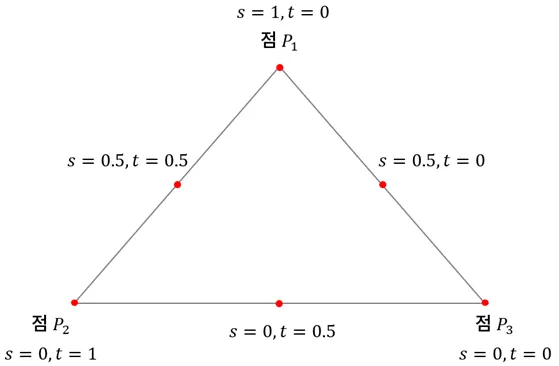
컨벡스 조합 (Convex Combination)

  • 아핀 조합에서 모든 계수의 크기가 0보다 크고 1보다 작은 경우를 컨벡스 조합

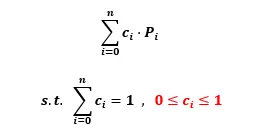
  • 컨벡스 조합을 통해 실제로 사용할 수 있는 형상이 완성

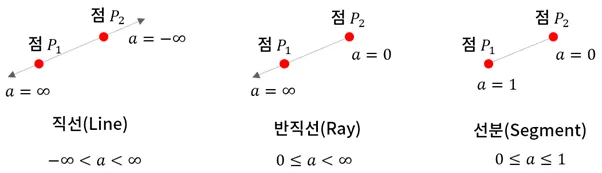
볼록 (Convex)와 오목 (Concave)

  • 임의의 두 점이 연결한 선이 영역을 벗어나면 오목하다고 표현

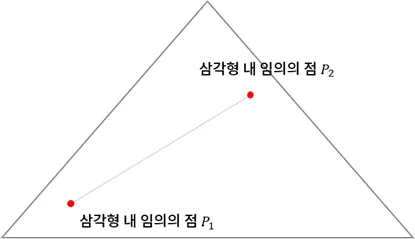
볼록함 (Convexity)

  • 영역 내 임의의 점을 연결한 건이 영역을 벗어나지 않는 성질

네 점의 컨벡스 조합

  • 네 점의 컨벡스 조합은 조합에서 만들어지는 각 벡터가 선형 독립인 경우 다음과 같은 사면체가 나옴
P′=a⋅P1+b⋅P2+c⋅P3+(1−a−b−c)⋅P4x⃗=au⃗+bv⃗+cw⃗P'=a\cdot P_1+b\cdot P_2 + c\cdot P_3 + (1-a-b-c)\cdot P_4\\ \vec{x}=a\vec{u}+b\vec{v}+c\vec{w}

메시 (Mesh) 구조

  • 수학으로 만들어지는 컨벡스 영역 중에서 가장 효과적으로 활용할 수 있는 도형은 삼각형
    • 2차원 영역의 표현 가능
    • 3차원은 2차원 표면을 조합해 표현 가능
  • 3차원 물체는 삼각형을 조합해 다음과 같이 생성

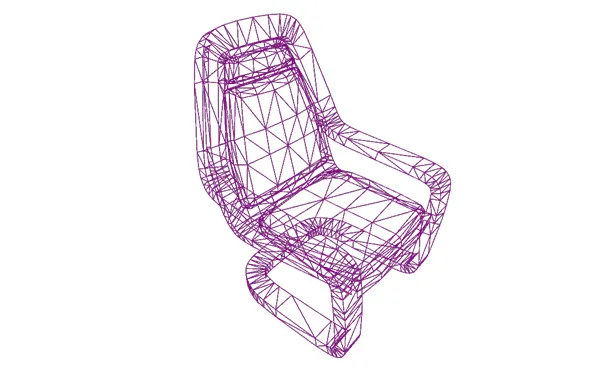
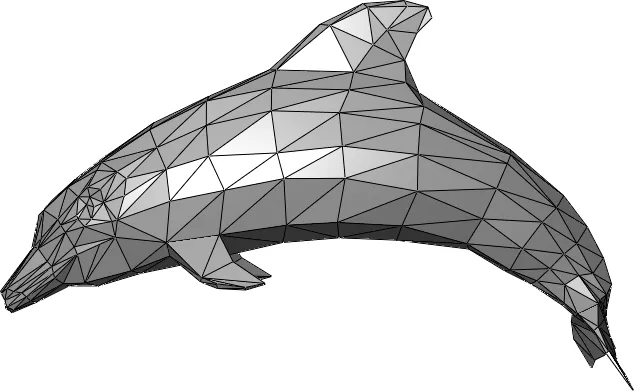
메시 구조

  • 정점과 삼각형 정보를 별도로 구성하는 삼각형 리스트 (Triangle List) 방식을 사용

  • 정점 버퍼에는 정점을 모아두고 인덱스 버퍼에는 삼각형 정보를 모아둠

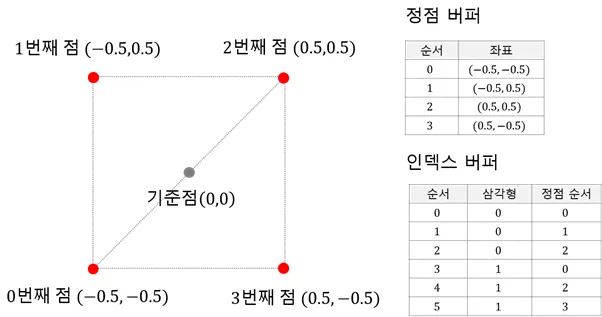
  • 삼각형 두 개로 구성되는 사각형은 다음과 같이 설계할 수 있음

    • 이 때 두 삼각형이 겹치는 정점은 재활용해 배치가 가능

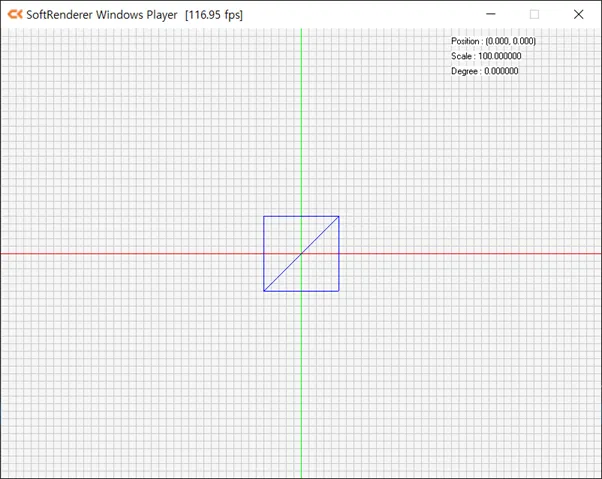
와이어프레임 (Wireframe)

  • 삼각형마다 점을 연결해 선 그려 메시를 형상화한 결과화면

무게중심좌표 (Barycentric Coordinate)

  • 다음과 같은 아핀 조합의 식에서
s⋅P1+t⋅P2+(1−s−t)⋅P3s\cdot P_1+t\cdot P_2 +(1-s-t)\cdot P_3
  • 세 계수를 조합해 $(s, t, 1 - s - t) 생성한 좌표를 무게중심좌표라고 함

무게 중심 좌표의 계산방법

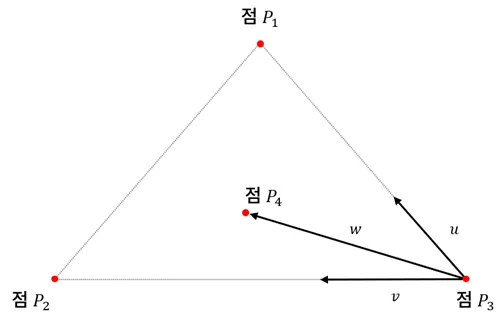
  • 동일한 평면위의 점 P4P_4 대한 무게 중심 좌표를 구하는 방법은 다음과 같음
w⃗=s⋅u⃗+t⋅v⃗\vec{w}=s\cdot \vec{u}+t\cdot \vec{v}
  • 양변에 u,vu, v를 내적
w⋅u=s(u⋅u)+t(v⋅u)w⋅v=s(u⋅v)+t(v⋅v)w\cdot u=s(u\cdot u)+t(v\cdot u)\\ w\cdot v=s(u\cdot v)+t(v\cdot v)
  • 양변에 (u⋅v)(u\cdot v)와 (u⋅u)(u\cdot u)를 곱하기

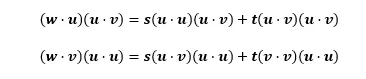
  • 양변을 소거하면 다음의 결과가 나옴

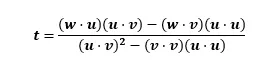
  • 동일한 방법으로

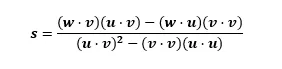
무게중심좌표의 활용 - 삼각형 채우기

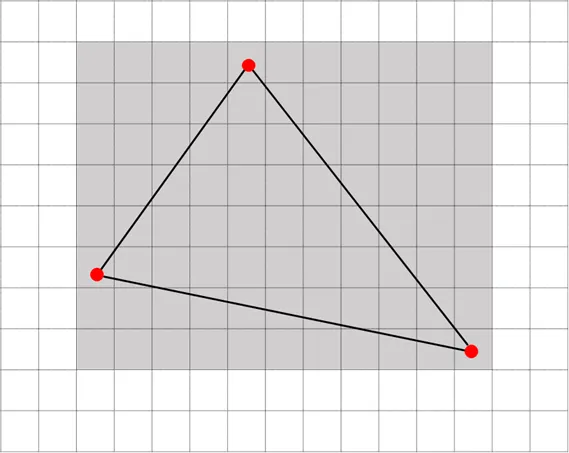
  • 이 중에서 컨벡스 조건을 만족하는 픽셀만 그린 결과 화면

profile
Woogie_
상상을 구현하는 개발자
이전 포스트

직선

다음 포스트

텍스쳐 매핑

0개의 댓글