Welcome to Time Series!
예측, Forecasting은 ML이 가장 많이 활용되는 분야일 것이다.
- 기업은 제품 수요를 예측
- 정부는 경제 및 인구 증가를 예측
- 기상학자는 날씨를 예측
시계열 예측, Time Series forecasting은 오랜 역사를 가진 광범위한 분야이다.
이 course를 마치면 다음과 같은 방법을 알게 될 것이다.
- 주요 시계열 feature(추세, 계절, 주기)를 모델링하는 기능을 engineering
- 다양한 종류의 시계열 plot으로 시계열을 시각화
- 상호 보완적인 모델의 강점을 결합한 예측 하이브리드를 만드는 방법
What is Time Series?
예측의 기본 대상은 시간에 따라 기록된 일련의 관측치인 시계열이다. 예측 application에서의 관측값은 일반적으로 일별 또는 월별과 같이 일정한 빈도로 기록된다.
import pandas as pd
df = pd.read_csv(filepath,
index_col = 'Date',
parse_dates=['Date'],
).drop('Paperback', axis=1)
df.head()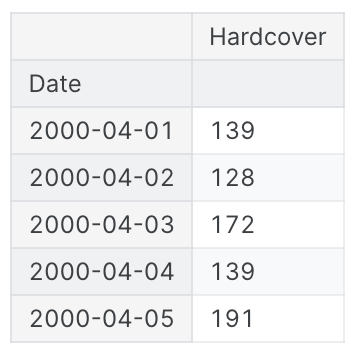
이 시리즈는 30일 동안 소매점에서 판매된 하드커버 도서의 수를 기록한다. 시간 인덱스 날짜가 있는 single column의 관찰 항목 하드 커버가 있음을 알 수 있다.
Linear Regression with Time Series
이 과정의 첫 번째 파트에서는 Linear Regression 알고리즘을 사용하여 예측 모델을 구축한다.
선형 회귀는 실무에서 널리 사용되며 복잡한 예측 작업에도 자연스럽게 적응한다.
선형 회귀 알고리즘은 input features에서 weighted sum(가중 합계)를 만드는 방법을 학습한다.
두 feature의 경우
target = weight_1 * feature_1 + weight_2 * feature_2 + bias학습하는 동안, regression 알고리즘은 대상에 가장 적합한 매개변수 weight_1, weight_2 및 bias에 대한 값을 학습한다.
(이 알고리즘은 대상과 예측 간의 squared error를 최소화하는 값을 선택하기 때문에 일반 최소 제곱법 이라고도 한다.)
가중치는 Regression coefficient (회귀 계수) 라고도 하며, bias는 이 함수의 그래프가 Y축을 교차하는 위치를 알려주기 때문에 절편이라고도 한다.
Time-step features
여기에는 시계열에 고유한 두 가지 종류의 기능, 즉 time-step features(시간 단계 기능)와 lag features(지연 기능)가 있다.
Time-stop features는 time index에서 직접 도출할 수 있는 기능이다.가장 기본적인 Time-step 기능은 시계열의 시작부터 끝까지 시간 단계를 카운트 오프하는 시간 더미이다.
import numpy as np
df['Time'] = np.arange(len(df.index))
df.head()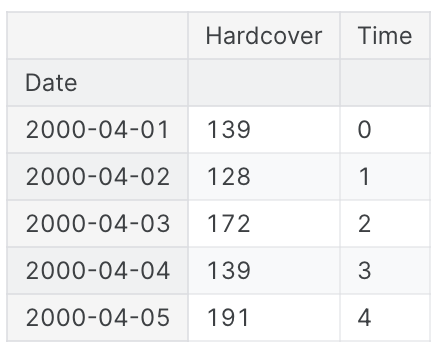
시간 더미를 사용한 Linear Regression은 모델을 생성한다.
target = weight * time + bias그 후 시간 더미를 사용하면 시간이 X축을 사용하는 시간 plot에서 곡선을 시계열에 맞출 수 있다.
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("seaborn-whitegrid")
plt.rc(
"figure",
autolayout=True,
figsize=(11, 4),
titlesize=18,
titleweight='bold',
)
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=16,
titlepad=10,
)
%config InlineBackend.figure_format = 'retina'
fig, ax = plt.subplots()
ax.plot('Time', 'Hardcover', data=df, color='0.75')
ax = sns.regplot(x='Time', y='Hardcover', data=df, ci=None, scatter_kws=dict(color='0.25'))
ax.set_title('Time Plot of Hardcover Sales');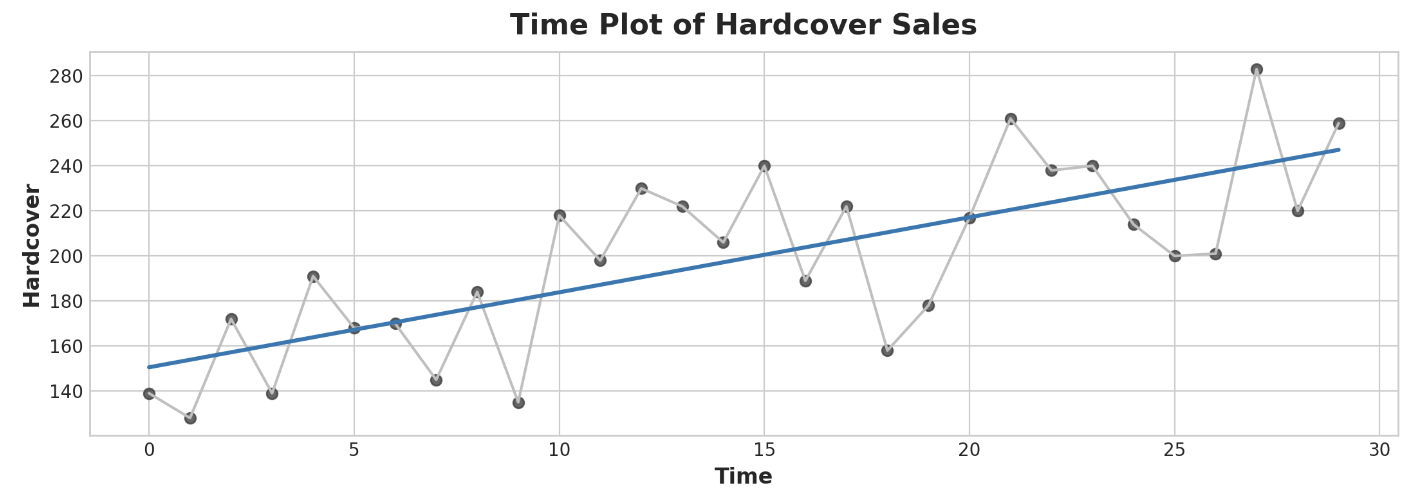
Time-stop features를 사용하면 시간 종속성을 모델링할 수 있다. 값이 발생한 시점을 기준으로 값을 예측할 수 있는 경우 계열은 시간 종속적이다.
Hard cover 판매량 시리즈에서는 일반적으로 월 후반의 판매량이 월 초반의 판매량보다 높다는 것을 예측할 수 있다.
Lag features
Lag features를 만들려면 대상 계열의 관측값을 이동하여, 나중에 발생한 것처럼 보이도록 한다. 여기서는 1단계 지연 기능을 만들었지만 여러 단계로 이동하는 것도 가능하다.
df['Lag_1'] = df['Hardcover'].shift(1)
df = df.reindex(columns=['Hardcover', 'Lag_1'])
df.head()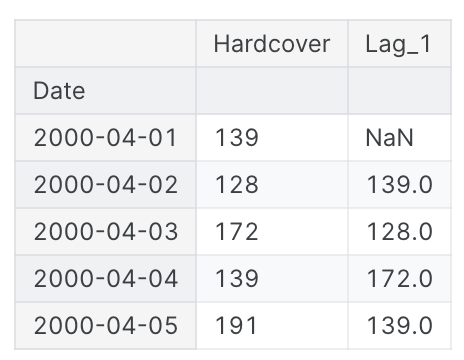
가장 첫번째 행만 NaN, 한 값씩 밀린 열인 것을 알 수 있음
Lag feature를 사용한 Linear Regression은 model를 생성한다.
target = weight * lag + bias따라서 Lag feature를 사용하면 계열의 각 관측값을 이전 관측값과 비교하여 그래프를 그리는 Lag plot에 곡선을 맞출 수 있음
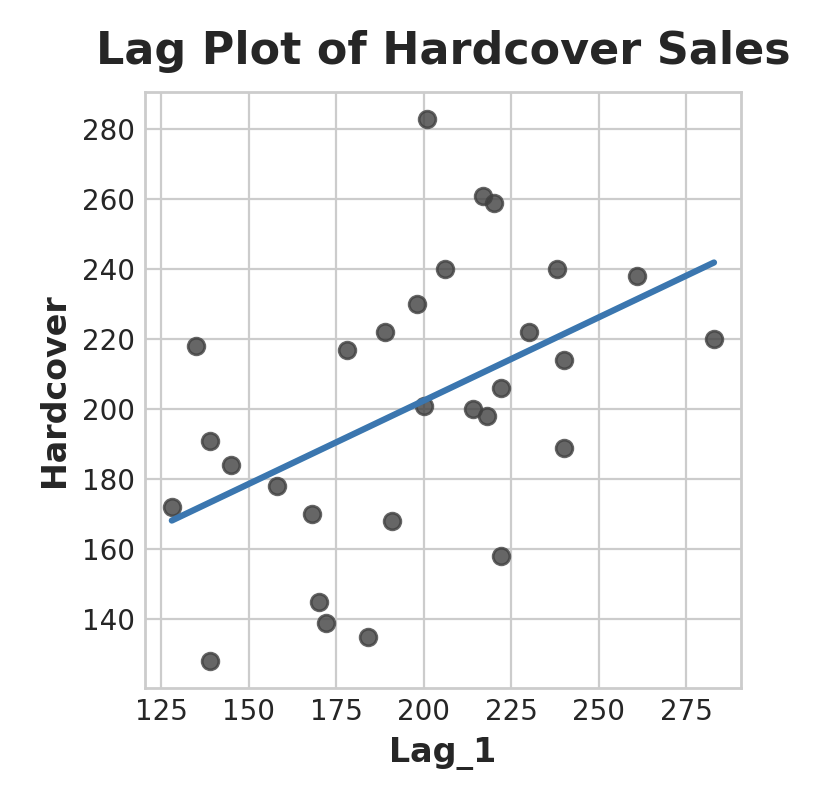
Lag plot에서 하루 판매량(Hard cover)이 전 날의 판매량(Lag_1)과 상관관계가 있음을 알 수 있다.
이와 같은 관계를 볼 수 있다면 Lag features가 유용하다는 것을 알 수 있음
더 일반적으로, Lag features를 사용하면 직렬 의존성을 모델링할 수 있다.
시계열은 이전 관측치를 통해 다음 관측치를 예측할 수 있을 때 직렬 의존성을 갖는다. Hard cover 판매량에서 하루의 높은 판매량은 일반적으로 다음 날의 높은 판매량을 의미한다고 예측할 수 있다.
ML 알고리즘을 시계열 문제에 적용하는 것은 주로 time index와 lag을 사용한 feature engineering에 관한 것이다. 대부분의 경우 단순성을 위해 linear regression을 사용하지만 이러한 기능은 예측 작업에 어떤 알고리즘을 선택하든 유용하게 사용할 수 있다.
Example - Tunnel Traffic
Tunnel Traffic은 2003년 11월부터 2005년 11월까지 매일 스위스의 바레그 터널을 통과하는 차량 수를 설명하는 시계열이다. 이 에에서는 linear regression을 Time-step features와 lag feature에 적용하는 연습을 한다.
from pathlib import Path
from warnings import simplefilter
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
simplefilter("ignore") # ignore warnings to clean up output cells
# set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=14,
titlepad=10,
)
plot_params = dict(
color="0.75",
style=".-",
markeredgecolor="0.25",
markerfacecolor="0.25",
legend=False,
)
%config InlineBackend.figure_format = 'retina'
data_dir = Path(filepath)
tunnel = pd.read_csv(data_dir / "tunnel.csv", parse_dates=["Day"])
# 판다스에서 인덱스를 날짜컬럼으로 설정하여 시계열을 만듬
# 데이터를 로드할 때 'parse_dates'를 사용하여 'Day'를 날짜유형으로 만듬
tunnel = tunnel.set_index("Day")
tunnel = tunnel.to_period()
tunnel.head()기본적으로 판다스는 단일 순간에 측정된 일련의 측정값으로 시계열을 나타내는 'np.datetime64'에 해당하는 dtype 'Timestamp'로 'DatetimeIndex'를 생성한다.
반면에 'PeriodIndex'는 시계열을 일정 기간 동안 누적된 수량 시퀀스로 나타낸다. Periods가 더 작업하기 쉬운 경우가 많으므로 이 강좌에서는 기간을 사용한다.
Time-step feature
시계열에 누락된 날짜가 없다면 시계열의 길이를 계산하여 시간 더미를 만들 수 있다.
df = tunnel.copy()
df['Time'] = np.arange(len(tunnel.index))
df.head()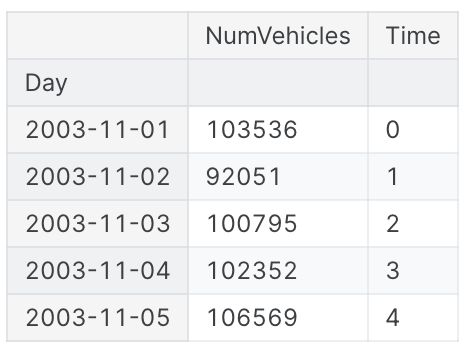
Linear Regression 모델을 맞추는 절차는 scikit-learn의 표준 단계를 따름
from sklearn.linear_model import LinearRegression
# training data
X = df.loc[:, ['Time']] #features
y = df.loc[:, ['NumVehicles']] #target
# train the model
model = LinearRegression()
model.fit(X, y)
y_pred = pd.Series(model.predict(X), index=X.index)실제로 생성된 모델은 대략 다음과 같다.
차량 = 22.5 * 시간 + 98176
시간에 따른 적합 값을 plotting 하면, 어떻게 시간 더미에 선형회귀를 맞추어 이 방정식으로 정의된 추세선이 생성되는지 알 수 있다.
ax = y.plot(**plot_params)
ax = y_pred.plot(ax=ax, linewidth=3)
ax.set_title('Time Plot of Tunnel Traffic');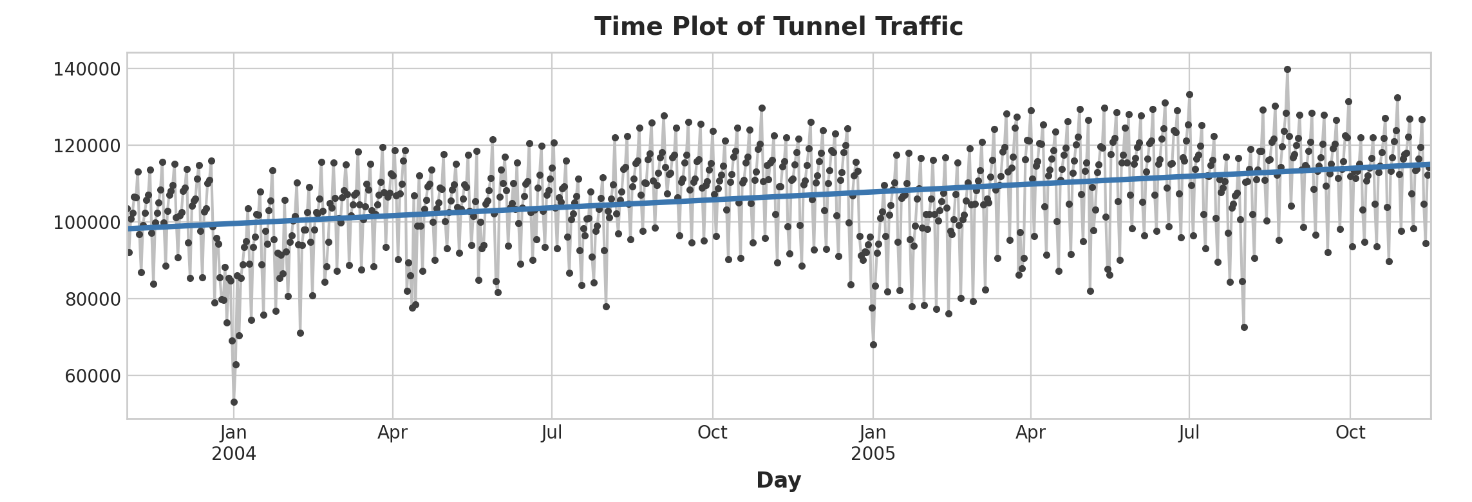
Lag feature
판다스는 시리즈를 지연시키는, shift라는 메소드를 제공한다.
df['Lag_1'] = df['NumVehicles'].shift(1)
df.head()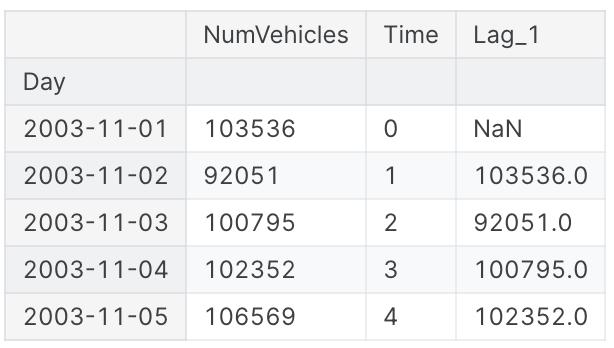
Lag feature를 만들 때 생성된 결측값을 어떻게 할지 정해야 함
0.0으로 채우거나, 알려진 첫번째 값으로 "backfilling" 하는 것도 방법이다.
그냥 삭제하는 것도 됨
from sklearn.linear_model import LinearRegression
X = df.loc[:, ['Lag_1']]
X.dropna(inplace=True)
y = df.loc[:, 'NumVehicles']
y, X = y.align(X, join='inner') # drop corresponding values in target
model = LinearRegression()
model.fit(X, y)
y_pred = pd.Series(model.predict(X), index=X.index)Lag plot은 하루의 차량 수와 전 날의 차량 수 사이의 관계를 얼마나 잘 맞출 수 있었는지를 보여준다.
fig, ax = plt.subplots()
ax.plot(X['Lag_1'], y, '.', color='0.25')
ax.plot(X['Lag_1'], y_pred)
ax.set_aspect('equal')
ax.set_ylabel('NumVehicles')
ax.set_xlabel('Lag_1')
ax.set_title('Lag Plot of Tunnel Traffic');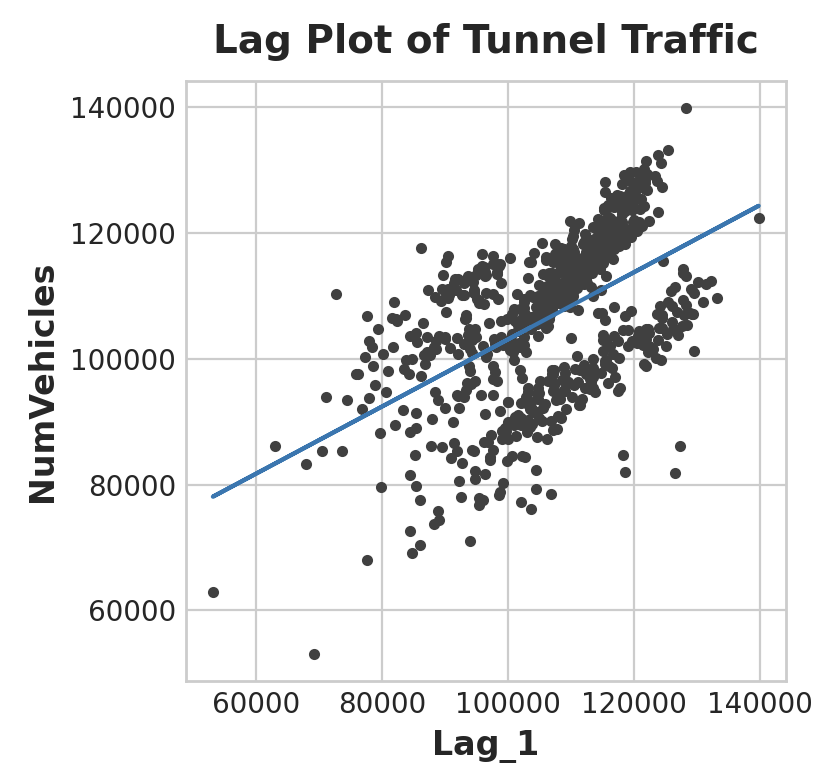
다음 time plot은 현재 예측이 최근 과거의 계열의 동작에 대해 어떻게 반응하는지 보여준다.
ax = y.plot(**plot_params)
ax = y_pred.plot()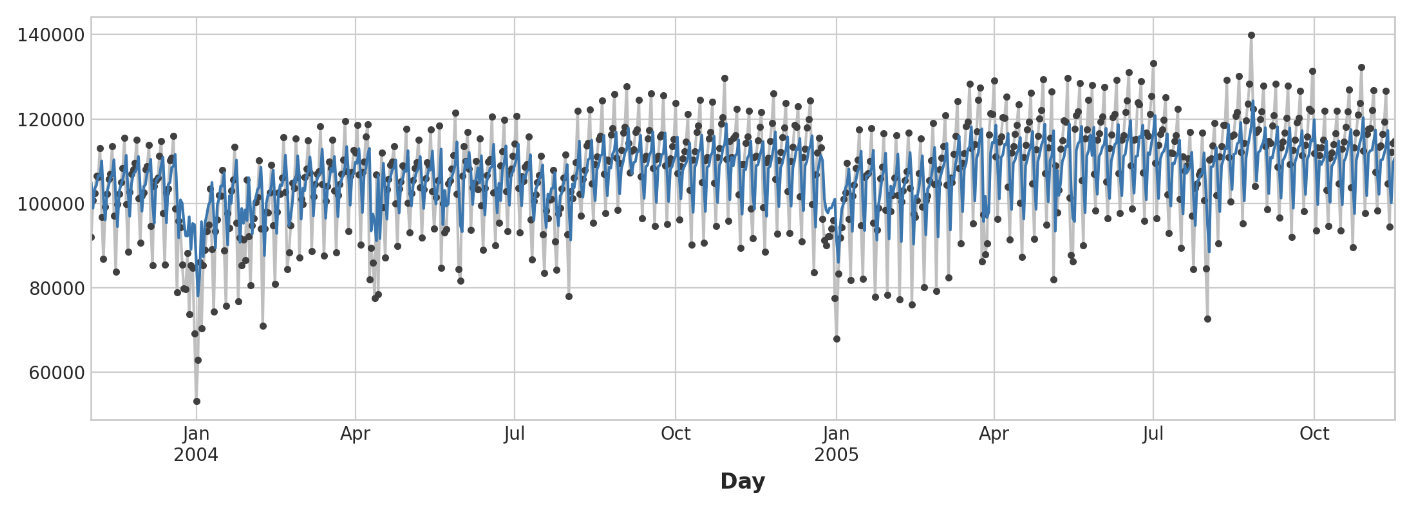
가장 좋은 시계열 데이터는 일반적으로 time-step features와 Lag features의 조합이 포함된다. 다음 몇 단원에서는 이 단원의 기능을 시작점으로 삼아 시계열에서 가장 일반적인 패턴을 모델링하는 기능을 engineering한다!
