[RetNet 논문 리뷰](A Successor to Transformer for Large Language Models)

김태민·2023년 7월 29일

AI RetNet 논문리뷰

boostcamp

목록 보기

11/36

[RetNet](A Successor to Transformer for Large Language Models)

1. 논문이 다루는 Task

Task: Text Generation

Input: Text
Output:Text
Text Generation : 텍스트 생성 모델이다.

2. 기존 연구 한계

2-2. Transformer의 단점

트랜스포머는 기존 순차적인 훈련을 극복하기 위해 제안되었지만 단계당 $O(N)$ 의 복잡성과 키-값으로 인한 메모리 문제로 인해 배포하기에는 적합하지않다고 주장한다.

2-3. Variants Transforemr

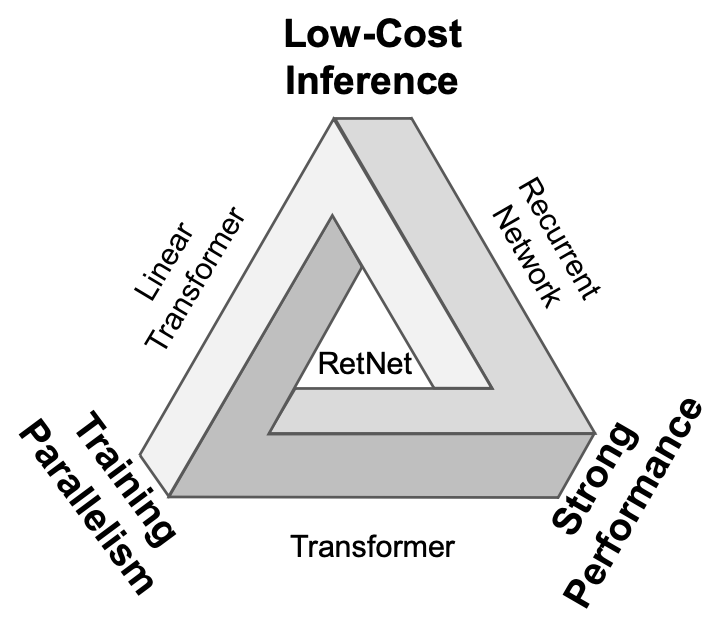
각종 변형된 Transformer 모델을 가져오더라도 맨 위의 그림과 같이 삼각형의 문제의 직면하게 된다. 이 모두를 달성한 모델이 RetNet이다.

3. 제안 방법론

트랜스포머와 같은 훈련 병렬성을 가지며 성능이 비슷하며 효율적인 추론 $O(1)$ 을 달성하기 위해 아래와 같은 방법론들을 제시하였다.

3-1. Retention

본 논문에서는 Attention 메커니즘을 Retention 메커니즘으로 대체하였다.

본 논문에서의 Retention은 Parallel + Recurrent을 결합한 상태로 저자는 기존의 Retention의 수식을 변형하여 기존의 Recurrent를 Parallel하게 변경하였으며 이 둘을 결합한 Retention을 만들어 내었다.

Retention의 수식을 변형하는 과정은 아래와 같다.

전체적인 과정은 $v(n)$ -> $o(n)$ 으로 맵핑 시키는데 중점을 두게 된다.
주어진 X는 $X \in \mathbb{R}^{|x| \times d_{\text {model }}}$ 로 일련의 시퀀스가 입력된다.
이를 $v(n)=X_n \cdot \boldsymbol{w}_V$ 으로 투영하여 $v(n)$ 은 각각의 토큰을 의미한다.
$s_n=A s_{n-1}+K_n^{\top} v_n, \quad A \in \mathbb{R}^{d \times d}, K_n \in \mathbb{R}^{1 \times d}$ 이 수식에서는 $s_{n}$ 과 $s_{n-1}$ 그리고 $v(n)$ 을 보게 되면 결국 각 토큰이 순차적으로 다음 토큰을 계산할때 Autoregressive하게 입력되어 시퀀스 정보를 반복적으로 인코딩 한다.
다음으로 (1)의 계산식중 $o_n=Q_n s_n=\sum_{m=1}^n Q_n A^{n-m} K_m^{\top} v_m, \quad Q_n \in \mathbb{R}^{1 \times d}$ 를 보게 되면 이때의 $s_{n}$ 은 전체 토큰(시퀀스)의 $s_{n}$ 이다. 이는 풀어서 쓰게되면 결국 $Q_n\left[A\left(A s_{n-2}+K_{n-1}^{\top} V_{n-1}\right)+K_n^{\top} V_n\right]$ 형태로 나타나게 된다.
이후 $W_{Q}$ 와 $W_{K}$ 를 만들게 되는데 이는 각각 학습 가능한 매트릭스이다.
그리고 이떄 행렬 $A$ 를 대각선화 합니다. $A=\Lambda\left(\gamma e^{i \theta}\right) \Lambda^{-1}, \text { where } \gamma, \theta \in \mathbb{R}^d$
결국 그러면 $A^{n-m}$ = $\Lambda\left(\gamma e^{i \theta}\right)^{n-m} \Lambda^{-1}$ 을 얻어내게 됩니다.
$o_n=Q_n s_n=\sum_{m=1}^n Q_n A^{n-m} K_m^{\top} v_m, \quad Q_n \in \mathbb{R}^{1 \times d}$ 를 변환 행렬 $\Lambda$ 에 $W_{Q}$ , $W_{K}$ 를 흡수 시켜 다시 전개하게 되면 아래와 같은 식으로 변경할수 있습니다.

\begin{aligned} o_n & =\sum_{m=1}^n Q_n\left(\gamma e^{i \theta}\right)^{n-m} K_m^{\top} v_m \\ & =\sum_{m=1}^n\left(Q_n\left(\gamma e^{i \theta}\right)^n\right)\left(K_m\left(\gamma e^{i \theta}\right)^{-m}\right)^{\top} v_m \end{aligned}

이때 위 식의 $Q_n\left(\gamma e^{i \theta}\right)^n$ 과 $K_m\left(\gamma e^{i \theta}\right)^n$ 는 A length-extrapolatable transformer 논문에 따르면 $Xpos$ 라고 합니다. 이는 Transformer의 Position embedding으로 알려져 있다고 합니다.

논문에서는 이후 $γ$ 를 scalar 값으로 처리하여 식을 더욱 단순화 하였습니다. 이때 $†$ 는 켤레 전치(conjugate transpos)이며 최종적으로 교육할때는 쉽게 병렬화가 가능하다고 합니다.

\begin{aligned} o_n=\sum_{m=1}^n \gamma^{n-m}\left(Q_n e^{i n \theta}\right)\left(K_m e^{i m \theta}\right)^{\dagger} v_m \end{aligned}

요약하면 (1)과 같이 순환 모델링을 구성해서 (4)에서 병렬로 바꾸는 공식을 도출한 후 $v(n)$ 을 $o(n)$ 벡터로 간주하여 위와 같은 메커니즘을 얻게 됩니다.

저는 위 수식만으로 병렬화가 이해가 안되어서 병렬화는 아래에서 조금 더 자세히 알아보도록 하겠습니다.

3-2. Parallel Representation of Retention

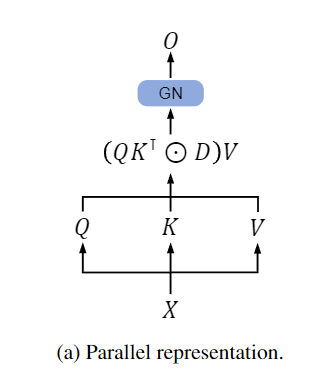
병렬화에 대해 조금 더 자세히 알아보면 위와 같은 그림이 나오게 되고 수식은 아래와 같습니다.

\begin{aligned} o_n=\sum_{m=1}^n \gamma^{n-m}\left(Q_n e^{i n \theta}\right)\left(K_m e^{i m \theta}\right)^{\dagger} v_m \end{aligned}

위 수식은 아래와 같이 정리할 수 있게 됩니다.

\begin{gathered} Q=\left(X W_Q\right) \odot \Theta, \quad K=\left(X W_K\right) \odot \bar{\Theta}, \quad V=X W_V \\ \Theta_n=e^{i n \theta}, \quad D_{n m}= \begin{cases}\gamma^{n-m}, & n \geq m \\ 0, & n<m\end{cases} \\ \text { Retention }(X)=\left(Q K^{\top} \odot D\right) V \end{gathered}

이떄 $\bar{\Theta}$ 는 $\Theta$ 의 켤례 복소수 이며 $D$ 는 $D ∈ R|x|×|x|$ 와 같습니다.

\quad D_{n m}= \begin{cases}\gamma^{n-m}, & n \geq m \\ 0, & n<m\end{cases}

이 $D$ 에 대해 저 자세히 알아보면 $D$ 는 상대적인 거리와 지수 감쇠(D is causal masking + decay matrix.)를 나타내게 되는데 결국 이 부분은 3-1.의 10.에서 나온 수식인

\begin{aligned} o_n=\sum_{m=1}^n \gamma^{n-m}\left(Q_n e^{i n \theta}\right)\left(K_m e^{i m \theta}\right)^{\dagger} v_m \end{aligned}

중에서 $\gamma^{n-m}$ 를 나타내게 됩니다. 이를 코드로 표현하면 아래와 같습니다.

gamma = 0.9
exponent = [[0, 0, 0, 0],
            [1, 0, 0, 0],
            [2, 1, 0, 0],
            [3, 2, 1, 0]]

D = tril(gamma**exponent)
# [[1.,     0.,     0.,     0.],
#  [0.9000, 1.,     0.,     0.],
#  [0.8100, 0.9000, 1.,     0.],
#  [0.7290, 0.8100, 0.9000, 1.]])

이를 통해 $\text { Retention }(X)=\left(Q K^{\top} \odot D\right) V$ 가 병렬적으로 처리가 가능하게끔 됩니다.
이를 pseudocode로 나타내면 아래와 같습니다.

3-3. The Recurrent Representation of Retention

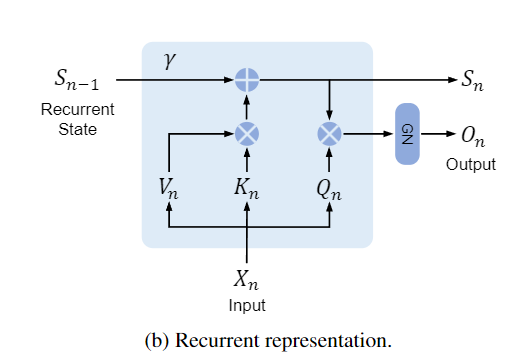
\begin{gathered} Q=\left(X W_Q\right) \odot \Theta, \quad K=\left(X W_K\right) \odot \bar{\Theta}, \quad V=X W_V \\ \Theta_n=e^{i n \theta}, \quad D_{n m}= \begin{cases}\gamma^{n-m}, & n \geq m \\ 0, & n<m\end{cases} \\ \text { Retention }(X)=\left(Q K^{\top} \odot D\right) V \end{gathered}

\begin{aligned} & S_n=\gamma S_{n-1}+K_n^{\top} V_n \\ & \operatorname{Retention}\left(X_n\right)=Q_n S_n, \quad n=1, \cdots,|x| \end{aligned}

$D$ 를 제외하면 위와 같은 수식을 다시 Recurrent 형태로도 나타낼수 있습니다. 그럴 경우 아래와 같은 식이 나오게 됩니다.
이는 $s_n=A s_{n-1}+K_n^{\top} v_n$ 3-1의 (1)과 유사합니다. 기존의 식을 가져올 경우 이러한 수식이 나오게 됩니다.
기존의 병렬처리를 인퍼런스 시에는 포기하며 이러한 방식으로 인퍼런스를 하게 되어 추론 시 속도에 유리합니다. 아마 제 생각에는 논문에 직접적으로 나와있지 않지만 $\gamma$ 를 $D$ 라는 마스크 행렬을 사용하지 않아 기존처럼 순차적으로 전환한거 같습니다.

\begin{gathered} S_n=\sum_{i=1}^n \gamma^{n-i} K_i^T V_i \\ \operatorname{Retention}\left(X_n\right)=Q_n \sum_{i=1}^n \gamma^{n-i} K_i^T V_i \end{gathered}

https://medium.com/@choisehyun98/the-rise-of-rnn-review-of-retentive-network-a080a9a1ad1d 링크에서 논문에서는 증명하진 않았지만 위 결과적으로 Recurrent와 Parallel는 완벽히 동일 수식이라고 비공식으로 위 수식으로 예를 들어 설명하였습니다.

결론적으로 이를 pseudocode로 나타내면 아래와 같습니다.

3-4. Chunkwise Recurrent Representation of Retention

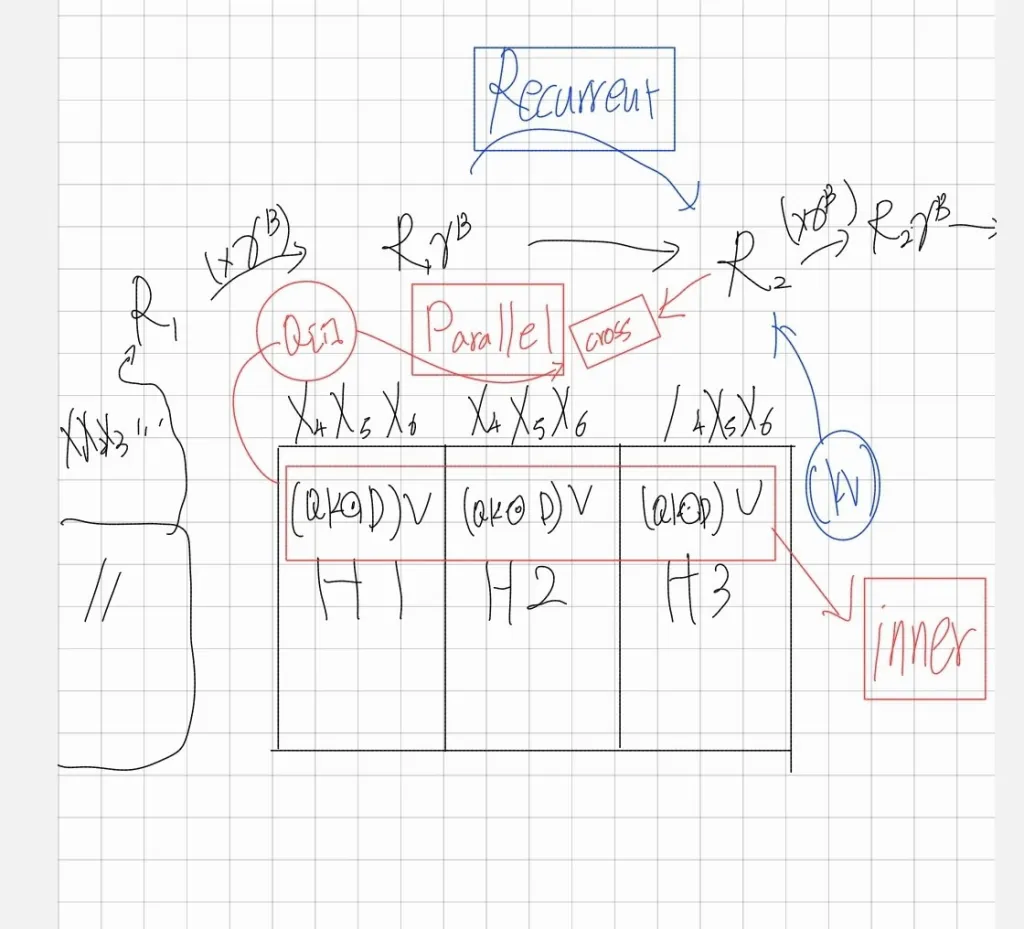
출처 : LATTE TIMES

\begin{aligned} & Q_{[i]}=Q_{B i: B(i+1)}, \quad K_{[i]}=K_{B i: B(i+1)}, \quad V_{[i]}=V_{B i: B(i+1)} \\ & R_i=K_{[i]}^{\top} V_{[i]}+\gamma^B R_{i-1} \\ & \operatorname{Retention}\left(X_{[i]}\right)= \underbrace{\left(Q_{[i]} K_{[i]}^{\top} \odot D\right) V_{[i]}}_{\text {Inner-Chunk }}+\underbrace{\left(Q_{[i]} R_{i-1}\right) \odot \xi}_{\text {Cross-Chunk }}, \quad \xi_{i j}=\gamma^{i+1} \end{aligned}

where $[i]$ indicates the $i$ -th chunk, i.e., $x_{[i]}=\left[x_{(i-1) B+1}, \cdots, x_{i B}\right]$ .
B는 청크의 길이 입니다.

위 수식은 Recurrent와 Parallel를 결합한 방식 하이브리드 방식입니다. 입력 시퀀스를 청크 단위로 나누어 각 청크(Inner-Chunk) 내부의 연산은 Parallel하게 진행하며 과거의 청크(Cross-Chunk)를 Recurrent하게 참조하여 계산하게 됩니다.
이를 pseudocode로 나타내면 아래와 같습니다.

3-5. Gated Multi-Scale Retention

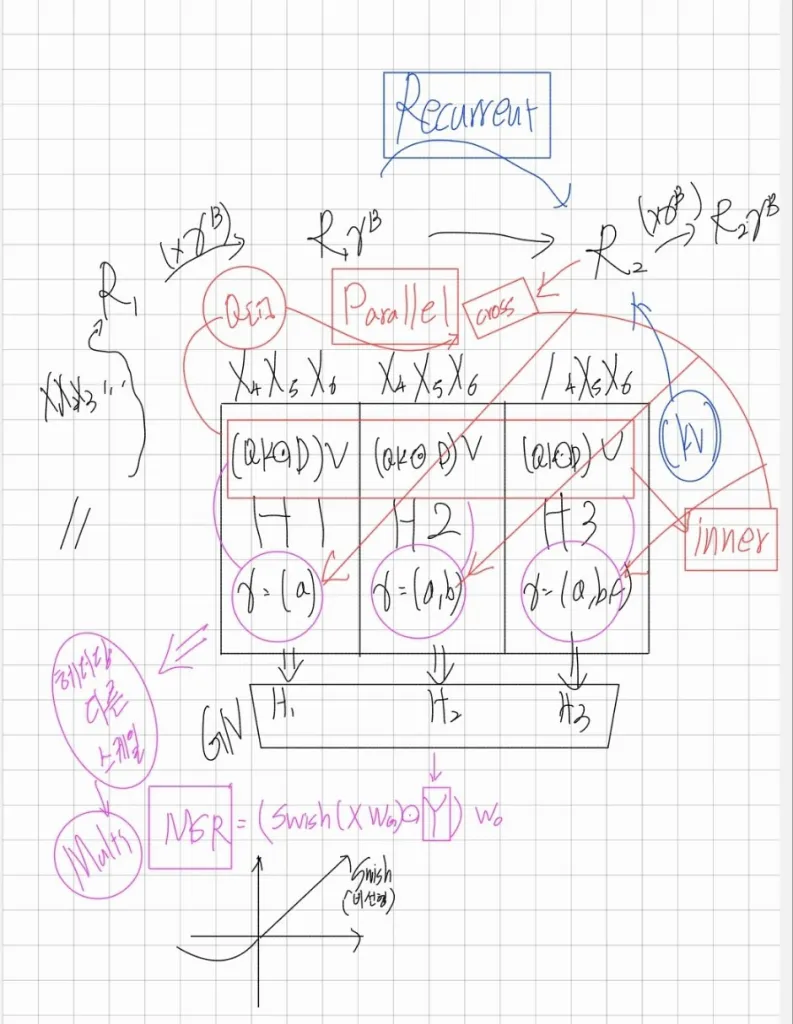
출처 : LATTE TIMES

\begin{aligned} & \gamma=1-2^{-5-\operatorname{arange}(0, h)} \in \mathbb{R}^h \\ & \operatorname{head}_i=\operatorname{Retention}\left(X, \gamma_i\right) \\ & Y=\operatorname{GroupNorm}_h\left(\operatorname{Concat}\left(\operatorname{head}_1, \cdots, \operatorname{head}_h\right)\right) \\ & \operatorname{MSR}(X)=\left(\operatorname{swish}\left(X W_G\right) \odot Y\right) W_O \\ & \end{aligned}

위 수식은 각 레이어에 즉 청크마다의 다른 헤더( $γ$ )를 적용하는 것입니다. 한개의 청크를 헤드로 나눈다는 점입니다.(멀티 헤드 어텐션과 유사하게 다양성을 높혀준다고 합니다.)
각 헤더당 다른 $\gamma$ 와 서로 다른 $W_{Q},W_{K},W_{V}$ 를 적용하여 각 $head_{i}$ 를 구하며 이를 Concat 시킨후 GropNorm을 적용시켜 줍니다.헤드가 여러 $\gamma$ 를 통해 분산 통계가 달라짐으로 GropNorm은 각 헤드의 출력을 정규화 해줍니다.
이때 $W_{G},W_{O}$ 는 학습 가능한 파라미터이며 또한 비선형성을 증가시키기 위해 swisch 함수가 추가 되었습니다.

3-6. Model Architecture

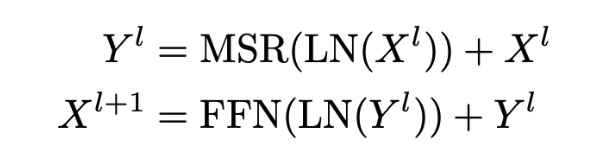
각 RetNet의 레이어는 위처럼 구성되어 있습니다. MultiScaleRetention과 FeedForwardNetwork의 반복으로 구성되있으며 FFN은 2개의 MLP 레이어가 사용되며 트랜스포머와 유사합니다.
hiddin dim size = 2 x embedding size, gelu이며 결국 MulitHeadAttention을 MultiScaleRetention로 대체하면 됩니다.

3-7. Benefits of MSR Training

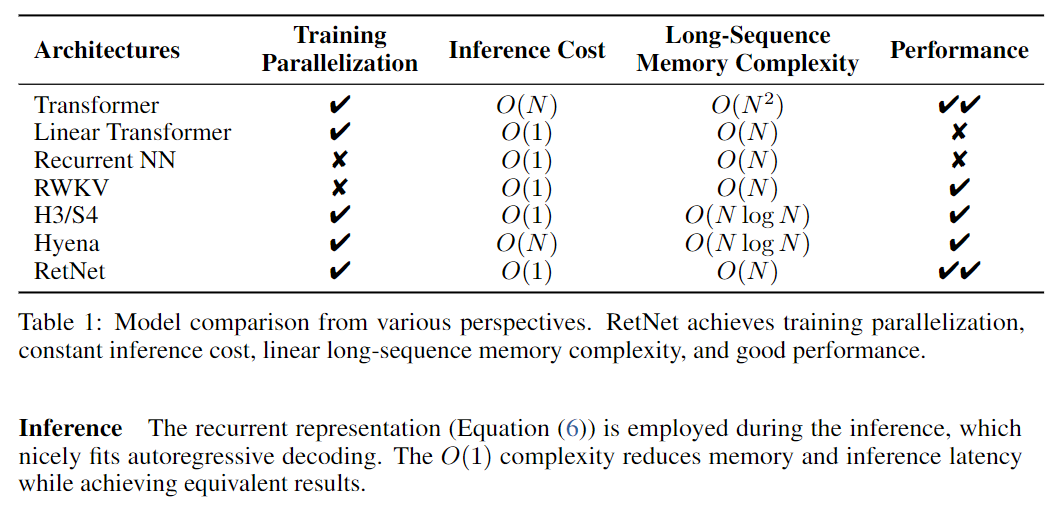
모든 부분을 충족하는 효과를 얻어내었다. 또한 7B 모델의 8k의 시퀀스의 경우 RetNet은 key-value가 있는 Transforemr보다 8.4배 빠르게 디코딩하며 70%의 메모리를 절약하였다. 또한 훈련중에는 25~50%의 메모리를 절약하고 7배의 가속을 달성하였다고 한다.

✨Contribution

병렬 형식: 빠른 교육용
반복 형식: 빠른 추론(토큰)을 위해
Chunkwise recurrent form: 매우 긴 시퀀스에 대한 빠른 교육용
모든 것을 달성한 모델로써 병렬처리와 인퍼런스의 속도 및 훈련, 성능을 고려하였으며 병렬과 순차적인 방법의 절충안이다.

4. 실험 및 결과

Language modeling을 통하여 평가하였으며 LM, zero/few-shot learing을 평가하며 훈련과 추론의 경우 속도,메모리,지연시간을 비교한다. 이때 추론같은 경우는 3-3의 Recurrent을 사용하였다고 한다.

4-1. setup

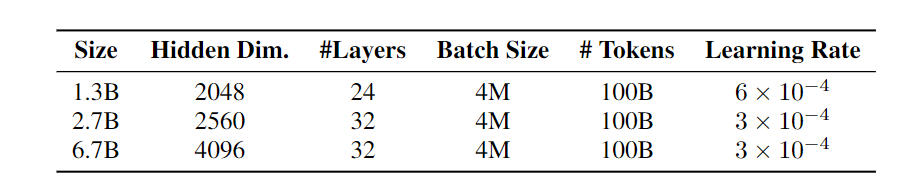
비교를 위해 총 3가지의 모델을 선정하였으며 파라미터는 위와 동일하며 Transformer 또한 비슷한 크기의 모델을 구성하였다.

4-2. Language Modeling

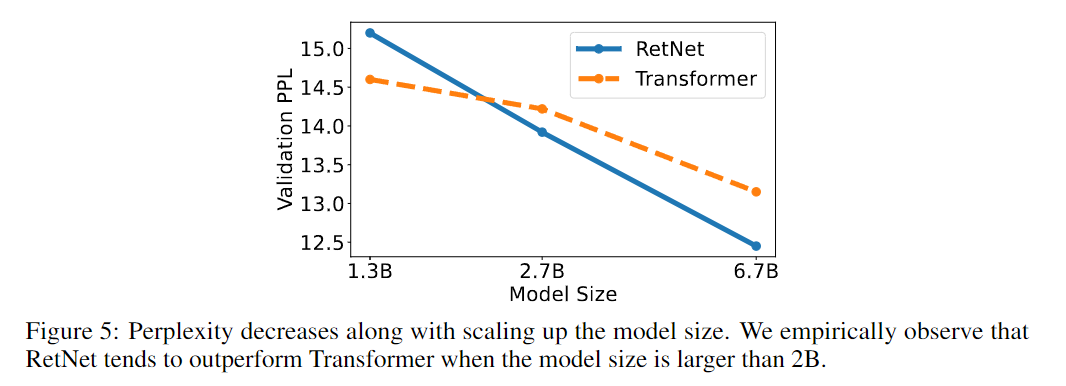
모델의 크기가 2B이상 부터는 Transformer을 이기는 경향을 보여준다. 추가로 시작 토큰을 삽입할 경우 훈련이 보다 안정적으로 진행된다고 한다.

4-3. Zero-Shot and Few-Shot Evaluation on Downstream Tasks

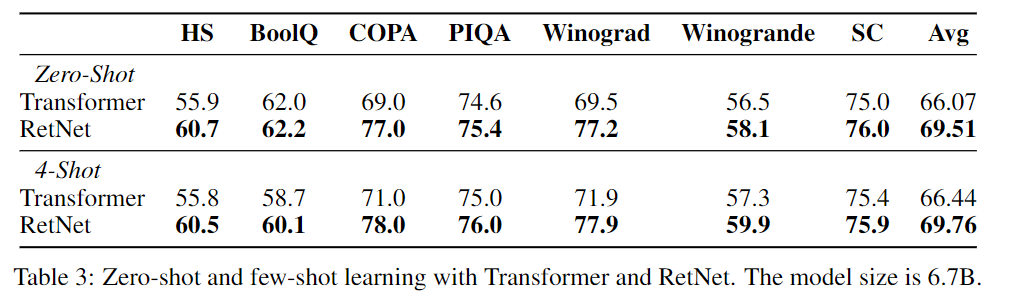
6.7B의 모델을 사용하여 zero-shor과 4-shot learing을 학습하였다. Language Modeling을 통해 평가하였으며 4-2.의 그래프 처럼 모든 부분에서 앞선 모습을 보여주었다.

4-4. Training Cost

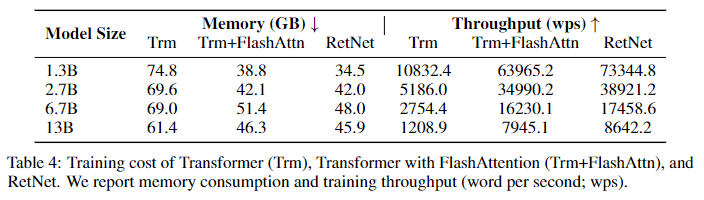
이번 실험헤서는 Transformer와 FlashAttn을 사용한 Transformer와 비교하였다. 비교적 FlashAttn보다는 훈련속도에서 밀리는 반면 메모리 측면에서는 조금 더 나은 모습을 보여주었다. 하지만 저자는 FlashAttn의 경우 Nvidia A100-80G에 최적화 되어 있어 동일하게 사용하였다는 점과 RetNet AMD MI200을 사용하며 아직 Kennel fusion과 같은 구현을 통해 보다 아직 잠재력이 있다고 설명한다.

4-5. Inference Cost

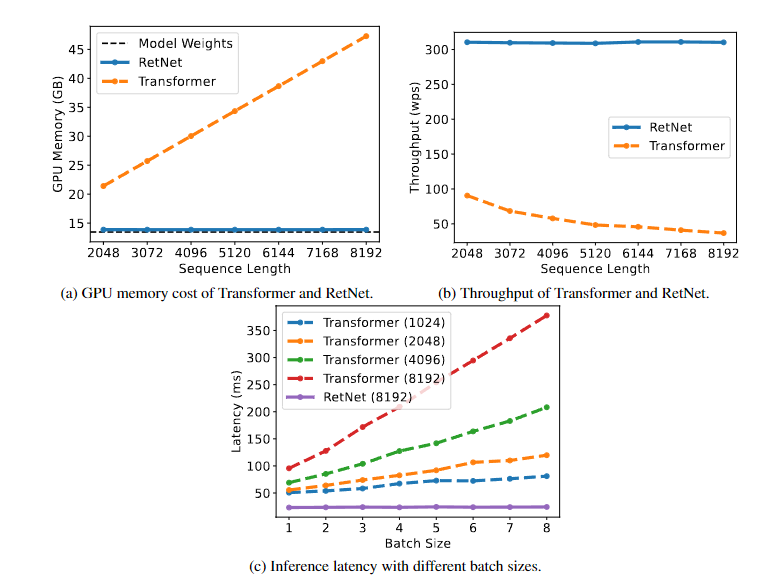
(a) TransForemr의 같은 경우 Sequence Length에 GPU Memory따라 선형적 $O(N)$ 으로 증가하는 반면 RetNet은 $O(1)$ 이라 증가하지 않는다.

(b) 처리량의 경우 디코딩에 길이에 따라 Transformer는 속도가 점차 감소하게 되지만 RetNet은 무관하게 일정하다.

(c) 지연시간은 Transformer의 경우 배치 크기가 늘어날 수록 늘어나는 경향을 보였고 입력이 길수록 지연시간은 빠르게 증가한다. 하지만 RetNet은 아양한 배치크기 그리고 입력 길이를 조절하여도 동일하게 유지되었다.

4-6. Comparison with Transformer Variants

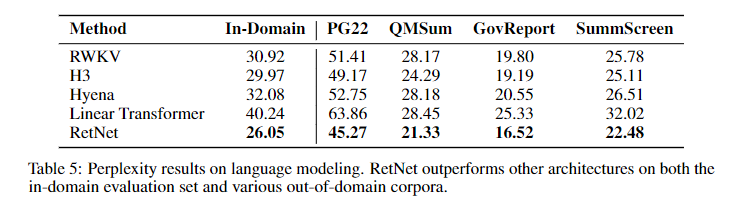
다른 다양한 Transformer와 비교하여도 압도적인 성능을 달성하며 입증하였다.

4-7. Ablation Studies

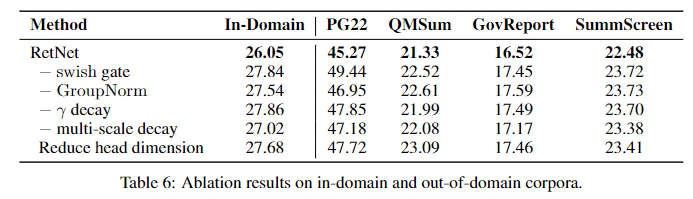
각각의 설계를 제한하고 실험을 하였다. 결국 swish와 GroupNorm은 최종 성능을 향샹시키며 필수적인 요소라는 점을 증명하였다.
다른 마라미터 또한 deacy를 변형시켰더니 최종 모델보다 성능이 감소한다는 점을 볼 수 있다.

5. Conclusion

병렬,순환,청크 단위로 다양한 표현을 가능하게끔 하는 RetNet을 제안하였다. 다른 Transformer 모델들 보다도 동일 파라미터에서 높은 성능을 보였으며 특히 추론적인 부분에서 성능을 유지하며 $O(1)$ 은 기존의 패러다임을 바꾸었다고 생각된다.
추후 아직 초기모델로써 다양한 변형과 모델 크기를 생각하여 대규모 언어 모델을 구성할 수 있으며 추론시간의 장점으로 엣지 디바이스에서의 모델에서 이점이 존재할 수 있다는 가능성을 시사하였다.

6. 회고

언어 모델링 부분에서는 물론 Transformer을 능가한다 하더라도. Transformer의 진짜 힘은 다양한 정보들의 관계성을 캡쳐한다는 부분이다. 그래서 Transformer가 다른 대부분의 Domain과 Task에 사용되는 것이며 Image Bind 그리고 Meta-Transformer가 나오며 멀티모달을 가능하게끔 해준것이다. 하지만 아직 이 논문에서는 그런 MSR이 Attention처럼 다른 정보들을 캡쳐한다는 정보는 없으며 어떻게 대체하는지에 대한 설명이 부족하며 LM모델로써의 Transformer와 비교를 한다. 이는 NLP에서는 Transformer를 능가한다하더라도 딥러닝에서 Transforemer을 대체할 것이라는 생각은 아직 부정적인 생각이다. 그래도 초기 모델로 이 정도의 성능과 추론 속도는 놀라울 정도이다.