MLP로 Mnist 분류하기

위와 같은 데이터셋으로 0~9까지의 글씨 사진과 라벨로 0~9까지의 라벨이 그려져 있음

model

class MnistModel(nn.Module):
    def __init__(self):
        super(MnistModel, self).__init__()
        self.fc1 = nn.Linear(28 * 28, 512)
        self.fc2 == nn.Linear(512,10)
    def forward(self, x):
        x = x.view(-1,28*28)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        return F.log_softmax(x)
    
model = MnistModel()
model

위와 같은 모델을 구성할 경우 mnist의 이미지 shape (28,28,1)이 들어올때 이를 view함수로 먼저 (-1,28*28)로 변환 시켜주고
Linear층을 통하여 선형결합을 해주며 이후 활성화 함수 RelU를 통과시킨다.
최종적으로 F.log_softmax를 통해 합이 1인 10개의 확률 값으로 변환시켜 loists을 얻어낸다.

train

model.train()
train_loss = []
train_accu = []
i = 0
for epoch in range(15):
    for data, target in train_loader:
        data, target = Variable(data), Variable(target)
        optimizer.zero_grad()
        output = model(data)#(10)
        loss = F.nll_loss(output, target)#(10,)(10,)
        loss.backward()    # calc gradients
        train_loss.append(loss.item())
        optimizer.step()   # update gradients
        prediction = output.data.max(1)[1]   # first column has actual prob.
        accuracy = prediction.eq(target.data).sum()/batch_size*100
        train_accu.append(accuracy)
        if i % 1000 == 0:
            print('Train Step: {}\tLoss: {:.3f}\tAccuracy: {:.3f}'.format(i, loss.item(), accuracy))
        i += 1

훈련코드는 위와 같으며 단순하게 model에 data를 넣고 통과시키고 loss로 backward() 시킨후 옵티마이저를 업데이트 시킨다.

CNN으로 Mnist분류하기

class MnistModel(nn.Module):
    def __init__(self):
        super(MnistModel, self).__init__()
        self.layer1 = torch.nn.Sequential(
        torch.nn.Conv2d(1,32,kernel_size=3,stride=1,padding=1),
        torch.nn.Relu()
        torch.nn.MaxPool2d(kernel_size=2,stride=2)
        )
        self.layer2 = torch.nn.Sequential(
        torch.nn.Conv2d(32,64,kernel_size=3,stride=1,padding=1),
        torch.nn.Relu()
        torch.nn.MaxPool2d(kernel_size=2,stride=2)
        )
        self.fc = torch.nn.Linear(7 * 7 * 64, 10, bias=True)
    def forward(self, x):
        out = self.layer1(x) #(?,14,14,32)
        out = self.layer2(out) #(?,7,7,64)
        out = out.view(out.size(0), -1)# (7*7*64,10)
        out = F.log_softmax(self.fc(out))
    
model = MnistModel()
model

위와 같은 모델 구성시 self.layer1을 통과 할 경우 이미지의 크기가 (batch_size,14,14,32)가 되며 두번째로 self.layer2를 통과시 이미지의 크기는 (batch_size,7,7,64)가 되고 이를 view함수를 통해 (batch_size,-1)을 해주어 flatten시켜준다 최종적으로 Lineal층을 통과시켜 10개의 값으로 바꾸어 준다. 훈련 코드는 위와 동일하다.

Optimization

Cross validation

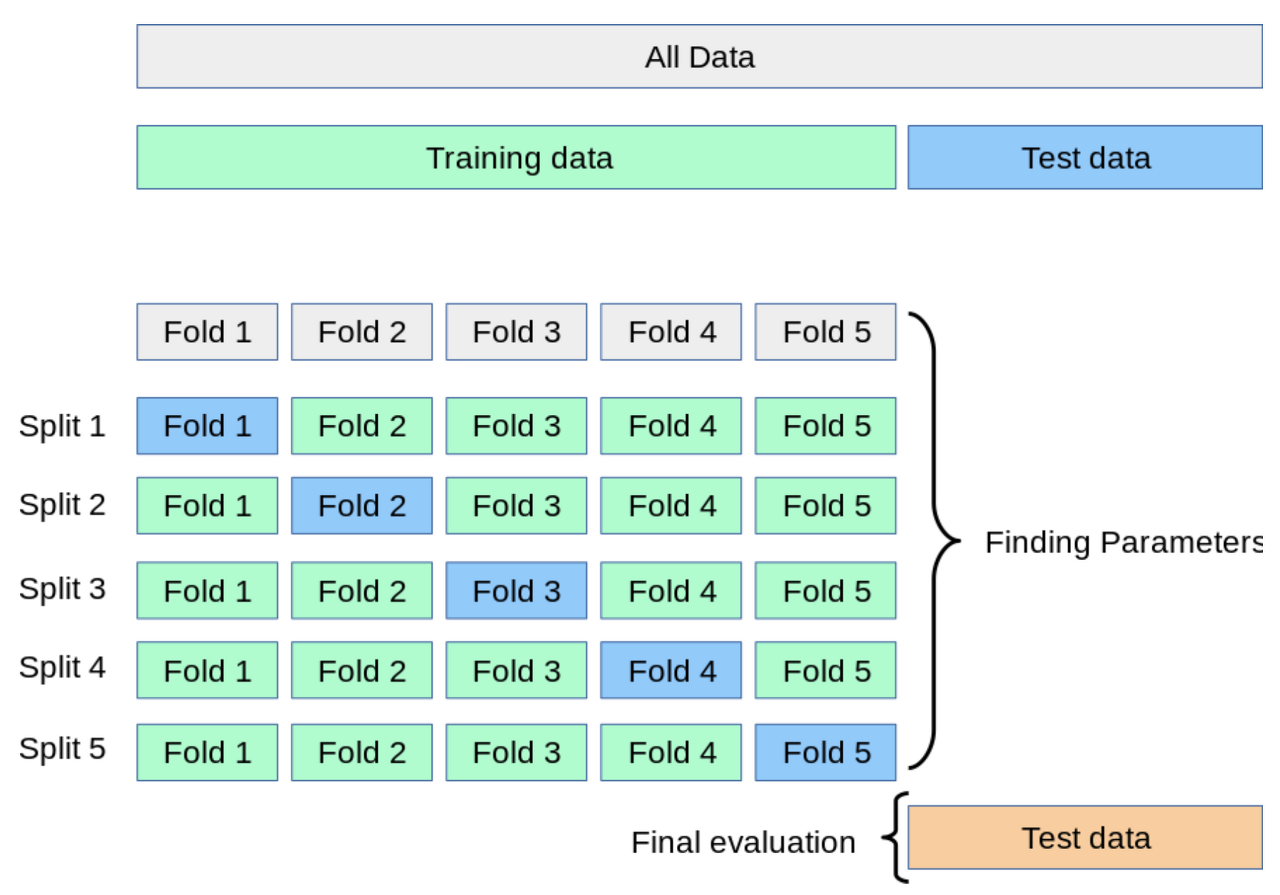
만약 data의 train set을 train,val로 나누지 않으면 train으로 훈련시키고 test로 검증할것이다. 이렇게 되면 우리가 만든 모델은 test에만 잘 동작하는 모델이 되어 test set에 과적합하게 된다. 이를 해결하고자 cross validation(교차검증)을 사용한다.
순서는 아래와 같다

1. 전체 데이터셋을 Training Set과 Test Set으로 나눈다.
2. Training Set를 Traing Set + Validation Set으로 사용하기 위해 k개의 폴드로 나눈다.
3. 첫 번째 폴드를 Validation Set으로 사용하고 나머지 폴드들을 Training Set으로 사용한다.
4. 모델을 Training한 뒤, 첫 번 째 Validation Set으로 평가한다.
5. 차례대로 다음 폴드를 Validation Set으로 사용하며 3번을 반복한다.
6. 총 k 개의 성능 결과가 나오며, 이 k개의 평균을 해당 학습 모델의 성능이라고 한다.

Bootstrapping

Bagging

단순하게 학습 데이터가 100개가 있으면 이중 80개씩을 랜덤하게 뽑아 모델을 만들고 이것을 n회 반복후 평균내어 최종모델을 만든다.
평균도 있고 max값만 뽑는것도 존재한다.(앙상블)

Boosting

간단한 모델을 학습 후 잘 예측하지 못하는 데이터에 대해서 모델을 새로 만든 후 이것을 잘 분류하는 모델을 훈련시켜 최종적으로 모델을 모두 합친다.

Gradient Descent Methods

SGD

가장 기본적은 Gradient Descent 방법으로 수식은 아래와 같다. 단순하게 기존 가중치에서 그레디언트 * lr 을 뺴준다
단점으로 lr을 잡아주는게 어렵다.

Momentum

더 빠르게 수렴하는 옵티마이저인데 기존의 SGD에서 관성을 추가한것이라고 볼 수 있다. β인 하이퍼 파라미터(관성)가 들어간다.
결국 Gradient가 많이 왔다갔다해도 일관성을 어느정도는 유지시켜준다.

Nesterov Accelerate

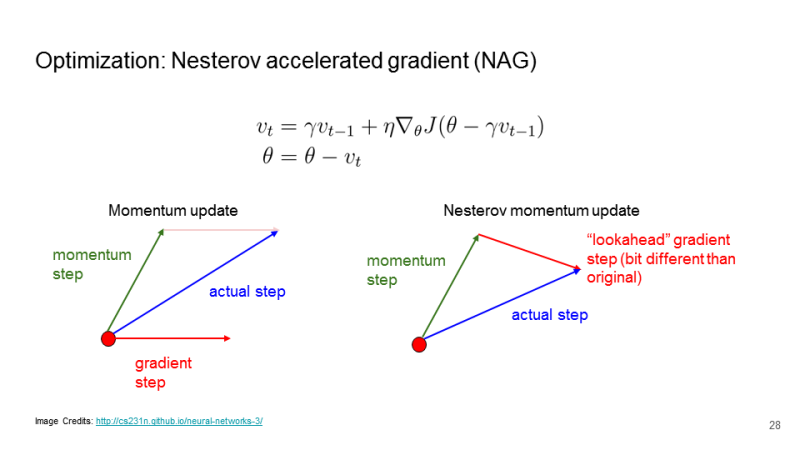
모멘텀 스텝에 의해서 움직인 상태에서의 기울기 상태를 계산하여 이동을 하는 것이다. 로컬 미니멈으로 더 잘 수렴하는 효과가 있다.

Adagrad

파라미터의 변화값 $G_{t}$ 저장 후 확인하고 많이 변한 파라미터에 대해선 적게 변화시키고 조금 변화시킨 파라미터는 많이 변화 시킨다. $G_{t}$가 점점 커지는데 분모 텀에 있으므로 점점 Gradient의 변화량이 적어진다.

Adadelta

시간이란 개념을 도입(윈도우 사이즈) 윈도우 사이즈를 주어 그 윈도우 사이즈 내의 변화량만 가지고 변화 시킨다.
문제점으로 윈도우 사이즈가 100일 경우 이전 100개 동안의 $G$라는 정보를 가지고 있어야 한다. 근데 모델이 클 경우 모델의 파라미터수가 1억이면 1억 * 100개의 기록이 필요한것이다. 다행히 지수 평균 이동으로 어느정도 완화한다.

RMSprop

AdaGrad에서 학습이 안되는 문제에서 하이퍼 파라미터 $β$가 추가됐다.
변화량이 더 클수록 학습률이 작아져서 조기 종료되는 문제를 해결하기 위해 학습률 크기를 비율로 조정할 수 있도록 제안된 방법입니다.
RMSProp은 최근 경로의 곡면 변화량을 측정하기 위해 지수가중이동평균을 사용한다.

Adam

Adam은 Momentum과 RMSProp의 장점을 결합한 알고리즘이다. 모르겠으면 그냥 쓰는게 좋다.
지수평균이동과 관성을 같이 이용한다. 잘 모르겠으면 쓰면된다.

Regularization

Early stopping

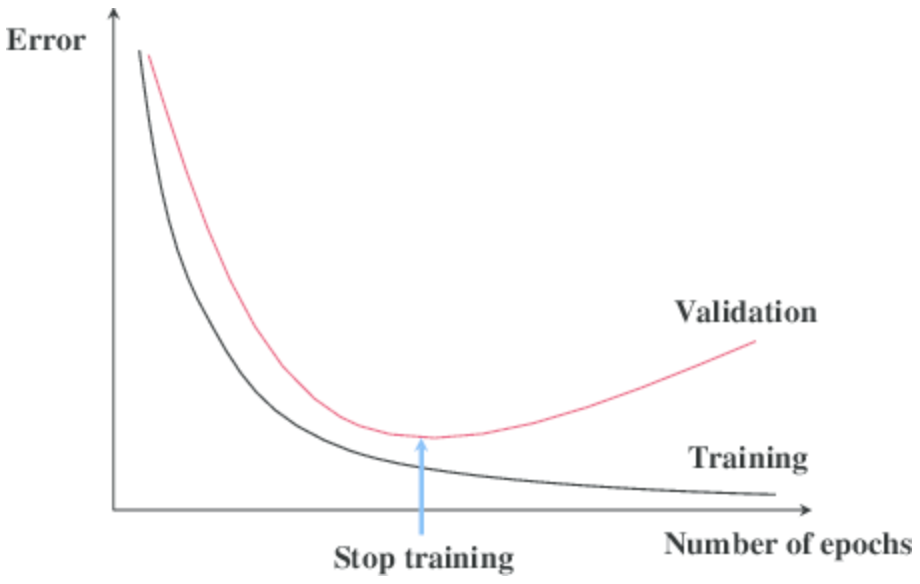
acc나 loss를 기준으로 어느 시점부터 loss가 커지기 시작하거나 acc가 감소하는 시점에 학습을 중단 시킨다.

Parameter Norm Penalty

우리의 모델 f(x)에 weight decay나 l1 l2 규제를 가하여 우리의 모델 f(x)가 좀 더 부드럽게 한다.

Data augmentation

데이터 자체에 변형을 가하여 데이터의 다양성을 추가한다. 일반적으로 rotaion, resize, crop등의 파이토치에서 지원해주는 기본 기법이 있으며 아래와 같은 다양한 augmentataion도 있다.

Noise Robustness

일반적으로 입력에 Noise를 주거나 가중치에 Noise를 줄경우 학습이 잘되는 경향이 존재한다.

Label Smoothing

일반화를 높여주는 기법으로 일반적인 분류문제는 ont-hot으로 이루어져 있는데 이를 hard-target이라고 부른다 이를 [0,1,0,0]으로 이루어진것을 [0.025,0.925,0.025,.0.025]식으로 변경하여 soft target으로 만들어 학습에 사용한다. 이럴경우 분류 문제의 이미지 공간속의 분류 기준을 좀 더 부드럽게 만들어준다.

Batch Normalization

이는 배치단위로 데이터의 정규화를 수행한다. Internal Covariance Shift를 줄인다고 나와있다.