
LSTM으로 Mnsit 분류하기

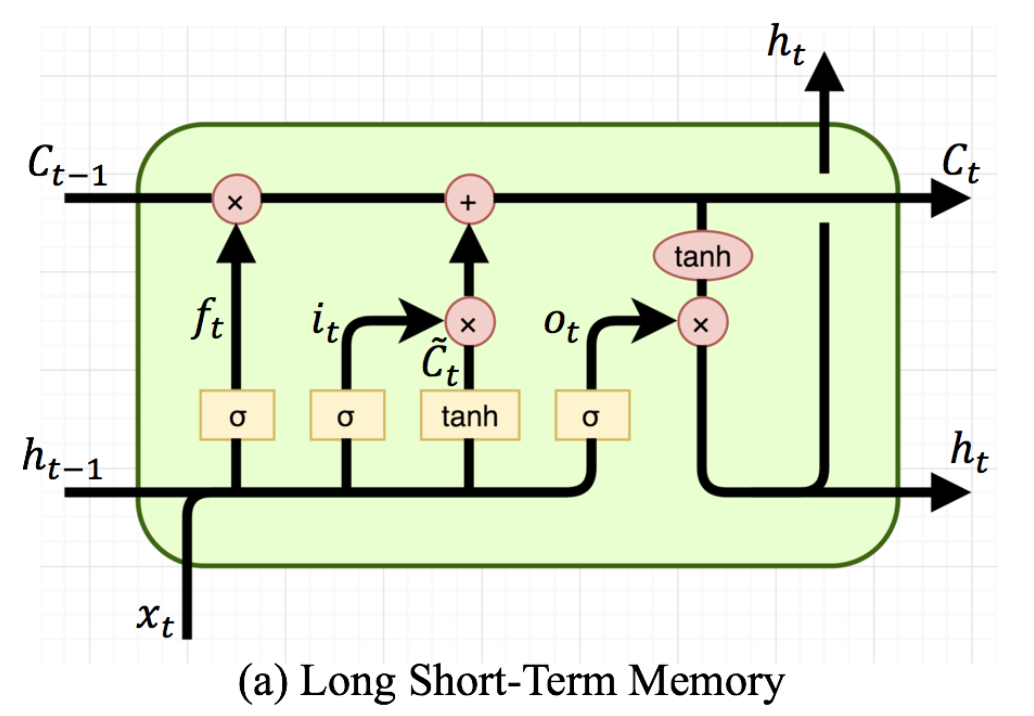
시퀀스 모델인 LSTM으로 Mnist를 분류 해보자
model
class RecurrentNeuralNetworkClass(nn.Module):
def __init__(self,name='rnn',xdim=28,hdim=256,ydim=10,n_layer=3):
super(RecurrentNeuralNetworkClass,self).__init__()
self.name = name
self.xdim = xdim
self.hdim = hdim
self.ydim = ydim
self.n_layer = n_layer # K
self.rnn = nn.LSTM(
input_size=self.xdim,hidden_size=self.hdim,num_layers=self.n_layer,batch_first=True)
self.lin = nn.Linear(self.hdim,self.ydim)
def forward(self,x):
# Set initial hidden and cell states
h0 = torch.zeros(
self.n_layer, x.size(0), self.hdim
).to(device)
c0 = torch.zeros(
self.n_layer, x.size(0), self.hdim
).to(device)
# RNN
rnn_out,(hn,cn) = self.rnn(x, (h0,c0))
# x:[N x L x Q] => rnn_out:[N x L x D]
# Linear
out = self.lin(
rnn_out[:, -1, :]
).view([-1,self.ydim])
return out
R = RecurrentNeuralNetworkClass(
name='rnn',xdim=28,hdim=256,ydim=10,n_layer=2).to(device)
loss = nn.CrossEntropyLoss()
optm = optim.Adam(R.parameters(),lr=1e-3)
print ("Done.")우선 LSTM의 인풋은 총 3개이다 cell state와 h-1 state 이때 배치별로 처음 데이터가 들어올경우 t-1의 cell state와 h-1 state가 없음으로 단순히 torch.zeros를 통해 만들어주고 이후 LSTM에 데이터(x)와 h0,c0를 함께 입력으로 넣어준다 이에 대한 아output은 (batchsize,token,hdim)으로 shape이 나오게 되고 이를 linear층을 통과시키는데 token과 hdim의 차원을 합치고 Linear(token*hdim,label)로 통과시켜 최종적인 분류를 수행하게 된다.
가정
내 생각엔 처음 LSTM에서 각 토큰의 hdim끼리 연산을 진행한후 Linear에서는 토큰끼리의 연산까지 더하여 진행되는것같다.
즉 mnist데이터를 시퀀스로 보게되면 각 행은 토큰이 되고 각 행의 열은 hdim이 되는것이다.
Transformer
Transformer의 핵심 기술인 Self attention과 Multi-head attention만 기술하도록 하겠다.
우선 Attention의 수식은 아래와 같다.
는 물어보는 주체이고 는 대상 는 그에 대한 그냥 값이라고 보면된다.
이때 랑의 행렬곱을 로 나누어 주게 되고 이를 함수 통과후 와 곱해주는 과정을 진행하게 된다.
self_attention
n_batch,d_K,d_V = 3,128,256
n_Q,n_K,n_V = 30,50,50
Q = torch.rand(n_batch,n_Q,d_K) #(3,30,128)
K = torch.rand(n_batch,n_K,d_K) #(3,50,128)
V = torch.rand(n_batch,n_V,d_V) #(3,50,256)
sqrt_d_K = K.size()[-1]
scores = Q.matmul(K.transpose(-2,-1))/np.sqrt(sqrt_d_K) # (3,30,50)
attention = F.softmax(scores,dim=-1) #(3,30,50)
out = attention.matmul(V)#(3,30,256)단순하게 위 수식 그대로 진행하게 된다.
Multi-head attention
self_attention에서 마지막 차원을 헤드의 갯수로 나눠 진행한다. 헤드가 8개인 경우이다.
n_batch,d_K,d_V = 3,128,128
n_Q,n_K,n_V = 30,30,30
Q = torch.rand(n_batch,n_Q,d_K) #(3,30,128)
K = torch.rand(n_batch,n_K,d_K) #(3,30,128)
V = torch.rand(n_batch,n_V,d_V) #(3,30,128)
Q_split = Q.view(n_batch,-1,8,128//8).permute(0,2,1,3) #(batch,n_head,n_Q,d_head) (3,8,30,16)
K_split = K.view(n_batch,-1,8,128//8).permute(0,2,1,3) #(batch,n_head,n_Q,d_head) (3,8,30,16)
V_split = V.view(n_batch,-1,8,128//8).permute(0,2,1,3) #(batch,n_head,n_Q,d_head) (3,8,30,16)
sqrt_d_K = K.size()[-1]
scores = torch.matmul(Q_split,K_split.permute(0,1,3,2))/np.sqrt(sqrt_d_K) # (3,8,30,30)
attention = F.softmax(scores,dim=-1) #(3,8,30,30)
out = torch.matmul(attention,V)#(3,8,30,16)
out = out.permute(0,2,1,3).contiguous() # (3,30,8,16)
out = out.view(n_batch,-1,128) # (3,30,128)실제 구현엔 dropout과 각종 Linear층이 포함되있다.
실제 attention에서 학습은 Linear층에서 Q와K의 관계를 구하는것이 학습으로 이루어진다.
회고
실제로 Transformer에 대해 구현하면 엄청난 코드가 필요함으로 self attention과 multi-head attention만 구현한 모습이다.
그래도 Transformer의 핵심 기술에 대해 제대로 배울 수 있어서 좋은거 같다. 비록 내용은 짧지만 트랜스포머는 나중에 다시 한번 다룰 예정이다. 오랜만에 차원을 가지고 노니까 머리가 피곤하다.

