Introduction
3d reconstruction을 할 때 SDF학습을 진행합니다. sdf학습을 할 때 이 물체가 어떻게 생겼는지를
미리 안다면 훨씬 학습이 효율적으로 진행되지 않을까요? 이러한 생각에서 시작한 autoSDF를 소개하겠습니다. 우리가 책상을 절반만 봤을 때 이것이 책상이라는 사전 정보가 있다면 우리는 책상의 전체를 상상할 수 있습니다.
이것처럼 prior 정보를 활용하여 sdf학습을 진행하려고 합니다.
이 prior를 학습할 때 continuous하고 high-dimensional 표현에서 진행한다면 계산량이 너무 많기 때문에 유용하지 않을 것입니다. 그래서 이 논문은 discrete한 표현을 사용하려고 합니다.
Related Work
보통 related work는 소개를 안하는데 이것은 모르면 논문을 읽지 못하여 기록을 해놓습니다.
Autogressive Modeling
(논문 내용 이외 조사한 내용도 기록하였습니다.)
Autogressive model은 시계열 데이터나 구조화된 데이터를 다룰 때 사용하는 통계 모델로, 현재 시점의 값을 이전 시점의 값들에 의존하여 예측하는 방식입니다.
joint distribution을 conditional distribution의 곱으로 나타낸다면 이러한 modeling으로 볼 수 있습니다. P(x) = ∏p(Xi|X<i) 이렇게 나타나면 이전 시점의 data로 현재 시점을 예측한다고 나타낼 수 있습니다.
이러한 구조를 사용하는게 transformer인데 이 모델은 크기가 너무 크기 때문에 data를 low resolution으로 바꿔 넣습니다. latent representation은 VQ-VAE를 활용하여 나타냅니다.
VQ-VAE는 데이터에서 잠재표현을 나타내주는 unsupervised-learning model로 이산적인 잠재공간을 학습합니다. 이산적으로 나타내진 코드북으로 데이터를 나타내는 것이라고 생각하시면 됩니다.
Discretized Latent Space for 3D Shapes
Encoder 에 data를 넣어 low dimension의 data를 만들어줍니다. 그것을 VQ-VAE에 넣어 latent representation을 해줍니다. VQ-VAE를 쓰기 때문에 Latent space는 discrete하다고 얘기할 수 있습니다.
만약 부분만 보고 encoder에 넣는다면 전체 모양을 나타내는 잠재벡터를 만들 수가 없습니다.
전체를 encoder에 넣는 것과 부분만 encoder에 넣으면 다른 결과값이 나오기 떄문입니다.
이를 해결하기 위해서 이 논문에서는 Patch-wise Encoding VQ-VAE 또는 P-VQ-VAE를 사용합니다.
이것은 encoding을 전체를 한 번에 하지 않고 잘라서 하기 때문에 아까의 단점을 해결할 수 있습니다.
Non-Sequential Autogressive Modeling
latent space Z는 original 3d shape을 나타내는 3d grid token입니다.
P(x) = ∏p(Xi|X<i) 이 상태에서 순서대로 이전 latent를 반영한다면 이것이 불가능한 상황이 분명 생깁니다.
중간 중간 latent가 없을 수도 있고 모든 이전 순서를 반영할 수 없는 상황일 수도 있습니다.
이것을 해결하기위해 Non-sequential Autogressive modeling을 진행합니다.
이것을 어떻게 진행하냐면 관측된 random variable을 조건으로 distribution을 만드는 것입니다. 그렇게 random으로 얻어진 data 속에서 순서대로 autogressive하게 modeling한다면 이전의 단점을 줄일 수 있습니다. 그런데 random하게 순서를 정하면 망하지 않나..? 라는 생각을 했는데 transformer를 활용하여 이러한 random set에서도 latent vector를 뽑아낼 수 있다고 합니다. 이렇게 얻어진 latent vector를 decoder에 넣어서 map을 형성합니다.
Conditional Generation
Shape Completion
Shape completion을 수식화하면 다음과 같습니다.
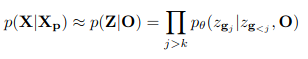
이것을 이용하면 shape completion을 할 수 있다고 합니다.
Approximating generic conditional distributions
shape completion은 조건부 확률 추론 문제로 해결할 수 있지만 다른 generation task에는 적용이 가능하지 않습니다.
우리는 P(X|C)를 바로 알고싶지만 이것은 쉽지 않기 때문에 latent space로 approximation을 할 것입니다. P(Z|C) = ∏p(zi|z<i,C) 하지만 data set이 부족하기 때문에 이러한 complex joint distribution은 사용 불가합니다. why? 계속 z<i와 C를 같이 고려하면서 학습을 하기 때문에 이것은 많은 양의 데이터를 필요로 하는 것입니다.
그래서 이 분포를 두 분포의 곱으로 나타냅니다.
pθ(zgj∣zg<j)와 pϕ(zgj∣C) 의 곱으로 나타냅니다.
pθ(zgj∣zg<j): 형상 사전 분포로 각 latent들이 영향을 주고 받는 것을 나타내는 분포입니다.
pϕ(zgj∣C): 조건 C가 각 latent들에 어떤 영향을 주는지 나타내는 분포입니다.
각 latent들은 독립이라 가정하기 때문에 이 두 분포의 곱으로 approximation할 수 있다고 합니다.
Learning Naive Condtionals
조건부 분포는 얇은 의자라는 텍스트가 주어지면 모델은 의자 다리 주변에 얇은 구조가 있을 것으로 기대합니다.
pi는 (X,C) data 쌍이 주어지면 loglikelihood pφ(z_i | C)를 최대화 할 수 있도록 parameter를 학습합니다.
Encoder로는 이미지의 경우 ResNet을 사용하고 언어는 BERT를 사용합니다.
Decoder는 업컨볼루션 디코더를 사용합니다.
Conclusion
그냥 학습할 때 prior information C를 넣어준다고 생각하면 좋겠네요
C는 두가지 정보를 넣어줄 수 있는데 언어와 이미지 정보입니다.
언어 정보는 BERT를 이용하여 잠재 벡터로 변해서 학습에 사용되고
이미지는 ResNET을 이용하여 잠재 벡터로 변해 학습에 사용됩니다.
그 이외는 독립을 이용하여 분포의 곱으로 approximation 했다는 내용이 중요한 것 같네요.
prior 정보를 어떻게 넣어주나 해서 봤는데 그냥 잠재벡터로 넣어주네요. 이런거 그냥 다 잠재벡터로 넣어줘야하나봐요. 그럼 20000
