1. Introduction
point cloud의 geometric processing은 더 중요해지고 있습니다.
sharp feature의 보존은 많은 계산과 modeling 적용을 위해 가장 중요한 고려사항입니다.
Feature는 discrete survace data의 normal vector를 계산하여 찾아집니다.
이 논문에서는 edge feature를 align할 curve를 정의하는 알고리즘을 제안합니다.
Robust Moving Least Squares 평면 기법에 기반하여, 처음에는 잠재적 feature point의 수를 선택합니다. RMLS 방식은 smooth feature를 못 뽑기 때문에 curve에 feature point를 projection하여 smooth하게 만들어 줍니다. 이 논문의 접근법의 장점은 input data가 조금 정렬이 잘 안되어 있어도 사용할 수 있고 속성 정보를 가정하지 않는 다는 것입니다.
Output feature curve는 smooth하고 complete하면 surface patch를 추출할 수 있도록 해줍니다.
2. Feature Extraction Algorithm
2.1 Preliminaries
이 논문의 방식은 unorganized set에서 작동합니다.
point P를 projection operator를 통해 surface에 projection 시켜 surface S를 정의합니다. 이 projection operator는 다양하게 정의할 수 있습니다. 보통은 근처의 point 들과 만드는 surface를 approximation을 통해 구하고 그 곳으로 projection 시킵니다.
이 방식은 moving least square(MLS)라고 합니다.
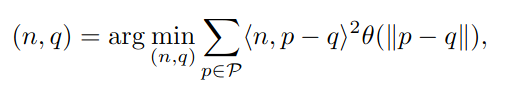
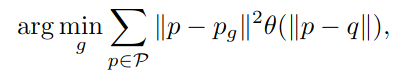
이 두식을 최적화를 하여 적절한 plane을 만들어냅니다.
이렇게 생성된 plane은 noise와 outlier를 수정할 수 있지만 동시에 sharp feature도 제거해버립니다.
이것을 보완하는 RMLS방식은 반복적으로 구해진 이웃점들을 활용합니다.
iteration 방식을 활용하고 forward search algorithm을 병렬적으로 사용하며 projection하기 적절한 plane을 찾아줍니다. 이 접근법은 noise를 찾고 sharp feature를 정의할 수 있다는 장점이 있습니다. 하지만 모든 point에 대해 계산을 진행하기 때문에 기존 MLS방식보다 조금 느립니다. 결국 이런 방식으로 surface를 정의하고 projection시키면 한가지 문제가 발생합니다. 모서리에 있는 점의 경우 두가지 surface에 모두 포함이 되는데 이는 잘못된 surface align을 만들 수가 있다는 점입니다. 이러한 문제를 해결하기 위해서 이 논문은 smoothing 과정을 도입합니다.
이를 통해 smooth하고 complete한 curve를 만들어 비교적 정확한 approximation을 진행합니다. 알고리즘의 과정은 다음과 같습니다.
(1) feature point 후보군들로부터 point cloud를 추출합니다.
(2) RMLS를 통해 surface를 만들고 point들을 projection시킵니다.
(3) covariance analysis를 통해 projection된 point들을 smoothing 해줍니다.
(4) smooting된 point들을 approximate한 polyline을 키워 feature line의 초기값을 생성합니다.
(5) 모서리를 연결하기 위해 끝 점들을 분석합니다.
결국 surface위주로 feature를 찾아내겠다는 것 같습니다.
2.2 Identifying Potential Edge Region
(1)에서 feature point 후보군을 뽑는다고 했는데 어떻게 뽑는지 알아보겠습니다.
MLS를 통해 surface를 만들게 되면 거기에 projection된 point와 point의 거리의 차를 구합니다.
이게 크면 클수록 edge에 있을 확률이 크기 때문에 이것이 일정 이상되면 edge region의 후보군으로 뽑는 것입니다.
2.3 Projecting Points to Edges
RMLS를 통해서 point들을 만들어진 feature에 projection 시킵니다. point가 할당되는 surface개수가 몇 개인지를 보고 그것이 이 feature의 종류를 말해줍니다.
하나의 surface만 할당된다면 이 point는 feature가 아니며 outlier일 뿐입니다.(Potential Edge로 뽑혔기 때문에) 2개라면 edge feature 3개라면 corner feature입니다.
2.4 Smoothing the Feature Points
Projection 과정의 output은 point set으로 나옵니다. 이러한 point들은 noise에 영향을 받아서 sharp feature를 뽑기에는 아직 적합하지 않습니다. covariance analysis를 통해 smoothing 하는 것에 영감을 받아 그 과정으로 feature point를 smoothing 해줍니다.
간단하게 설명하자면 주변 point와의 covariance를 계산 후 PCA하여 얻은 eigen vector로 평면을 정의합니다. 그 평면의 point를 projection하고 그 projection point에 대해 cross-corealation coefficient를 계산하고 그것이 일정 이상 크다면 eigen vector로 정의된 line에 잘 projection 됐다고 생각합니다. 이렇게 smoothing 과정을 통해 outlier를 제거하고 sharp feature를 얻을 수 있게 됩니다.
2.5 Feature Polyline Propagation
지금까지 뽑은 feature들은 정렬이 잘 되어있지 않습니다.
하지만 실제로 활용하기 위해선 연속적인 feature curve가 필요합니다. 이 파트의 목적은 feature point들을 polyline으로 잘 approximate하는 것입니다.
먼저 하나의 seed point를 중심으로 PCA를 진행하여 하나의 직선을 긋고 그 직선위에 projection된 point 중 가장 먼 두개의 점을 고릅니다. 이 두개의 점은 다시 seed point가 되어 이 과정을 반복합니다. 이것을 진행하면서 queue의 가장 첫 element를 제거하면서 중복을 막아줍니다.
2.6 Completing Feature Curve
end point의 tangent vecotr를 계산합니다.
feature point 주변 다른 feature point를 찾습니다. 3가지 케이스를 검색하는데
1번 gap completion 2번 corner creation 3번 endpoint identification
1번. 작은 거리 차이의 endpoint가 있는 경우 두개의 point를 이어 gap을 없애줍니다.
2번. end point에서 그은 line이 다른 feature point line안에 있는 point와 매칭 되면 새로운 코너를 제작합니다.
3번. 그대로 선을 그었을 때 아무것도 없으면 endpoint로 지정합니다.
결론: 결국 surface를 정확하게 정의하고 그것을 smooth하게 하여 robust하게 feature를 뽑는 것입니다.
계산이 많아 SLAM에는 적합하지 않겠다고 생각했는데 이것은 더 알아봐야할 것 같습니다.
