작성자 : 오진석

Contents

1. Motifs and Structural Roles in Networks
2. Subgraphs, Motifs, and Graphlets
3. Graphlets: Node feature vectors
4. Finding Motifs and Grphlets
5. Structural Roles in Networks
6. Discovering Structural Roles in Networks

---

we are going to talk about two topics about Network motifs graphlets and then the discovery of structural roles in networks

이번 3번째 강의에서는 Network motifs와 graphlets, 그리고 networks에서의 구조적 역할(discovery of structural roles)에 대해서 다루게 됩니다. 전체적인 graphs와 networks 보다는 구성 요소인 subnetworks에 대해서 보다 배우게 됩니다.

1. Motifs and Structural Roles in Networks

subgraphs는 networks의 구조를 identify하게 하고 다른 유형의 network와 구별할 수 있게 특징화하며 주어진 node를 통해 network의 구조를 describe할 수 있게 해줍니다. 예를 들어, 레고 또한 작은 레고들의 모음으로 만들어진 하나의 레고 집합이며, 작은 레고들은 서로 구별될 수 있는 모양과 역할을 가지고 있습니다.

그러므로 이번 강의의 목표는 bigger network를 구성하는 small network인 subgraphs(=sub networks)에 대해서 배우며 이러한 these building blocks에 대해 이해하는 것입니다.

위는 bigger network를 작은 구조의 network로 분해한 것을 보여줍니다. 3개 노드의 non-isomorphoic한 graphs는 총 13개의 경우의 수를 가지게 됩니다.

they have a different number of edges and in in what they differ is what are the directions of these edges and how many edges there are

이 모든 graphs들은 모두 non-isomorphic인 distinct한 특징을 가지고 있습니다.

isomorphic는 graph가 같은 edges와 같은 방향을 가지고 있으므로 다른 방법으로 그려짐에도 본질적으로 같은 grpah임을 의미합니다.

즉 non-isomorphic graph는 edges에 대한 다른 방향을 가지고 있으므로 본질적으로 동일하지 않은, 다른 graph임을 의미합니다.

그렇다면 이렇게 bigger network를 구성하는 subgraphs들의 frequency와 occurrence에 따라 정해지는 significant(중요성)에 대한 metric에 대해 생각해볼 수 있습니다.

the significance value가 negative 혹은 positive 하다면 network 내에서 under-represented 되거나 over-represented 라고 해석할 수 있습니다.

그렇게 되면 우리는 주어진 network에서 가능한 graph에 대한 significance profile을 작성할 수 있습니다.

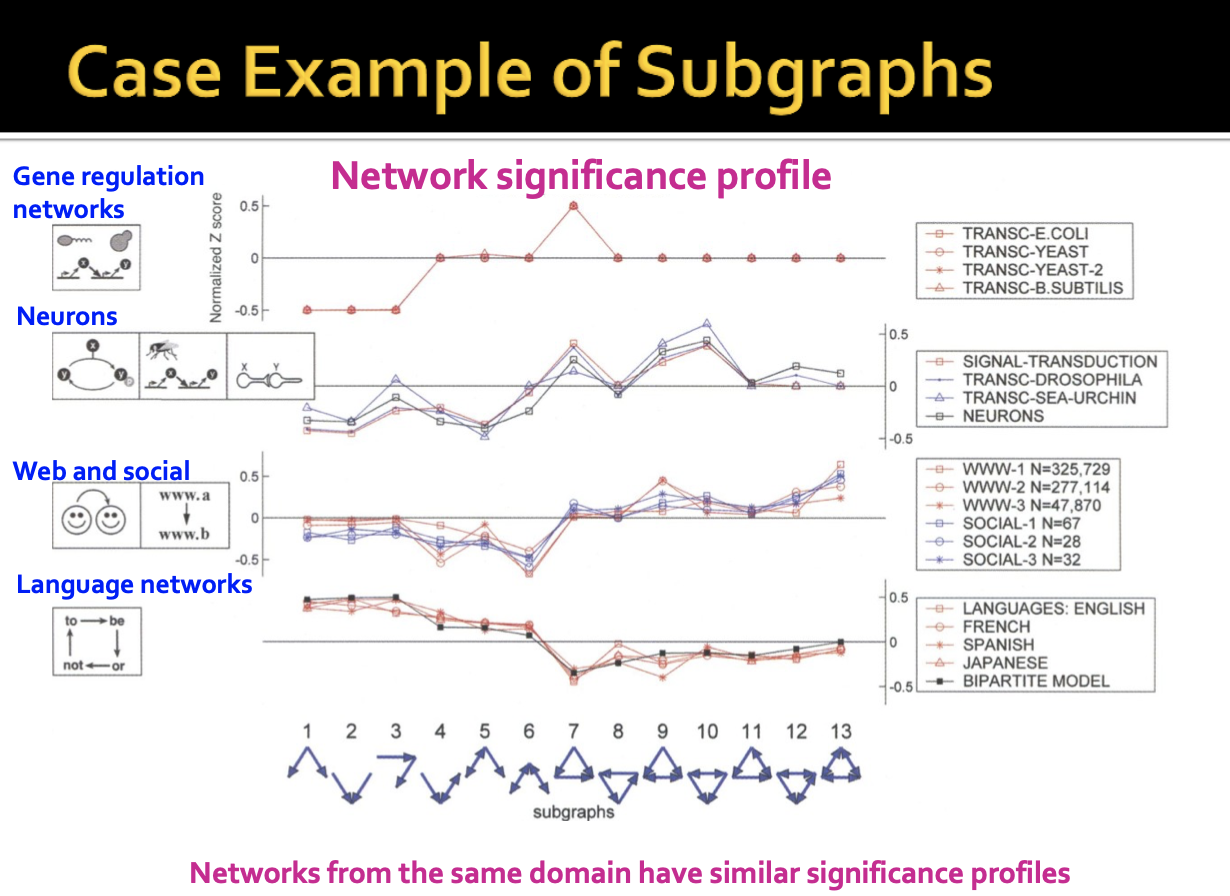
위는 다른 유형의 network를 보여줍니다. 앞서 언급한 3개의 노드에서 발생하는 유니크한 13개의 subgraphs가 있을 때, 다른 유형의 network에서 어떻게 significance가 달라지는지 확인해볼 수 있습니다.

각 network는 Gene regulation networks, Neurons networks, Web and social betworks, Language networks 입니다. 각 그림의 y축은 significance profile이며 network의 유형에 따라 subgraph의 significance가 달라짐을 볼 수 있습니다.

첫번째 subgraph의 significance는 Language networks에서는 over-represented이지만 Web and social networks에서는 under-represented 되었음을 알 수 있습니다.

그렇다면 어떻게 subgraph의 significance가 정의되고 계산되는지에 대해 학습할 수 있습니다.

이 강의에서는 3개의 주제에 대해 다루게 됩니다

• 먼저 subgraph에 대해서 다루게 되고 network motif와 graphlets의 개념에 대해 정의 후 motif와 graphlets을 찾는 알고리즘에 대해 배우게 됩니다.

• 이러한 개념에 기반하여, network에서 노드의 구조적 역활을 찾는 방법에 대해 배우게 됩니다.

• 마지막으로 활용 사례에 대해 다루게 됩니다.

• first we kind of we will talk about sub graphs and we will define a notion of network motif and we will define a notion of graphlets and then I will talk about algorithms to find motifs and graphlets

• using these types of concepts we will talk about how do we discover structural roles of nodes in the network

• I'll show you some applications of these things

2. Subgraphs, Motifs, and Graphlets

Network motifs의 정의는 significant recurring pattern of interconnections in the network 입니다. network motifs를 정의하기 위해서는 pattern, recurring, significant의 대한 개념을 정의해야 합니다.

• Pattern: Small induced subgraph, subgraph가 유도가 될 수 있는 패턴을 의미하는 것 같습니다.

induced: if you have a set of nodes then, you take all the edges between that set of nodes

• Recurring: it occurs muiltiple times with high frequency, 발생 빈도를 의미하는 것 같습니다.

• Significant: more frequent than expected, significant 혹은 more frequent라고 하기 위해서는 비교를 할 수 있는 baseline이 필요하다고 말합니다.

그렇다면 왜 sub structures, motifs가 필요할까요? 위에는 다른 유형의 motifs에 대한 예시가 있습니다. Motif는 어떻게 network가 작동하는지에 대해 이해할 수 있도록 해주며 주어진 상황에서 network의 operation과 reaction을 예측할 수 있도록 도와줍니다.

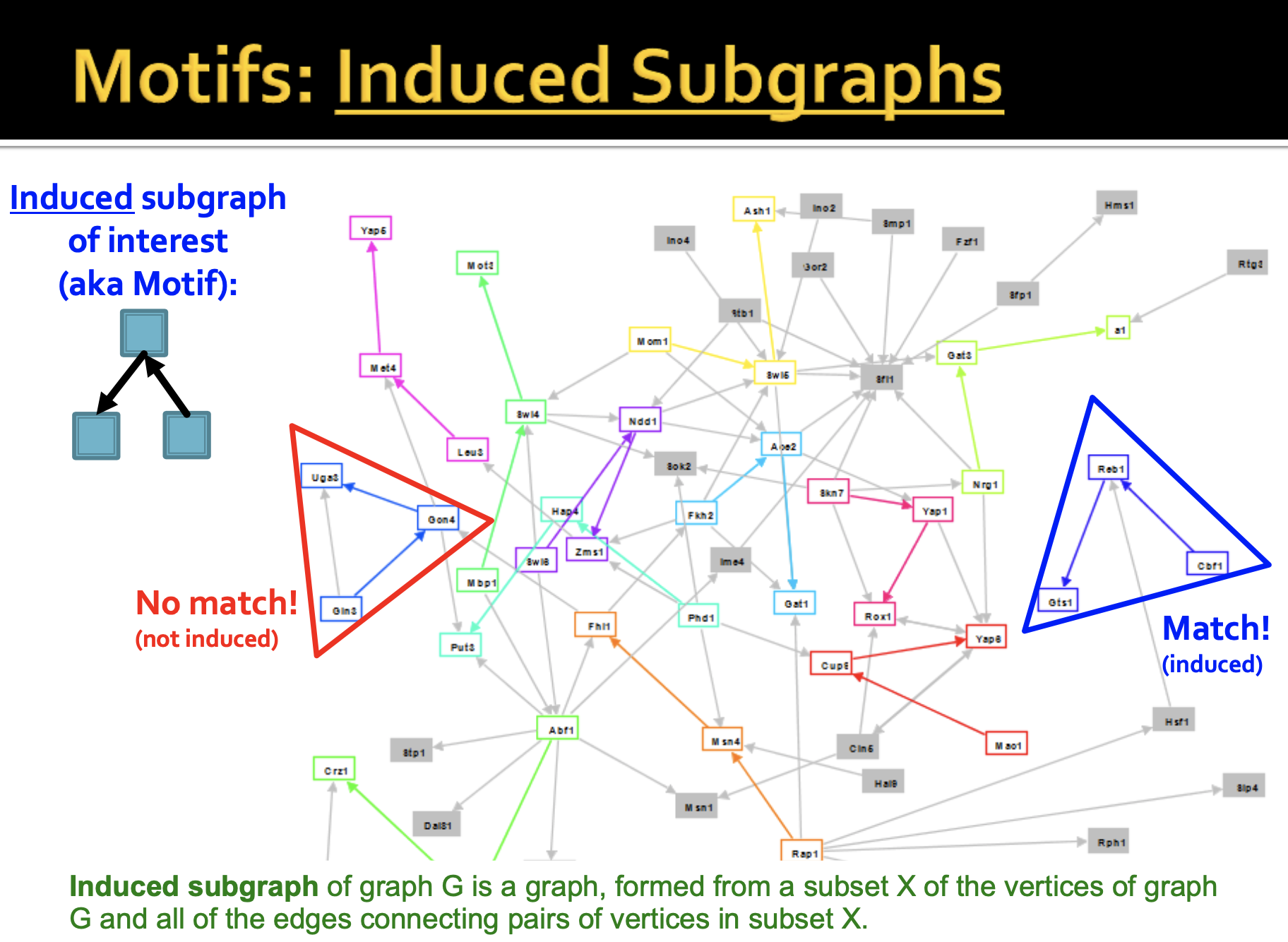
subgraph를 induced하는 과정에 대해 알아보겠습니다. motif of interest가 주어졌을 때, network에서 해당 subgraph가 나타나는지 찾아볼 수 있습니다. 주어진 motif는 3개의 node와 2개의 edges로 이루어져있는데, 빨간선의 subgraph에서는 3개의 edges로 이루어져있기 때문에 해당 motif라고 할 수 없으며 파란선의 subgrpah가 주어진 motif와 pattern이 동일하다고 할 수 있습니다.

즉, 빨간선의 subgraph는 내가 가지고 있는 pattern에 존재하지 않기 때문에 induced(유도)되지 못한다..라고 이해했습니다.

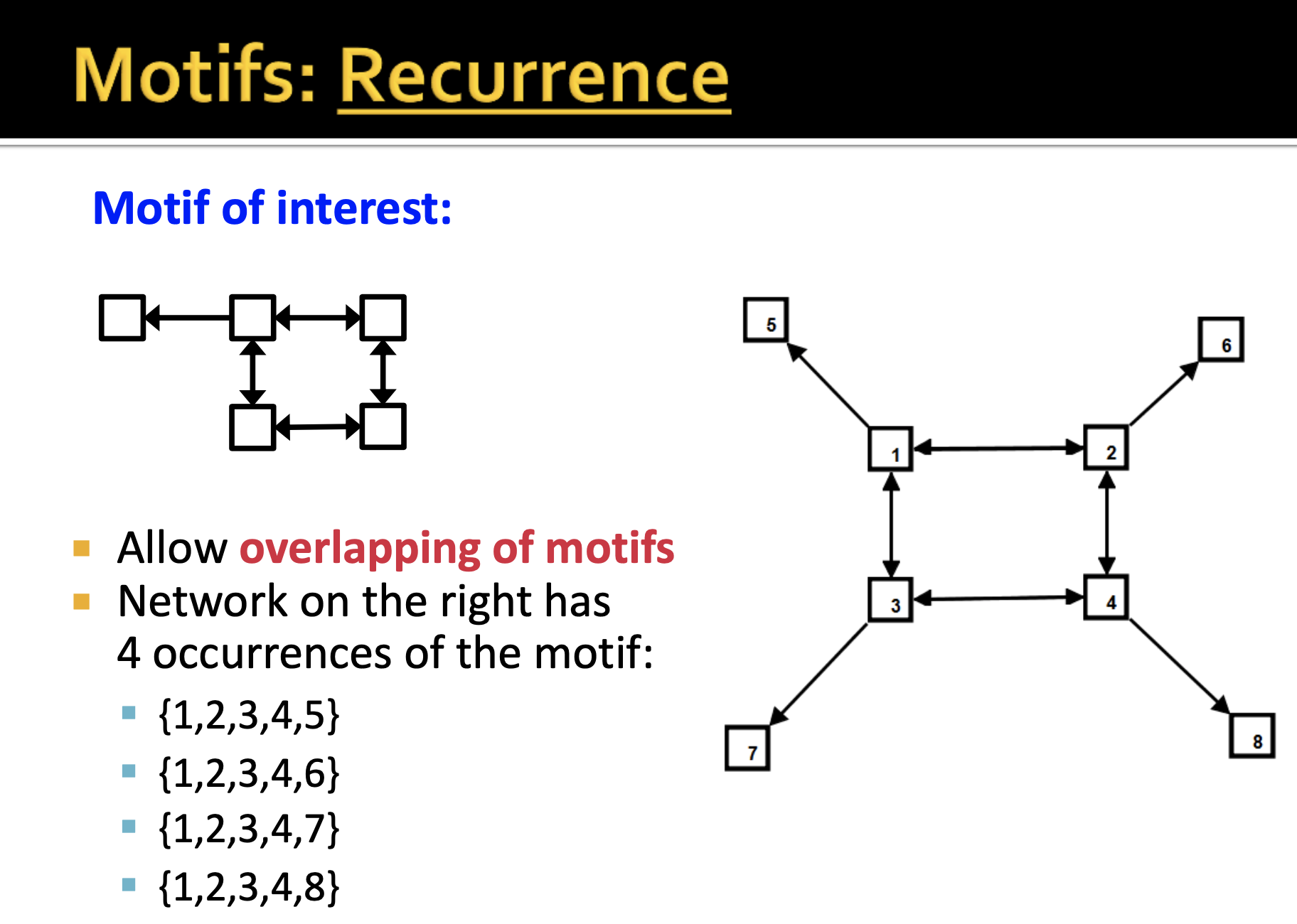
두번째는 recurrence의 개념을 정의하는 것입니다. recurrence의 개념은 중복을 허용하여 주어진 motif의 패턴이 몇 번 발견되는지 입니다. 위와 같이 어떠한 motif가 주어졌을 때, 다음과 같은 graph에서는 해당 motif가 4번 발견됩니다. node의 중복을 허용하기는 하지만 결과적으로 발견된 4개의 motif는 다르다고 할 수 있습니다.

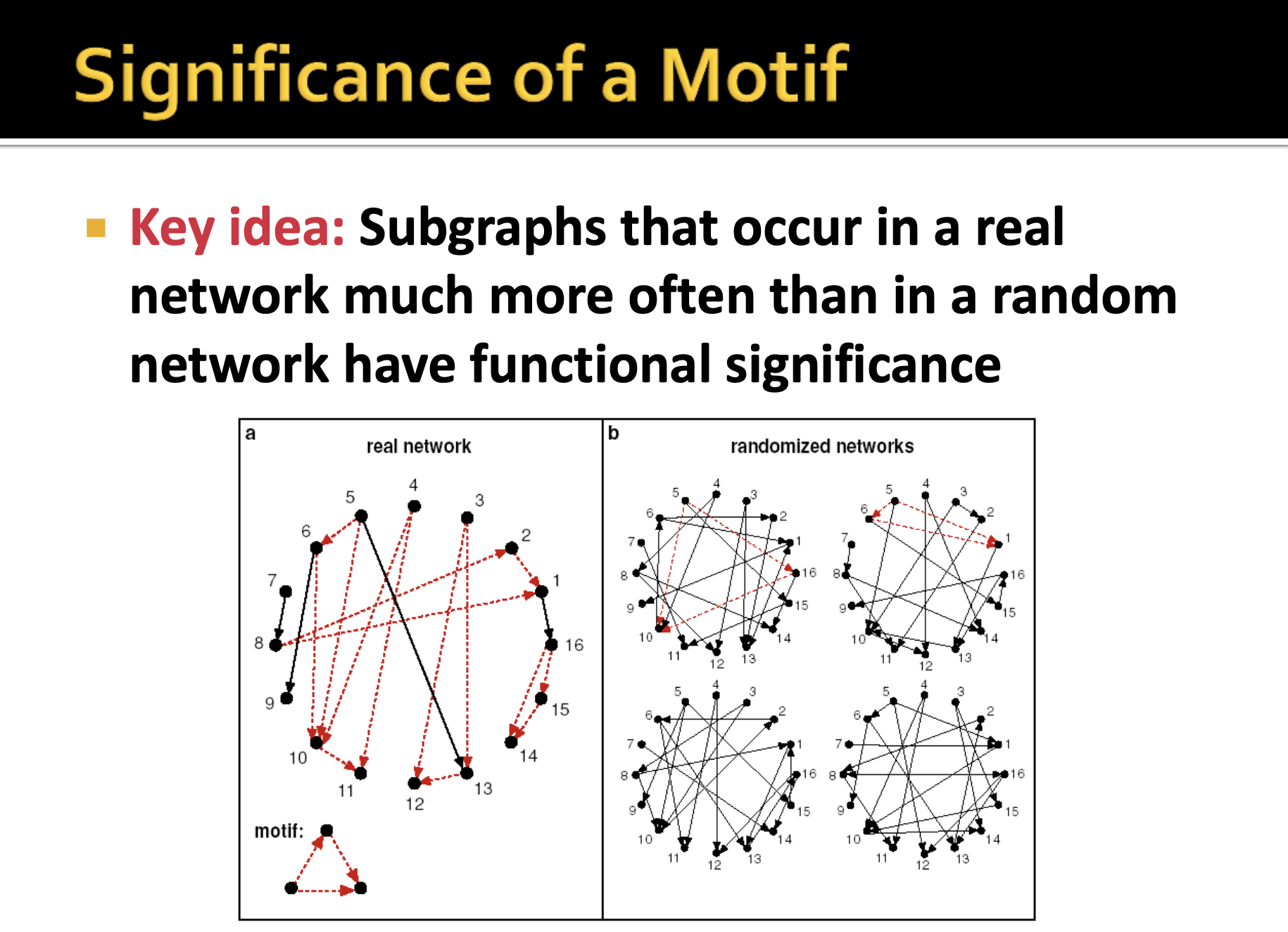
다음으로는 significance를 계산하는 과정을 가집니다. significance를 계산하는 핵심 아이디어는 비교하고자 하는 network와 랜덤 생성된 network에서 주어진 motif의 발생 빈도를 비교하는 것입니다.

그림을 보면 좌측의 target network에서는 주어진 motif(feed-forward loop)가 많이 발견되었고 우측의 랜덤하게 생성된 network에서는 거의 발견되지 않습니다. 이렇게 랜덤 생성된 network와 비교했을 때, 해당 motif는 target network에서 over-represented 혹은 over-expressed 되었다고 할 수 있습니다.

significance는 본질적으로 그저 z-score의 개념을 의미합니다. 랜덤 생성된 network에서 발견된 motif의 발생 빈도의 평균과 표준편차를 사용하게 됩니다. 여기서 랜덤 생성된 network를 일반적인 모집단과 같이 생각하는 것으로 이해했습니다.

다음으로 network significance profile를 정의하는 방법이 있습니다. z-score를 z-score의 제곱근의 합으로 나눠줌으로써 해당 motif의 SP, Significance Profile을 구할 수 있습니다.

SP를 계산할 수 잇는 방법에 대해서 학습하게 되었습니다. 그러나 아직 랜덤 그래프를 생성하는 방법에 대해서는 모르며 랜덤 그래프를 생성할 어떠한 null model이 좋은지에 대해서도 생각해보아야 합니다. 만약 null model을 가지고 있다면, 우리는 다수의 랜덤 그래프를 생성할 수 있고 significance 계산을 위한 모집단의 평균과 표준편차를 구할 수 있습니다. 그러므로 다음에 다룰 내용은 어떻게 랜덤 그래프를 생성하는지에 대한 방법입니다.

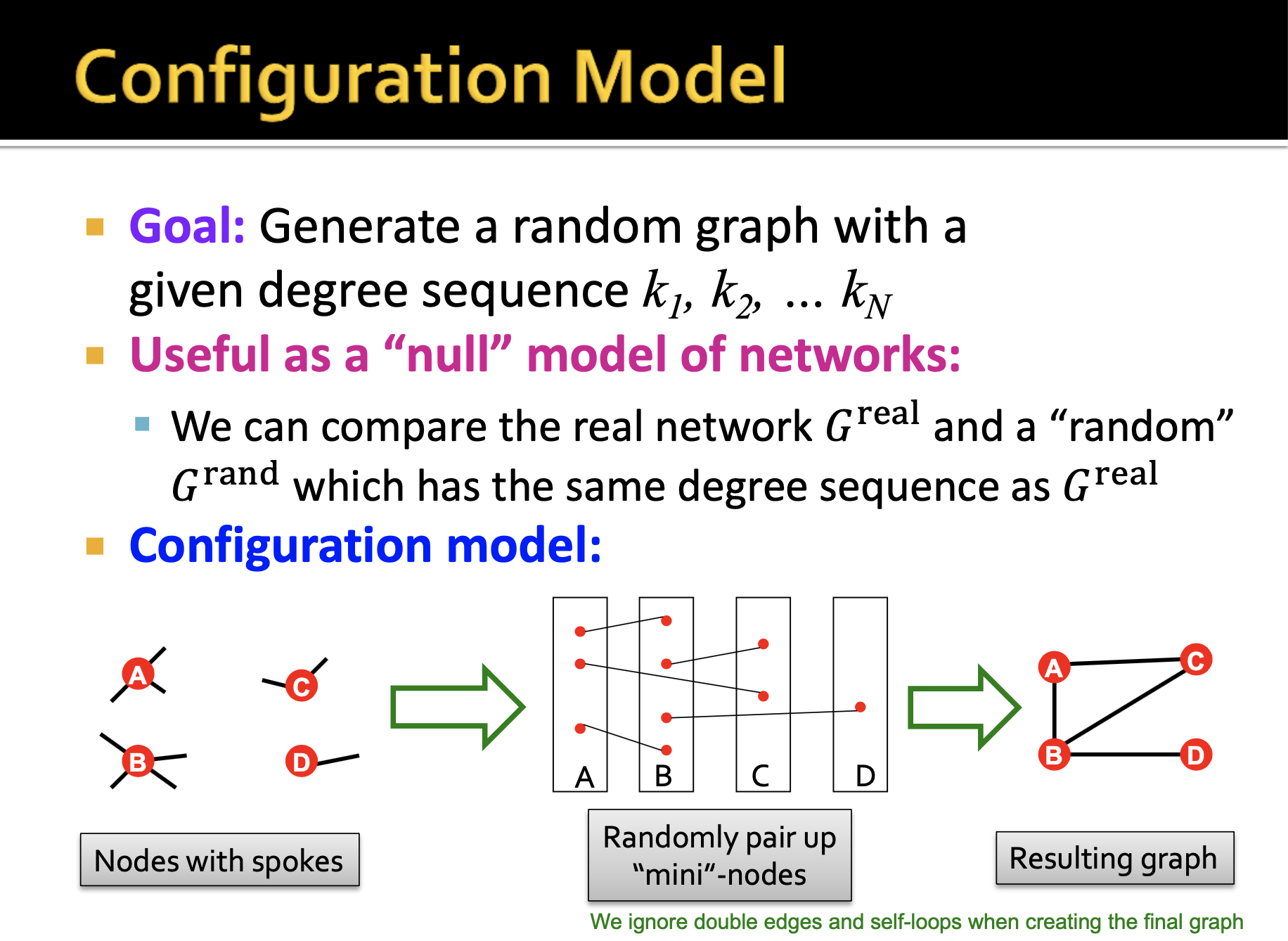
우리는 랜덤 그래프를 생성하고자 합니다. 주어진 degree sequence를 사용하여 랜덤 그래프를 생성할 수 있는데, 이 degree sequence는 real graph(target?)에서 온다고 합니다.

• Spoke

nodes가 존재할 때, 각 node는 주어진 degree를 가지고 있습니다. 이 degree는 spokes라는 half edges 개수를 의미하는 것으로 이해했습니다. half edges가 존재하는 nodes를 연결함으로써 랜덤 그래프를 생성할 수 있습니다.

노드를 하나의 파티션으로 생각하게 되었을 때, 각 파티션끼리 한번 이상의 연결이 존재하게 되면 두 노드 간 edge를 형성하고 우측과 같은 랜덤 그래프가 생성될 수 있습니다.

이러한 방법은 랜덤 그래프를 생성하는 굉장히 빠르고 효율적인 방법입니다. 하지만 Spoke를 이용한 Configuration Model generation은 ‘Double Edges’나 ‘Self-loops’는 고려하지 못해 기존의 주어진 degree sequence를 유지하지 못한다는 단점이 있습니다.

• Switching

Switching은 보다 expensive한 방법이지만 주어진 degree sequence를 정확하게 유지할 수 있는 방법입니다. 아이디어는 랜덤 edge 쌍을 선택하여 cross하는 방법입니다. (A-B), (C-D)라는 edge 쌍을 선택하게 되었을 때, endpoint를 cross하게 되면 (A-D), (B-C)라는 새로운 쌍이 나타나게 됩니다.

이렇게 주어진 edge를 교체(swap)하는 느낌으로 랜덤 그래프를 생성하게 되면 주어진 degree sequence는 철저히 준수할 수 있게 됩니다. 그러나 해당 rewiring화는 과정은 spoke 방법에 비해 매우 느립니다.

일반적으로 랜덤 그래프를 생성할 때에는, 10,000개에서 100,000개 이상의 랜덤 그래프를 생성한다고 합니다. 보통 real graph의 크기에 따라 생성되는 그래프의 개수가 달라지긴 합니다.

랜덤 그래프를 생성한 이후에는 real(target) graph에 존재하는 subgraph의 significance를 모두 구할 수 있고 가장 높은 significance를 가지고 있는 subgraph를 해당 graph의 network motif라고 할 수 있습니다.

3. Graphlets: Node feature vectors

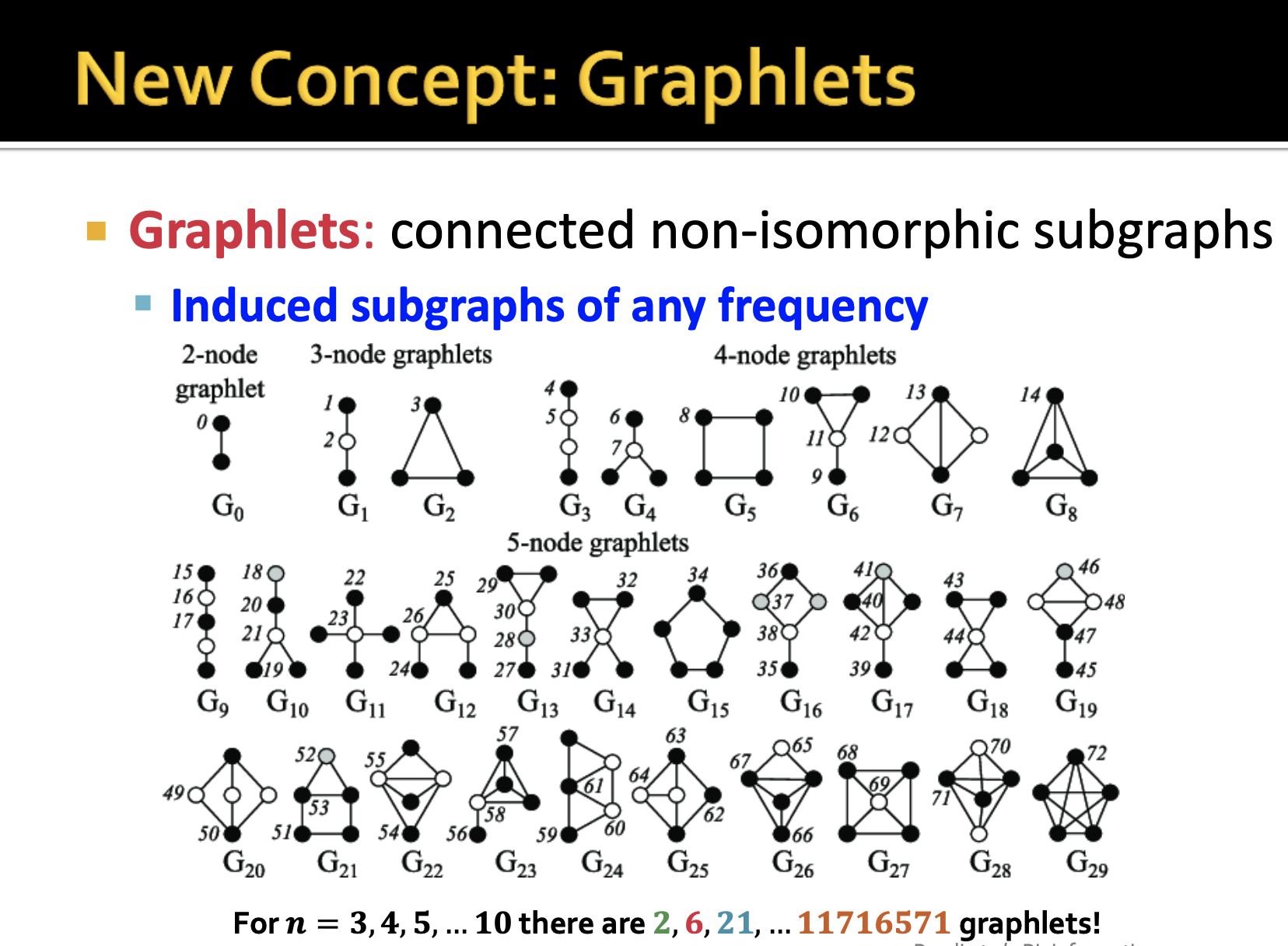
3번째 목차에서 배울 내용은 Graphlets라고 불리는 network motif의 extension입니다. graph motif의 개념을 사용하여 전체 network를 특징화할 수 있습니다. Graphlets의 개념을 사용한다면 주어진 node를 특징화할 수 있습니다. 주어진 node를 바탕으로 network 구조를 설명할 수 있게 됩니다.

전체 network에 대해서 다루기 전에, 네트워크 구성요소를 보고 node와 node 주변을 볼 수 있는데, graphlets에 의해 captured 된다고 합니다.

graphlets은 non-isomorphic한 subgraphs를 의미하며 위와 같은 subgraphs가 있습니다.

이러한 graphlets을 통해 node-level representation을 얻을 수 있습니다. motif가 전체 network에서 subgraph에 대한 metric이면, graphlets은 node에 대한 node-level subgraph metric이라고 할 수 있습니다.

여기서도 degree 개념이 차용되는데 노드의 인접한 edges의 개수라고 볼 수 있습니다. graphlet degree vector(GDV)는 주어진 노드가 연결된? 속한? graphlet의 개수

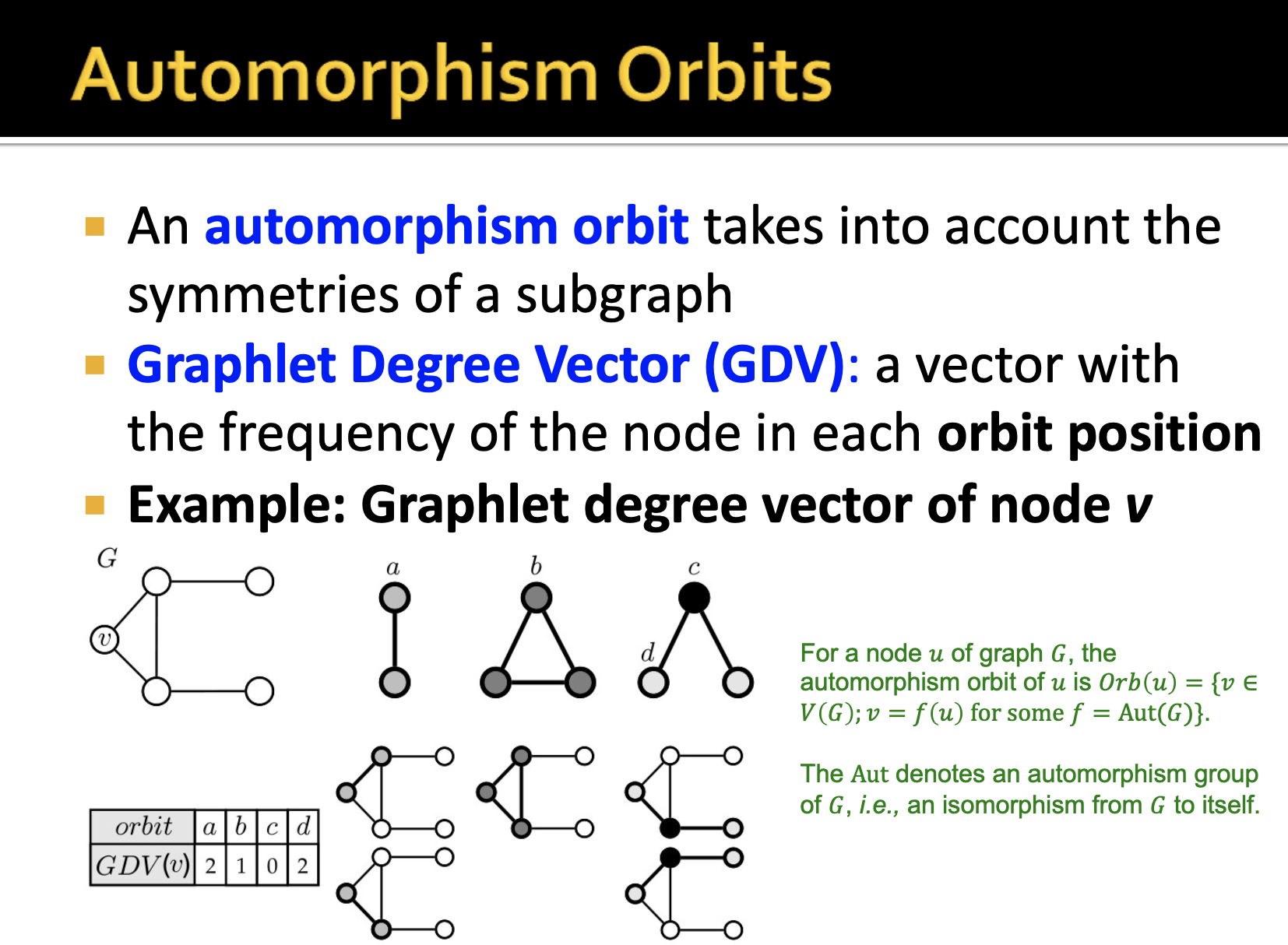
automorphism orbit은 주어진 subgraph에서 symmetries, 대칭성을 고려해줍니다. 여기서 graphlet degree vector(GDV)는 각 orbit position에서 node의 빈도에 대한 벡터를 의미합니다.

v 노드를 기준으로 GDV를 구하게 되면 c가 v 노드라고 가정했을 때 해당 graphlet이 존재할 수 없기 때문에 0번 발견됩니다.

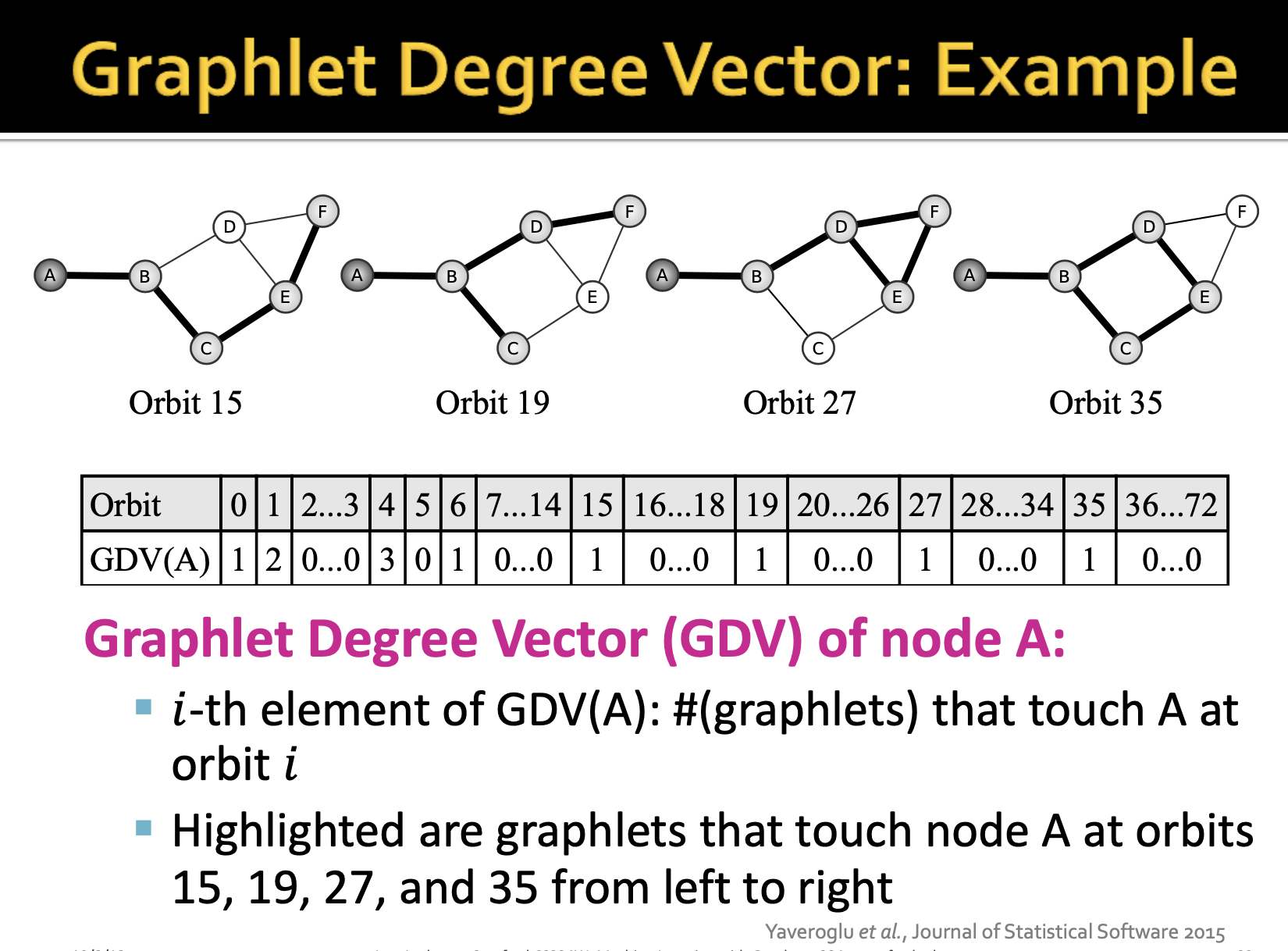
이런식으로 GDV는 하나의 노드를 기준으로 73개의 차원으로 구성된 벡터라고 할 수 있습니다. 그렇기 때문에 이 벡터를 가지고 노드를 특징화할 수 있으며 다양한 것에 활용해볼 수 있습니다.

4. Finding Motifs and Grphlets

그렇다면 어떻게 motifs와 graphlets를 발견할 수 있을까요. 그리고 수학적으로 어떻게 motifs와 graphlets을 계산하여 식별할 수 있을까요. motifs와 graphlets을 발견하기 위해서는 2가지 challenges를 해결해야 합니다.

K-size의 motifs와 graphlets을 찾는다고 가정한다면, 2가지 단계를 거치게 됩니다.

• Enumerating: K-size의 가능한 모든 subgraphs를 찾는 과정
• Counting: 찾은 모든 subgraphs의 occurrences를 세는 과정

하지만 이 과정에서 매우 복잡한 computational problem인 np-complete 문제가 발생하게 됩니다. 보통 motifs와 graphlets가 5개에서 8개의 노드로 구성되면서 combinatorial explosion이 발생되기 때문입니다.

이번 강의에서는 Enumerating과 Counting을 위한 방법으로 2006년에 제안된 ESU 알고리즘을 다루게 됩니다.

ESU 알고리즘은 v 노드를 시작으로 새로운 노드를 추가해나가면서 subgraph를 만들어나가는 과정을 거칩니다. ESU 알고리즘은 재귀적 구조를 가지고 있으며 현재 시점의 subgraph를 저장하는 $V_{subgraph}$와 motif를 확장하기 위한 후보 노드를 보관하고 잇는 $V_{extension}$로 구성되어 있습니다. $V_{extension}$의 후보 노드가 $V_{subgraph}$로 이동하게 되면서 state가 업데이트되는 과정에서 재귀 구조가 발생한다고 볼 수 있습니다.

ESU 알고리즘의 수도코드는 위와 같습니다.

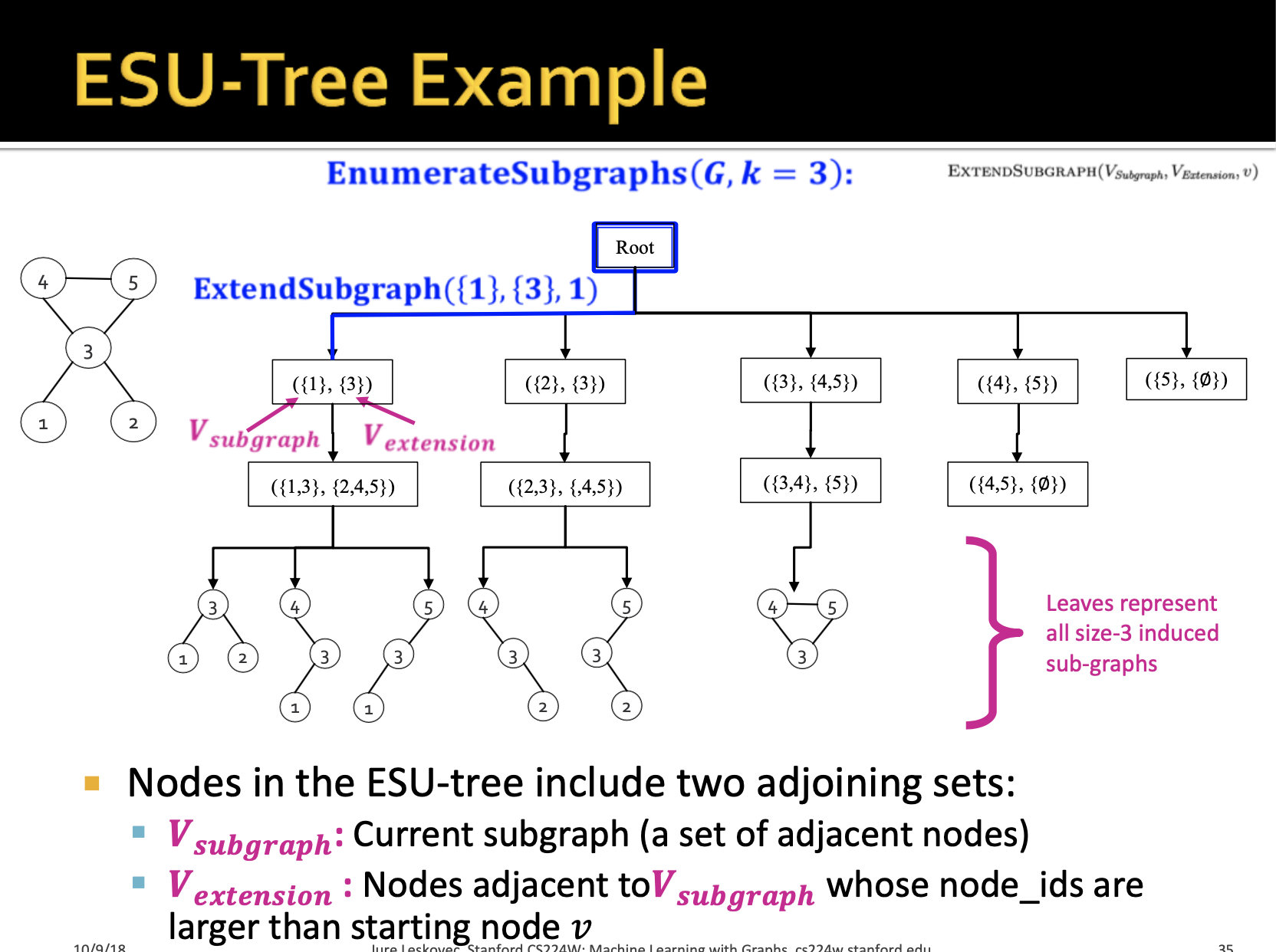
예시를 확인하게 되면 보다 쉽게 이해할 수 있습니다. 1번~5번의 노드로 구성되어 있는 그래프 G가 있을 때, k개의 depth(노드 개수)의 subgraphs를 추출할 수 있습니다. 먼저 각 노드를 시작점으로 생각하면 자연스럽게 확장 가능한 후보 노드를 $V_{extension}$에 저장할 수 있게 됩니다.

1번 노드를 시작으로 하게 된다면 1번 노드와 연결되어 있는 3번 노드가 $V_{extension}$에 추가될 것이고 아직 $V_{subgraph}$의 개수가 3이 되지 않았기 때문에 후보 노드 중 하나를 추가하는 재귀가 발생하고 $V_{subgraph} = {[1,3]}$이 되면서 3번 노드와 연결되어 있는 2,4,5번 노드가 $V_{extension}$에 추가됩니다. 그렇게 다시 한번 재귀 구조가 발생하면서 depth가 3인 subgraphs를 뽑아낼 수 있게 됩니다. 여기서 주의해야할 점은 후보 노드는 항상 시작 노드 v보다 크게 함으로써 중복을 피할 수 있게 됩니다.

이렇게 가능한 subgraph를 찾는 과정이 Enumerating 과정입니다.

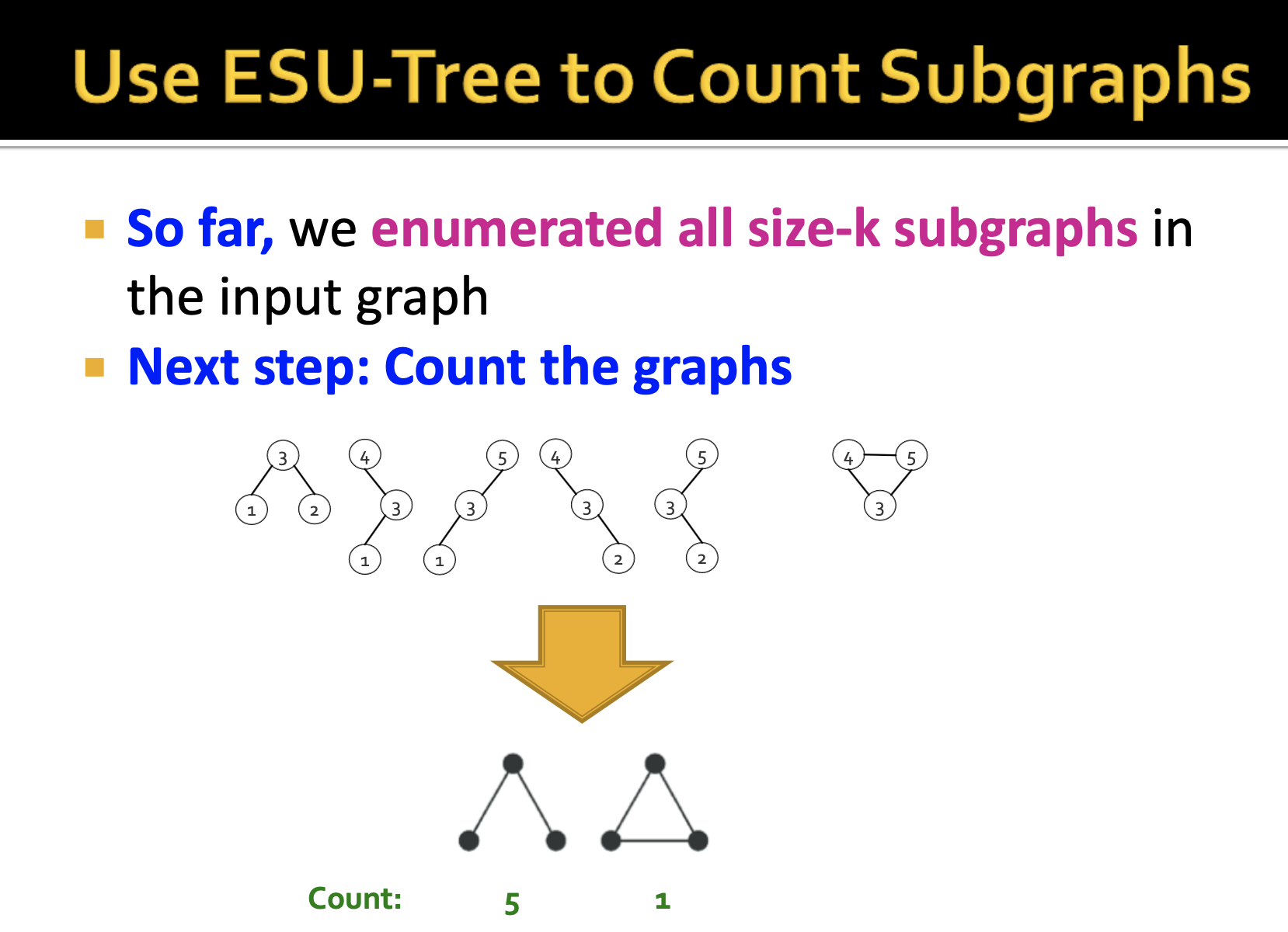
다음 단계는 Counting 과정입니다. count를 하는 기준은 non-isomorphic한 graph를 토대로 subgraphs의 개수를 세주는 것입니다. 즉, 3개의 노드와 2개의 edge로 구성되어 있는 subgraph는 topologically equivalent한 isomorphic한 graph이기 때문에 해당 구조가 총 5번 나왔다고 할 수 있으며, 이 때 isomorphic을 구별하기 위해 Mckay's nauty algorithm을 사용했다고 합니다.

5. Structural Roles in Networks

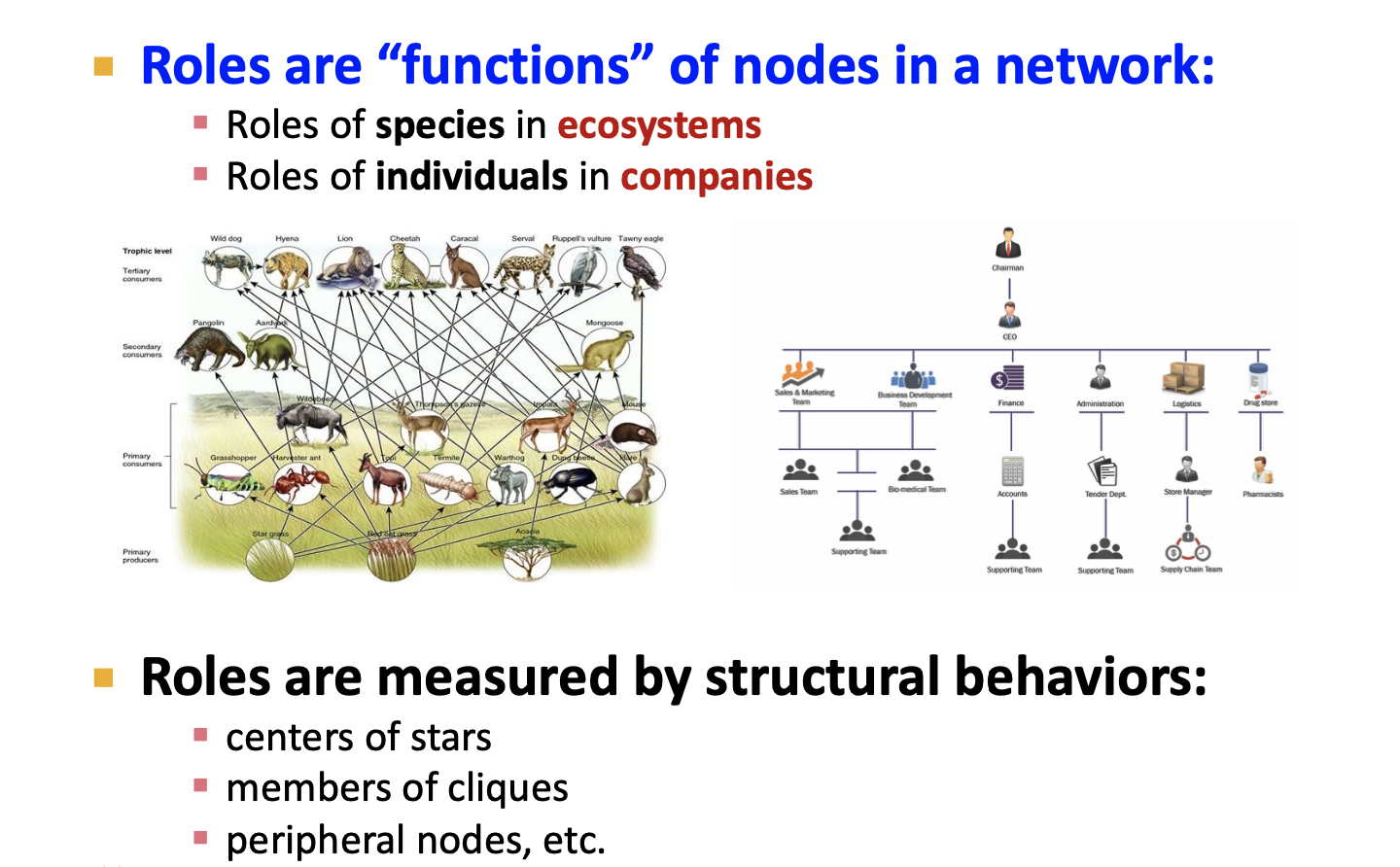
Roles 은 네트워크에서 노드의 function이라고 할 수 있습니다. 일반적으로 생태계에서 종의 roles, 그리고 회사에서 개인의 roles와 같은 개념이라고 볼 수 있습니다. 회사에서 직무에 따라 부여되고 책임을 지는 roles이 달라지는 것처럼, 궁극적인 목표는 네트워크 구조에서 노드의 Roles를 식별하는 것입니다.

Role은 네트워크에 존재하는 비슷한 위치 및 기능을 가지는 nodes의 집합을 의미하는 자료구조라고 할 수 있습니다. 여기서 강조하는 부분은 Role은 Group 혹은 Community와는 다른 개념이라고 말합니다. Role은 similar position이라는 특징을 가지지만 무조건 연결되어 있을 필요는 없다고 합니다. 하지만 Group/Community는 서로가 densely하게 연결되어 있어야 합니다.

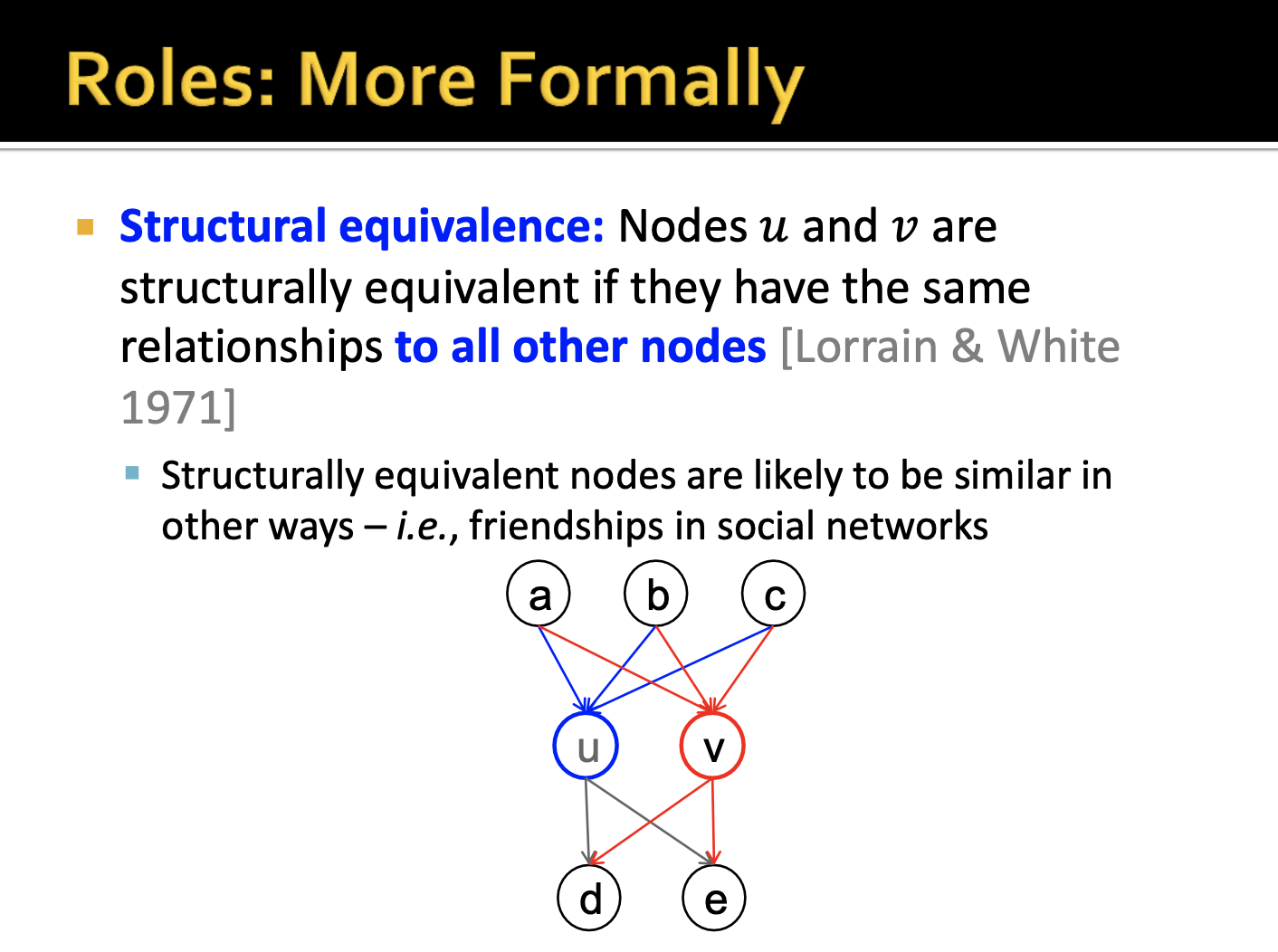
그렇다면 similar position 혹은 similar structural properties로 네트워크 내의 Role을 판단하기 위해서 Structural equivalence라는 개념이 사용됩니다. Structural equivalence는 노드 U, V가 다른 노드와의 관계가 동일하다면 구조적으로 동등한 role로 볼 수 있음을 의미합니다.

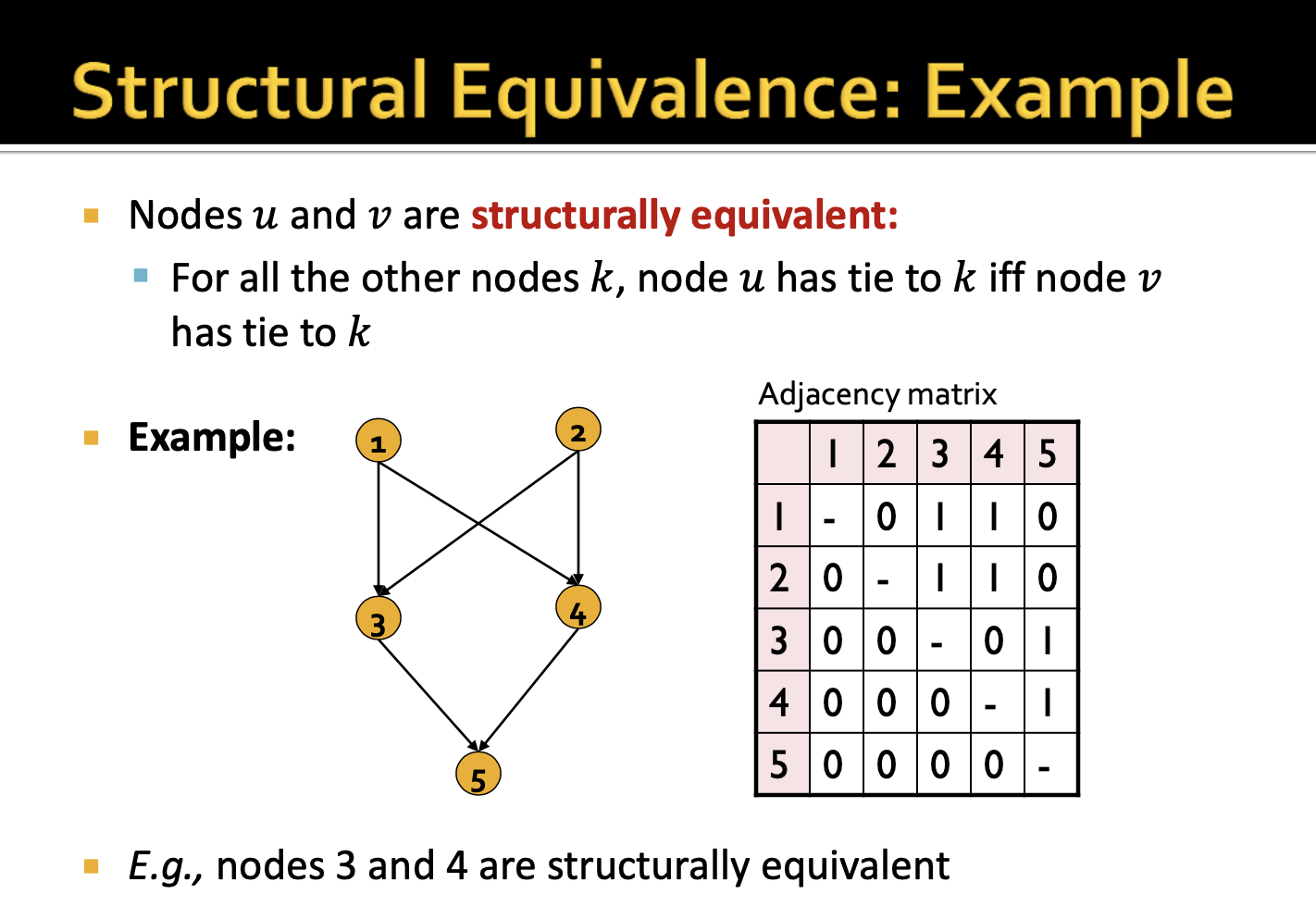
해당 예시 그래프에서 노드 3, 4가 Structural equivalence임을 알 수 있습니다. 노드 간 structural equivalence를 찾을 때에는 어느정도의 noise를 감안하기도 합니다.

6. Discovering Structural Roles in Networks

Roles은 네트워크 구조에 존재하는 노드의 서로 다른 특징을 구별해주기 때문에 매우 중요합니다. 또한 노드의 Roles를 가지고 위와 같은 여러 과제를 수행할 수 있습니다.

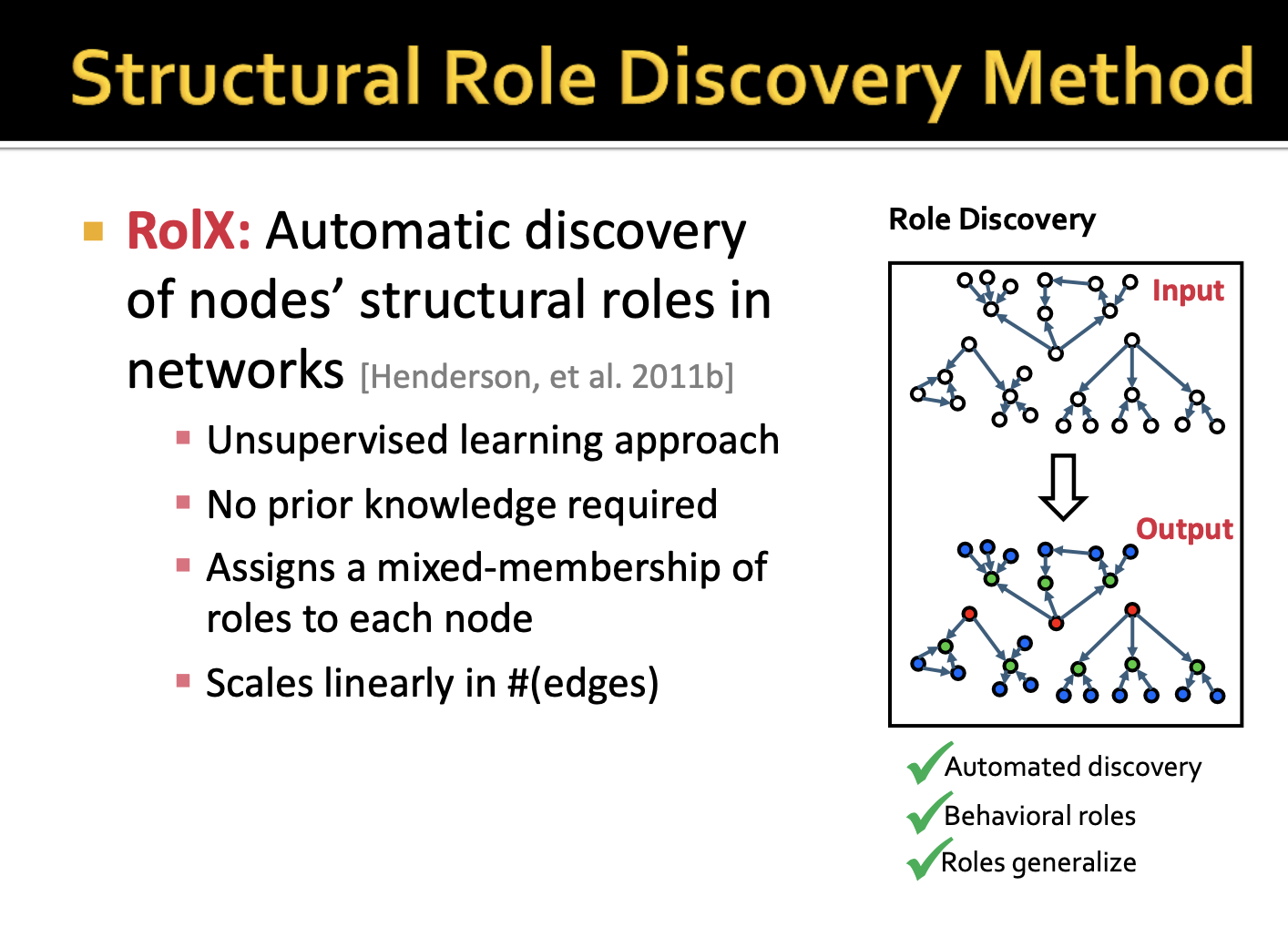
각 노드의 네트워크 구조 상 roles를 자동으로 찾아주는 방법으로 RolX가 있습니다. 해당 접근법은 unsupervised learning 방법에 속하며, 사전 정보를 요구하지 않습니다. 그리고 각 node에 mixture of roles를 부여하게 됩니다.

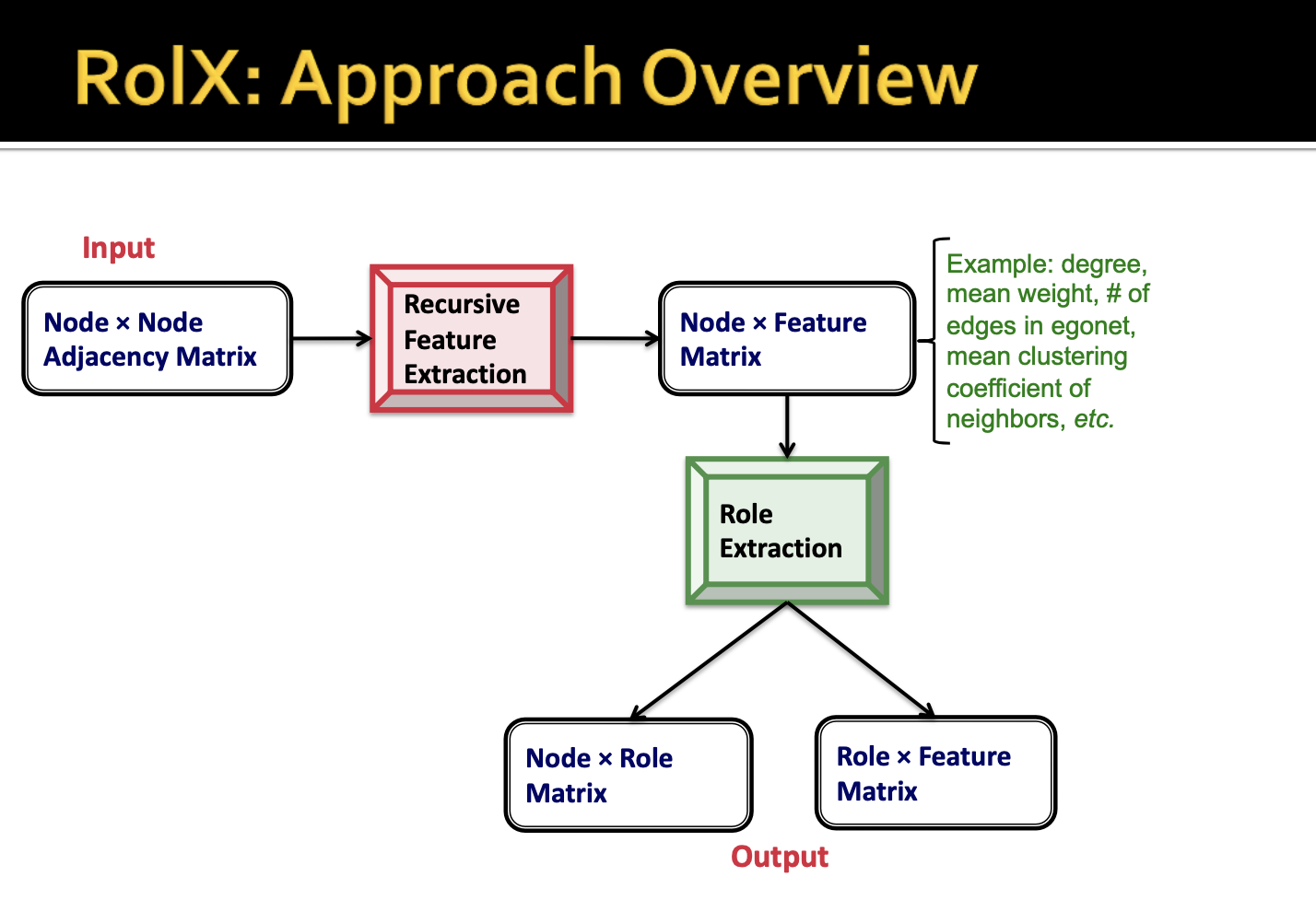
RolX에서 node의 role를 추출하는 과정은 다음과 같습니다.

• Node * Node 인접 행렬을 생성합니다.
• 모든 Node별 재귀 구조를 통해 descriptor를 생성해줍니다.
• 그 다음 Node * Feature(descriptor)이라는 새로운 행렬을 만들어줍니다.
• Role Extraction을 통해 Node별 Role에 대한 행렬과 Role을 설명해주는 Role * Feature 행렬이 output으로 나오게 됩니다.

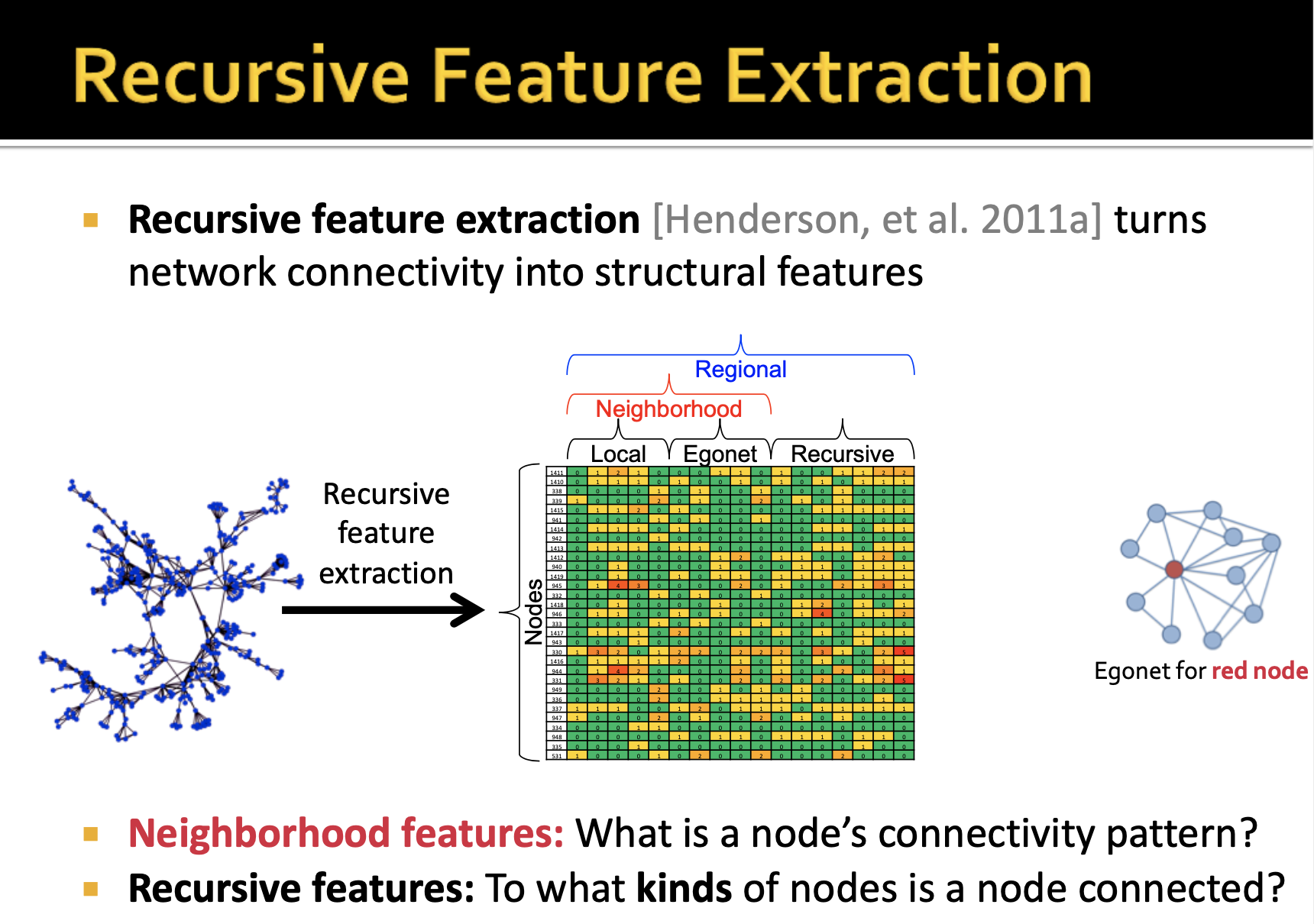
node에서 feature를 추출해내는 재귀 구조에 대해서 한번 알아보도록 하겠습니다. 어떠한 재귀 구조가 형성되는지 언급하지는 않았지만 개인적으로는 인접 행렬의 정보를 기반으로 feature를 추출할 것이라고 이해했습니다. 결과적으로 Node * Feature 행렬이 만들어 지는데, node와 local network에 대한 정보와 neighborhood 정보, 그리고 노드와의 연결성에 대한 recursive 정보까지 포함한다고 말합니다.

이러한 feature extraction의 핵심 아이디어는 노드의 정보를 모아 새로운 recursive features를 생성하는 것이라고 할 수 있습니다.

• Local Features: 노드의 차수에 대한 모든 측정치

  • 방향 그래프라면, include in- and out-degree, total degree
  • 가중 그래프라면, include weighted feature versions

• Egonet Features: 노드의 egonet에서 계산되는 값

  • Egonet은 노드에서 유도된 subgraph의 노드와 이웃 그리고 모든 edges를 포함합니다.

base set of features 가 형성되었으면 집계를 통해 features를 더욱 확장시킬 수 있습니다. mean과 sum 이라는 2개의 집계 함수를 사용해서 이웃 노드의 평균 차수 혹은 이웃 노드 차수의 합 등과 같은 feature를 계속해서 늘려나갈 수 있게 됩니다.

그런데 재귀를 돌 때마다, 계산해야할 features의 수가 급증하기 때문에 pruning technique이라는 기법을 통해 features의 수를 줄일 수 있다고 합니다.

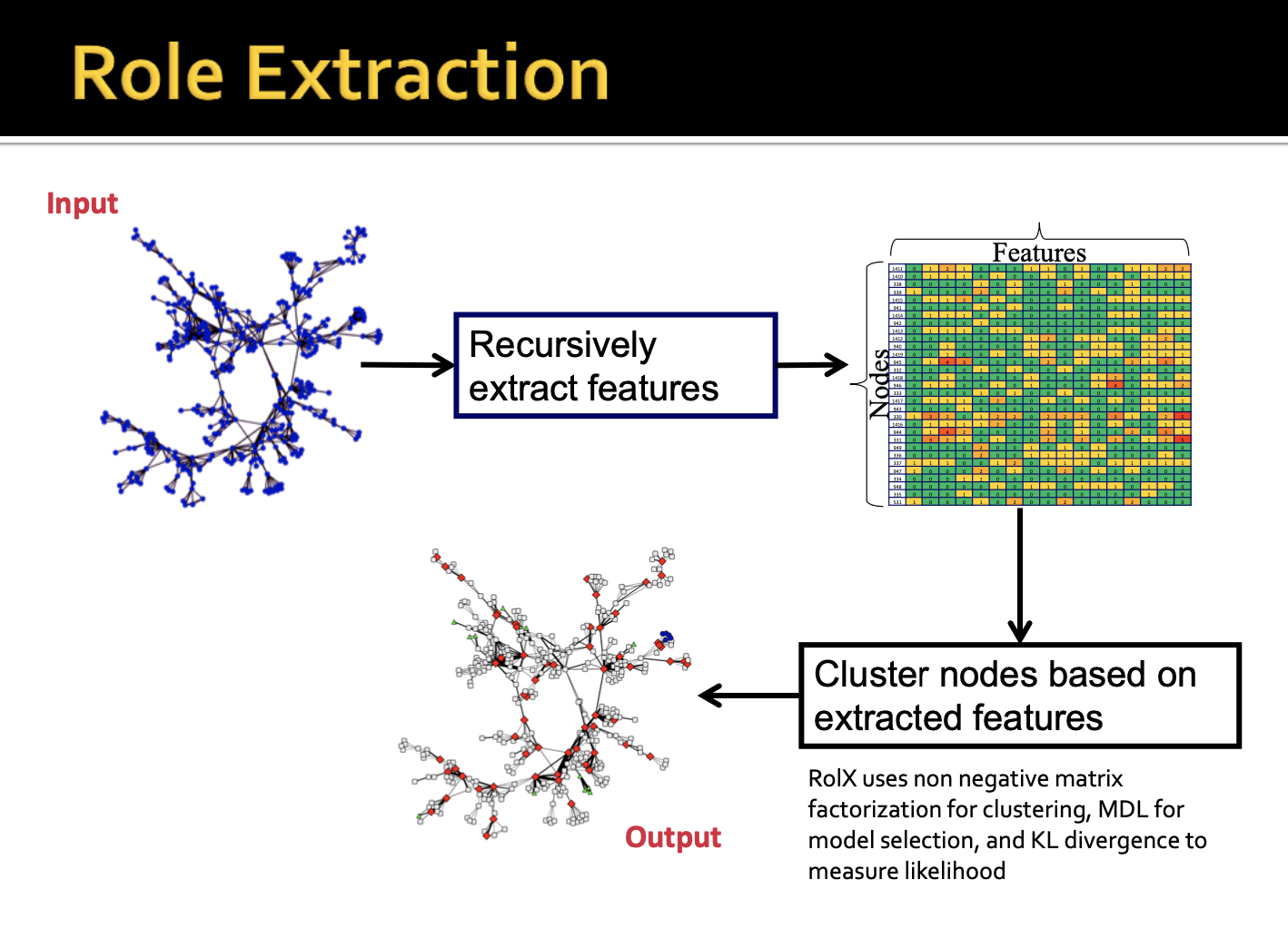
각 노드별로 노드를 표현할 수 있는 features가 벡터로 표현되었다면 clustering을 통해 Roles를 표현할 수 있게 됩니다. 이 때, 다양한 접근법의 clustering을 모두 적용해볼 수 있습니다. clustering 결과를 바탕으로 네트워크 상의 구조적 roles를 부여할 수 있고 role distributions을 통해 노드 간 유사도 또한 계산해볼 수 있습니다.

참고 자료

• Tobigs graph study, Chapter3. Motifs and Structural Roles in Networks
• 데이터 괴짜, CS224W - 03.Motifs and Structural Roles in Networks
• 이현준, cs224w 3강 정리( Motifs and Structural Roles in Networks)
• Wikidocs, 03-02 Finding motifs and graphlets