작성자: 투빅스 16기 김종우
Contents
1. Vanishing Gradient
2. LSTM
3. GUR
4. More fancy RNN variants
1.Vanishing Gradient
Vanishing Gradient problem for RNN
Gradient Problem
- Backpropagation 시 gradient가 너무 작거나, 클 때 학습이 제대로 되지 않는 경우
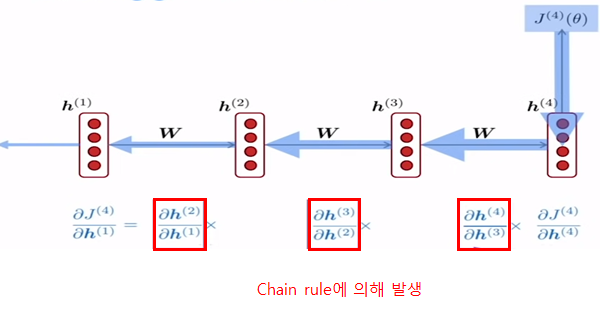
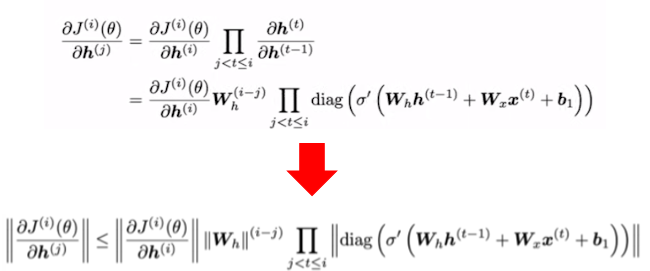
가중치 Wh는 l2 norm(크기라고 이해)은 가장 큰 고유값으로 결정이 되며, 이에 대한 증명은 아래의 사이트를 참조 하시면 됩니다.
wh이 1보다 작으면 gradient vanishing이 발생하게 되며, 1보다 클시 exploding이 발생하는 것으로 생각하시면 됩니다.
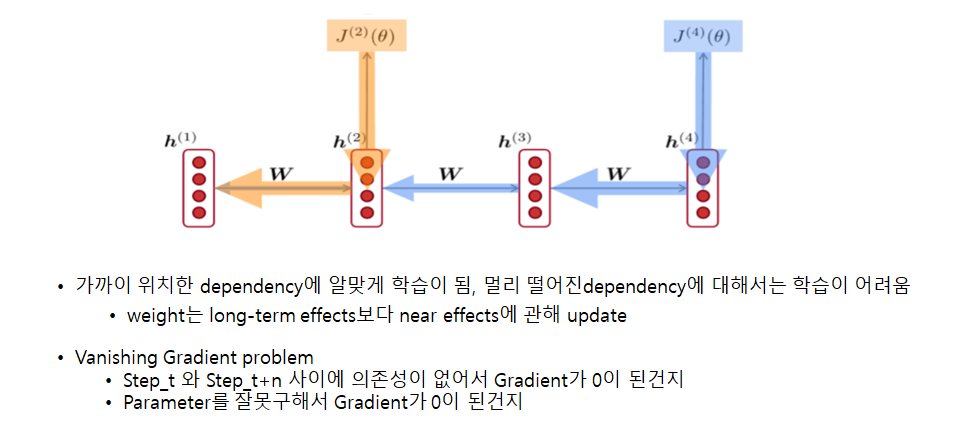
step 4 시점에서 gradient를 구하면 점점 갈수록 영향력이 줄어드는 것을 볼 수 있습니다. 하지만 step2 시점에서 gradient를 구하면 가장 가까운 곳은 영향력이 강한 것을 보실 수 있습니다
아래의 밑줄 친 부분은 tickets이 나와야 합니다. 하지만 gradient vanishing의 문제로 예측해야 할 곳과 거리가 먼 정보를 잘 전달받지 못하기 때문에 가장 최근에 나온 문장으로 본 밑줄을 예측해 printer라는 잘못된 정답이 나오게 됨.
원래 빈칸의 정답은 writer를 따라 is 가 되어야 합니다 하지만 멀리 위치한 단어에 대한 정보가 줄어들다 보니, 가장 가까운 books를 보고 are이라고 예측하는 경우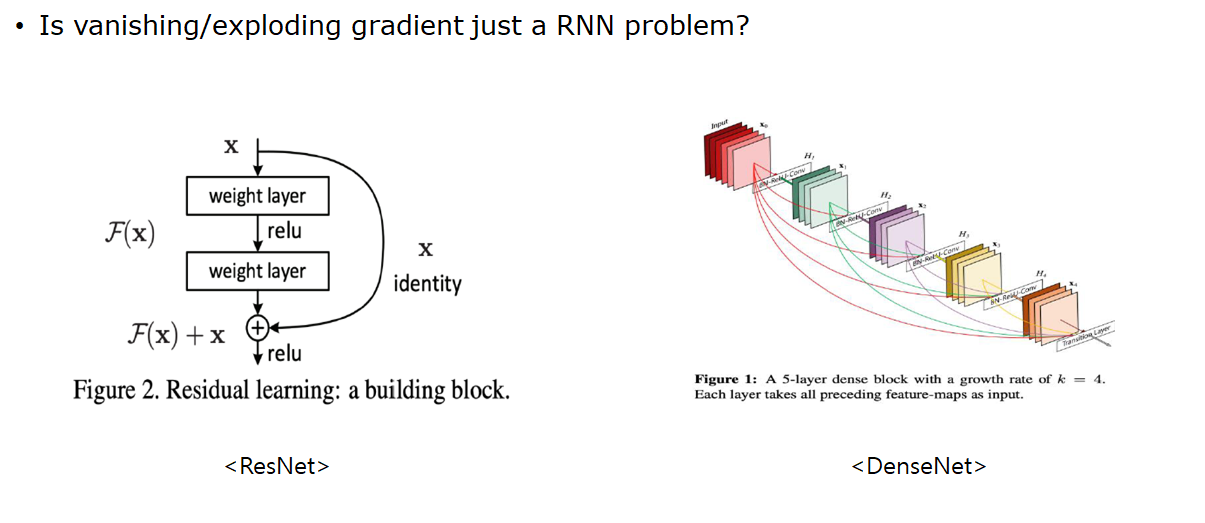
resnet은 input 정보 x를 마지막 계산에 더해주어 fx+x라는 식을 만들어주게 됩니다. 이때 gradient를 구하기 위해 x에 대한 편미분을 진행하면 fx+1이 되게 됩니다. 이때 편미분을 한 본래의 gradient fx가 아무리 작아도 x를 미분한 1이 남아있기 때문에 gradient vanshing이 발생하지 않음.
densenet은 element들을 더하는 resnet의 방식과 달리 layer를 지날수록 input값들을 output값에 concatenat를 해주게 되면서 크기를 점차 키워나감.
2.LSTM
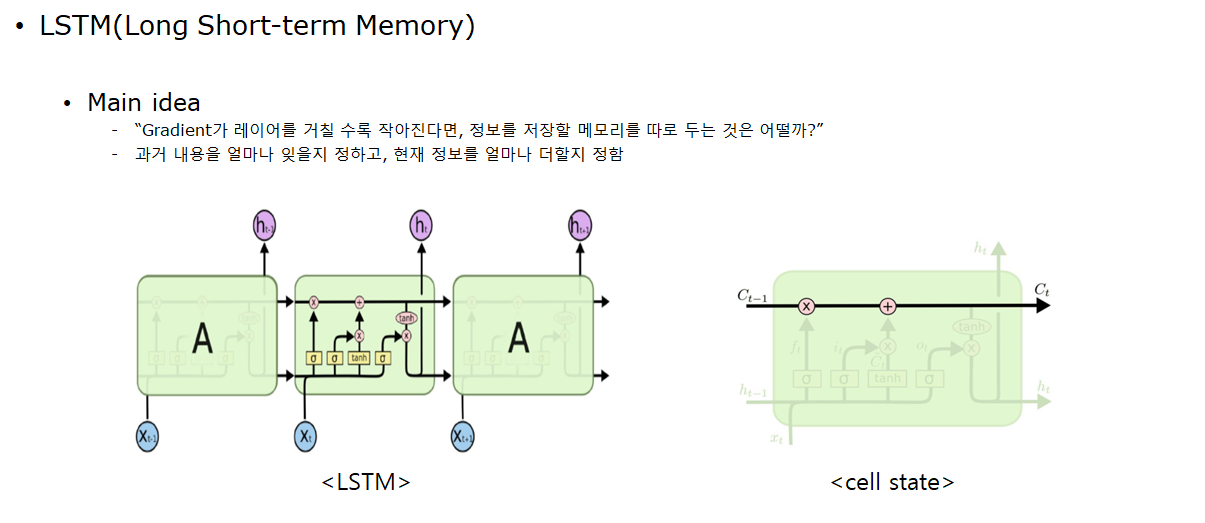
cell state가 과거 정보들을 계속 보존할 메모리 역할함.
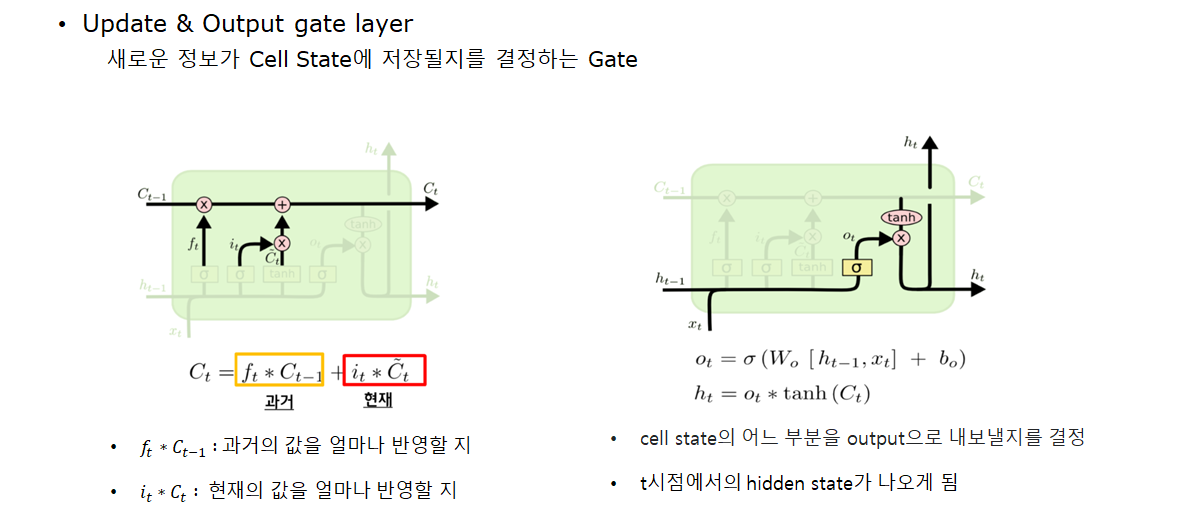
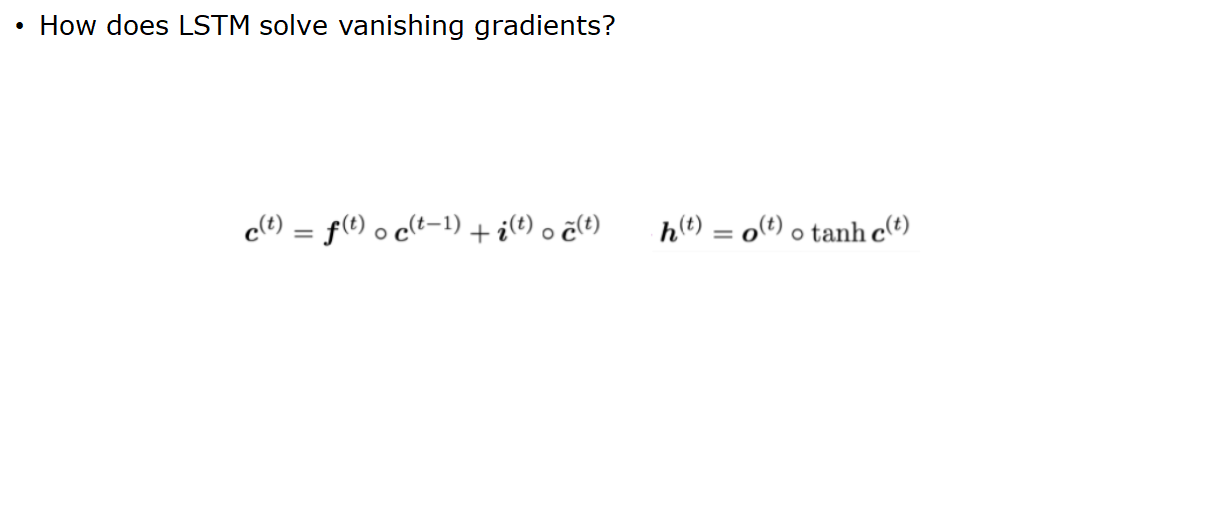
cell state에 대한 식이다. 수식을 살펴보면, forget gate가 1이고, input gate가 0 일때 Cell의 정보가 완전하게 보존되서 장기의존성 문제를 해결할 수 있게됨을 확인할 수 있음. 하지만 이처럼 1과 0으로 나타나지 않기 때문에 여전히 Gradient Vanishing의 완전한 해결을 보장하지는 않는다.
3.GRU
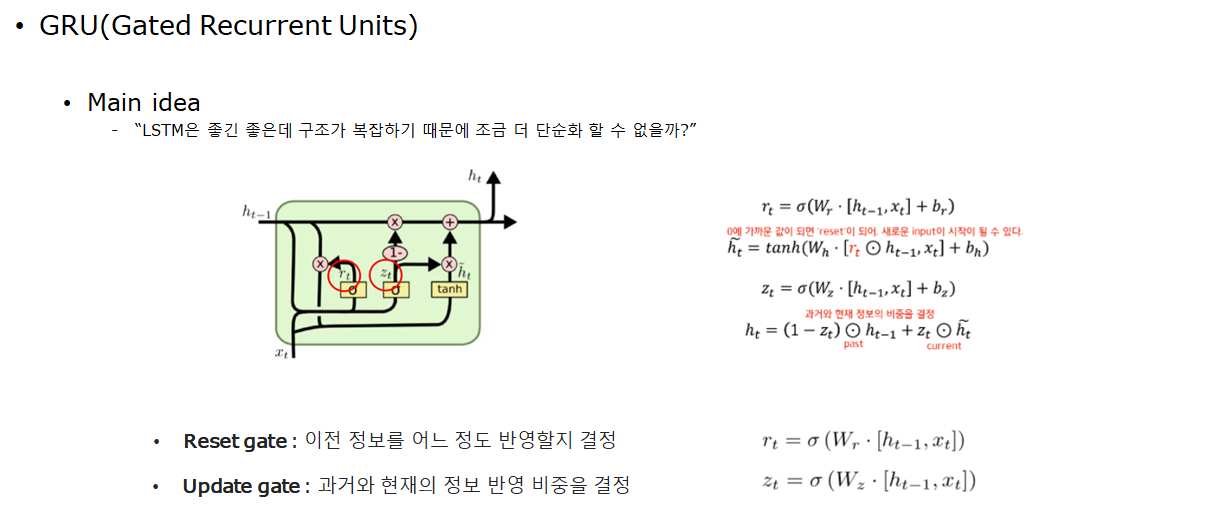
4.Fancy Rnns
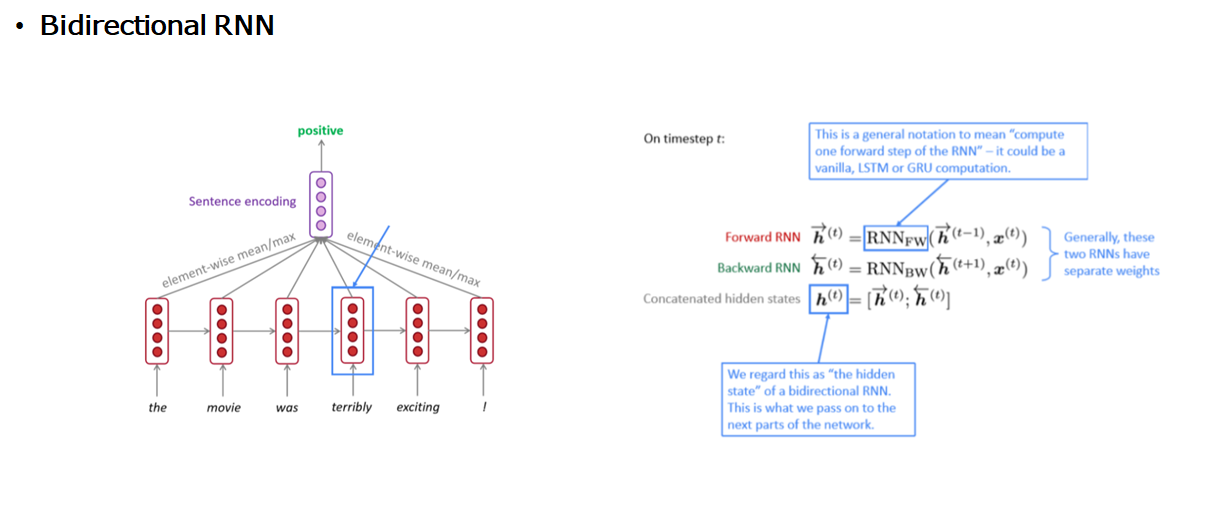
기존의 RNN은 forword방향으로만 학습을 진행하였습니다. 하지만 이는 과거의 상태에 의존하여 미래를 예측함으로 다소 오류가 발견될 수 있습니다. 이를 해결하고자 backword부분의 학습도 진행하여 미래의 상태까지 고려하는 모델입니다. 학습방법은 오른쪽과 같이 forward, backward 각각 훈련을 진행 한 후 마지막에 concatenate를 하는 방식으로 진행이 됩니다.
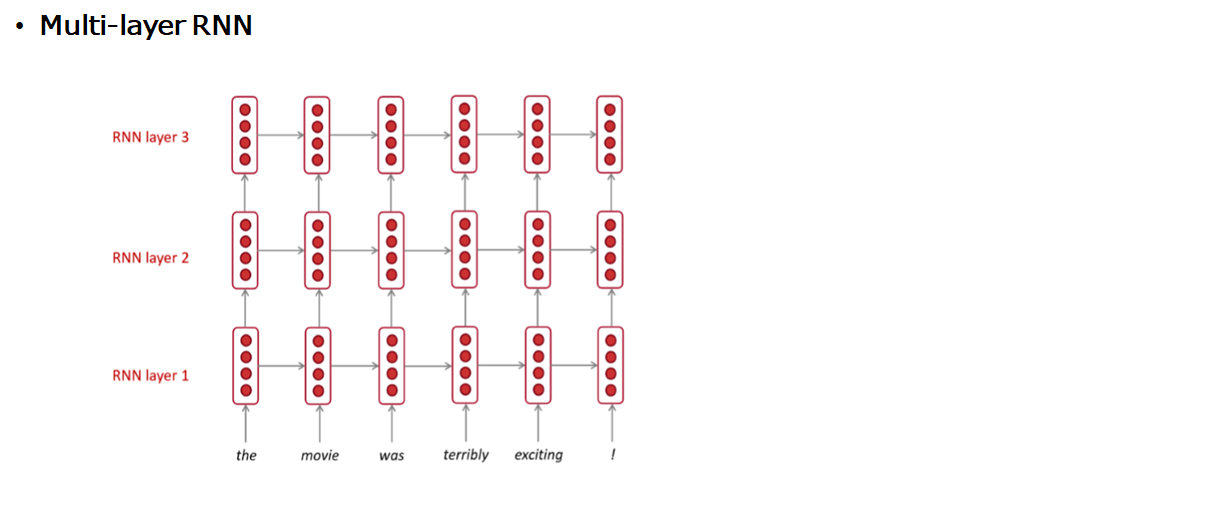
기존의 RNN을 여러 층으로 쌓은건데요 1번째 layer의 output이 두 번째 layer의 input으로 들어가는게 특징
Reference
https://velog.io/@tobigs-text1415/Lecture-7-Vanishing-Gradients-Fancy-RNNs
https://velog.io/@tobigs-text1314/CS224n-Lecture-7-Vanishing-Gradients-And-Fancy-RNNs
3개의 댓글
15기 김현지
Vanishing Gradient
- Gradient Problem: Backpropagation 시 gradient가 너무 작거나, 클 때 학습이 제대로 되지 않는 경우
LSTM
- Main idea: 과거 내용을 얼마나 잊을지 정하고, 현재 정보를 얼마나 더할지 정한다.
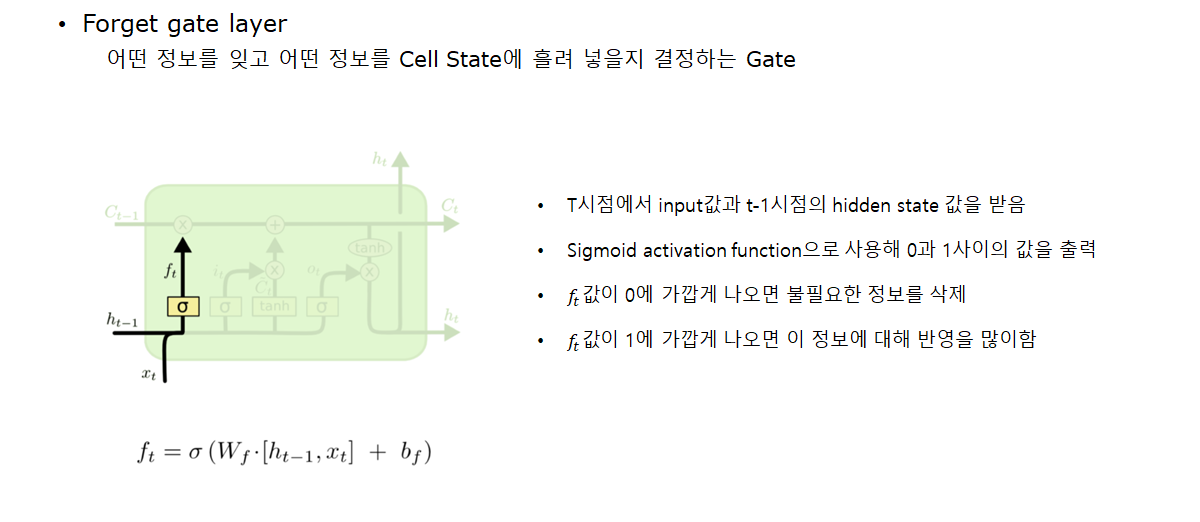
- Forget gate layer: 어떤 정보를 잊고 어떤 정보를 Cell State에 흘려 넣을 지 결정하는 Gate
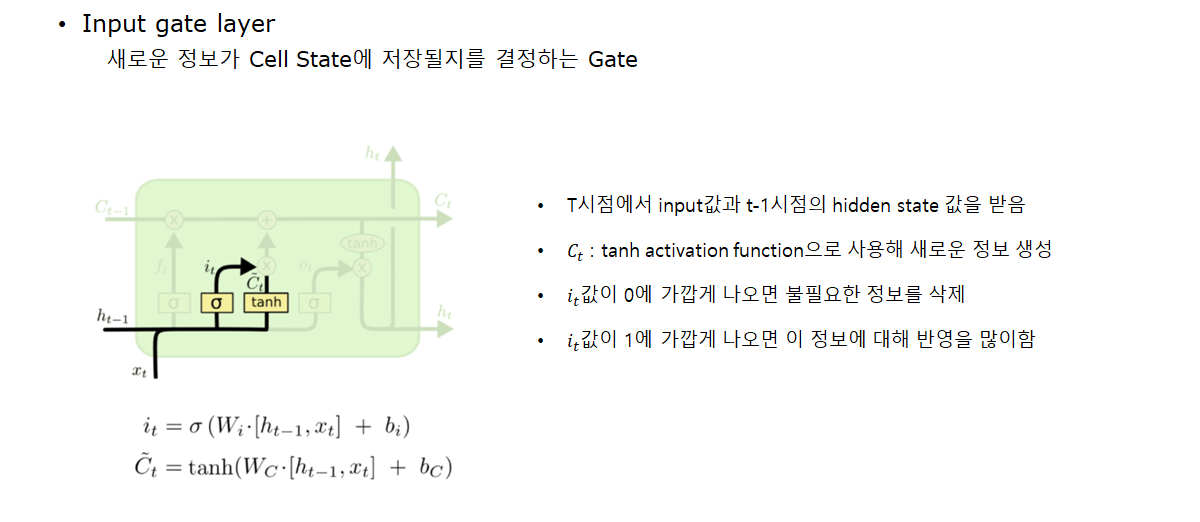
- Input gate layer: 새로운 정보가 Cell State에 저장될지를 결정하는 Gate
- Update & Output gate layer: 새로운 정보가 Cell State에 저장될지를 결정하는 Gate
- forget gate가 1이고, input gate가 0일 때 Cell의 정보가 완전하게 보존되어서 장기의존성 문제를 해결할 수 있지만, 이처럼 1과 0으로 나타나지 않기 때문에 여전히 Gradient Vanishing의 완전한 해결을 보장하지 않는다.
GRU
- LSTM에서 구조를 단순화한 모델
- 파라미터가 보다 적기 때문에 학습이 빨리된다.
Fancy Rnns
- Bidirectional RNN: forward 방향 뿐 아니라 backward 부분의 학습도 진행하여 미래의 상태까지 고려하는 모델
- Multi-layer RNN: 기존의 RNN을 여러 층으로 쌓은 모델
기본적인 RNN부터 GRU, Fancy RNN까지 깔끔하게 정리할 수 있는 세션이었습니다. 감사합니다!
16기 이승주
RNN
Vanishing Gradient problem for RNN
Backpropagation 시 gradient가 너무 작거나, 클 때 학습이 제대로 되지 않는 경우인 문제이다.
LSTM
Forget gate layer, Input gate layer, Update & Output gate layer의 역할은 gate들이 존재하여 RNN의 장기 의존성 문제를 일부 해결 가능하지만 여전히 한계점은 존재한다.
GRU
LSTM의 구조를 단순화한 모델이며 LSTM보다 파라미터가 작아 비슷한 성능을 내지만 학습이 빠르다.
Fancy Rnns
backword부분의 학습도 진행하여 미래의 상태까지 고려하는 모델이다. 학습방법은 오른쪽과 같이 forward, backward 각각 훈련을 진행 한 후 마지막에 concatenate를 하는 방식으로 진행이 된다.
좋은 강의 감사합니다.
16기 주지훈
Vanila RNN의 Vanishing Gradient Problem
LSTM
GRU
LSTM과 GRU 모두 장기 기억에 좋다. 그러나 기울기 소실 문제가 완전히 해결되지는 않았다.
Fancy RNNs
여러 종류의 RNN에 대해 배우면서 RNN에 대해 더 깊게 알 수 있었습니다. 유익한 발표 감사합니다:)