DRIT++: Diverse Image-to-Image Translation via Disentangled Representations

1. introduction

기존 I2I translation은 두 가지 문제점을 갖고 있다.

• image pair의 수집이 어렵다.
• many such mappings are inherently multimodal
  - single input에 대해 다수의 output이 존재할 가능성.
  

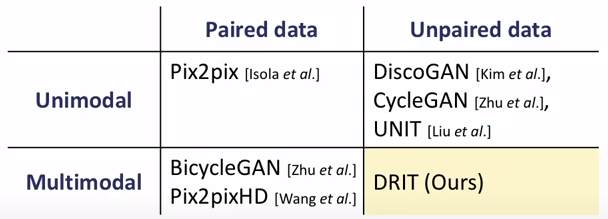
기존 genrator에 noise vector를 input으로 추가하는 방법들은 mode collapse issue로 인해 생성된 이미지들의 variation을 증가 시키지 못한다.(noise vector와 target domain 사이의 regularization이 부족해 multimodal generation에 부적합)

DRIT은 unpaired data의 조건에서 diverse output 생성을 위한 방법을 제안했다.

또한 Disentanglement representation을 content와 style을 분리하여 학습시킴으로써 실현했다.(넓은 의미의 disentanglement)

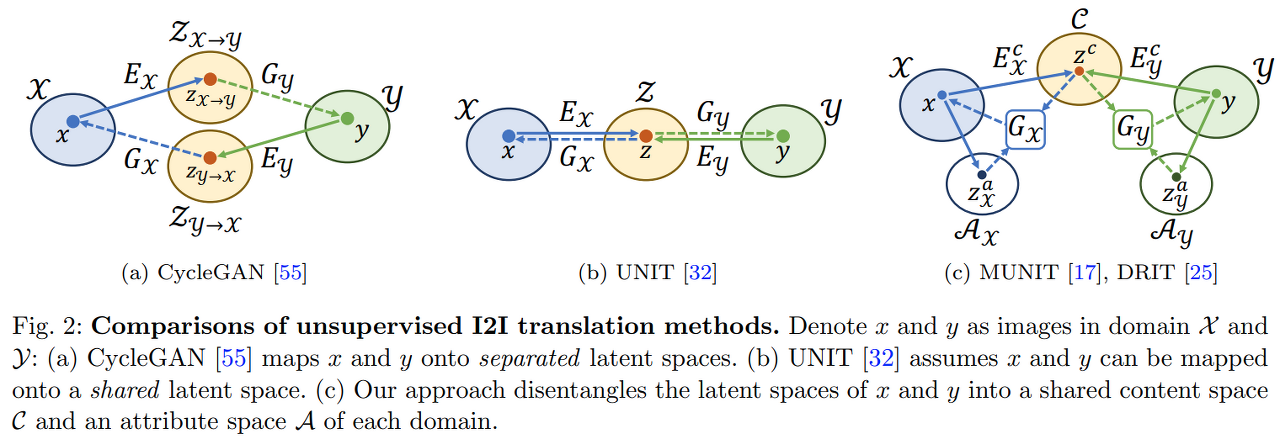
MUNIT과 DRIT의 구조가 매우 유사.
input image를 content와 attribute(style)로 구분해서 embedding한다는 점이 유사하다.

• MUNIT 구조
  

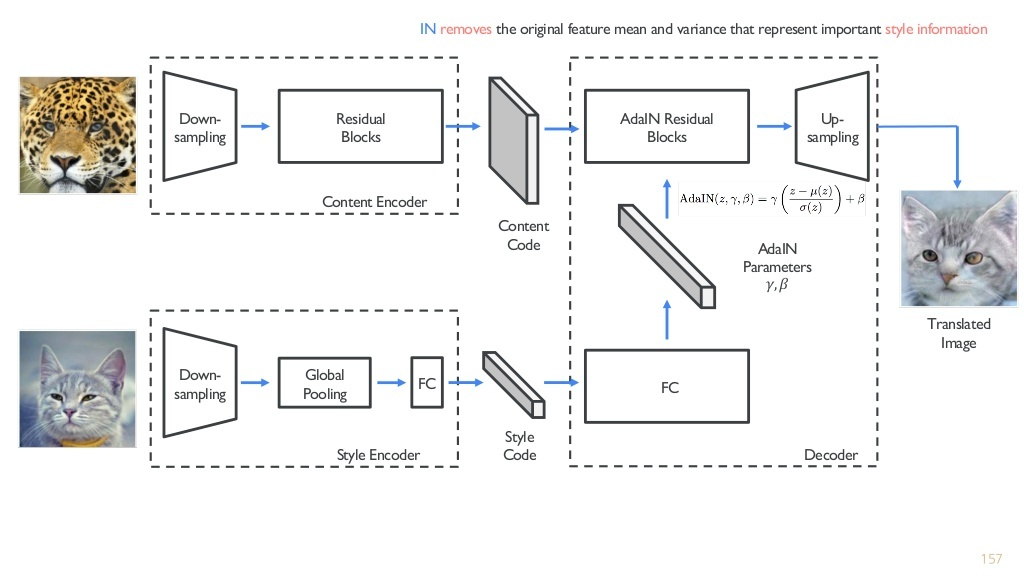
• DRIT 구조
  

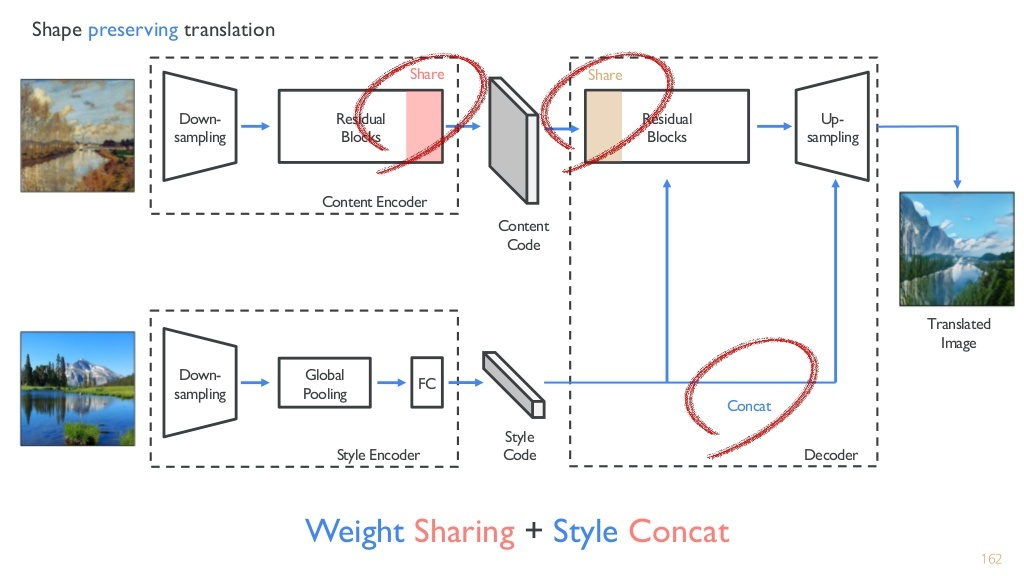
weight sharing과 style concat이 다르다.

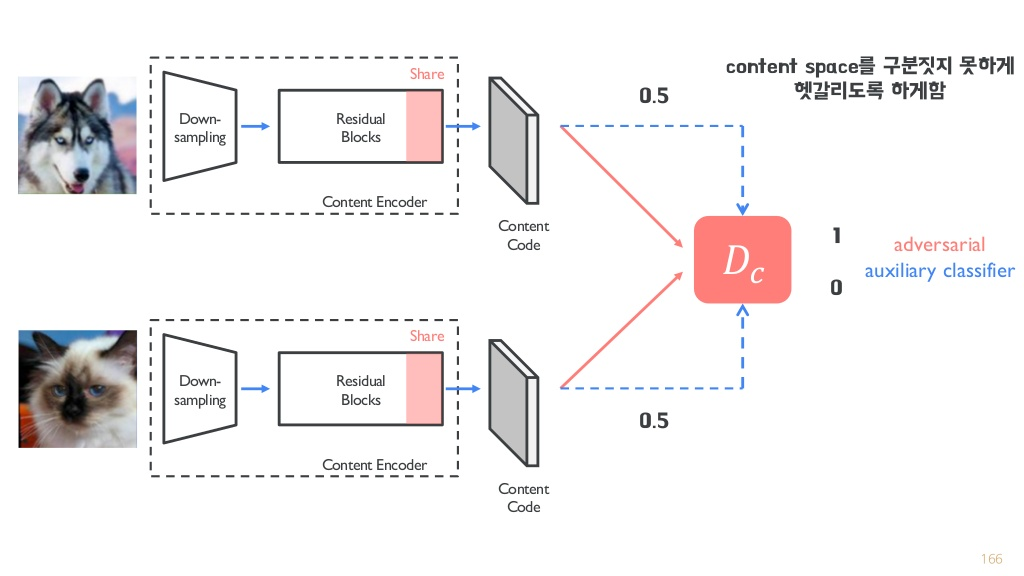
content discriminator가 존재하는 점도 다르다.

2. Disentangled Representation for I2I Translation

2.1 Disentangle Content and Attribute Representations

두 domain 사이에서 multi modal mapping의 학습을 목표로 한다.

-content encoders {$E_x^c$ , $E_y^c$ }와 attribute encoders {$E_x^a$ , $E_y^a$ }, generators {$G_x$ , $G_y$ }, domain discriminators {$D_x$ , $D_y$ }, content discriminators $D^c_{adv}$ 총 encoders 4개 generators 2개, discriminators 3개로구성

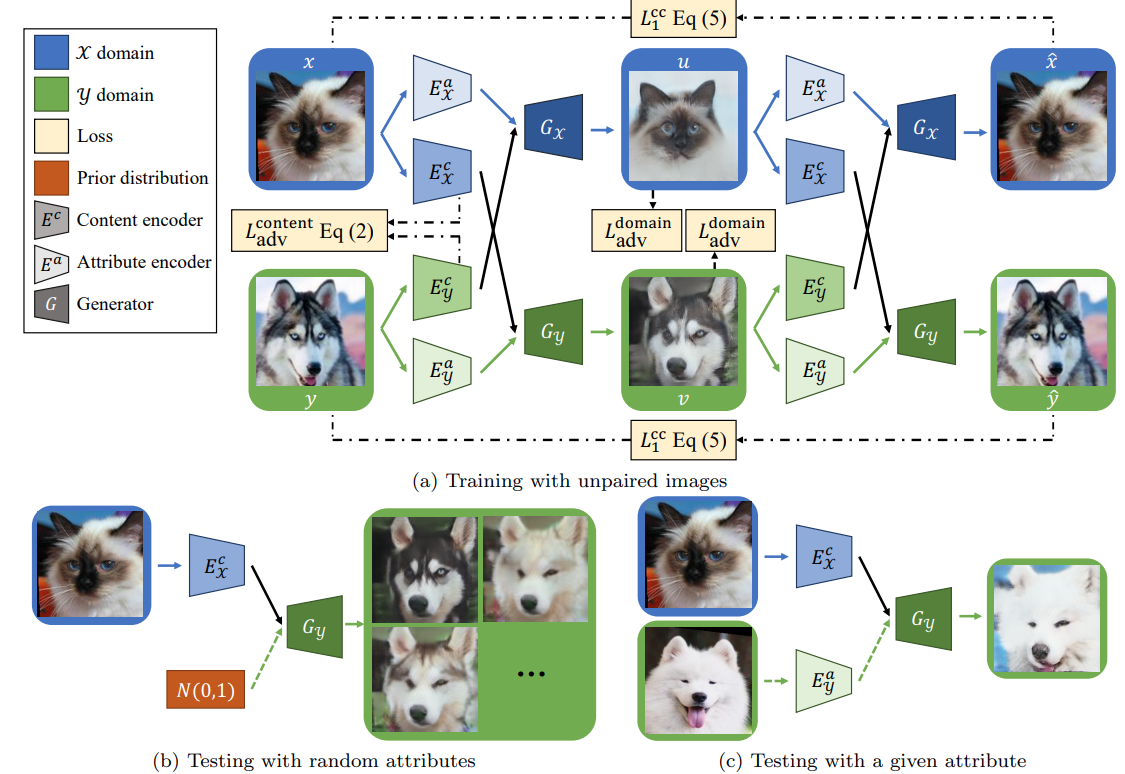
domain x를 예로 들면, 생성자는 style과 content 임베딩 벡터를 받아서 이미지를 합성한다.

판별자는 이미지가 실제인지 아닌지 판단해준다.

콘텐츠 판별자는 두 도메인 사이의 추출된 콘텐츠 표현을 구분하도록 학습된다.
-> disentanglement representation을 달성하기 위한 전략(+weight sharing)

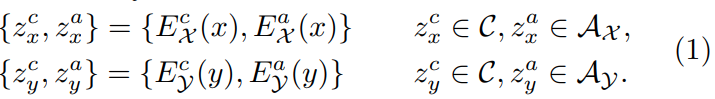
input image를 shared content space C, 그리고 domain-specific attribute space $A_x$, $A_y$로 임베딩 (content와 style로 나누어서 임베딩)

content -> image의 전반적인 내용
attribute(style) -> image의 세부적인 요소

content encoder는 space C상에서 도메인 간 공유 가능한 정보를 잘 임베딩 해야한다. (전반적인 내용은 공유하면서, 세부적인 요소를 다르게 이미지를 생성)
ex) 개/고양이 domain 간 자세, 표정은 공유 가능. 그러나 코, 눈 생김새, 고양이 수염 등은 특정 사진의 attribute로 임베딩 되어야함.

따라서 콘텐츠 임베딩을 동일 공간에 mapping하기 위해서 $E_x^c$ , $E_y^c$의 last layer와 $G_x$ , $G_y$의 first layer를 weigh sharing한다.

그러나 같은 mapping function이 동일 정보의 인코딩을 보장하지는 않는다.

따라서 content discriminator을 제안했다.
$D^c_{adv}$는 $z^c_x, z^c_y$를 구분할 수 있도록 하고, $E_x^c$ , $E_y^c$는 각 도메인을 구분할 수 없는 embedding을 만들도록 학습된다.

그러면 두 encoder는 동일 공간 상에 동일한 정보를 mapping하게 되고, 동일하지 않은 정보는 $E_x^a$ , $E_y^a$로 나눠진다.

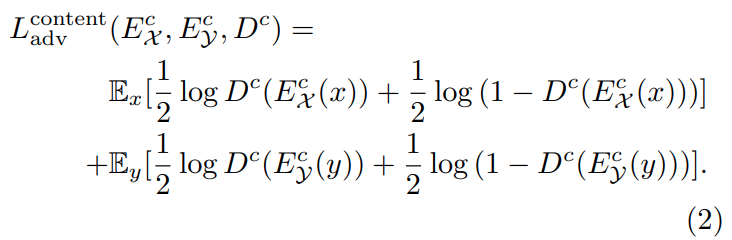
2.2 Cross-cycle Consistency Loss

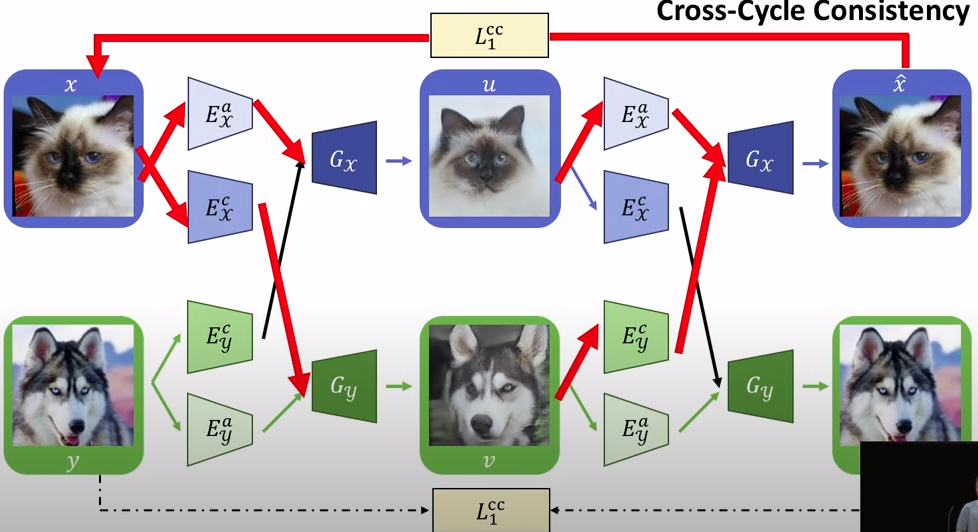
1. forward translation
   이미지 x, y가 주어지면 이를 각각 $\{{z_x}^c, {z_x}^a\}, \{{z_y}^c, {z_y}^a\}$ 으로 인코딩 시킨다. 그리고 ${z_x}^a, {z_y}^a$를 바꿔주고 생성자에 입력 시켜 이미지 u, v 생성 $u=G_x(z_y^c, z_x^a)$, $v=G_y(z_x^c, z_y^a)$

2. backward translation
   이미지 u, v가 주어지면 이를 각각 $\{{z_u}^c, {z_u}^a\}, \{{z_v}^c, {z_v}^a\}$으로 인코딩 시킨다. 그리고 두번째 translation으로서 ${z_u}^a, {z_v}^a$를 서로 바꿔주고 생성자에 입력하여 $\hat{x}$, $\hat{y}$을 생성

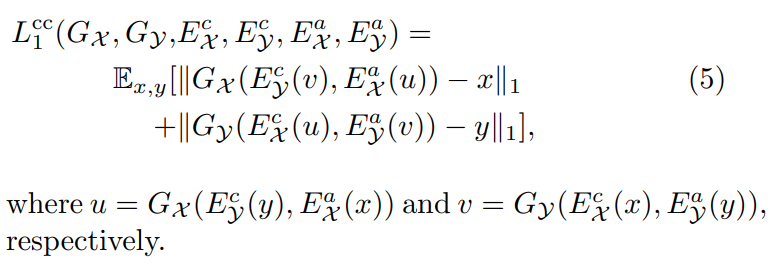
2.3 Other Loss Functions

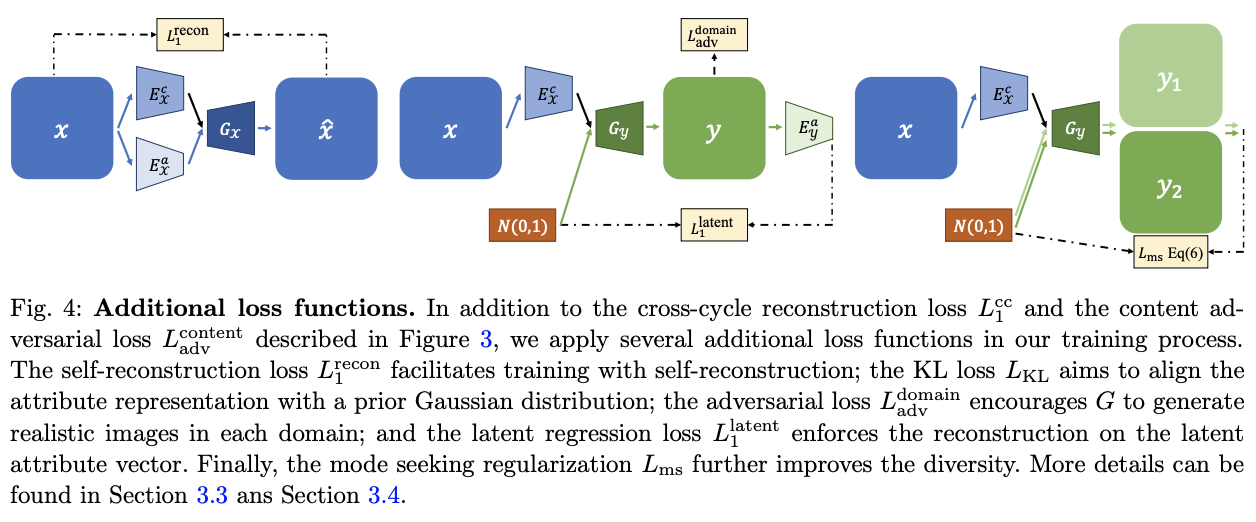
• self reconstruction : 훈련과정의 안정화 + KL loss 사용해 encoding 후 가우시안 prior에 embedding 되도록한다.
• Domain adversarial loss : 각각의 $D_x$와 $D_y$가 real과 fake를 구분하도록 학습하고 각 생성자는 실제와 같은 이미지를 생성시키도록 하는 일반적인 adversarial loss
• Latent regression loss : To encourage invertible mapping between the image and the latent space, we apply a latent regression loss L latent(새롭게 생성된 이미지에서 분리된 잠재 벡터가 원래 latent space(gaussian)에 잘 mapping 되도록)
  
  - self reconstruction : 이미지 latent vector -> gaussian
  - latent regression loss : gaussian에서 추출한 latent vector -> 이미지 latent vector

2.4 Mode Seeking Regularization

좀 더 다양한 image를 생성할 수 있도록 규제를 걸어주었다.
I = image

잠재 벡터의 거리가 가깝더라도 생성된 이미지는 최대한 다르도록 학습

---

DRIT 1
DRIT 2
DRIT 3
DRIT 코드참조

Beta-VAE

1. introduction

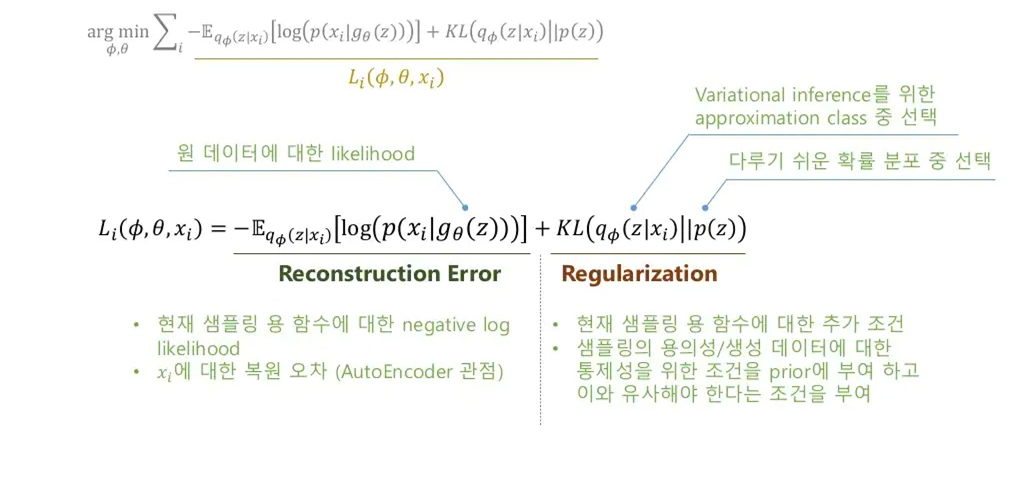
기존 vae의 loss는 sampling된 잠재 벡터에서 본래 이미지가 얼마나 잘 생성되는지에 대한 reconstruction error term과 생성 데이터에 대한 통제를 위해 잠재 벡터가 prior 분포를 따르도록 하는 regularization term을 포함한다.

beta-vae는 기존 vae의 regularization에 좀 더 강한 규제를 주는 것이다.

2. key idea

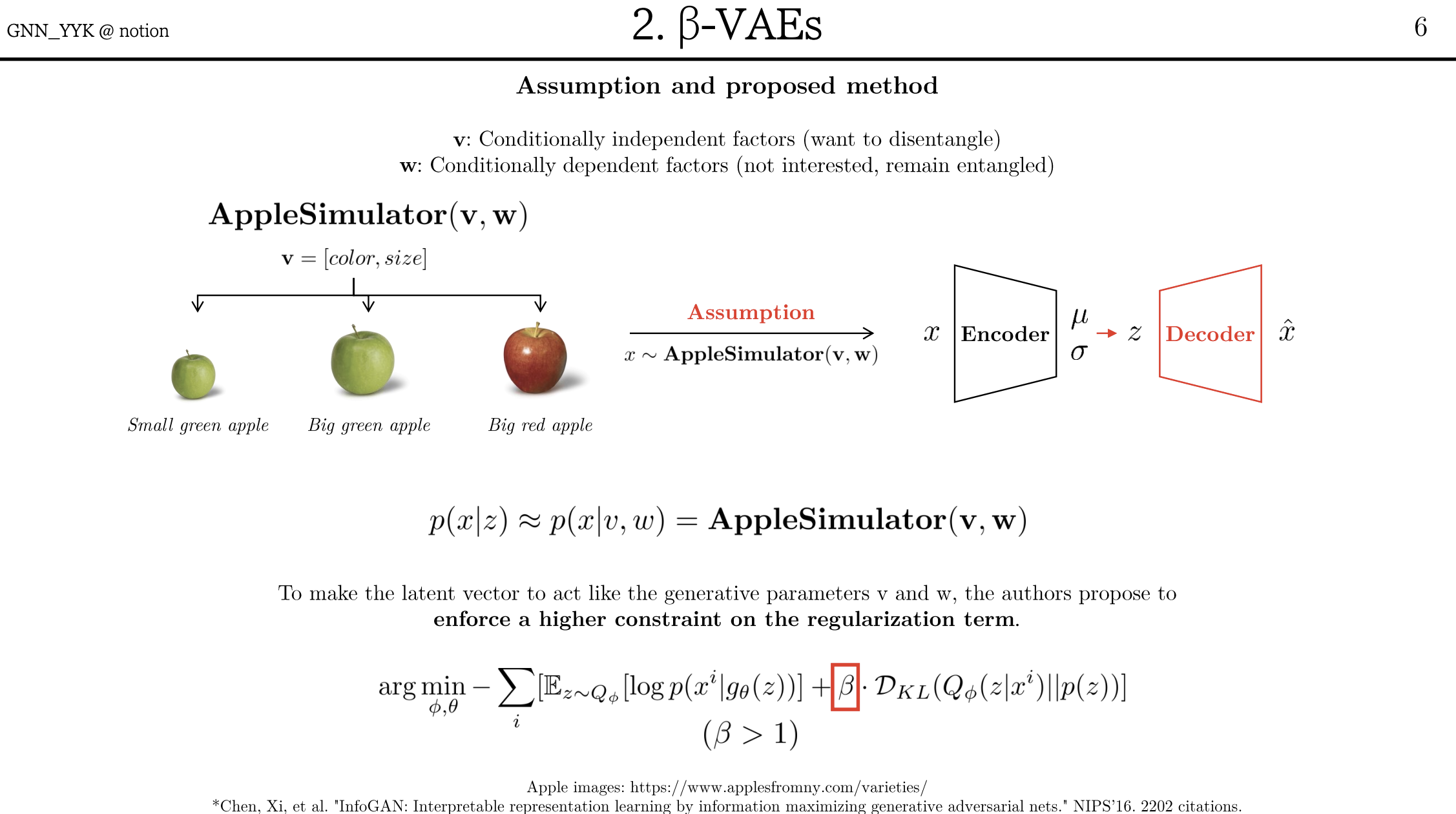
x: 이미지
v: conditionally independent factors
w: conditionally dependent factors
Sim() : 이미지 생성기 (저자는 simulator라고 표현)

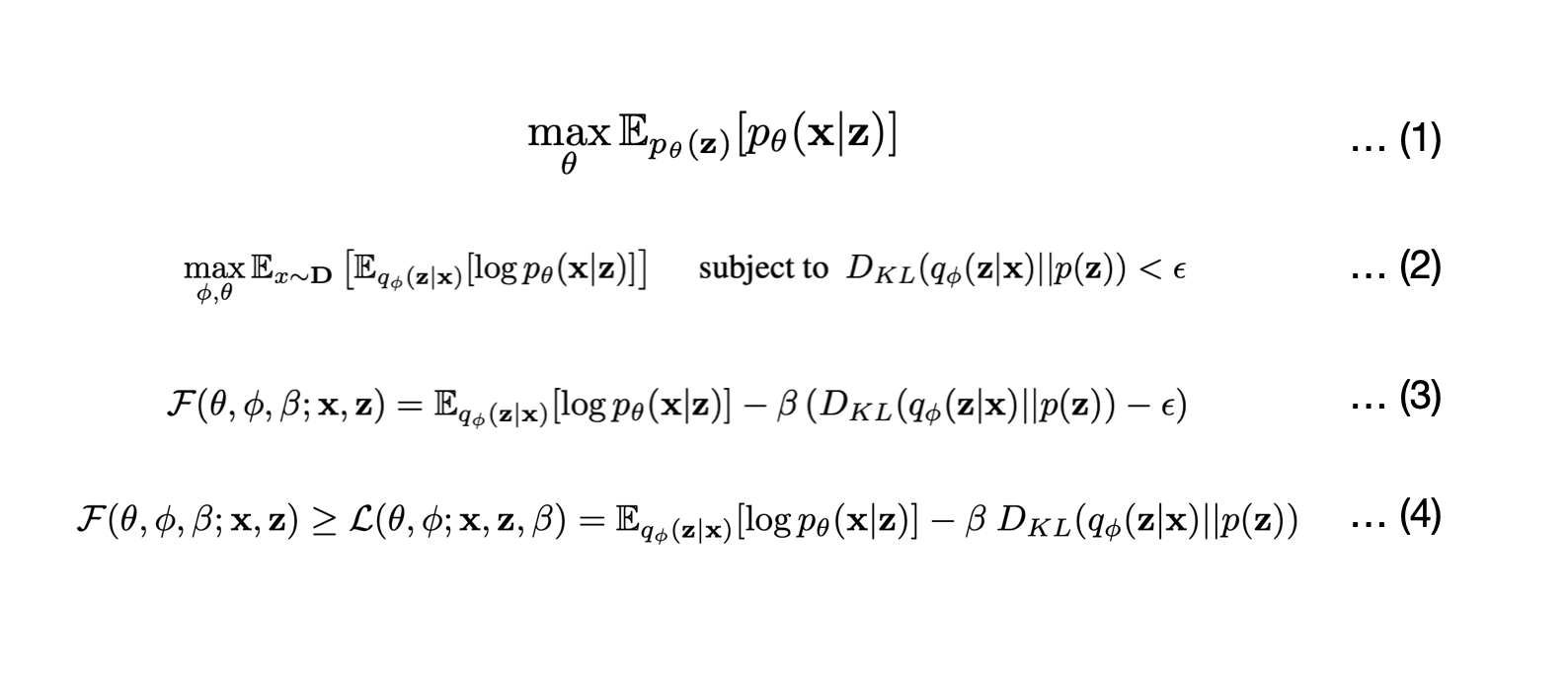
(1) 모델은 data x와 latent factors z의 결합 분포를 학습할 수 있다. (이 때 z는 x를 생성할 수 있는 factor) 즉, p(x∣z)≈p(x∣v,w)=Sim(v,w) 입니다. 따라서 수식(1)을 maximize해야한다.

(2) VAE에서 공부했듯이, $q_\phi(z∣x)$로부터 z의 분포를 추정한다.

중요한 것은, $q_\phi(z∣x)$가 disentanglement part인 v를 잘 capture해야한다는 것이다. v를 제외한 나머지 part가 w라고 생각할 수 있습니다. 이를 보장하기 위해,$q_\phi(z∣x)$가 p(z)와 match 되게끔 constraint을 걸게 된다.

이는 p(z)∼N(0,I)를 가정하면 조건부 최적화 문제로 풀 수 있다.

(3) 수식 (2)를 KKT 조건 하에 라그랑지안으로 풀면 (3)을 얻게 된다. (KKT 조건을 만족한다고 가정했기 때문에 (2)의 최적 솔루션이 (3)의 최적 솔루션을 구하는 것과 같음을 알 수 있다.)

여기서 KKT multiplier β는 latent information channel z를 통제하는 regularization coefficient가 된다.

(4) KKT 조건의 the complementary slackness(KKT 조건 중 하나)에 따라 ϵ ≥ 0이므로, 최종적으로 lower bound (4)가 나오게 됩니다.

beta의 역할:

• Disentanglementd의 정도를 조절할 수 있음.
• beta = 1, Vanila VAE와 동일함.
• beta > 1, 더 효율적인 latent representation을 찾기 위해 학습함. (regularize term이 강화됨.)
• 학습이 비교적 안정적임.
• 최종 목적식 (4)에서도 알 수 있듯이, 실제로 v, w는 가정일 뿐 conditionally independent factors v, conditionally dependent factors w에 관여하는 텀은 없다.

결국 제약조건으로 인해 등장한 β 텀을 잘 조절하며 학습하면, z가 v, w로 분해가 되는 것입니다.

즉, 기존 vae에서 KL term에 규제를 가해 잠재 벡터의 분포가 prior를 따르도록 더욱 강제하면 disentanglement가 잘 된다는 것이다.

->vae 기반이기 때문에 규제를 가하면서 정보 손실이 존재 ->blurry한 이미지 생성

3. Why it works?

3.1 Information bottleneck Theory

Information bottleneck이론이란 데이터 X로부터 관련 정보인 Y로 정보를 압축할 때 Y와의 관련성(accuracy)과 X의 압축성(compression)사이의 최고의 tradeoff를 정보량을 통하여 찾는 기법을 말한다.
$R_{IB}(\theta) = I(Z, Y; \theta) - \beta I(Z, X; \theta)$

따라서 beta vae 모델도 학습을 진행할 때, reconstruction quality(관련성) and KL-divergence(압축성) trade off가 발생한다.

잠재 벡터로 압축을 하면서, z의 차원 중 최소한의 z에 연관 정보를 모두 담게해야지 정보손실을 줄이면서 압축률을 높일 수 있다.

이를 위해선 distanglement되기 쉬운 특징들(이미 서로 independent한)을 압축된 잠재 벡터의 축에 할당하는 것이 정보 손실이 적다.

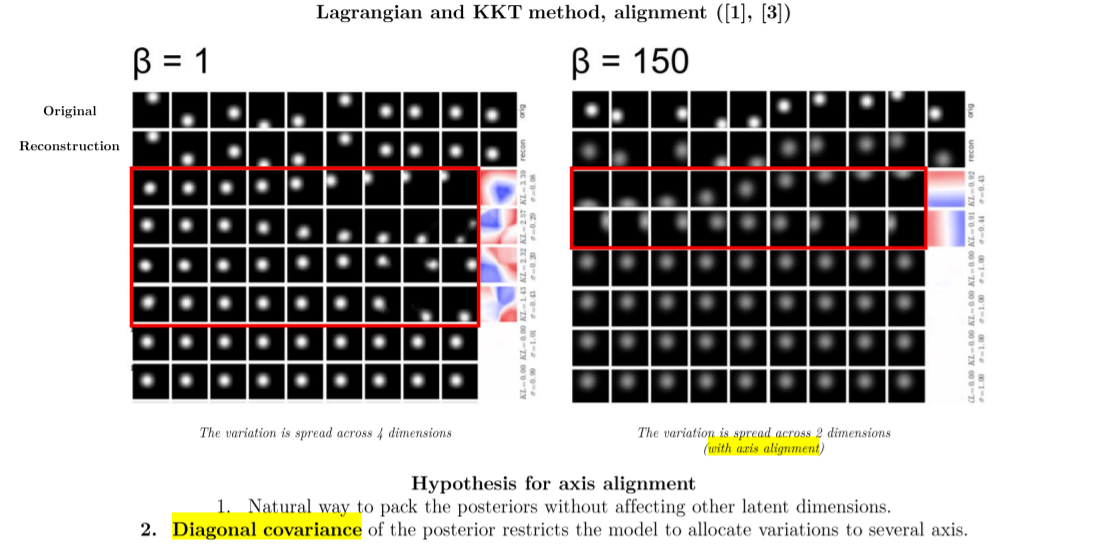
beta-VAE aligns latent dimensions with components that make different contributions to reconstruction

이에 따라 distanglement 되는 순서도 reconstruction에 큰 영향을 주는(정보 이득이 가장 큰->정보 손실이 적은 특징 distangling 되었다는 뜻 -> 이미 independent한 ->여기선 x,y axis가 해당) 순서대로 distangling 된다.

그러나 이러한 방식으로 잠재벡터에 할당된 특징이 항상 "correct"한가?
(independent -> human-understandable을 보장?)

https://arxiv.org/pdf/1812.02833.pdf
-beta-vae가 distanglement를 강제하지 않는다는 주장

https://arxiv.org/pdf/1812.06775.pdf
-mean field assumption이 latent의 독립성에 기여한다는 주장
(beta-vae는 독립성에 효과가 없다??)

->emphrical한 결과

---

beta vae1

beta vae2

beta vae3

beta vae4