- 카르노 맵 POS 혹은 SOP 표현 방법
https://optimuslee.tistory.com/21
6 논리식의 간소화
카르노 맵은 1953년 모리스 카르노가 소개하였습니다. 카르노 맵은 함수에서 사용할 최소항들을 각 칸 안에 넣어서 표로 만들어 놓은 것이다. 2변수일 때는 4개, 3변수일때는 8개, 4변수일 때는 16개의 칸이 필요하다.
변수가 5개, 6개 정도 되면은 힘들지만 추후에 나올 Quinne-Mckluskey는 5개 이상의 변수에서도 할 수 가 있다. 하지만 카르노 맵이 좀 더 보고 이해하기 쉬워서 사용하는 편이다.
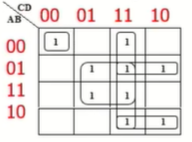
위의 그래프에서는 9개의 minterm에 대한 graphical한 map의 position에 1을 적어 놨음. 이때 입력 값들은 오로지 1비트만 차이 나도록 만들어 놓았음. 이때 묶어놓은 숫자들을 보면은 CD가 11인 경우에 대해서 묶어 놓거나 AB가 01 혹은 10인 경우에 대해서 묶어 놓았다는 것을 확인할 수 있다.
카르노 맵은 다음의 규칙을 따른다.
- Implicant : 2^k개의 1의 묶음(1,2,4,8...)
- Prime Implicant(PI) : 다른 implicant와 묶일 수 없는 implicant를 이야기 한다. 최대한 크게 묶는다.(더 큰 묶음에 포함되는 것은 없음) - 최대한 적은 숫자의 직사각형이 존재
하지만 PI는 묶다 보면 어쩔 수 없이 비트 일부가 다른 PI 들과도 묶여서 전체 비트가 서로 다른 PI와 묶여 있는 경우가 생길 수 있다. - Essential prime Implicant(EPI) : 이제 묶다 보면 다른 사각형하고 묶이게 될텐데 적어도 하나의 비트가 다른 사각형에 들어가지 않은 Implicant를 EPI라고 부른다. 또한 또 다른 묶는 방법이 존재하지 않아야 한다.
그래서 EPI->PI 이지만 PI->EPI 인 것은 아니다. 그렇기에 Implicant 와 PI 규칙을 만족하는데도 비트가 남는 것만이 EPI 이다. 자세한건 디지털 회로개론 9에서 다룬다.
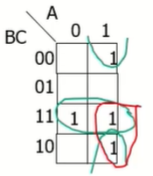
또 다른 예제를 보자 위와 같은 진리표는 PI가 3개가 나올 수 있으며 EPI 가 2개이다.
이때 가로로 놔 있는 친구는 BC / 세로로 놔 있는 초록섹 친구는 AC' / 세로로 놔 있는 빨간색 친구는 AB로 놓을 수 있다. 하지만 EPI만 존재하여도 모든 비트를 관리할 수 있기 때문에 AB는 사실상 반드시 필요한 Implicant라고 생각할 수 없다.

최적화 알고리즘
- 모든 PI를 찾기
- 모든 EPI를 찾기
- 무존건 EPI로 구성한다음 남은 비트를 해결하기 위해 PI를 사용
6.1 2변수 카르노 맵
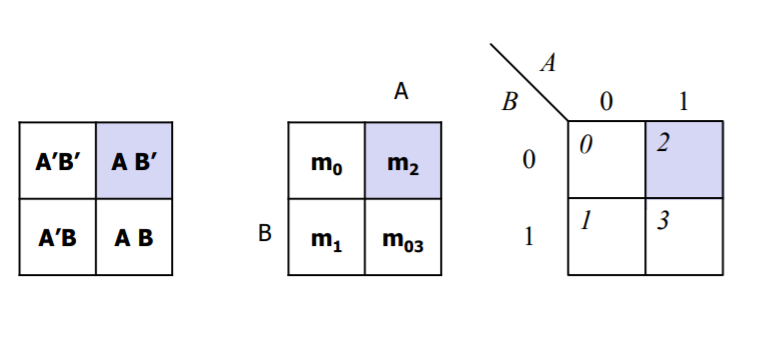
위와 같이 입력값이 1인 곳을 표시하고, 0인 곳은 비어놓거나 0으로 표시하고 이를 또 minterm으로 생각하여 각 칸에 번호를 붙일 수도 있다. 그리고 만약 해당칸이 출력에 미치는 영향이 없다면 'x'를 붙이어 놓기도 한다.
6.2 3변수 카르노 맵
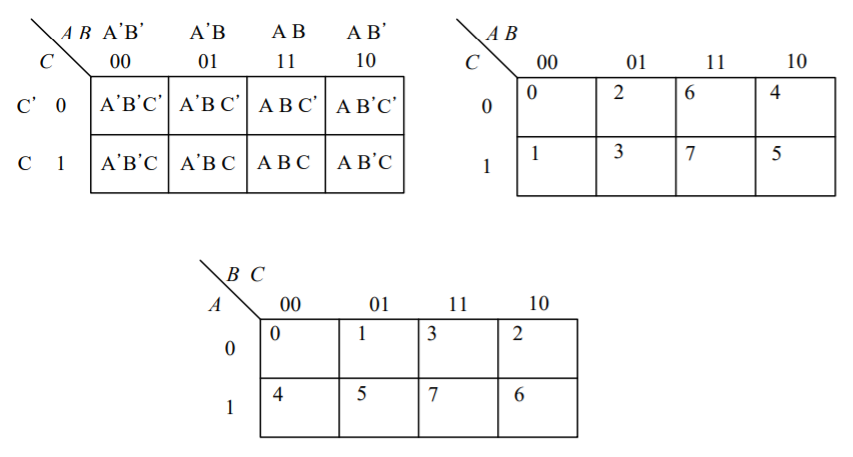
이때 minterm 번호는 위와 같이 매기어 진다. 보면 알겠지만 번호가 매기어 지는 것은 순서대로가 아니다.
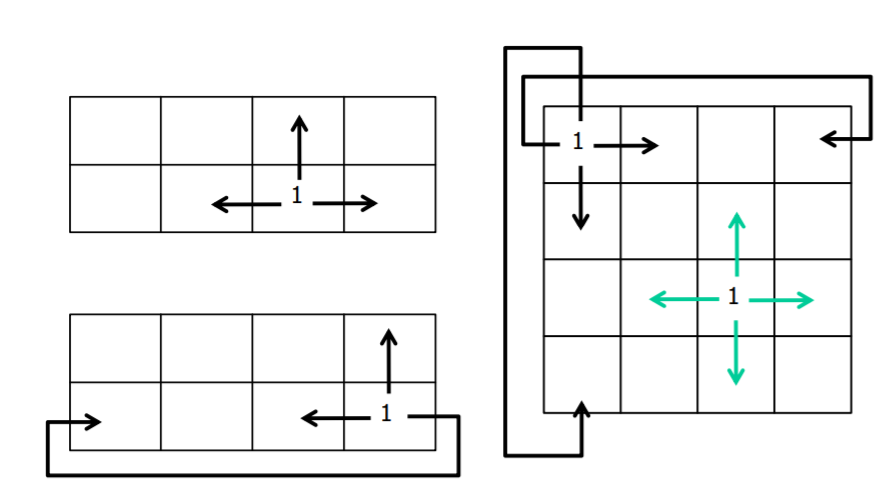
그러면 각 위치에서의 값들은 누구와 neighbor일까? 이는 바로 위와 같은 표의 형태를 띄게 된다. 위와 같이 칸을 넘어서 반대편까지도 갈 수 있다.
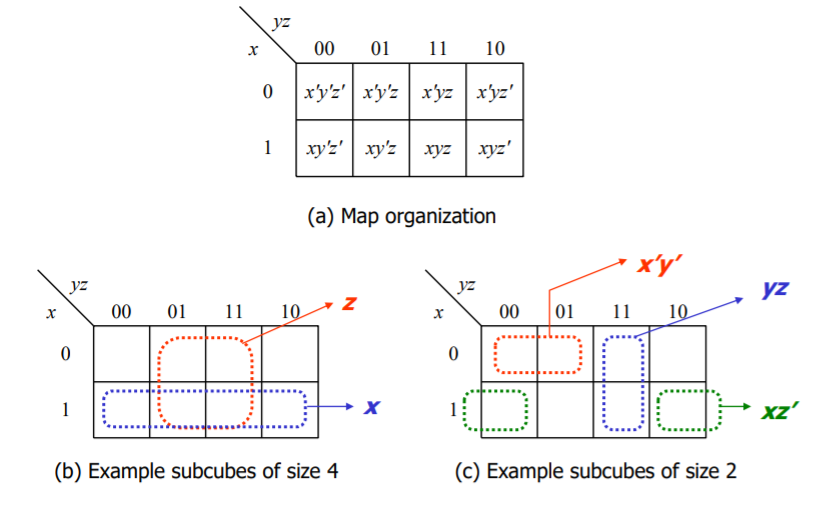
최종적으로 3변수 카르노 맵은 위와 같이 묶어서 구성할 수 있을 것이다.
3변수 카르노 맵 예제
가장 대표적인 3변수 카르노 맵 예제로는 전가산기가 존재한다.
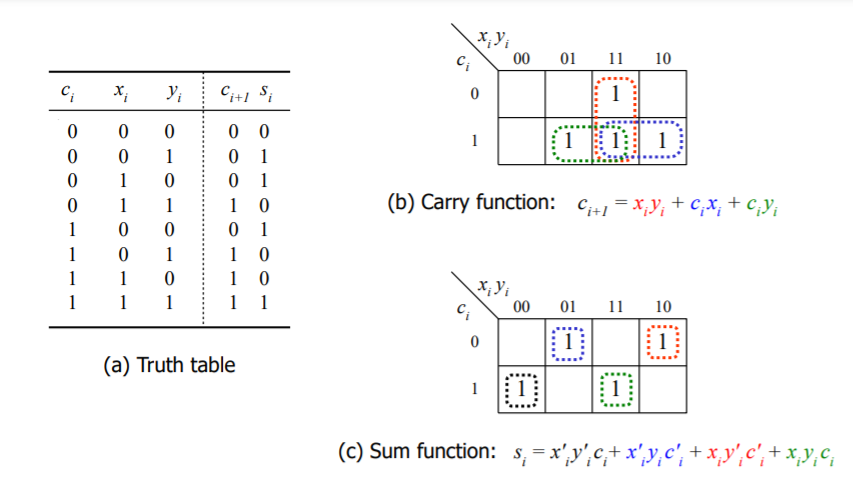
전가산기는 위와 같이 Carry와 Sum으로 나뉘어서 카르노 맵을 그릴 수 있다. Carry와 같은 경우 모두 EPI인 것을 확인할 수 있다. 반면에 Sum은 모두 PI인 매우 다른 결과가 나온 것을 볼 수 있다.
