생각정리. Boolean Function을 만들꺼면 최대한 크게 만들면 되고
EPI를 찾을꺼면 만들 수 있는 어떤 Implicant에 속하지 않는 PI를 모두 찾고 가장 큰 사각형들을 골라내면 결국 EPI가 나옴
6.2 3변수 카르노 맵
예를 들어서
x'yz'+x'yz+xy'z'+xy'z+xyz 가 있다고 하면 다음과 같이 묶으면 된다.
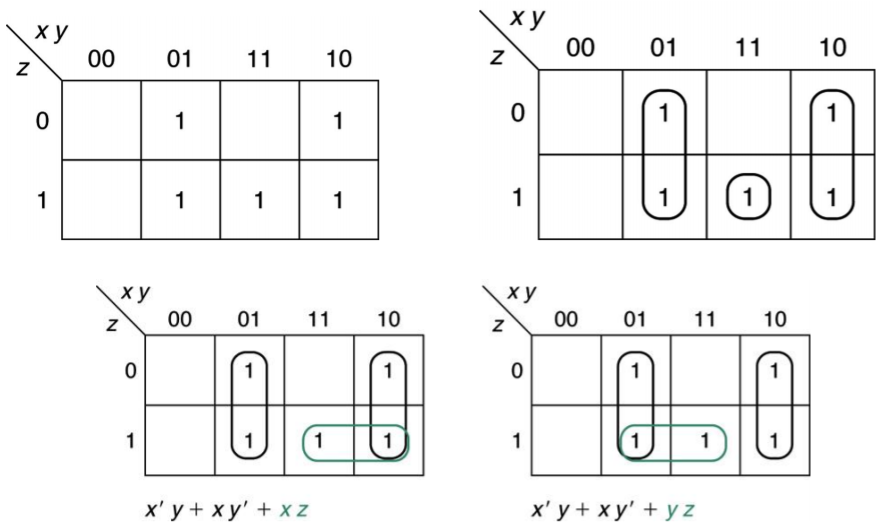
2번 방법은 PI가 아님에도 따로 남기어 두었기 때문에 제대로 Implicant를 구성하였다고 볼 수 없다.
3, 4번은 다시금 생각해 보면 3과 4의 두 가지 방법으로 묶이기 때문에 essential 하다고는 볼 수 없다.
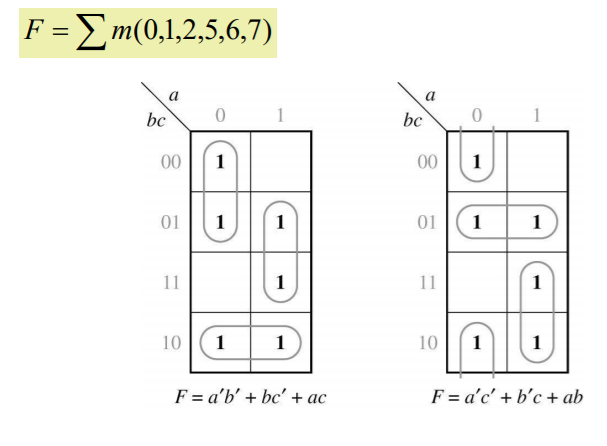
비슷하게 위의 경우도 묶일 수 있는 경우들을 모두 생각하여 보면 결코 Essential이 존재한다고 볼 수 없다.
6.3 4변수 카르노 맵
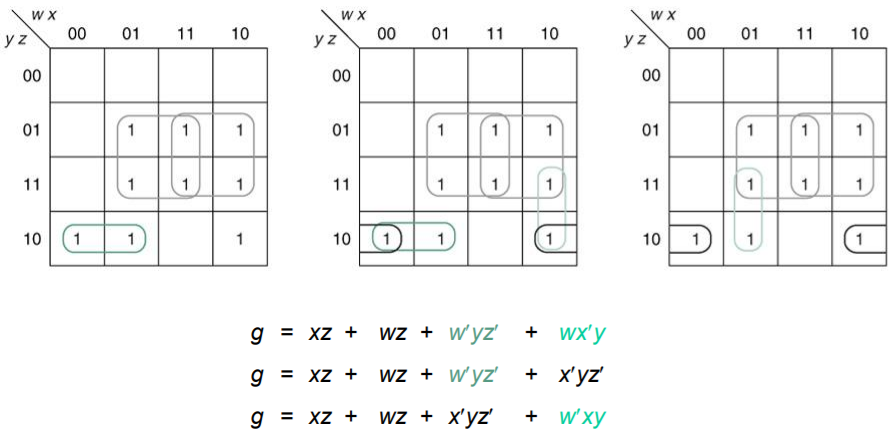
왼쪽 정사각형은 왼쪽 위의 1 때문에 Essential이다. 반대로 오른쪽 정사각형은 오른쪽 위의 1 때문에 Essential이다.
정리하자면 EPI는 Implicant와 PI 규칙을 만족하면서 남는 비트가 단 하나라도 존재하여야만 한다. 그래야만 위와 같이 절때 변하지 않는 xz+wz와 같은 식이 생길 수 있다.
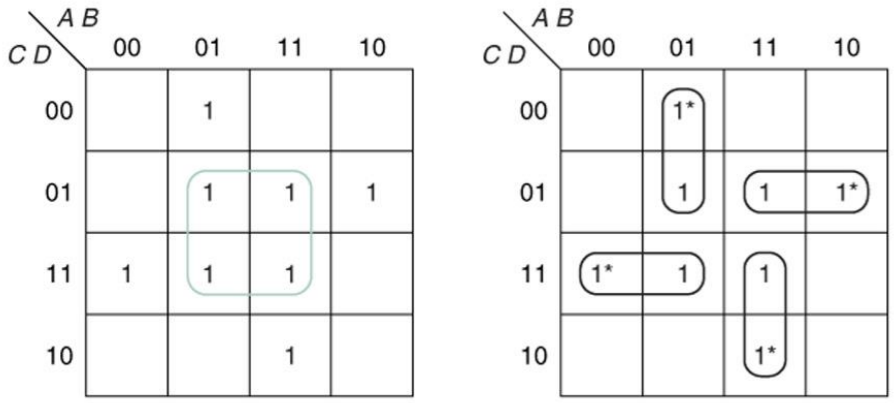
위와 같은 경우는 오른쪽과 같은 경우가 오히려 EPI이다. 그렇기에 가운데에 있던 사각형은 PI이 이다. 앞으로 많은 카르노 맵을 만들게 되겠지만 가급적 EPI를 많이 만들 수 있는 방향으로 진행하는 것이 좋다.
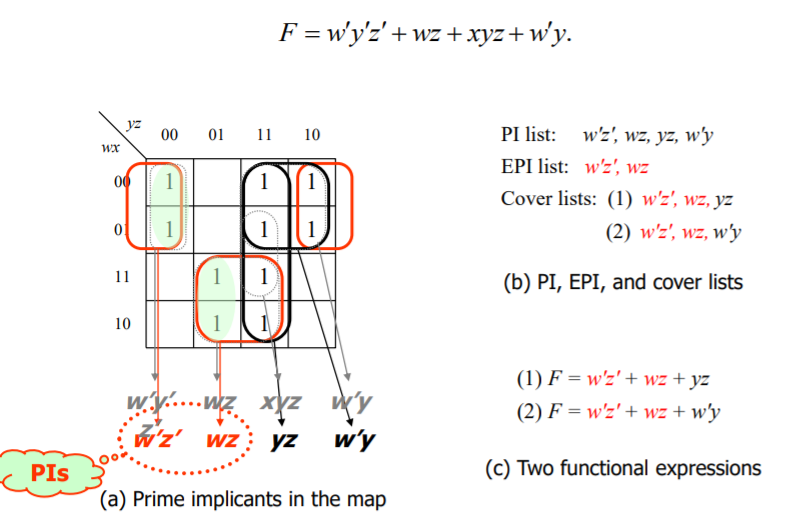
다른 하나를 가지고 연습하여 보자. 이번에느 EPI를 쉽게 얻어내기 위해 나올 수 있는 PI의 경우를 모두 찾아내였다.
그 결과 EPI로 나올 수 있는 것은 w'z'과 wz라는 것을 알 수 있게 되었다.
6.6 5변수, 6변수 카르노 맵
5변수 카르노 맵은 이제 하나의 변수를 기준으로 4변수 카르노 맵으로 나누어야 한다.
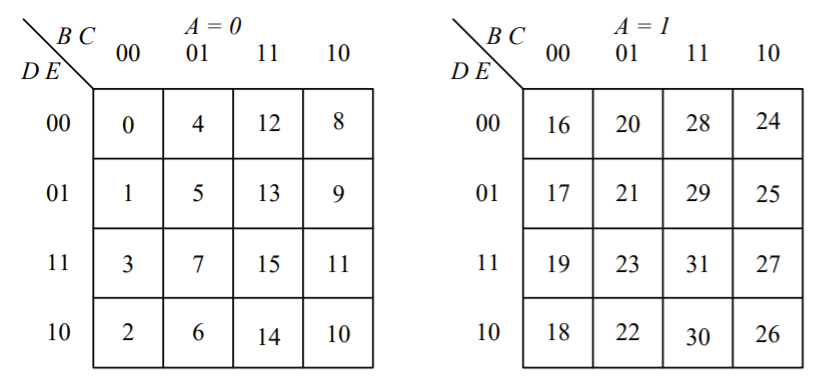
이제 기존과 가장 크게 다른점은 이게 3차원이라는 것이다! 그래서 3차원 적으로 묶일 수 있는 것을 추가로 묶어주어야만 한다.
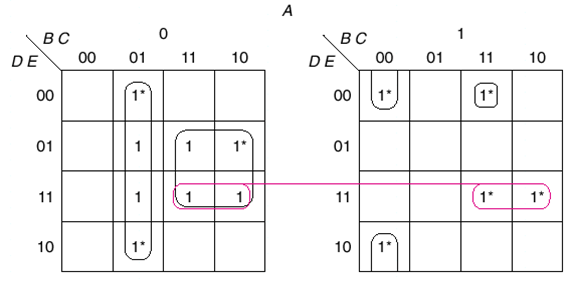
얘를 들면 이런식으로 말이다. 같은 위치에 있는 숫자끼리만 묶어 줄 수 있으며 이 경우 A는 0과 1 모두 되기 때문에 실재 수식 중 하나는 A가 빠진 결과물이 나오게 될 것이다.
카르노맵에서 SOP, POS 를 찾는 방법
이제 SOP 를 찾기 위해 minterm을 찾는 것은 쉽다 원래의 카르노 맵을 이용하면 되니
하지만 POS를 찾기 위해 Maxterm을 찾는 것은 어려운 일이다. 그래서 이 경우에는 0을 카르노 맵으로 모두 묶어서 F'을 우선 구한다. 그리고 여기에 드모르간의 법칙을 적용하여 F를 구하면 POS가 나오게 된다.
| YZ | 00 | 01 | 11 | 10 | |
|---|---|---|---|---|---|
| WX | 00 | 1 | 0 | 1 | 1 |
| 01 | 1 | 0 | 1 | 1 | |
| 11 | 0 | 1 | 1 | 0 | |
| 10 | 0 | 1 | 1 | 0 |
위와 같은 카르노 맵이 존재한다고 하였을 때 0끼리만 묶어 다음의 식을 구할 수 있다.
F' = w'y'z+wz'
이 식에 드모르간의 법칙을 적용하는 것이다.
(F')' = (w'y'z+wz')'=((w'y'z)'(wz')')=(w+y+z')(w'+z) = F
그렇다면 SOP는 언제쓰고 POS는 언제 사용하여야 하는 것일까? 이건 두개의 사례를 모두 해보고 게이트의 갯수를 보고 결정할 수도 있고 혹은 속도적 측면으로 생각하여서 결정할 수도 있다.
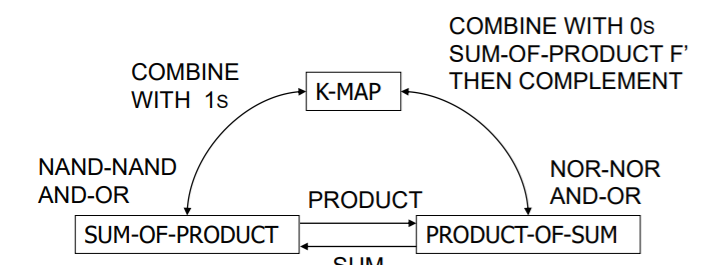
정리하면 앞에서 나온 위의 그림이 결과물이라고 생각할 수 있다.
NAND와 NOR 만의 게이트로 구성하기
이건 쉽게 이야기 해서 위의 영상을 보면 되는데 정리하면
1. NAND와 NOR만으로 NOT을 만들 수 있다.
2. AND앞에 not을 붙이면 NAND가 되고 뒤에 붙이면 NOR이 된다. 즉 앞에 not이 붙으면 같은 게이트 +NOT 뒤에 붙으면 정반대 게이트 +NOT 이 된다.
