6.4. 선택적 카르노 맵(k-map with Don't Cares)

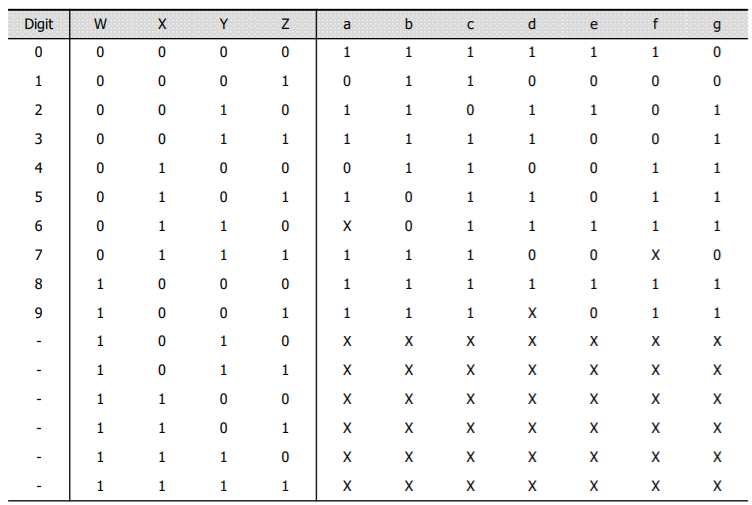
세븐 세그먼트를 보면 중간 중간 x가 있는 것을 볼 수 있다. 이것은 이 곳에 0 또는 1이 들어와도 상관이 없다는 표시이다.

혹은 digit가 없어서 dont care 처리한 것도 확인할 수 있다.

그래서 dont care의 조건은

• 그러한 minterm이 발생하지 않는 경우.(세븐 세그먼트에서 digit가 없는 경우를 들 수 있다.)
• 출력 값이 만들어지지만 사용되지 않는 것을 이야기 한다. 혹은 세븐 세그먼트 숫자 6의 a 출력은 사용되든 안되든 상관이 없는 것과 같은 경우를 이야기 한다.

그렇다면 dont care은 왜 사용하고 왜 logic optimization에 도움을 주는 것일까?

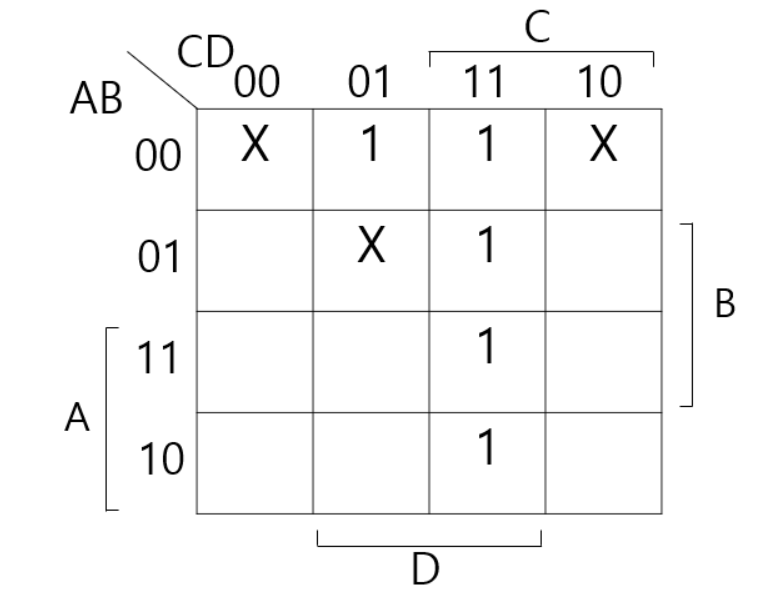
만약 다음과 같이 적히어져 있을 때 x자체는 큰 도움이 되지 않는 것처럼 보인다. 하지만 x까지 implicant를 묶게 된다면 그 이야기가 달라진다. 원래라면 해보았자 작은 사각형 두개가 생기어 F=A'B'D+CD가 되었을 터이지만

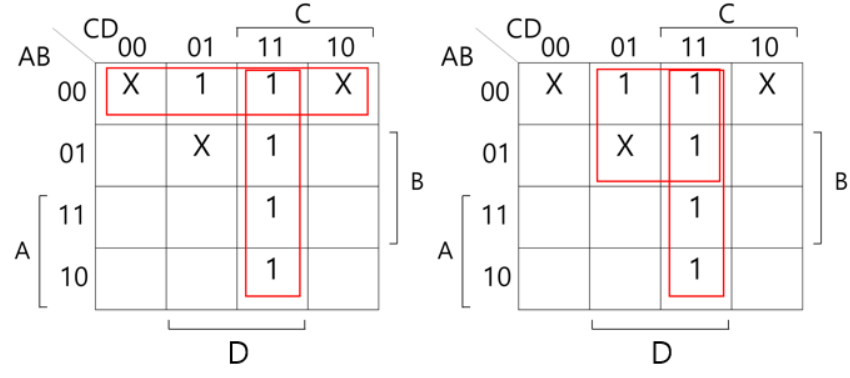
묶는 것에 따라서 F=A'B'+CD 혹은 F=A'D+CD 형태로 위의 식과 다르게 사용하는 변수 하나가 준 것을 확인할 수 있다. 이는 사각형의 크기가 기존과 다르게 커진것으로 생긴 logic optimization 기능이라고 볼 수 있다.

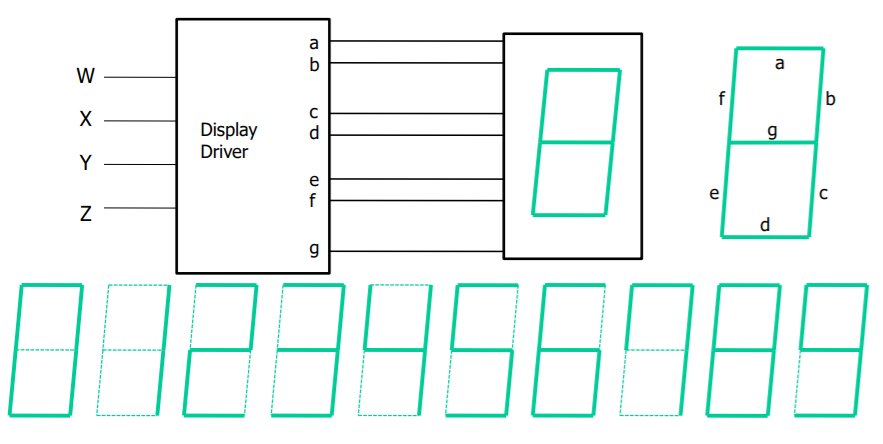
A seven-segment display

7. Designing Combinational Systems(조합논리회로)

7.1 가산기

1. 반가산기
   논리식
   s=a⊕b
   c=ab

2. 전가산기
   s=(a⊕b)⊕c
   c=(a⊕b)c+ab

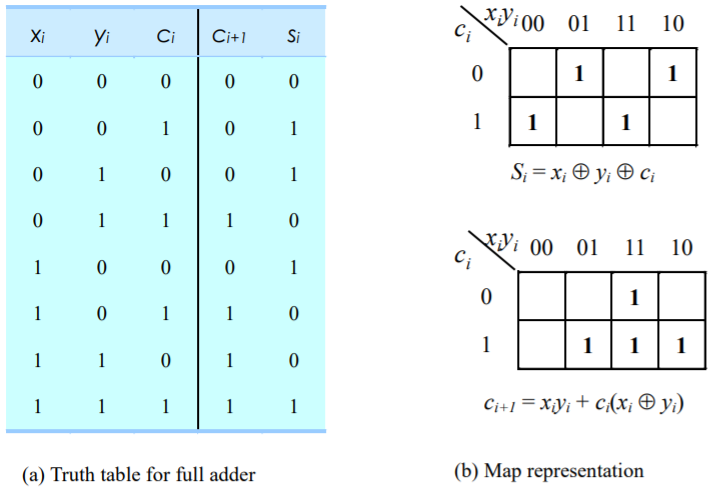
전가산기는 위와 같이 진리표와 불리안 식을 가지게 된다.

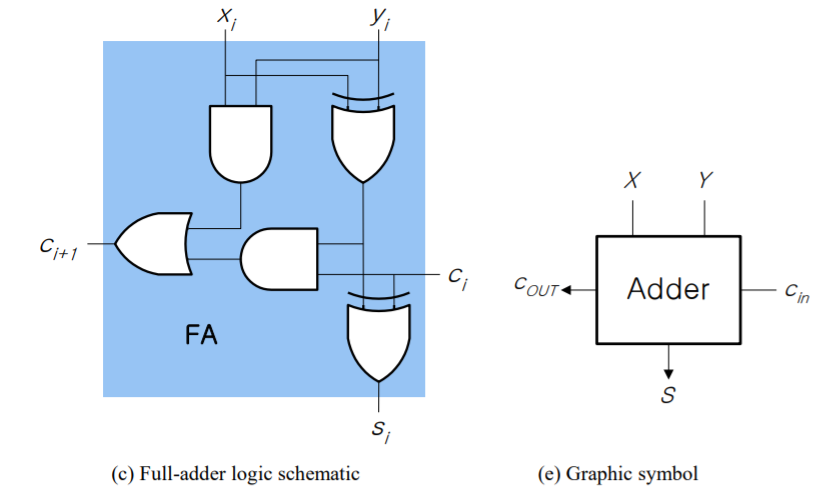
그래서 위의 식의 회로도를 구성하면 위와 같이 생성된다.

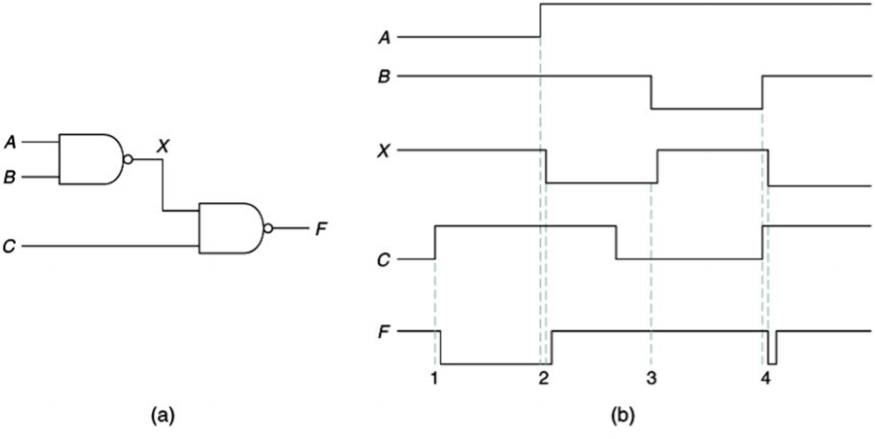
이때 각 입력과 출력에는 어쩔 수 없는 Delay가 존재하게 된다.이것을 Gate Delay라고 부른다.

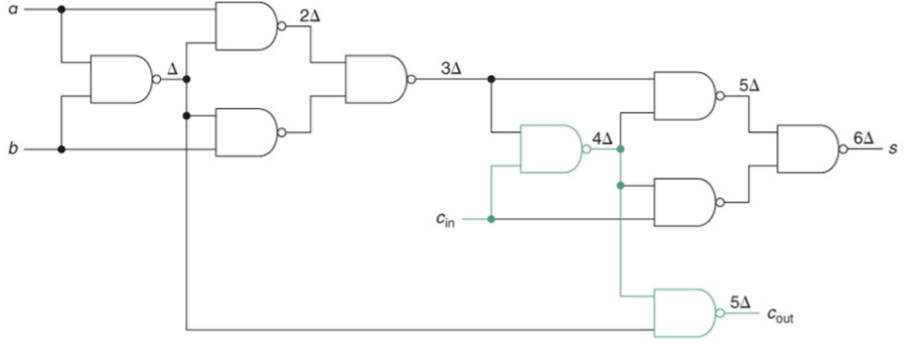
전가산기를 NAND로만 구성하면 위와 같은 그림이 나오게 된다. a와 b의 입력을 4개의 NAND만으로 XOR을 구성한 모습을 볼 수 있다. 그래서 위의 논리게이트는 자주사용하기 때문에 가급적 암기해 놓는 것이 좋다.

그렇다면 n-bit adder의 delay는 얼마일까? 이걸 만들기 위해서 ripple carry adder(병렬가감산기)을 이야기 하는데 ripple carry adder은 다음과 같은 것을 이야기 한다.

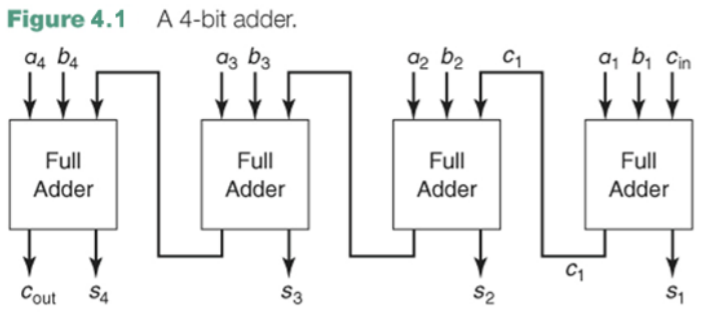
위와 같이 결과물을 다음 adder에 넣는 것을 리플-캐리 가산기라고 이야기 한다. 여기에서 delay가 발생하는 것은 계산 결과를 넘기는 과정중에 생기게 된다.

(2n+4)Δ
n bit을 넣고 걸리는 delay 이다.

왜 그런 것일까?

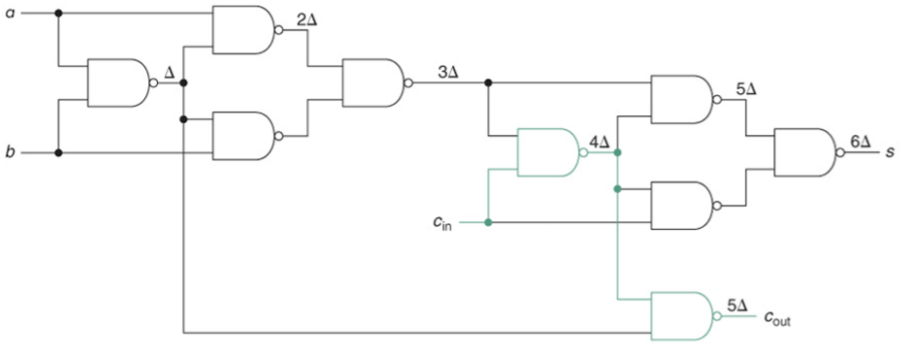
위의 그림을 봐보자 1-bit 연산기 인데 그 결과물은 6Δ가 걸리게 된다. sum을 위해서는 3Δ가 걸린다. 반면 carry를 위해서는 2Δ가 걸리게 된다. 처음의 3Δ는 c_in이 없기 전의 상황이기 때문에 어쩔 수 없이 소모하여야 하지만 그 다음부터는 이전에 받은 5Δ짜리 carry와 함께 2Δ만큼 추가 되게 된다.

여기에서 하나 알아 두어야 하는 것은 이전 가산기에서 받는 것은 carry이고 결과로 내놓는 것은 sum이다. 즉 carry와 sum사이에는 1Δ만큼의 시간 차이가 생기지만. 우리가 원하는 결과는 sum의 결과물이다. 그렇다면 2-bit는 5Δ의 캐리를 받은 다음 동일하게 3Δ만큼을 이동하는 연산기를 통과하게 될 것이다.
n==2 5Δ+3Δ = 8Δ

하지만 캐리로 이동하는 것은 5Δ의 캐리 +2Δ이기 때문에
n==3 7Δ+3Δ = 10Δ
n==4 9Δ+3Δ = 12Δ
.
.
.
n=k (1+2kΔ)+3Δ = (2k+4)Δ

의 결과가 생기게 된다.

7.1.1 감산기

1. 반감산기
   d=a⊕b
   c=a'b

2. 전감산기
   d=(a⊕b)⊕c
   c=(a⊕b)'c+a'b

가산기와의 차이점은 오로지 캐리에만 존재한다. 캐리수식 앞에 꺼에 not을 붙인 형태 => 그래서 감산기는 가산기를 그대로 적은 다음 carry의 앞 부분 boolean function에 not을 붙여두자.