7. 조합논리회로

7.1. 가산기

7.1.1. Half Adder(반가산기)

7.1.2. Full Adder(전가산기)

반가산기는 2진수 한 자리 덧셈을 하므로 아랫자리에서 발생한 캐리를 고려하지 안기 때문에 2비트 이상의 2진수 덧셈은 할 수 없다. 이 캐리를 고려하여서 만든 덧셈 회로가 전가산기이다.

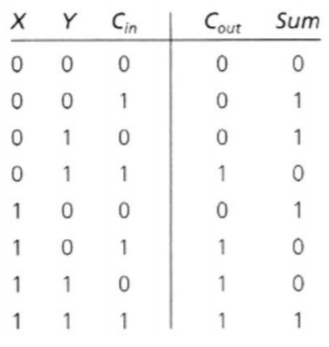
진리표는 위와 같이 입력으로 X, Y 그리고 Carry_in 결과로는 Sum과 Carry_out이 나오게 된다.

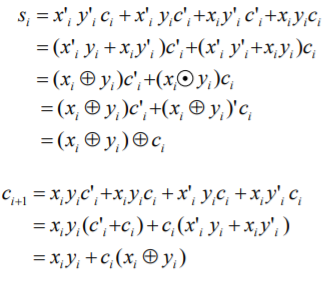
볼 대수식은 위와 같이 된다.

논리회로는
XOR 2개 / AND 2개 / OR 1개로 구성된다.

++ 교수님 팁

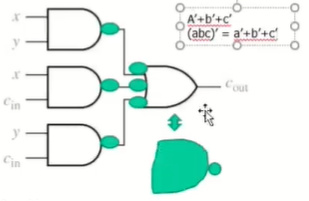
not - or 게이트는 NAND 게이트로 바꿀 수 있음.
not - and 게이트는 NOR 게이트로 바꿀 수 있음.

이때 이러한 전가산기의 주요한 문제점은 딜레이가 없어야하고
추가적으로 트랜지스터 수를 줄여서 식을 만드는 것이 중요하다.

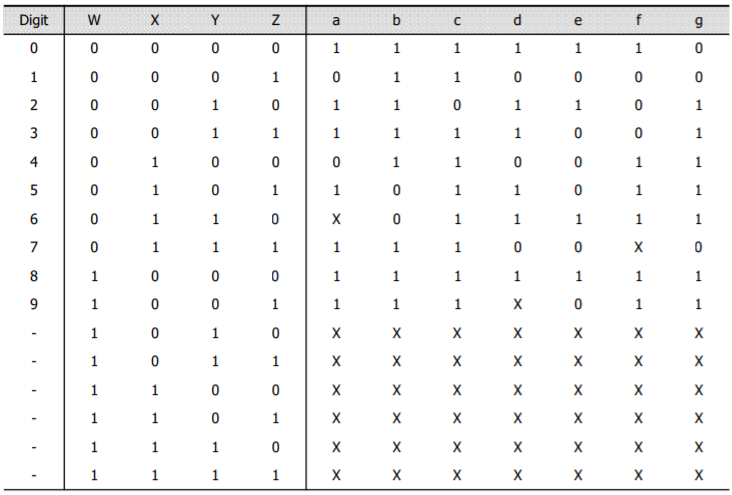
etc : A seven-segment display

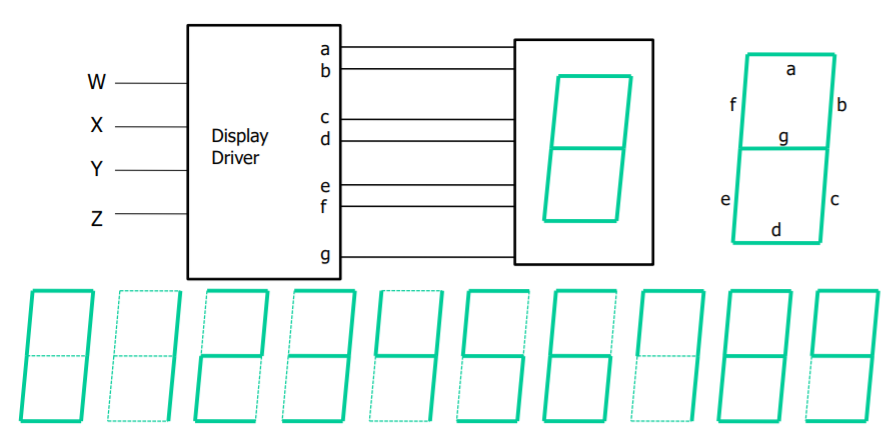
7.1.4 고속가산기

(ripple carry) 아래와 같은 병렬가산기를 리플-캐리라고 한다.

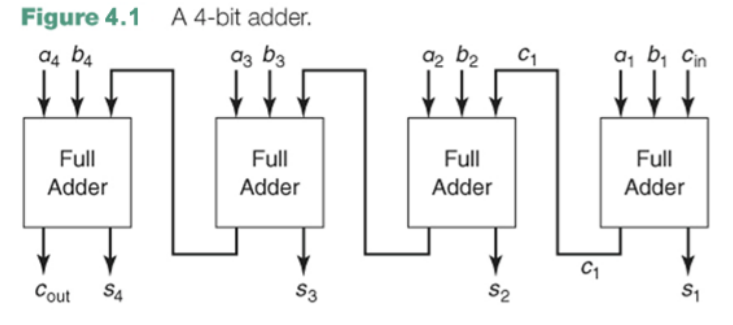
critical path delay = longest path delay => clock
cycle time을 결정

그런데 이게 리플-캐리는 속도가 빠르지 않기 때문에(딜레이가 O(n)정도 걸린다.) 이를 해결하기 위해 나온 것이 캐리예측가산기(CLA, carry-look-ahead-adder)이다. 이것은 캐리를 미리 계산하여 위로 보내는 것이다.

이제 반가산기-전가산기의 boolean function을 생각하여 보자
carry-generator g=xy
carry-propagate p=x⊕y
c_i+1 = g_i + p_i*c_i

그래서 위의 식을 쭉 늘여트려 보면 아래와 같은 결과가 나오게 된다.

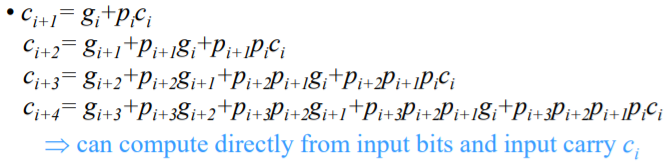
여기에서 마지막 식을 봐보자 캐리라는 값은 결국 가장 마지막에 밖에 존재하지 않는다. 즉 캐리를 제외한 나머지의 값들은 하라면 바로 만들 수 있다. 왜냐하면 컴퓨터가 시작하고 x와 y 값은 바로 제공되기 때문이다.
그렇다고 한다면 캐리값을 처음것만 구한다면 다른 가산기의 캐리값을 예측할 수 있지 않겠는가? 그렇기 때문에 이러한 방식으로 미리 캐리를 예측한다면 딜레이를 줄일 수 있을 것이다.

이제 위의 식에서 carry가 붙은 식을 제외한 부분을 따로 묶어서 공식화 해보자

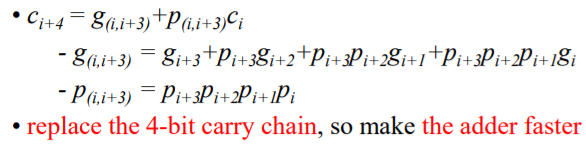
이제 이렇게 그룹화 된 부분을 generation term이라고 부른다.
대신 문제는 속도가 빨라지는 대신에 더 많은 게이트를 사용하여야 제작할 수 있다.

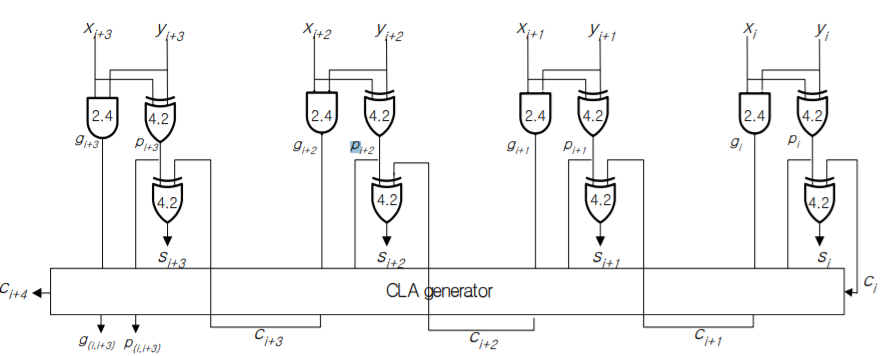
최종적으로 만드는 CLA회로는 ripple-carry에 비하여 빠를 수 밖에 없다. 이때 CLA 회로는 위의 그림의 사각형 안에 위치하고 있다.

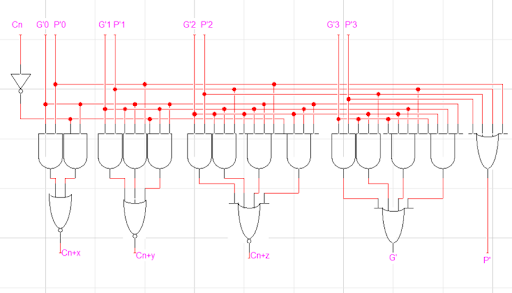
찾아보니 CLA 회로가 따로 존재한다고 한다. 위와 같이 매우 복잡하게 생기었다.

16비트짜리 CLA를 만든다 하면

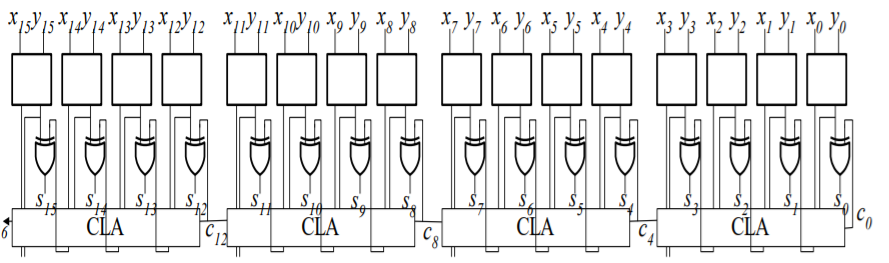
위와 같은 16비트 짜리 연산기를 만들 수 있다.

이제 이 아래에 CLA를 더 붙이면 32비트 64비트 순으로 점차 많은 비트를 계산할 수 있게 된다. 이를 2-level look-ahead adder 이라고 부른다.

그런데 이제 또 걱정인 것은 c0가 주어졌을 때 c4를 바로 만든 것처럼 c0가 주어졌을 때 2-level look-ahead adder c16 을 만들 방법은 없을까 하고 말이다.
그래서 이를 계산하는 방법에 대한 결과물은 다음과 같다.

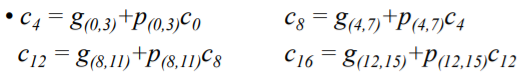
앞에 나온 수식들을 정리하면 위와 같이 생기게 될 것이다.

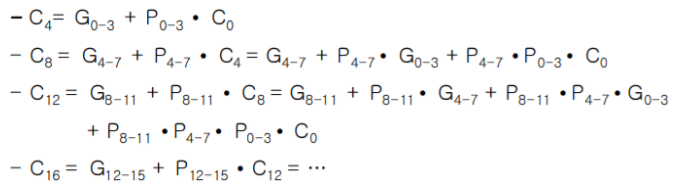
앞에서 했던것과 동일하게 모든 것을 풀어놓은 형태가 위와 같이 된다.

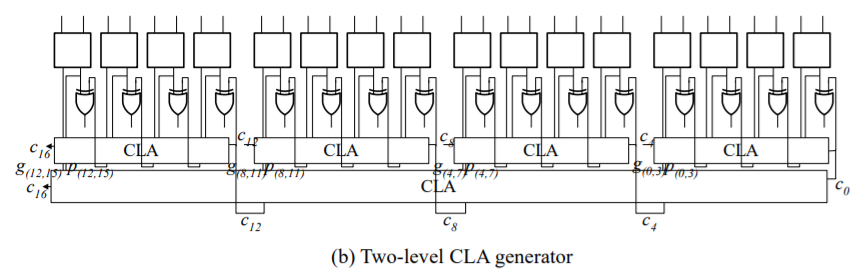
그리고 위의 수식을 이어받은 것이 위의 구조이다.

그리고 이때 마다 생기는 delay를 계산하면 위와 같은 계산들이 쭉 이어지게 된다.