Mealy machine

output이 state와 input에 동시에 dependent 한 machine을 이야기 한다.

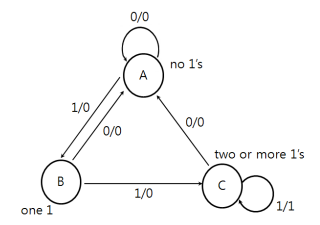
State Diagram을 보면 위와 같이 그려진다. 이때 State 위에 써 있는 숫자 0/0 에 대해서 알아보자 첫번째 0은 input이고 두번째 0은 output이다.

보면 알겠지만 이전에 나왔던 Moore Machine에 비해서 State 수가 적다. 그렇기에 Mealy Machine이 Moore Machine에 비해 State가 줄어드는 특징이 있다. 이 State를 그대로 State Table로 만들면

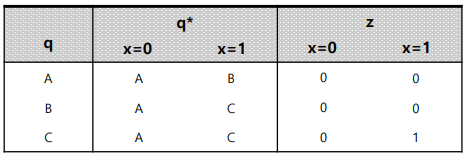
위와 같이 table이 작성되고 차이점이 Output이 input에 따라서도 변화된다는 점이다.

그래서 Mealy Machine을 사용한 예시를 보면 위와 같이 입력과 출력이 결정되는 것을 확인할 수 있다.

그런데 우리가 여기에서 본것과 같이 각 상태를 저장하기 위해서는 메모리 소자 몇개가 필요할까? 에 대한 대답이 바로 아래쪽에 나온다.

Latch

Latch는 가장 간단한 memory 성분이다.

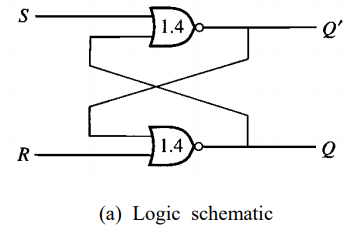
가장 간단한 SR 래치이다. 이것은 Set과 Reset이 존재하여 Set이 값을 정해주고 Reset이 값을 되돌리는 것을 이야기 한다. 그래서 Set이 1이면 Output이 1이되고 R이 1이면 Output이 0이 된다. 하지만 Set 1, Reset 1이 되면 Error가 발생한다.
위의 그래프에서 1.4의 의미는 Gate Delay를 의미한다.

특이한 점은 Input이 두개인데 하나는 외부에서 하나는 이미 출력된 결과에서 들어오게 된다. 이러한 것을 cross-coupled NOR gate라고 부른다. 이렇게 구성이 되기 때문에 이전의 출력결과를 기역하게 되는 것이다.

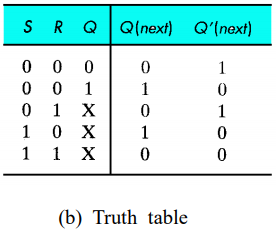
위의 표는 SR 래치가 정상작동하였을 때의 결과값을 보여준다. Q는 현재 상태를 의미하는 반면 Q'은 Q의 대조된 상태를 보여준다. 하지만 S와 R이 모두 1인 경우에는 Q와 Q'모두 0이 된다.(Error)

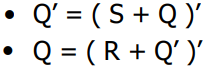
그래서 위와 같은 논리식이 구성됨을 이해할 수 있다.

SR Latch timing

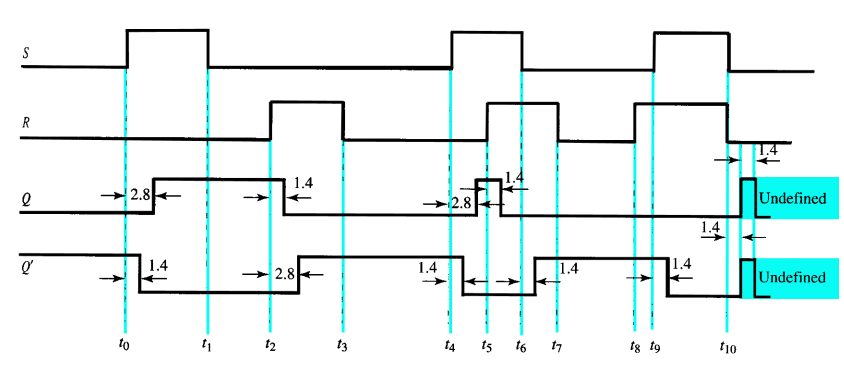
SR 래치의 입력과 출력의 지연시간을 보여준다. 위의 그림에서 보면 S가 입력되면 Q'이 더 일찍 반응하고 Q가 그 다음에 반응한다. R이 입력되면 Q가 더 일찍 반응하고 Q'이 그 다음에 반응한다. 그리고 중간에 S와 Q가 모두 입력된 순간에는 Q와 Q'모두 0이 출력되는 것을 확인할 수 있다.

그런데 마지막 Undefined 상태를 봐보자. 11이 들어와서 00의 출력을 가지고 왔다. 하지만 00으로 동시에 입력이 들어오니 11의 값이 되었다고 적혀있다. 하지만 이것은 무슨 상태인지 알 수가 없다는 것을 의미한다. 실재로 회로를 돌리어 보면 0<->1 의 값이 왔가 갔다 서로 바뀌게 된다. 그래서 SR Latch가 굉장히 unstable한 상태가 된다고 이야기 한다.\

Gated Latch

위의 문제점을 해결하기 위해서 Gate를 설치한 Latch가 만들어지게 되었다.

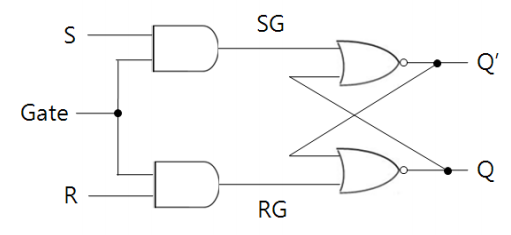
위와 같이 Gate 하나가 SR의 AND 게이트와 묶여 있는 것을 확인할 수 있다. 그렇기 때문에 Gate가 0이면 SG, RG모두 0이 되고 Latch는 상태가 변화하지 않는다. 반면 Gate가 1이면 Latch는 상태가 변화되고 값을 저장하게 된다.

Clocked SR Latch

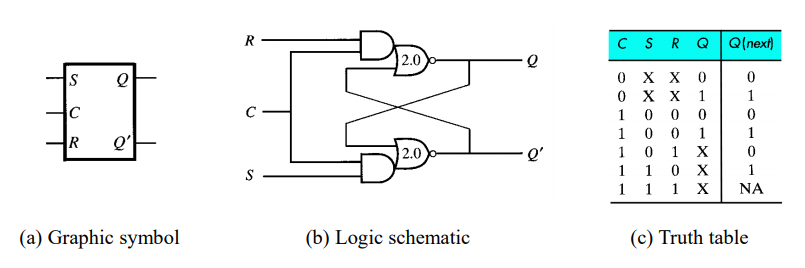
Gated Latch를 다른 말로 Clocked SR Latch라고도 부르며 회로와 진리표는 위와 같이 구성된다.

Gated D Latch

이제 위에서는 SR이 11일때 계속 문제가 생기었기에 이를 해결하고자 나온 것이 D Latch이다.

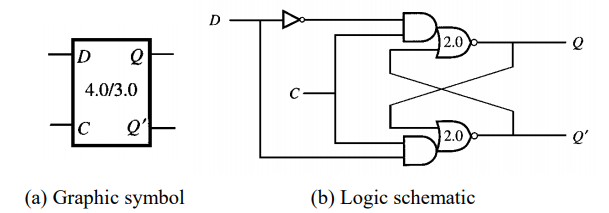
이제 이전 래치와는 다르게 D input 하나만이 들어온 다는 점이 이전 래치와는 차이점을 가지게 된다. 그리고 한쪽 회로에는 not D가 들어가기 때문에 두 게이트가 같은 값이 들어갈 경우가 없어졌다.
또한 C가 1이면 D의 입력값을 따라 출력값이 결정되지만 C가 0이면 D의 값은 유지 된다.

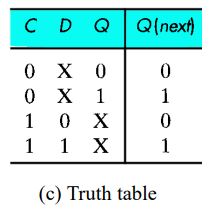
그래서 Truth table의 값을 확인해 보면 위와 같이 C가 1인 경우에 D의 값에 따라서 그 다음 출력이 결정되는 것을 확인할 수 있다.

Gated D Latch Timing

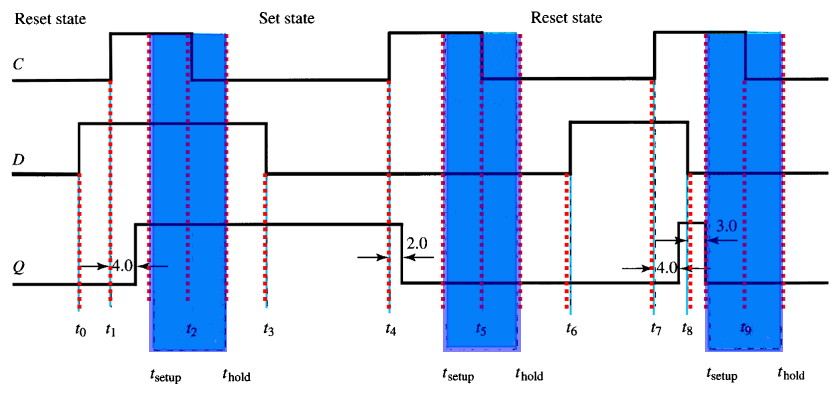
게이트 D 래치의 작동순서가 어떻게 되는지 확인해 보자. 이때 파란부분은 C가 1에서 0으로 바뀌는 시점 전후로는 D값을 같은 값으로 유지하는 것이 좋다는 의미이다.

그래서 t(setup) 과 t(hold)만큼은 input이 변하지 않는 것이 좋다는 규칙이다.

Flip Flops

하지만 래치의 문제점이 CLK이 HIGH일때 Input이 자주 바뀌면 출력값도 자주 바뀌게 된다. 이러한 문제점을 해결하기 위해 나온 것이 플립플롭이고 대다수의 컴퓨터를 만들때에도 플립플롭을 기본적인 메모리 단위로 사용하게 된다.

플립플롭은 2개의 래치를 연결하는 구조를 띄게 된다. 클럭에 따라 데이터가 저장되고 읽히는 저장 장치이다.

플립플롭이 래치와 다른점은 래치는 High 상태에서는 입력과 출력이 결정되지만 플립플롭은 HIGH 혹은 LOW로 변화하는 (rising-leading edge, falling-trailing edge) CLK 상태에서만 값이 변화하게 된다.

D Flip Flops

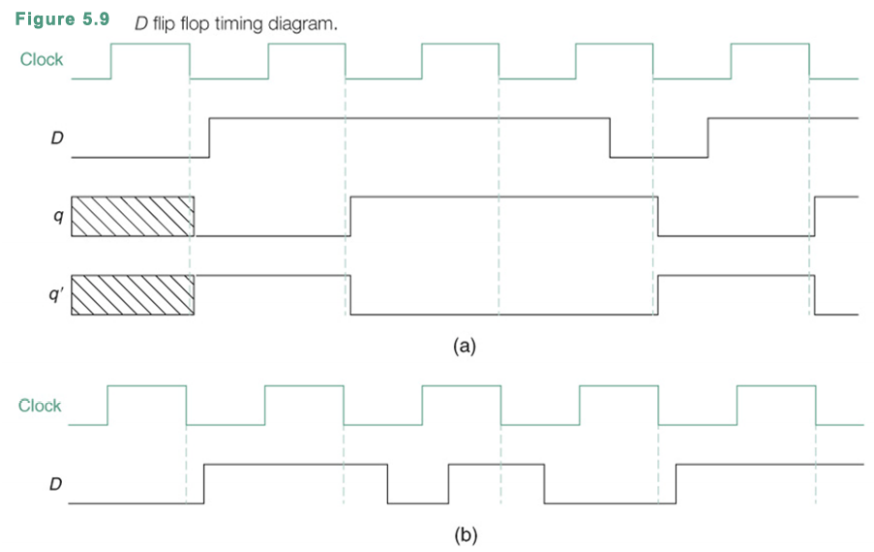
위의 그림을 보면서 D 플립플롭의 변화에 대해서 생각해 보자. 위의 그림은 falling edge에만 input이 전달된다. (a)에서 첫 falling에서 D값이 0이기에 반영된 값도 0이다. 그 다음 edge에서 1이기에 1로 반영되는 식으로 falling edge에서만 값이 변화하고 q'은 q의 inv 값이 된다.

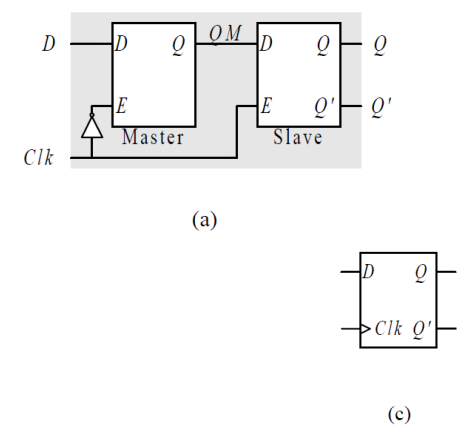
그래서 회로는 위와 같이 D 래치 두개를 연결한 master-slave 관계로 구성이 된다. CLK에 의해 Master과 Slave가 D 값을 받는 시간이 각각 정 반대인 것을 확인할 수 있다.

그리고 이때 (c) 와 같이 CLK 부분에 삼각형이 들어가게 되는데 이게 바로 플립플롭을 이야기 한다.

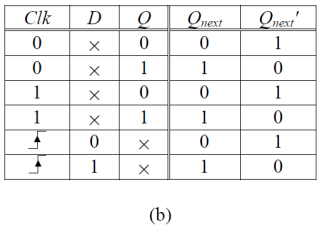
이때의 진리표를 봐보면 상승 트리거에 대해 D 값의 입력이 곧 출력으로 이어지는 것을 확인할 수 있다.

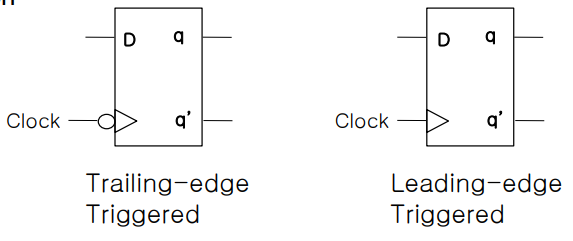
위의 플립플롭의 그림을 보면 왼쪽이 하강 엣지의 플립플롭 오른쪽이 상승 엣지의 플립플롭이다.