SR Flip Flop

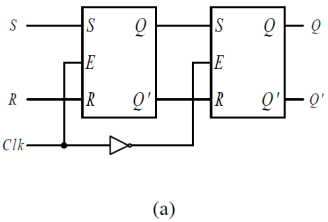
두개의 SR Latch로 만들어지는 플립플롭이다.

심볼은 위와 같이 사용한다.

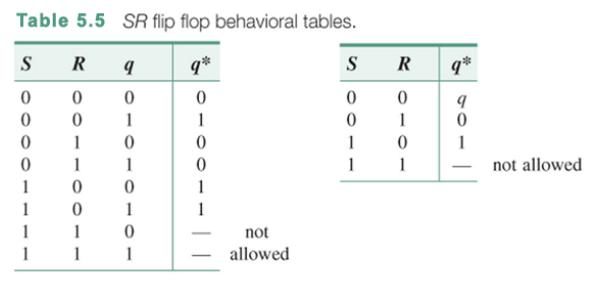
이때의 입력에 따른 변화를 보여주는 behavior table을 보면 이때에도 SR이 11이 나오는 경우는 허용되지 않는다. 이때 앞에서는 CLK를 꼭 명시해주었으나 behavior table에서 부터는 CLK를 구지 명시해 주지 않아도 모든 사람이 CLK에 따라 값이 변화한다는 것을 알고 있기 때문에 생략되었다.

그리고 오른쪽에 있는 테이블이 왼쪽의 테이블을 좀 더 간소화한 테이블이다.

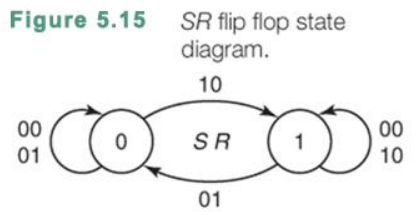
그래서 이런 테이블을 스테이트 다이어그램으로 표시하면 위와 같이 표현된다.

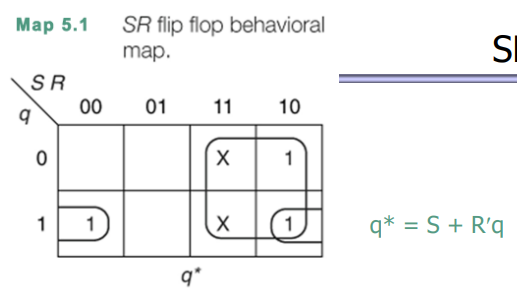
SR flip flop을 현재의 input에 따른 SR에 따른 결과를 카르노맵을 표현하면 위와 같이 표현되고 이때의 Boolean Function은 q* = S + R'q 이다.

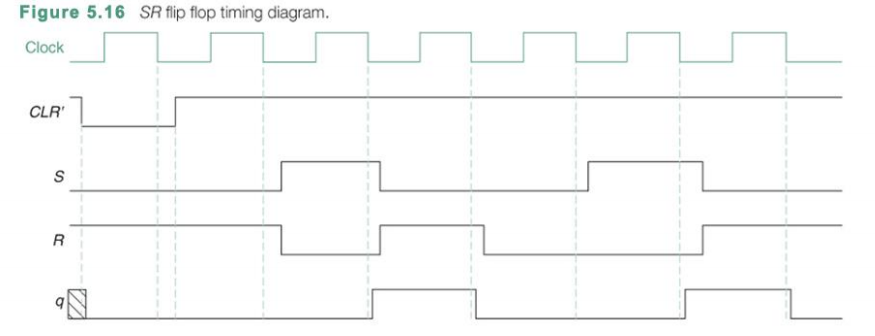
그러면 SR 플립플롭의 timing diagram을 살피어 보자 우선 보이는 것은 CLR이다. 이것은 q를 초기화 해주기 위한 값으로 사용된다. 또한 CLR이 0인 이상 S와 R의 값은 q에 영향을 미치지 않는다.

CLR로 초기화해준 다음부터는 q의 값은 S와 R에 따라 값이 변화하게 된다.

---

그런데 SR 플립플롭은 왜 D가 존재하는데도 필요한것일까? 바로 기능의 차이때문이다. SR 플립플롭이 D에 비하여 조금더 많은 기능을 가지고 있기 때문에 나중에 회로를 구성할 때 더욱 도움이 될 수 있기 때문이다.

JK Flip Flop

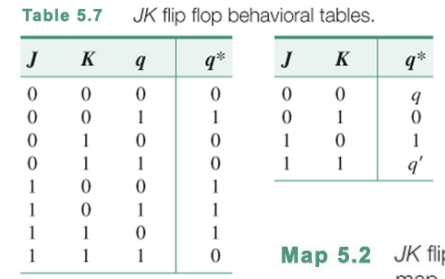
JK Flip Flop의 behavior table을 먼저 들여다 보며 이해해 보자. JK가 들어오고 현재의 state q가 존재한다. 크게 보면 SR 플리플롭과 크게 다른점이 없어 보인다. 하지만 JK 가 11일때 q* 의 값이 정해지는 것을 확인할 수 있다. 이때 JK가 11이면 q값이 toggle되어 값이 반전되게 되다.

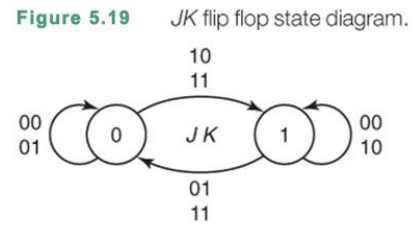
이에 대한 state diagram을 살피어 보면 위와 같이 JK에 따라 값이 결정되는 것을 확인할 수 있다.

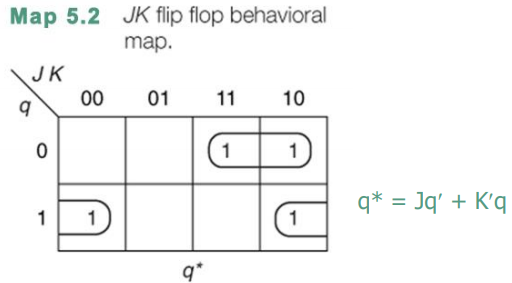
behavior map 을 보면 위와 같이 구성되어 q* = Jq' + K'q이다.

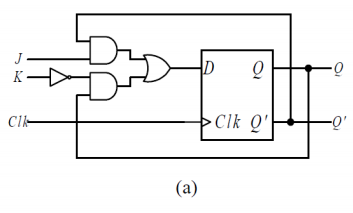
이때의 JK 플립플롭의 회로를 봐보자. 함수 식 q* = Jq' + K'q에 따라 D 플립플롭에 JK 함수식에 맞춘 논리회로가 연결되어 있는 형태이다.

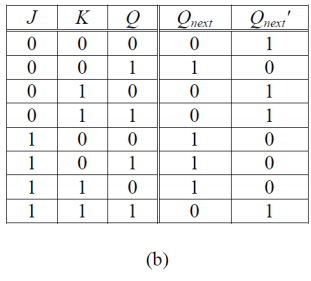
진리표는 위와 같이 구성된다.

심볼은 위와 같이 사용한다.

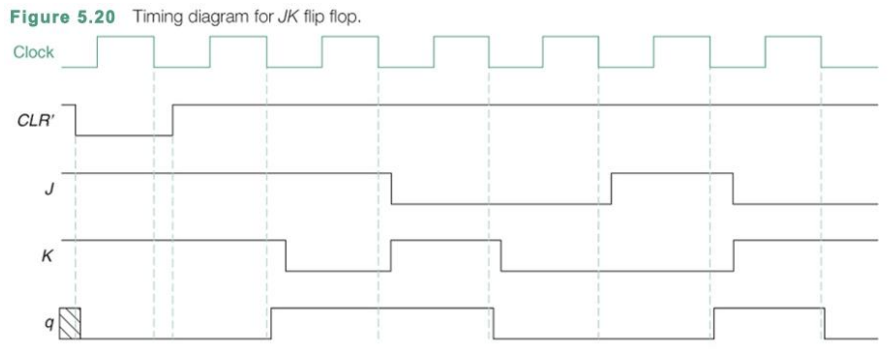
이제 Timing diagram을 봐보자 처음에는 CLR가 0으로 되어 q값을 0으로 초기화 해준다. 그 다음부터는 J와 K에 따라 set과 reset이 결정된다. 또한 JK가 11일때는 toggle이 된다는 것을 확인할 수 있다.

T Flip Flop

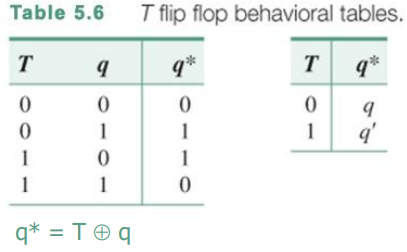
T가 0이면 유지하고 1이면 Toggle을 한다 그래서 T(Toggle) 플립플롭이라고 부른다.

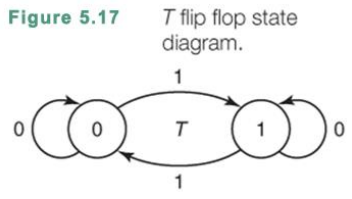
State Diagram을 확인해 보면 1일때만 값이 toggle되는 것을 확인할 수 있다.

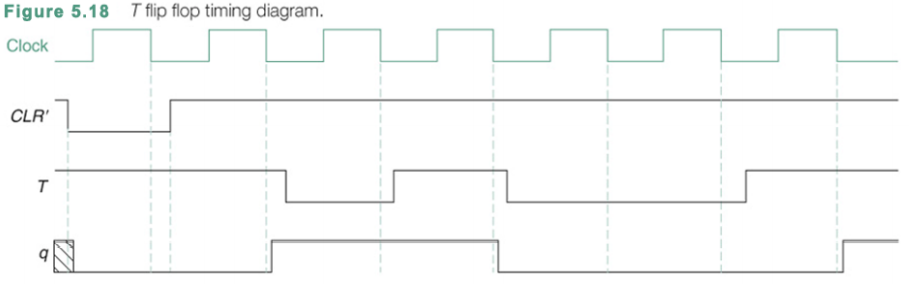
Timing Diagram을 살피어 보면 T 값에 따라 Q값이 변화하는 것을 확인할 수 있다.

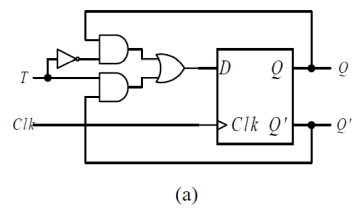
그래서 회로를 위와 같이 구성할 수 있는데 이게 사실상 q* = T xor q의 함수식을 그대로 표현한것과 다르지 않다.

심볼은 위와 같이 구성되는 것을 확인할 수 있다.

Summary of Flip Flop

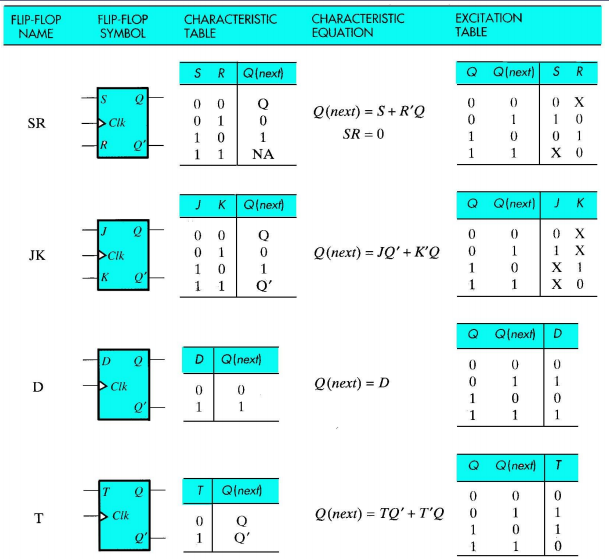
정리해주면 위와 같이 구성된다. 이때 오른쪽에 있는 표들이 재미있는 것인데 Q, Q'의 구성이 표와 같이 되기 위해서 입력이 어떻게 구성되어야 하는지를 보여준다. 이때 X는 어떤 값이든 상관없다는 의미이다.

D flip flop Moore model circuit

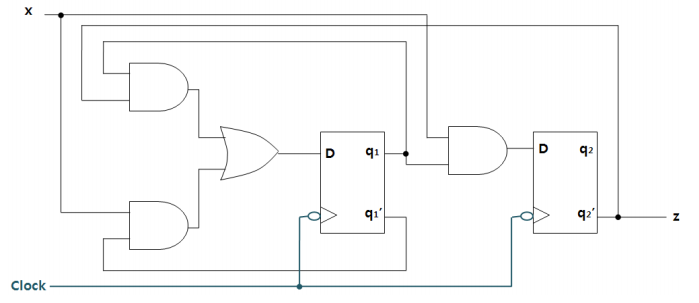
2 bit을 저장하는 회로이다. 4개의 state들을 만들 수 있다. 여기에서는 x가 직접적으로 output을 만드는데 사용되지 않았기 때문에 Moore machine이라고 부를 수 있다.

• boolean function
  D1 = q1q2’ + xq1’
  D2 = xq1
  z = q2'

q1 = D1
q2 = D2

그래서 보통 이러한 회로를 구성하기 위해서 제작 과정은 state diagram->state table->equation->circuit 이다. 하지만 우리는 reverse engineering을 활용하여서 state diagram을 제작해 보자.

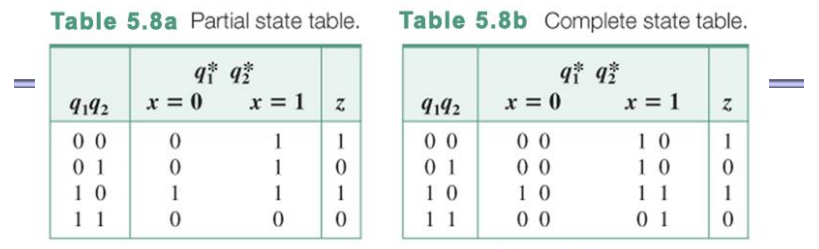
그러면 위와 같이 state table이 나오는 것을 확인할 수 있다. 왼쪽 표는 q1* 에 대해서만 테이블을 구성한 것이다.

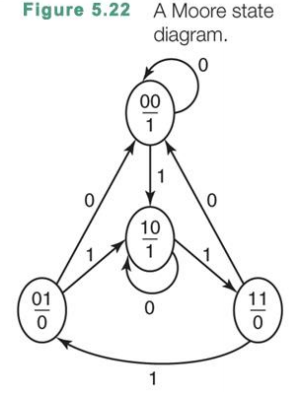
이러한 table을 diagram으로 표현해보면 위와 같이 구성되는 것을 확인할 수 있다.