디지털 회로 개론 20 (State Table)

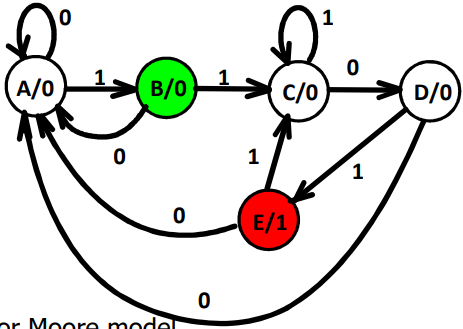
Example: Recognize 1101

이전 단원에서는 1101을 찾는 state들을 명확하게 나타내었으나 중간에 우리가 원하지 않는 패턴이 들어왔을 때 어디로 돌아가야 하는지에 대해서는 생각해 보지 않았다.

그래서 우리가 고려하지 않은 경우를 작성해 보면 위와 같이 그려지는 것을 확인할 수 있다.

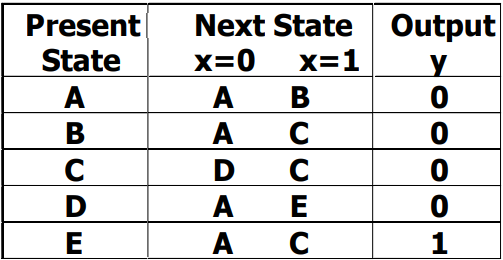
Formulation: Find State Table

그 다음 단계로 State Table을 만들어야 한다. 우리는 4개의 상태가 존재하고 하나의 입력, 하나의 출력만이 존재한다. 4개의 상태가 있는 4행을 가지게 되고 하나의 상태만이 각 상태별로 나타나야 한다.

Present State	Next State x=0   x=1	Output x=0   x=1
A	A   B	0   0
B	A   C	0   0
C	D   C	0   0
D	A   B	0   1

Implement using D Flip Flop

이제 위에서 만든 표를 가지고 D 플립플롭으로 구성을 해보자

Present State	Next State x=0   x=1	Output x=0   x=1
A(00)	A(00)   B(01)	0   0
B(01)	A(00)   C(10)	0   0
C(10)	D(11)   C(10)	0   0
D(11)	A(00)   B(01)	0   1

이전에 배운 것과 같이 D플립플롭 2개가 있어야 JK 플립플롭을 구성할 수 있다는 것을 알고 있다.

첫번째 D 플립플롭으로 들어가는 카르노맵이 존재한다고 하였을 때 이를 구성해 보면
D1

x/q1q2	00	01	11	10
0				1
1		1		1

위와 같이 카르노맵이 구성되어 D1=xQ1'Q2+Q1Q2'의 boolean Function이 생기게 된다.
D2

x/q1q2	00	01	11	10
0				1
1	1		1

이때는 위와 같이 카르노맵이 구성되어 D2=xQ1'Q2'+xQ1Q2+x'Q1Q2'

그리고 최종 아웃풋 Out = xq1q2 이다.

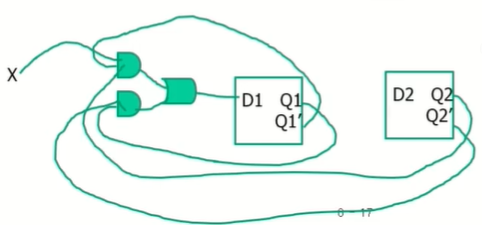
Implement using JK FFs

JK일때는 JK의 상태 4가지에 따라 어떻게 변화할지를 모두 작성해 주어야 해서 많이 복잡하다.

q	Q*	J	K
0	0	0	X
0	1	1	X
1	0	X	1
1	1	X	0

우선 위의 JK FF의 디자인 테이블을 보고 JK FF input table을 구성해 보아야 한다.

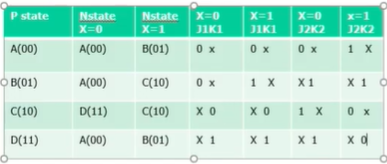
하면 최종적으로 위와 같이 생긴 표가 생기게 된다.

그래서 이렇게 만들어진 것을 J1, K1, J2, K2 에 대해서 카르노 맵을 그려 최종적인 회로를 구현할 수 있다.

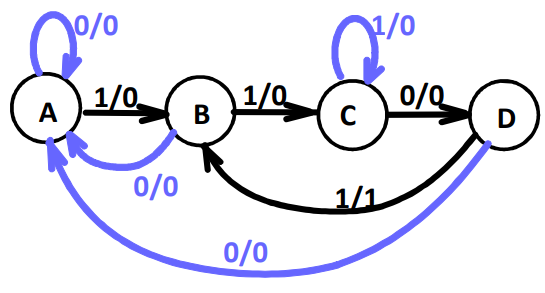
Example: Moore Model for Sequence 1101