Finite State Machines(FSM)
FSM은 State Diagram을 만들때 본 것과 같이 FSM을 이용해서 State Diagram이 만들어 진다.
– I is a set of input combinations
– O is a set of output combinations
– S is a set of states
– f is the next state function f(I, S)-Input과 Output의 function이다, and
– g is the output function f(S) [Moore model] or the output function f(I, S) [Mealy model].
Finite state machine example: design a sequence detector
X=0011011001010100
Z=0000010000010100
위와 같은 코드에서 101을 찾는다고 가정하자
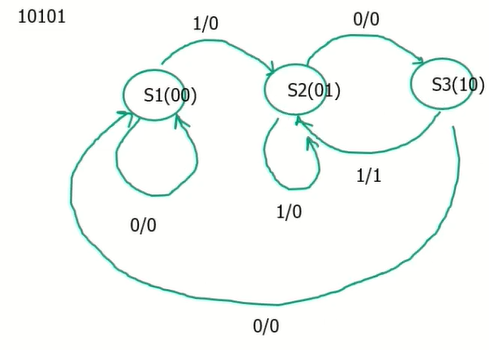
이를 위해 state를 나타내는 그림을 그리고 아래의 표를 채워보자
| x | q1 | q2 | Q1* | Q2* | z |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | x | x | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | x | x | 0 |
z=xq1q2'
Q1 = x'q2
Q2 = xq1
More Example
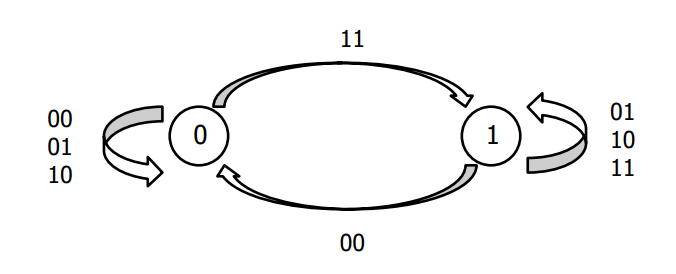
위의 것도 SR 플립플롭을 사용한 state diagram이다. 하지만 기존의 것과의 차이점이 존재한다.
1. Number of Input bits is 2
2. Output does not exist
Implementation with SR flipflops
| x | A | B | Q* | S | R |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | X |
| 0 | 0 | 1 | 0 | 0 | X |
| 0 | 1 | 0 | 0 | 0 | X |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | X | 0 |
| 1 | 1 | 0 | 1 | X | 0 |
| 1 | 1 | 1 | 1 | X | 0 |
이제 위의 표를 가지고서 카르노맵을 구현해보자
| q/AB | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | X | X | X |
S=AB
| q/AB | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 0 | X | X | 0 | X |
| 1 | 1 | 0 | 0 | 0 |
R=A'B'
Design of synchronous counter
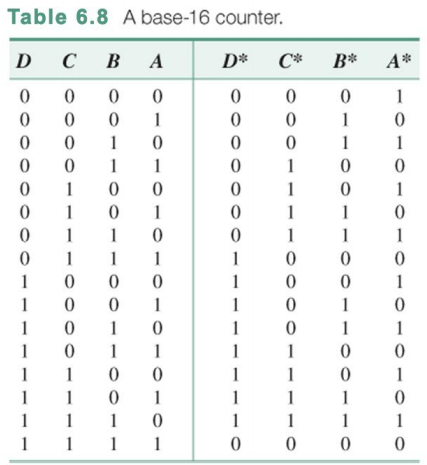
그 다음 숫자를 카운트하는 것을 카운터라고 부른다. 위에 보이는 것이 base-16 counter라고 부른다.
이 상황에서 D flip-flop을 사용하여 16개의 상태에 대한 카운터를 만들어 보자
Dd = DC’ + DB’ + DA’+ D’CBA
Dc = CB’ + CA’ + C’BA
Db = B’A + BA’
Da = A’
하면 위와 같이 카르노맵으로 나오게 된다.
하지만 이번에는 JK 플립플롭으로 이것을 디자인 해보는 과정을 거치도록 하자

