Design of synchronous counter

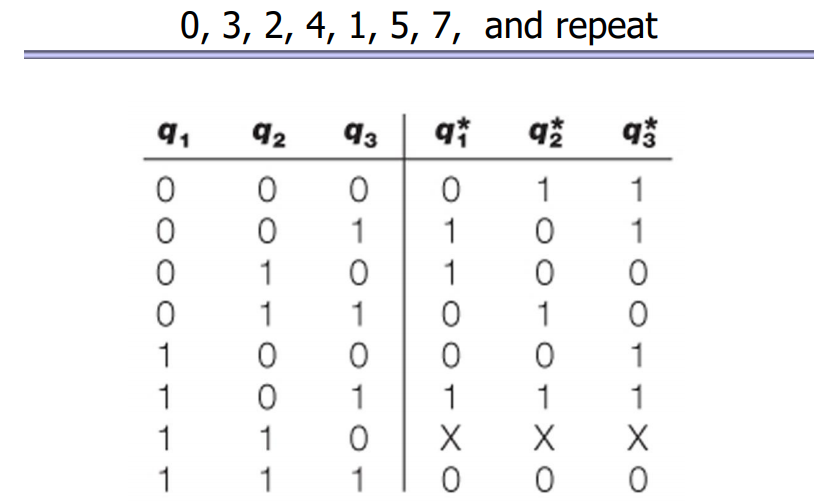
위에 보이는 것은 0->3->2->4->1->5->7->0 이 반복해서 카운트 하는 카운터이다. 그래서 6은 카운트하지 않기 때문에 만들어지면 안되는 숫자라는 의미에서 결과값이 모두 X로 처리되어 있다.

그래서 이것을 D 플립플롭으로 디자인하게 되면 D 플립플롭이 따로 필요하지 않다. 왜냐하면 결과값이 곧 입력값이 되기 때문에 이것을 카르노맵으로 바꾸어 결과를 얻어내는 것이 중요하다.

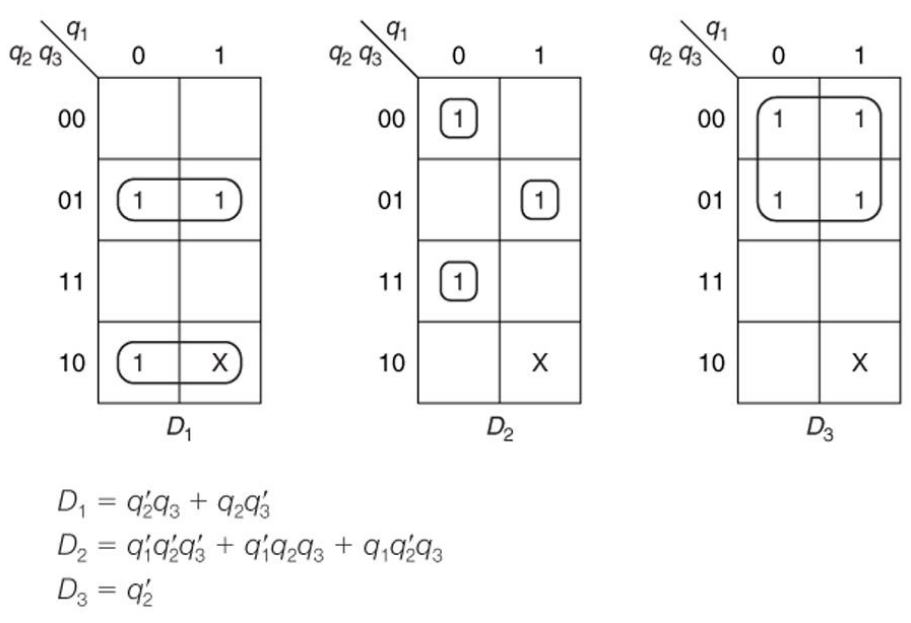
그래서 원래의 표를 카르노맵으로 묶은 결과는 위와 같이 구성되게 된다.

그렇다면 State 6에서는 어떻게 대처해야 하는 것일까? 물론 카운트상에서는 6이 나올리는 없겠으나. 만약 6으로 초기화되어 진행되었다면 어떻게 대처해야 하는 것일까?

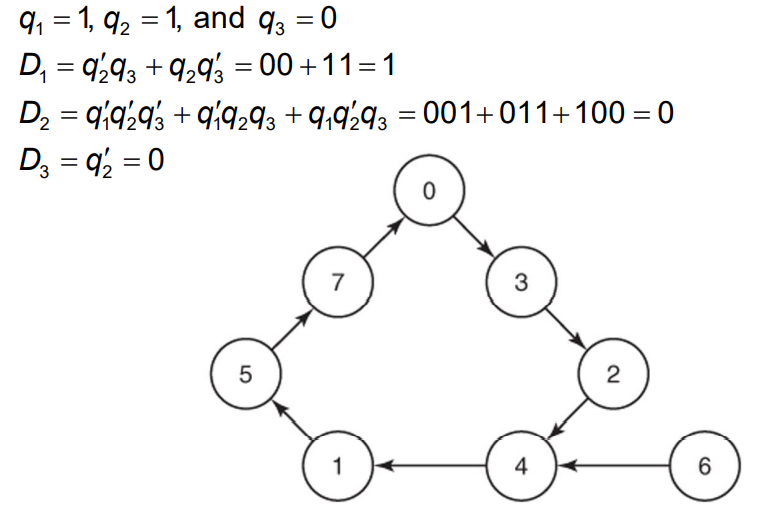
그래서 대략 이전에 짜놓은 로직을 기준으로 입력이 들어올때 그다음 상태가 어떻게 되는지 생각해 보았다. 6으로 입력이 되더라도 boolean function으로 인해 4로 들어가서 count되게 된다.

ch 7. selected topics

MOS Transistor

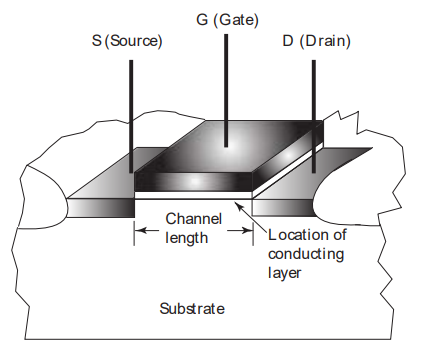
반도체 주력기술이 MOS(metal–oxide–semiconductor) Transistor이다. S와 D에 - 혹은 +를 많이 넣거나 빼고 G에 + 혹은 -를 많이 두면 원자가 이동하는 채널을 만들게 된다. 결과적으로 스위치를 만들어 게이트화시키는 것이 목적이다.

Switch Models for MOS Transistors

• NMOS
  
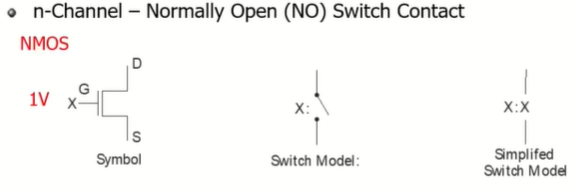
  1V를 갔다 댔을때 회로가 닫히게 되고 0V를 갔다 대면 회로가 열리게 된다.

• PMOS
  
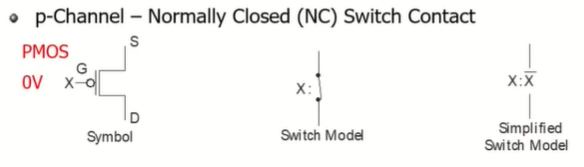
  반대로 PMOS는 0V를 갔다 댔을 때 회로가 닫히고 1V를 갔다 대면 회로가 열리게 된다.

이게 MOS 를 이용해서 Gate를 만드는 것을 CMOS logic gate(=complementary MOS)라고 부른다.

Circuits of Switch Models

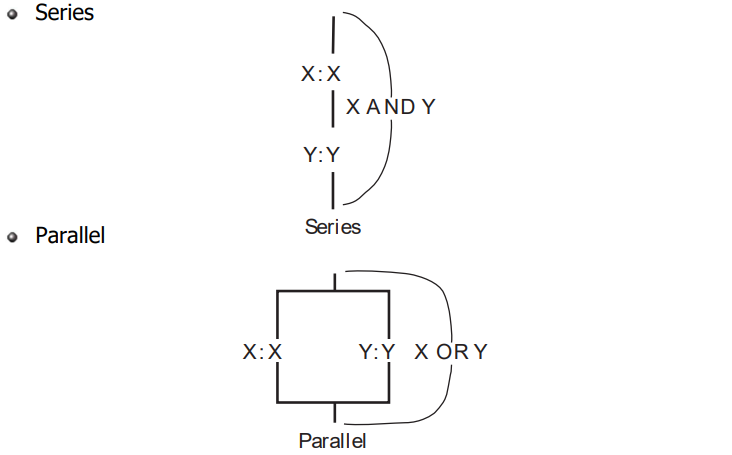
Series는 트랜지스터가 2개가 있을 때 2개가 다 Close가 되어야 모두 연결되는 것을 이야기 하고 X AND Y function이라고 부른다.

Parallel은 X또는 Y 가 연결되면 되기 때문에 X or Y Function이라고 부른다.

Fully-Complementsy CMOS Circuit

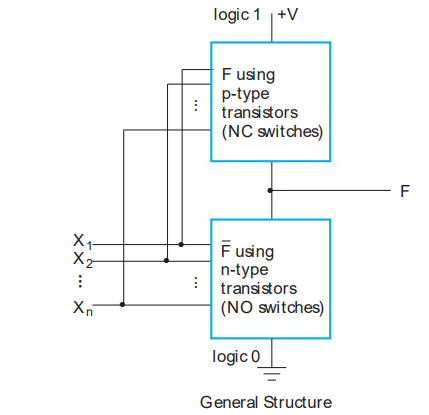
이때 우리가 트랜지스터를 설계해서 원하는 F를 만들어내는 과정을 이야기 한다.

그래서 만약에 AND 게이트를 만든다면 F가 1이 된다는 것은 위쪽 네트워크가 1V로 F와 연결되어 있다는 이야기 이고 반대로 F가 0이 된다는 것은 그라운드 네트워크가 F와 연결되어서 0이 출력된다.
그래서 상호 보완적으로 설계가 되어야 한다. 위 아래 모두 연결되면 잘못된 연결이다.

CMOS Invertor

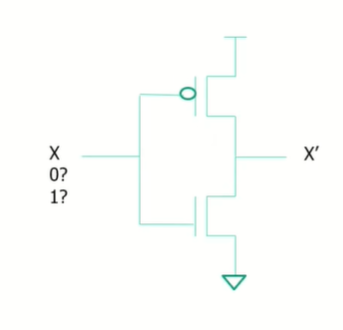
위와 같이 네트워크에 NOT이 붙어서 절때 같은 입력이 들어가는 경우가 생기지 않도록 제작해야 한다.

CMOS Circuit Design Example

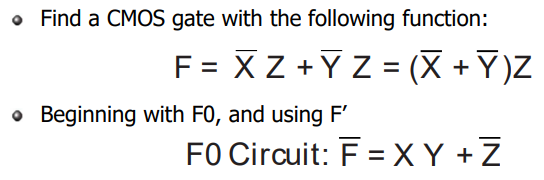
먼저 CMOS gate Function을 짠다음 이것의 not을 붙여 반대식을 구한다.

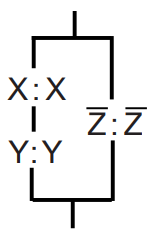
그래서 NMOS 네트워크를 생각해 보았을 때 위와 같이 구성해서 F'이 1이 되어 NMOS를 구성할 수 있다. 이것의 반대되는 네트워크를 PMOS로 구성해야 한다.

그래서 사실상 NMOS 네트워크는 아래쪽이 Ground에 연결되어 있는 형태이다.

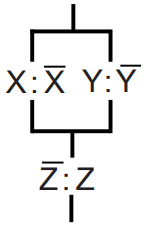
해서 PMOS로 네트워크를 구성하면 위와 같이 구성된다. PMOS는 NMOS와 다르게 위쪽 네트워크가 된어 Vdd에 연결되어 있다.

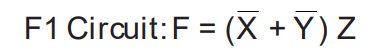
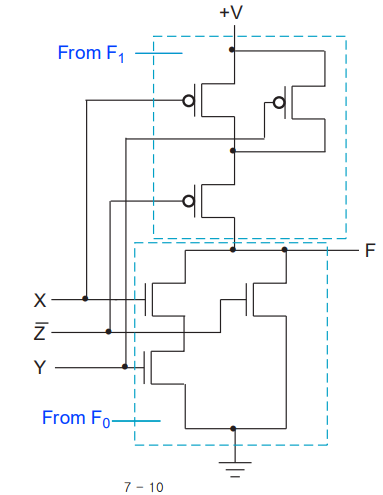
그래서 위의 식들을 최종적으로 연결하면 위와 같이 구성된다. 여기에서 중요한 것이 위쪽 네트워크는 X와 Y가 0일때 1이되고 Z가 1일때 0일때 연결이 되는 구조이다.