디지털 회로개론 05(불대수-드모르간, 최소항)

TonyHan·2020년 9월 28일

20) 디지털회로개론

목록 보기

7/24

5. 불대수

불대수는 AND, OR, NOT을 활용하여 논리식을 간소화하기 위한 수학이다. 즉, 불 대수를 이용하여 논리식을 표현할 수 있다.

5.1. 기본 논리식의 표현

진리표를 작성한다.

Boolean Funtion Evaluation

참 거짓 논리 방정식을 통과한 결과를 작성

0은 A'으로 1은 A로 표현한다.
출력은 minterm과 maxterm에 따라 다르게 표현한다.
불 대수를 실재 논리회로로 구성하기

f=x'yz'+x'yz+xy'z'+xy'z+xyz

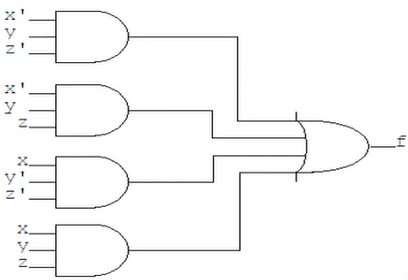
그림은 잘 못 되기는 하였지만 어찌되었든 이런식으로 논리회로를 설계하면 우리가 원하는 결과가 나올 수 있게 된다.

5.2. 불 대수 법칙-추가

드모르간의 정리(Proof of DeMorgan's Laws)

(x+y)'=x'y' / (xy)'=x'+y'

A+A' = 1 is complement를 이용한 증명
let (x+y) + (xy)' = 1
x+y+x'y' = (x+y+x')(x+y+y') [x+yz=(x+y)(x+z)]
=(1+y)(x+1) = 1·1 = 1
A·A' = 0 을 이용한 증명
let (x+y)(x'·y') = 0
x·x'·y'+y·x'y' = (0·y'+0·x') = (0+0) = 0

Complementing Functions

드모르간 법칙을 이용한 Boolean Function의 보수를 취하는 방법
1. and 와 or을 교환한다.
2. 각 숫자와 문자의 보수를 구한다.

ex>
F = x'yz'+xy'z'
F'= (x'yz'+xy'z')' = (x'yz')'(xy'z')' = (x+y'+z)(x'+y+z)

G = (a'+bc)d'+e
G' = ((a'+bc)d'+e)' = ((a'+bc)d')'e' = ((a'+bc)'+d)e' = (a(b'+c')+d)e'

H = wx'y+xy'+wxz
H' = (wx'y+xy'+wxz)' = (wx'y)'(xy')'(wxz)' = (w'+x+y')(x'+y)(w'+x'+z')

5.5 Canonical Forms(정규형) - Minterm

이제 수식 간소화 과정에 대해서 다루어 보자.

5.5.1 곱의 항과 최소항

곱의 합(SOP)은 입력 측인 1단계가 AND항(곱의 항, product term)으로 구성되고, 출력 측인 2단계는 OR(합의 항, sum term)으로 만들어진 논리식이다.

Minterm <기초>최소항
canonical form(정규형, 표준형) : 보통 functional을 기술하는데는 Simplify된 것을 사용하지만 canonical form 은 모든 literal 들이 functional describe하는데 사용되는 것을 이야기 한다. 그리고 이때 모든 변수를 사용해서 곱하기형태로 구성한 것을 minterm이라고 부른다. (변수가 하나라도 빠지면 minterm이 아니다.)

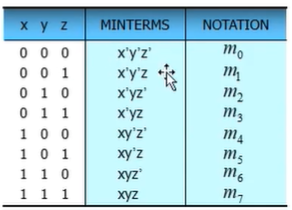
표의 수식을 보면 알겠지만 1의 입력에는 식을 그대로 사용하지만 0의 입력에는 bar을 붙여서 사용한 것을 확인할 수 있다. 그렇기에 minterm이라는 것은 항 연산의 결과가 1이 되게 하는 방정식을 이야기 한다.
Sum-of-minterms form(SOP=Sum of Product)
수식은 아래와 같이 작성한다.
F(list of variables) = Sigma(list of 1-minterm indices)

Any Boolean function can be expressed as a sum of its 1-minterms

ex>

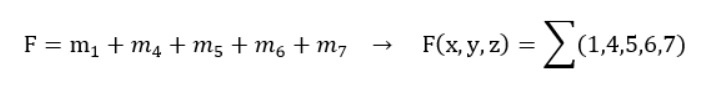
추가 공부자료
powered by : https://www.youtube.com/watch?v=GiuzhxlBwm4&ab_channel=%EB%BD%95%EA%B5%90%EC%88%98%EC%9D%98%EC%A0%84%EC%9E%90%EA%B3%B5%ED%95%99
powered by : https://m.blog.naver.com/PostView.nhn?blogId=seo0511&logNo=10125920226&proxyReferer=https:%2F%2Fwww.google.com%2F

불식 == 논리식 == 함수

여기에서 나오는 입력값(literal)은 불식을 나타내는 값이 아닌 x = 1 / x' = 0 으로 보면 이해하기 편하다.

minterm 과 maxterm은 무엇이든 보수의 관계를 가진다. 보다보면 알게 될 것이다.

위에서는 말이 많기는 했지만 그냥 우리가 보는 디지털 회로의 불식(논리식)을 구성하는 최소단위라고 생각하면 된다. 이때 진리표에서 1을 반환한 함수(불식, 논리식)에 대해서 입력값의 곱을 표현한것을 민텀 합으로 표현한 것을 맥스텀이라고 한다.

그렇기 때문에 모든 함수는 som(sum of minterm) 이라는 말은 minterm 수십개를 묶어서 함수를 만든다는 그냥 최소 함수로 최대함수를 만든다는 이야기다.

위의 사진은 대락적인 논리회로의 구성을 보여준다. 하나의 함수에는 수십개의 수식이 나올 수 있다.

이중에서 입력값들을 literal이라고 부른다.
불식을 표현하는 데에는 SOP, POS 두가지가 존재한다.

SOP(Sum of Product) : 두 개 또는 그 이상의 곱셈항들이 더해지는 형식 ex> ABC'+AB
POS(Product of Sum) : 두 개 또는 그 이상의 덧셈항들이 곱해지는 형식 ex>(A+B)(A'+C)

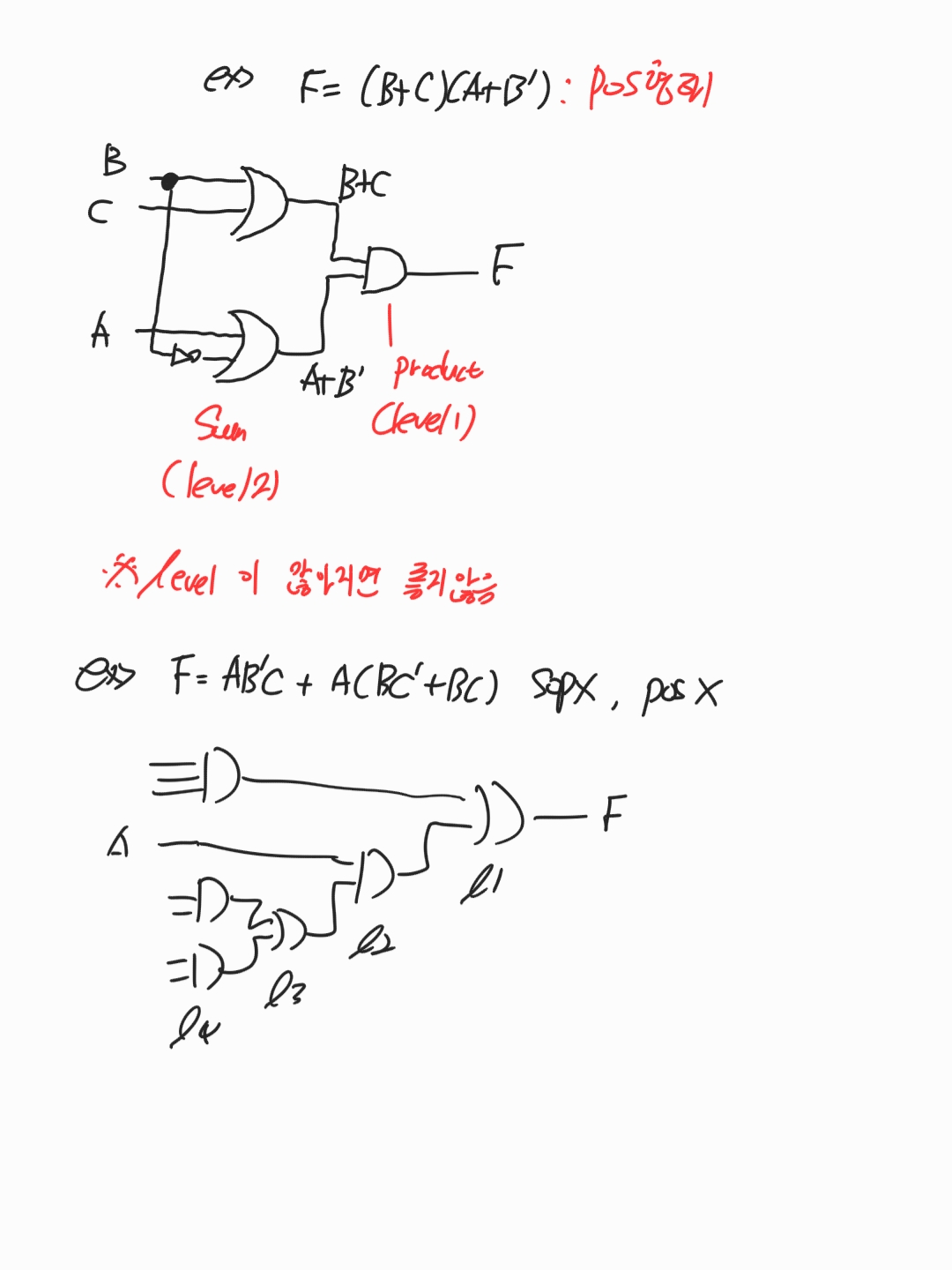
위의 표는 pos와 sop의 형태를 보여준다. 아래쪽 예시는 Product 가 마지막 Sum으로 모인것도 Sum이 Product로 모인것도 아니기 때문에 POS도 SOP도 아니다.

minterm과 maxterm은 이러한 진리표에서 1을 반환한 함수에 대해서 불 식을 곱셈 혹은 덧셈으로 표현한 것이다.

ex> minterm의 literal이 A,B라면 나올 수 있는 것은 AB, A'B, AB', A'B' 이렇게 4가지 이다. / 비슷하게 maxterm이라면 A, A', B, B' 4가지가 나올 수 있다.

minterm	maxterm

위의 사진은 실재로 minterm과 maxterm을 표현한 것이다.

이때 수식을 단순화 하기 위해 진리표의 순서대로 m_i 의 기호가 붙게 된다.
또한 드모르간 법칙에 의해 Maxterm M_j = Minterm (m_j)' 으로 볼 수 있다.

또한 minterm은 세부적으로 0-minterm과 1-minterm으로 나뉠 수 있다.

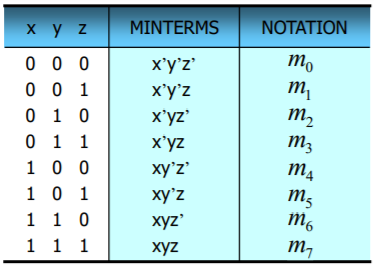
위와 같은 진리표가 존재할때

F1=x'yz+xy'z+xyz'+xyz : 1-minterms 라고 부른다. F1 식을 1로 만드는 minterm들이기 때문이다. (진리표에 표시되지 않았지만 원래 결과는 x'yz+xy'z+xyz'+xyz의 결과는 모두 1이다. - 표현만 x'이지 그냥 0의 literal 이라는 의미이다.)

F1'=x'y'z'+x'y'z+x'yz'+xy'z' : 0-minterms 라고 부른다. F1'식을 1로 만드는 minterm들 혹은 F1값을 0으로 만드는 minterm들이다. (진리표에 표시되지 않았지만 원래 결과는 x'y'z'+x'y'z+x'yz'+xy'z'의 결과는 모두 0이다.)