4.8 Change of basis

Jaehyun_onelion·2023년 3월 17일
Linear Algebra선형대수학
0

선형대수학

목록 보기
25/42

이번 포스트에서는 change of basis에 대해 알아보겠습니다.


1) Change of basis


이전 포스트에서 vector space의 basis와 vector space에 속하는 벡터들에 대해 basis 벡터의 linear combination으로 표현을 하면, 그 때의 coefficient를 coordinate vector라고 하였습니다. 이 coordinate vector는 basis가 정해지면 벡터마다 unique하게 결정이 됩니다. 또한 벡터를 coordinate vector로 변환하는 과정이 coordinate mapping이고, one-to-one, onto, linear transformation인 것을 알 수 있었습니다. 이 점을 이용하여 basis를 변화하였을 때 coordinate vector가 어떻게 변화하는지 다루어보겠습니다.

다음 예시를 살펴봅시다.


example

어떤 vector space의 basis가

B={b1,b2},   C={c1,c2}B = \{\boldsymbol{b_1}, \boldsymbol{b_2}\}, \ \ \ C = \{\boldsymbol{c_1}, \boldsymbol{c_2}\}

이고, 이 vector space에 속한 x\boldsymbol{x}가

x=3b1+b2,   x=6c1+4c2\boldsymbol{x} = 3\boldsymbol{b_1} +\boldsymbol{b_2}, \ \ \ \boldsymbol{x} =6\boldsymbol c_1 + 4\boldsymbol c_2

다음과 같이 표현된다면, x\boldsymbol{x}의 basis B,CB, C에 대한 coordinate vector는

[x]B=[31],[x]C=[64][\boldsymbol{x}]_B = \begin{bmatrix}3 \\ 1\end{bmatrix}, [\boldsymbol{x}]_C= \begin{bmatrix}6 \\ 4\end{bmatrix}

입니다.

여기서

b1=4c1+c2,    b2=−6c1+c2\boldsymbol{b_1}=4\boldsymbol{c_1} + \boldsymbol{c_2}, \ \ \ \ \boldsymbol{b_2}=-6\boldsymbol{c_1}+\boldsymbol{c_2}

라는 것을 알고 있다면, x\boldsymbol{x}를 모르더라도, BB의 coordinate vector를 이용하여 [x]C[\boldsymbol{x}]_C를 구할 수 있습니다.

x=3b1+b2=a1c1+a2c2\boldsymbol{x} = 3\boldsymbol{b_1} + \boldsymbol{b_2} = a_1\boldsymbol{c_1}+a_2\boldsymbol{c_2}

이 식을 만족하는 a1,a2a_1, a_2를 찾아야 합니다. 이 때 b1,b2\boldsymbol{b_1}, \boldsymbol{b_2} 에 c1,c2\boldsymbol{c_1}, \boldsymbol{c_2}에 대한 식을 대입하면

3b1+b2=3(4c1+c2)+(−6c1+c2)=6c1+4c23\boldsymbol{b_1} + \boldsymbol{b_2} = 3(4\boldsymbol{c_1} + \boldsymbol{c_2}) + (-6\boldsymbol{c_1} + \boldsymbol{c_2}) = 6\boldsymbol{c_1} + 4\boldsymbol{c_2}

가 됩니다. 다음 식의 coefficient를 다른 방식으로 표현하면

[x]C=[64]=[3×4+1×(−6)3×1+1×1]=[4−611][31]=[[b1]C[b2]C][x]B[\boldsymbol{x}]_C = \begin{bmatrix}6 \\ 4\end{bmatrix} = \begin{bmatrix}3\times 4 +1 \times (-6) \\ 3\times 1 + 1\times 1\end{bmatrix} = \begin{bmatrix}4 & -6\\1 & 1 \end{bmatrix}\begin{bmatrix}3 \\ 1\end{bmatrix} = \begin{bmatrix}[\boldsymbol{b_1}]_C & [\boldsymbol{b_2}]_C\end{bmatrix}[\boldsymbol{x}]_B

인 것을 알 수 있습니다. 즉, BB basis에 속한 벡터들의 CC-coordinate vector와 x\boldsymbol{x}의 BB-coordinate vector를 이용하여 x\boldsymbol{x}의 CC-coordinate vector를 구할 수 있습니다.


Theorem

Let B={b1,b2,...,bn}B = \{\boldsymbol{b_1}, \boldsymbol{b_2}, ..., \boldsymbol{b_n}\} and C={c1,c2,...,cn}C = \{\boldsymbol{c_1}, \boldsymbol{c_2}, ..., \boldsymbol{c_n}\} be bases of a vector space VV.

Then there is a unique n×nn \times n matrix PC←BP_{C\leftarrow B} such that

[x]C=PC←B[x]B[\boldsymbol{x}]_C = P_{C\leftarrow B}[\boldsymbol{x}]_B

The columns of PC←BP_{C\leftarrow B} are the CC-coordinate vectors of the vectors in the basis BB

PC←B=[[b1]C...[bn]C]P_{C\leftarrow B} = \begin{bmatrix} [\boldsymbol{b_1}]_C & ... & [\boldsymbol{b_n}]_C \end{bmatrix}

The matrix PC←BP_{C\leftarrow B} is called the change-of-coordinates matrix from BB to CC.

Multiplication by PC←BP_{C\leftarrow B} converts BB-coordinates into CC-coordinates.

BB basis의 CC-coordinate vector를 column으로 가지는 matrix PC←BP_{C\leftarrow B}를 이용하여 [x]B[\boldsymbol{x}]_B를 [x]C[\boldsymbol{x}]_C로 변환할 수 있습니다. (증명은 appendix 참고)

현재 BB가 basis이므로 BB는 linearly independent set입니다. 따라서 basis의 CC-coordinate vector 역시 linearly independent합니다. 따라서 PC←BP_{C\leftarrow B}는 linearly independent합니다. 또한, PC←BP_{C\leftarrow B}는 square matrix이므로, invertible합니다.

[x]C=PC←B[x]B[\boldsymbol{x}]_C = P_{C\leftarrow B}[\boldsymbol{x}]_B

의 양변에 PC←B−1P_{C\leftarrow B}^{-1}을 곱해주면

PC←B−1[x]C=[x]BP_{C\leftarrow B}^{-1}[\boldsymbol{x}]_C = [\boldsymbol{x}]_B

가 됩니다. 이 때, 위 식을 해석하면 x\boldsymbol{x}의 CC-coordinate vector에 PC←B−1P_{C\leftarrow B}^{-1}을 곱하게 되면 x\boldsymbol{x}의 BB-coordinate vector가 됩니다. 따라서,

PC←B−1=PB←CP_{C\leftarrow B}^{-1} = P_{B\leftarrow C}

인 것을 알 수 있습니다. 다음 상황을 시각적으로 표현하면 다음과 같습니다.

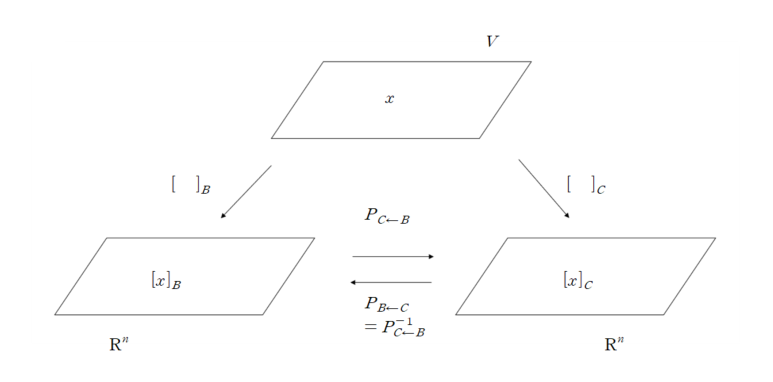
Vector space에 속하는 x\boldsymbol{x}를 BB basis의 coordinate vector로 나타낸 mapping이 왼쪽 부분 mapping, CC basis의 coordinate vector로 나타낸 mapping이 오른쪽 부분 mapping입니다. 각 coordinate vector 끼리의 변환을 쌍방향 화살표로 나타내고, 그 때 곱해주는 matrix를 PC←B,PB←CP_{C\leftarrow B}, P_{B \leftarrow C}로 나타낼 수 있습니다. 이 때, PB←C=PC←B−1P_{B\leftarrow C} = P_{C\leftarrow B}^{-1}이 됩니다.


(1) Standard basis


만약 변환시키려는 basis가 standard basis ϵ={e1,...,en}\epsilon = \{\boldsymbol{e_1}, ..., \boldsymbol{e_n}\}이라면,

[x]ϵ=x[\boldsymbol{x}]_\epsilon =\boldsymbol{x}

이므로

Pϵ←B=[[b1]ϵ[b2]ϵ...[bn]ϵ]=[b1b2...bn]=PBP_{\epsilon \leftarrow B} = \begin{bmatrix}[\boldsymbol{b_1}]_\epsilon & [\boldsymbol{b_2}]_\epsilon & ... & [\boldsymbol{b_n}]_\epsilon \end{bmatrix} = \begin{bmatrix}\boldsymbol{b_1} & \boldsymbol{b_2} & ... & \boldsymbol{b_n} \end{bmatrix} = P_B

가 되어 이전 포스트에서 다루었던 change of coordinates matrix form BB to the standard basis in Rn\mathbb R^n이 됩니다.


example

b1=[−91],  b2=[−5−1],  c1=[1−4],  c2=[3−5]\boldsymbol{b_1} = \begin{bmatrix} -9 \\ 1 \end{bmatrix}, \ \ \boldsymbol{b_2} = \begin{bmatrix} -5 \\ -1 \end{bmatrix}, \ \ \boldsymbol{c_1} = \begin{bmatrix} 1 \\ -4 \end{bmatrix}, \ \ \boldsymbol{c_2} = \begin{bmatrix} 3 \\ -5 \end{bmatrix}

이고

B={b1,b2},  C={c1,c2}B=\{\boldsymbol{b_1}, \boldsymbol{b_2}\}, \ \ C=\{\boldsymbol{c_1}, \boldsymbol{c_2}\}

가 각각 R2\mathbb R^2의 basis입니다. 이 때 PC←BP_{C\leftarrow B}와 PB←CP_{B\leftarrow C}를 구해보도록 하겠습니다.

PC←B=[[b1]C[b2]C]P_{C\leftarrow B} = \begin{bmatrix}[\boldsymbol{b_1}]_C & [\boldsymbol{b_2}]_C \end{bmatrix}

이므로,

PC[b1]C=b1 [13−4−5][b1]C=b1 [b1]C=PC−1b1=1−5+12[−5−341][−91]=17[42−35]=[6−5]P_C[\boldsymbol{b_1}]_C = \boldsymbol{b_1} \\ \ \\ \begin{bmatrix}1 & 3 \\ -4 & -5\end{bmatrix}[\boldsymbol{b_1}]_C =\boldsymbol{b_1} \\ \ \\ [\boldsymbol{b_1}]_C = P_C^{-1}\boldsymbol{b_1} = \frac{1}{-5+12}\begin{bmatrix}-5 & -3 \\ 4 & 1 \end{bmatrix}\begin{bmatrix}-9 \\ 1 \end{bmatrix} = \frac{1}{7}\begin{bmatrix}42 \\-35 \end{bmatrix} = \begin{bmatrix} 6 \\ -5 \end{bmatrix}
[b2]C=PC−1b2=1−5+12[−5−341][−5−1]=17[28−21]=[4−3][\boldsymbol{b_2}]_C = P_C^{-1}\boldsymbol{b_2} = \frac{1}{-5+12}\begin{bmatrix}-5 & -3 \\ 4 & 1 \end{bmatrix}\begin{bmatrix}-5 \\ -1 \end{bmatrix} = \frac{1}{7}\begin{bmatrix}28 \\-21 \end{bmatrix} = \begin{bmatrix} 4 \\ -3 \end{bmatrix}

따라서

PC←B=[64−5−3]P_{C\leftarrow B} =\begin{bmatrix}6 & 4 \\ -5 & -3 \end{bmatrix}

이 됩니다.

PB←C=PC←B−1P_{B\leftarrow C} = P_{C\leftarrow B}^{-1}

이므로

PB←C=12[−3−456]P_{B\leftarrow C} = \frac{1}{2}\begin{bmatrix}-3 & -4 \\ 5 & 6 \end{bmatrix}

이 됩니다.

지금까지 change of basis에 대해 알아보았습니다. 다음 포스트에서는 eigenvector, eigenvalue에 대해 알아보겠습니다. 질문이나 오류 있으면 댓글 남겨주세요! 감사합니다!


Appendix : Proof of Theorem


Theorem

Let B={b1,b2,...,bn}B = \{\boldsymbol{b_1}, \boldsymbol{b_2}, ..., \boldsymbol{b_n}\} and C={c1,c2,...,cn}C = \{\boldsymbol{c_1}, \boldsymbol{c_2}, ..., \boldsymbol{c_n}\} be bases of a vector space VV.

Then there is a unique n×nn \times n matrix PC←BP_{C\leftarrow B} such that

[x]C=PC←B[x]B[\boldsymbol{x}]_C = P_{C\leftarrow B}[\boldsymbol{x}]_B

The columns of PC←BP_{C\leftarrow B} are the CC-coordinate vectors of the vectors in the basis BB

PC←B=[[b1]C...[bn]C]P_{C\leftarrow B} = \begin{bmatrix} [\boldsymbol{b_1}]_C & ... & [\boldsymbol{b_n}]_C \end{bmatrix}

  • Proof

VV에 있는 x\boldsymbol{x}를 다음과 같이 BB basis 벡터로 표현가능합니다.

x=k1b1+⋯+knbn\boldsymbol{x} =k_1\boldsymbol{b_1} + \cdots + k_n\boldsymbol{b_n} \\

따라서

[x]B=[k1⋮kn][\boldsymbol{x}]_B = \begin{bmatrix} k_1 \\ \vdots \\ k_n\end{bmatrix}

입니다. b1,...,bn\boldsymbol{b_1}, ..., \boldsymbol{b_n}을 c1,...,cn\boldsymbol{c_1}, ..., \boldsymbol{c_n}으로 다음과 같이 표현하면

bi=di1c1+⋯+dincn,   i=1,...,n\boldsymbol{b_i} = d_{i1}\boldsymbol{c_1} + \cdots + d_{in}\boldsymbol{c_n}, \ \ \ i=1, ..., n

즉,

[bi]C=[di1⋮din][\boldsymbol{b_i}]_C = \begin{bmatrix} d_{i1} \\ \vdots \\ d_{in} \end{bmatrix}

으로 표현이 가능합니다. 이를 이용하여 x\boldsymbol{x}를 표현하면 다음과 같이 표현됩니다.

x=k1b1+⋯+knbn=k1(d11c1+⋯+d1ncn)+⋯+kn(dn1c1+⋯+dnncn)=(k1d11+k2d21+⋯+kndn1)c1+⋯+(k1d1n+k2d2n+⋯+kndnn)cn\begin{aligned} \boldsymbol{x} &=k_1\boldsymbol{b_1} + \cdots + k_n\boldsymbol{b_n} \\ &=k_1(d_{11}\boldsymbol{c_1}+\cdots+d_{1n}\boldsymbol{c_n}) + \cdots + k_n(d_{n1}\boldsymbol{c_1}+\cdots+d_{nn}\boldsymbol{c_n}) \\ &=(k_1d_{11}+k_2d_{21}+\cdots+k_nd_{n1})\boldsymbol{c_1} + \cdots + (k_1d_{1n}+k_2d_{2n}+\cdots+k_nd_{nn})\boldsymbol{c_n} \end{aligned}

임을 알 수 있습니다. 따라서

[x]C=[k1d11+⋯+kndn1⋮k1d1n+⋯+kndnn]=[d11⋯dn1⋮d1n⋯dnn][k1⋮kn]=[[b1]C⋯[bn]C][x]B\begin{aligned} \left[\boldsymbol{x}\right]_C =\begin{bmatrix}k_1d_{11}+\cdots+k_nd_{n1} \\ \vdots \\ k_1d_{1n}+\cdots+k_nd_{nn}\end{bmatrix} = \begin{bmatrix}d_{11} & \cdots & d_{n1} \\ & \vdots & \\ d_{1n} & \cdots & d_{nn} \end{bmatrix}\begin{bmatrix}k_1 \\ \vdots \\ k_n \end{bmatrix} = \begin{bmatrix}[\boldsymbol{b_1}]_C & \cdots & [\boldsymbol{b_n}]_C \end{bmatrix}[\boldsymbol{x}]_B \end{aligned}

가 성립합니다.

profile
Jaehyun_onelion
데이터 분석가 새싹
이전 포스트

4.7 Coordinate system

다음 포스트

5.1 Eigenvectors and Eigenvalues

0개의 댓글