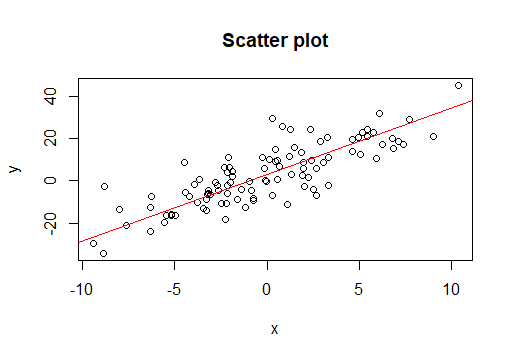
이번 포스트에서는 orthogonal projection의 응용인 linear regression(선형 회귀)에 대해서 알아보겠습니다.
1) Linear regression
(1) Linear regression
두 변수 간의 관계를 확인하고 싶을 때 데이터를 이용하여 관계를 확인할 수 있습니다. 예를 들어 다음과 같이 x , y x, y x , y ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_1, y_1), ..., (x_n, y_n) ( x 1 , y 1 ) , . . . , ( x n , y n )
우리는 x x x y y y x x x y y y x x x y y y
y = β 1 x + β 0 y=\beta_1x+\beta_0 y = β 1 x + β 0 를 표현할 수 있다면 x x x y y y x x x y y y β 1 \beta_1 β 1 x x x y y y
이를 시각적으로 표현하면 다음과 같습니다. 빨간색 직선의 기울기(β 1 \beta_1 β 1 β 0 \beta_0 β 0
(2) Notation and solution
data가 ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_1, y_1), ..., (x_n, y_n) ( x 1 , y 1 ) , . . . , ( x n , y n )
y = β 0 + β 1 x y=\beta_0 + \beta_1 x y = β 0 + β 1 x 식에서 β 0 , β 1 \beta_0, \beta_1 β 0 , β 1
y 1 = β 0 + β 1 x 1 + ϵ 1 y 2 = β 0 + β 1 x 2 + ϵ 2 ⋮ y n = β 0 + β 1 x n + ϵ n y_1 = \beta_0 + \beta_1x_1 +\epsilon_1\\ y_2 = \beta_0 + \beta_1x_2 +\epsilon_2\\ \vdots \\ y_n = \beta_0 + \beta_1x_n +\epsilon_n y 1 = β 0 + β 1 x 1 + ϵ 1 y 2 = β 0 + β 1 x 2 + ϵ 2 ⋮ y n = β 0 + β 1 x n + ϵ n 을 만족해야 합니다.(여기서 ϵ \epsilon ϵ β 0 , β 1 \beta_0, \beta_1 β 0 , β 1
Y = [ y 1 y 2 ⋮ y n ] , X = [ 1 x 1 1 x 2 ⋮ ⋮ 1 x n ] , β = [ β 0 β 1 ] , ϵ = [ ϵ 1 ϵ 2 ⋮ ϵ n ] Y=\begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_n\end{bmatrix}, \ \ X=\begin{bmatrix}1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix}, \ \ \boldsymbol \beta = \begin{bmatrix}\beta_0 \\ \beta_1\end{bmatrix}, \ \ \boldsymbol \epsilon =\begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix} Y = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 y 2 ⋮ y n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , X = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 1 1 ⋮ 1 x 1 x 2 ⋮ x n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , β = [ β 0 β 1 ] , ϵ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ 1 ϵ 2 ⋮ ϵ n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ 으로 정의하면, 위 linear system은
Y = X β + ϵ Y =X\boldsymbol \beta + \boldsymbol \epsilon Y = X β + ϵ 가 됩니다. 만약 직선이 데이터를 잘 설명한다면,
Y ≈ X β Y \approx X\boldsymbol \beta Y ≈ X β 가 만족되어야 합니다. 즉 X β X\boldsymbol \beta X β Y Y Y
∥ Y − X β ∥ \|Y-X\boldsymbol{\beta}\| ∥ Y − X β ∥ 두 벡터 사이의 거리는 작아질 것입니다. 따라서, 위 데이터를 가장 잘 설명하는 직선(β \boldsymbol{\beta} β β \boldsymbol \beta β
β ^ = arg min β ∥ Y − X β ∥ \hat{\boldsymbol \beta} = \arg\min_{\boldsymbol \beta}\|Y-X\boldsymbol \beta\| β ^ = arg β min ∥ Y − X β ∥ 이전 포스트에서, 해당 least sqaures problem의 solution은 다음의 equation을 푸는 것과 같다고 배웠습니다.
( X T X ) β = X T Y (X^TX)\boldsymbol \beta = X^TY ( X T X ) β = X T Y 만약 X T X X^TX X T X
β ^ = ( X T X ) − 1 X T Y \hat{\boldsymbol{\beta}} = (X^TX)^{-1}X^TY β ^ = ( X T X ) − 1 X T Y 로 β \boldsymbol \beta β
(3) Extension : Multiple linear regression
y y y x x x
( x 11 , . . . , x 1 p , y 1 ) , ( x 21 , . . . , x 2 p , y 2 ) , . . . , ( x n 1 , . . . , x n p , y n ) (x_{11}, ..., x_{1p}, y_1), (x_{21}, ..., x_{2p}, y_2), ..., (x_{n1}, ..., x_{np}, y_n) ( x 1 1 , . . . , x 1 p , y 1 ) , ( x 2 1 , . . . , x 2 p , y 2 ) , . . . , ( x n 1 , . . . , x n p , y n ) y y y
y = β 0 + β 1 x 1 + ⋯ + β p x p y =\beta_0 +\beta_1x_1+\cdots + \beta_px_p y = β 0 + β 1 x 1 + ⋯ + β p x p 으로 가정할 수 있습니다. 이 때, 우리가 구해야 하는 것은 β 0 , . . . , β p \beta_0, ..., \beta_p β 0 , . . . , β p
해당 문제 또한 변수가 하나였을 때와 똑같은 방법을 적용할 수 있습니다. 다만 X X X β \boldsymbol \beta β
해당 데이터가 위의 식으로 표현되어야 하므로
y i = β 0 + β 1 x i 1 + ⋯ + β p x i p + ϵ i , i = 1 , . . . , n y_i = \beta_0 + \beta_1x_{i1}+\cdots + \beta_px_{ip} +\epsilon_i, \ \ i=1,...,n y i = β 0 + β 1 x i 1 + ⋯ + β p x i p + ϵ i , i = 1 , . . . , n 으로 나타낼 수 있습니다. 이를 matrix로 표현하기 위해
Y = [ y 1 y 2 ⋮ y n ] , X = [ 1 x 11 ⋯ x 1 p 1 x 21 ⋯ x 2 p ⋮ ⋮ 1 x n 1 ⋯ x n p ] , β = [ β 0 β 1 ⋮ β p ] , ϵ = [ ϵ 1 ϵ 2 ⋮ ϵ n ] Y=\begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_n\end{bmatrix}, \ \ X=\begin{bmatrix}1 & x_{11} & \cdots & x_{1p} \\ 1 & x_{21} & \cdots & x_{2p} \\ \vdots & \vdots \\ 1 & x_{n1} & \cdots & x_{np} \end{bmatrix}, \ \ \boldsymbol \beta = \begin{bmatrix}\beta_0 \\ \beta_1 \\ \vdots \\ \beta_p\end{bmatrix}, \ \ \boldsymbol \epsilon =\begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix} Y = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 y 2 ⋮ y n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , X = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 1 1 ⋮ 1 x 1 1 x 2 1 ⋮ x n 1 ⋯ ⋯ ⋯ x 1 p x 2 p x n p ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , β = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ β 0 β 1 ⋮ β p ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , ϵ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ 1 ϵ 2 ⋮ ϵ n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ 로 설정합니다. 이 경우 Y ∈ R n , β ∈ R p , ϵ ∈ R n Y\in \mathbb R^n, \ \boldsymbol{\beta}\in\mathbb R^p, \boldsymbol \epsilon\in \mathbb R^n Y ∈ R n , β ∈ R p , ϵ ∈ R n X X X n × p n \times p n × p
Y = X β + ϵ Y =X\boldsymbol \beta + \boldsymbol \epsilon Y = X β + ϵ 이 되고, 변수가 하나였을 때와 마찬가지로
∥ Y − X β ∥ \|Y-X\boldsymbol \beta\| ∥ Y − X β ∥ 를 최소화하는 β \boldsymbol{\beta} β X T X X^TX X T X
β ^ = ( X T X ) − 1 X T Y \hat{\boldsymbol \beta} = (X^TX)^{-1}X^TY β ^ = ( X T X ) − 1 X T Y 가 됩니다.
(3) Interpretation and Projection
위의 식을 이용하여 β ^ \hat{\boldsymbol{\beta}} β ^ Y Y Y
Y ^ = X β ^ \hat Y = X\hat{\boldsymbol{\beta}} Y ^ = X β ^ 가 됩니다. 이를 각 data별로 설명하면
y ^ i = β ^ 0 + β ^ 1 x i 1 + ⋯ + β ^ x i n , i = 1 , . . . , n \hat y_i = \hat \beta_0 + \hat \beta_1 x_{i1} + \cdots + \hat \beta x_{in}, \ \ i=1,...,n y ^ i = β ^ 0 + β ^ 1 x i 1 + ⋯ + β ^ x i n , i = 1 , . . . , n 으로 표현됩니다. 해당 식의 의미를 확인하기 위해 least-sqaures problem을 살펴봅시다.
∥ Y − X β ∥ \|Y-X\boldsymbol \beta\| ∥ Y − X β ∥ 를 최소화시키는 β \boldsymbol \beta β
를 살펴봅시다. 위 식은 X X X β \boldsymbol{\beta} β
X β ∈ C o l X X\boldsymbol \beta \in ColX X β ∈ C o l X 를 만족합니다. 따라서 위 least squares problem은 C o l X ColX C o l X Y Y Y β \boldsymbol{\beta} β orthogonal projection의 성질에 의해 해당 조건을 만족하는 β \boldsymbol \beta β X β X\boldsymbol{\beta} X β p r o j C o l X Y proj_{ColX}Y p r o j C o l X Y
Y ^ = X β ^ = X ( X T X ) − 1 X T Y \hat Y = X\hat{\boldsymbol \beta} = X(X^TX)^{-1}X^TY Y ^ = X β ^ = X ( X T X ) − 1 X T Y 는 projection of Y Y Y C o l X ColX C o l X 여기서
H X = X ( X T X ) − 1 X T H_X = X(X^TX)^{-1}X^T H X = X ( X T X ) − 1 X T 를 hat matrix 또는 projection matrix라고 합니다.
2) Weighted Least-Squares Problem
(1) Weighted Least-Squares Problem
Multiple linear regression에서의 least-squares problem
∥ Y − X β ∥ \|Y-X\boldsymbol \beta\| ∥ Y − X β ∥ 에서
∥ Y − X β ∥ 2 \|Y-X\boldsymbol \beta\|^2 ∥ Y − X β ∥ 2 을 풀어서 쓰면 다음과 같습니다.
∥ Y − X β ∥ 2 = Σ i = 1 n ( y i − ( β 0 + β 1 x i 1 + ⋯ + β p x i p ) ) 2 \|Y-X\boldsymbol \beta\|^2 = \Sigma_{i=1}^n (y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}))^2 ∥ Y − X β ∥ 2 = Σ i = 1 n ( y i − ( β 0 + β 1 x i 1 + ⋯ + β p x i p ) ) 2 여기서 각 observation마다 직선 식과 실제 y y y ∥ Y − X β ∥ 2 \|Y-X\boldsymbol \beta\|^2 ∥ Y − X β ∥ 2
Σ i = 1 n w i ( y i − ( β 0 + β 1 x i 1 + ⋯ + β p x i p ) ) 2 \Sigma_{i=1}^n w_i(y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}))^2 Σ i = 1 n w i ( y i − ( β 0 + β 1 x i 1 + ⋯ + β p x i p ) ) 2 여기서 w i w_i w i w i > 0 w_i>0 w i > 0
W = d i a g ( w 1 , . . . , w n ) W = diag(w_1, ..., w_n) W = d i a g ( w 1 , . . . , w n ) 을 정의하면 해당 식은
Σ i = 1 n w i ( y i − ( β 0 + β 1 x i 1 + ⋯ + β p x i p ) ) 2 = ( Y − X β ) T W ( Y − X β ) \Sigma_{i=1}^n w_i(y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}))^2 = (Y-X\boldsymbol \beta)^TW(Y-X\boldsymbol{\beta}) Σ i = 1 n w i ( y i − ( β 0 + β 1 x i 1 + ⋯ + β p x i p ) ) 2 = ( Y − X β ) T W ( Y − X β ) 로 표현할 수 있습니다. 여기서
W 1 2 = d i a g ( w 1 , . . . , w n ) W^{\frac{1}{2}} = diag(\sqrt{w_1}, ..., \sqrt{w_n}) W 2 1 = d i a g ( w 1 , . . . , w n ) 으로 설정하면(w i > 0 w_i>0 w i > 0
( Y − X β ) T W ( Y − X β ) = ∥ W 1 2 ( Y − X β ) ∥ 2 (Y-X\boldsymbol \beta)^TW(Y-X\boldsymbol{\beta}) = \|W^{\frac{1}{2}}(Y-X\boldsymbol{\beta})\|^2 ( Y − X β ) T W ( Y − X β ) = ∥ W 2 1 ( Y − X β ) ∥ 2 이 됩니다. 다음과 같이
∥ W 1 2 ( Y − X β ) ∥ 2 \|W^{\frac{1}{2}}(Y-X\boldsymbol{\beta})\|^2 ∥ W 2 1 ( Y − X β ) ∥ 2 를 최소화시키는 β \boldsymbol \beta β Weighted-Least-Squares Problem 이라고 합니다.
(2) Solving weighted-least-squares problem
Weighted-least-squares problem을 풀기 위해서 R n \mathbb R^n R n
⟨ x , y ⟩ = x T W y \langle \boldsymbol{x}, \boldsymbol{y} \rangle = \boldsymbol{x}^TW\boldsymbol{y} ⟨ x , y ⟩ = x T W y 해당 연산은 inner product 성질을 만족합니다. (증명은 appendix 참고) 따라서 해당 inner product에 대해서 두 벡터 사이의 distance는
∥ x − y ∥ W 2 = ( x − y ) T W ( x − y ) \|\boldsymbol{x}-\boldsymbol{y}\|_W^2 = (\boldsymbol{x}-\boldsymbol{y})^TW(\boldsymbol{x}-\boldsymbol{y}) ∥ x − y ∥ W 2 = ( x − y ) T W ( x − y ) 가 됩니다. 따라서 weighted-least-squares problem에서의 식은
( Y − X β ) T W ( Y − X β ) = ⟨ ( Y − X β ) , ( Y − X β ) ⟩ = ∥ Y − X β ∥ W 2 (Y-X\boldsymbol \beta)^TW(Y-X\boldsymbol{\beta}) = \langle(Y-X\boldsymbol\beta), (Y-X\boldsymbol \beta) \rangle = \|Y-X\boldsymbol{\beta}\|_W^2 ( Y − X β ) T W ( Y − X β ) = ⟨ ( Y − X β ) , ( Y − X β ) ⟩ = ∥ Y − X β ∥ W 2 다음과 같이 표현할 수 있습니다. 즉, W W W
해당 문제의 solution을 β ^ \hat{\boldsymbol \beta} β ^ X β ^ X\hat{\boldsymbol \beta} X β ^ Y Y Y C o l X ColX C o l X
( Y − X β ^ ) ⊥ W C o l X (Y-X\hat{\boldsymbol \beta}) \perp_W ColX ( Y − X β ^ ) ⊥ W C o l X 를 만족하고 이는 X X X Y − X β ^ Y-X\hat{\boldsymbol \beta} Y − X β ^ X = [ x 1 ⋯ x p ] X = \begin{bmatrix}\boldsymbol{x_1} & \cdots & \boldsymbol{x_p} \end{bmatrix} X = [ x 1 ⋯ x p ] X X X
( Y − X β ^ ) ⊥ W x j f o r j = 1 , . . . , p (Y-X\hat{\boldsymbol \beta}) \perp_W \boldsymbol{x_j} \ \ for \ \ j =1,...,p ( Y − X β ^ ) ⊥ W x j f o r j = 1 , . . . , p 이므로
x j T W ( Y − X β ^ ) = 0 \boldsymbol{x_j}^TW(Y-X\hat{\boldsymbol \beta})=0 x j T W ( Y − X β ^ ) = 0 을 만족하므로
X T W ( Y − X β ^ ) = 0 X^TW(Y-X\hat{\boldsymbol \beta}) = 0 X T W ( Y − X β ^ ) = 0 을 만족합니다. 따라서
X T W X β ^ = X T W Y X^TWX\hat{\boldsymbol \beta} = X^TWY X T W X β ^ = X T W Y 를 만족합니다. 여기서 만약 X T W X X^TWX X T W X
β ^ = ( X T W X ) − 1 X T W Y \hat{\boldsymbol \beta} = (X^TWX)^{-1}X^TWY β ^ = ( X T W X ) − 1 X T W Y 가 됩니다.
지금까지 orthogonal projection의 응용인 linear regression과 weighted least-squares problem에 대해 알아보았습니다. 다음 포스트에서는 inner product space의 응용인 fourier series에 대해 알아보겠습니다. 질문이나 오류 있으면 댓글 남겨주세요! 감사합니다!
Appendix : Weighted-Least-Squares
Property
For x , y ∈ R n \boldsymbol x, \boldsymbol y \in \mathbb R^n x , y ∈ R n ⟨ x , y ⟩ W \langle\boldsymbol{x}, \boldsymbol{y} \rangle_W ⟨ x , y ⟩ W
⟨ x , y ⟩ W = x T W y \langle\boldsymbol{x}, \boldsymbol{y} \rangle_W = \boldsymbol{x}^TW\boldsymbol{y} ⟨ x , y ⟩ W = x T W y where
W = d i a g ( w 1 , . . . , w n ) . w i > 0 f o r i = 1 , . . . , n W=diag(w_1, ..., w_n). \ \ w_i>0 \ \ for \ \ i=1,...,n W = d i a g ( w 1 , . . . , w n ) . w i > 0 f o r i = 1 , . . . , n Then this operation satisfies inner product conditions.
해당 연산이 inner product임을 밝히기 위해서는 4가지 조건을 밝혀야 합니다.
⟨ x , y ⟩ W = ⟨ y , x ⟩ W \langle\boldsymbol{x}, \boldsymbol{y} \rangle_W =\langle\boldsymbol{y}, \boldsymbol{x} \rangle_W ⟨ x , y ⟩ W = ⟨ y , x ⟩ W
⟨ x , y ⟩ W = x T W y = Σ i = 1 n w i x i y i = Σ i = 1 n w i y i x i = y T W x = ⟨ y , x ⟩ W \langle\boldsymbol{x}, \boldsymbol{y} \rangle_W = \boldsymbol{x}^TW\boldsymbol{y} = \Sigma_{i=1}^nw_ix_iy_i = \Sigma_{i=1}^nw_iy_ix_i=\boldsymbol{y}^TW\boldsymbol{x} = \langle\boldsymbol{y}, \boldsymbol{x} \rangle_W ⟨ x , y ⟩ W = x T W y = Σ i = 1 n w i x i y i = Σ i = 1 n w i y i x i = y T W x = ⟨ y , x ⟩ W 첫 번째 조건은 성립합니다.
⟨ x + y , z ⟩ W = ⟨ x , z ⟩ W + ⟨ y , z ⟩ W \langle\boldsymbol{x}+\boldsymbol{y}, \boldsymbol{z} \rangle_W=\langle\boldsymbol{x}, \boldsymbol{z} \rangle_W + \langle\boldsymbol{y}, \boldsymbol{z} \rangle_W ⟨ x + y , z ⟩ W = ⟨ x , z ⟩ W + ⟨ y , z ⟩ W
⟨ x y , z ⟩ W = ( x + y ) T W z = x T W z + y T W z = ⟨ x , z ⟩ W + ⟨ y , z ⟩ W \langle\boldsymbol{x_y}, \boldsymbol{z} \rangle_W = (\boldsymbol{x}+\boldsymbol{y})^TW\boldsymbol{z} =\boldsymbol x^TW\boldsymbol z + \boldsymbol y^TW\boldsymbol z = \langle\boldsymbol{x}, \boldsymbol{z} \rangle_W + \langle\boldsymbol{y}, \boldsymbol{z} \rangle_W ⟨ x y , z ⟩ W = ( x + y ) T W z = x T W z + y T W z = ⟨ x , z ⟩ W + ⟨ y , z ⟩ W 두 번째 조건 또한 성립합니다.
⟨ c x , y ⟩ W = c ⟨ x , y ⟩ W \langle c\boldsymbol{x}, \boldsymbol{y} \rangle_W=c\langle\boldsymbol{x}, \boldsymbol{y} \rangle_W ⟨ c x , y ⟩ W = c ⟨ x , y ⟩ W c c c
⟨ c x , y ⟩ W = ( c x ) T W y = c ( x ) T W y = c ⟨ x , y ⟩ W \langle c\boldsymbol{x}, \boldsymbol{y} \rangle_W = (c\boldsymbol x)^TW\boldsymbol{y} = c(\boldsymbol x)^TW\boldsymbol y =c\langle\boldsymbol{x}, \boldsymbol{y} \rangle_W ⟨ c x , y ⟩ W = ( c x ) T W y = c ( x ) T W y = c ⟨ x , y ⟩ W 세 번째 조건도 성립합니다.
⟨ x , x ⟩ W ≥ 0 \langle\boldsymbol{x}, \boldsymbol{x} \rangle_W\geq 0 ⟨ x , x ⟩ W ≥ 0 ⟨ x , x ⟩ W = 0 \langle\boldsymbol{x}, \boldsymbol{x} \rangle_W=0 ⟨ x , x ⟩ W = 0 x = 0 \boldsymbol{x}=0 x = 0
⟨ x , x ⟩ W = x T W x = Σ i = 1 n w i x i 2 ≥ 0 \langle\boldsymbol{x}, \boldsymbol{x} \rangle_W = \boldsymbol x^TW\boldsymbol x = \Sigma_{i=1}^nw_ix_i^2 \geq 0 ⟨ x , x ⟩ W = x T W x = Σ i = 1 n w i x i 2 ≥ 0 이는 w i > 0 w_i>0 w i > 0 w i > 0 w_i>0 w i > 0
⟨ x , x ⟩ W = 0 ⟺ x = 0 \langle\boldsymbol{x}, \boldsymbol{x} \rangle_W = 0 \iff \boldsymbol{x} =0 ⟨ x , x ⟩ W = 0 ⟺ x = 0 이 되어야 합니다.
따라서 inner product가 되기 위한 4가지 조건을 만족하였으므로
⟨ x , y ⟩ W = x T W y \langle\boldsymbol{x}, \boldsymbol{y} \rangle_W = \boldsymbol{x}^TW\boldsymbol{y} ⟨ x , y ⟩ W = x T W y 는 inner product가 됩니다.