6.8 Application : Fourier Series

Jaehyun_onelion·2023년 3월 17일

Linear Algebra 선형대수학

선형대수학

목록 보기

37/42

이번 포스트에서는 Fourier Series에 대해 알아보겠습니다.

1) Fourier Series

(1) Set of continuous functions

다음과 같은 집합 $S$ 를 생각해봅시다.

S = \{f \mid f : [0, 2\pi] \rightarrow \mathbb R, \ f : \ continuous\}

Domain이 $[0, 2\pi]$ 이고 공역이 실수인 연속 함수들의 집합 $S$ 는 vector space가 됩니다. 이는, 함수에서의 zero vector 역할을 하는 상수함수 $y=0$ 은 연속함수이므로 다음 집합에 포함되고, 연속함수의 합과 scalar multiple 역시 연속함수이기 때문입니다. 즉, $S$ 는 vector space가 되고 이를

S = C[0, 2\pi]

로 표현할 수 있습니다.

(2) Fourier approximation

$C[0, 2\pi]$ 에서, inner product를 다음과 같이 정의해봅시다.

\langle f, g \rangle = \int_0^{2\pi}f(t)g(t)dt

다음 연산은 inner product가 되기 위한 조건을 만족합니다. 이는

$\langle f, g \rangle = \langle g, f \rangle$
$\langle f, g+h \rangle = \int_0^{2\pi}f(t)\{g(t)+h(t)\}dt = \langle f, g \rangle + \langle f, h \rangle$
$\langle cf, g \rangle = \int_0^{2\pi}cf(t)g(t)dt = c\int_0^{2\pi}f(t)g(t)dt = c\langle f, g \rangle$
$\langle f, f \rangle =\int_0^{2\pi}\{f(t)\}^2dt \geq 0, \ \ \langle f, f \rangle = 0$ if and only if $f=0$

다음 네 조건을 모두 만족하기 때문입니다. 즉, 다음의 inner product를 이용한 inner product space $C[0, 2\pi]$ 를 얻을 수 있습니다.

Inner product space $C[0, 2\pi]$ 에서 basis가 다음과 같은 subspace $W$ 를 생각해봅시다.

\{1, \cos t, \cos2t, ..., \cos nt, \sin t, \sin 2t, ..., \sin nt\} \\ \ \\ W = Span\{1, \cos t, \cos2t, ..., \cos nt, \sin t, \sin 2t, ..., \sin nt\}

다음 basis는 orthogonal한 것을 알 수 있습니다. (appendix 참고)

$C[0, 2\pi]$ 에 속하는 모든 벡터(또는 함수)는 $W$ 에 속한 벡터로 근사할 수 있습니다. projection을 이용해서 말이죠.

f \in C[0, 2\pi] \\ \ \\ \begin{aligned} Proj_W(f) = &a_0+a_1\cos t + a_2\cos 2t + \cdots + a_n \cos nt \\ &+ b_1 \sin t + b_2 \sin 2t + \cdots + b_n \sin nt\end{aligned}

여기서 $a_k, b_k$ 는 orthogonal projection 개념을 이용하여 구할 수 있습니다.

a_k = \frac{\langle\cos kt, f \rangle}{\langle \cos kt, \cos kt \rangle}, \ \ \ b_k = \frac{\langle \sin kt, f \rangle}{\langle \sin kt, \sin kt\rangle}, \ \ k=1, ..., n

이 때, $\langle \cos kt, \cos kt \rangle = \langle \sin kt, \sin kt \rangle = \pi$ 인 것을 이용하면

a_k = \frac{1}{\pi}\int_0^{2\pi}f(t)\cos kt dt , \ \ \ b_k = \frac{1}{\pi}\int_0^{2\pi}f(t) \sin kt dt, \ \ k=1, ..., n

임을 알 수 있습니다. 또한 $a_0$ 는

a_0 = \frac{\langle 1, f \rangle}{\langle1, 1 \rangle}, \ \ \langle1, 1 \rangle = \int_0^{2\pi}1dt = 2\pi, \\ \ \\ \langle1, f \rangle = \int_0^{2\pi}f(t)dt,\ \ a_0 = \frac{1}{2\pi}\int_0^{2\pi} f(t)dt

인 것을 알 수 있습니다. Notation 편의를 위해 $a_0 = \frac{1}{\pi}\int_0^{2\pi}f(t)dt$ 로 설정하면

Proj_W(f) = \frac{a_0}{2}+a_1\cos t + \cdots + a_n \cos nt + b_1 \sin t + \cdots + b_n \sin nt

와 같이 근사할 수 있습니다. 다음의 근사를 nth-order Fourier approximation to $f$ on $[0, 2\pi]$ 라고 합니다. 또한 $a_k, b_k$ 를 $f$ 의 Fourier coefficient라고 합니다.

example

f(t) =t

의 nth order Fourier approximation을 구해봅시다.

\frac{a_0}{2} = \frac{1}{2\pi}\int_0^{2\pi}tdt = \frac{1}{2\pi}\left[\frac{1}{2}t^2\right]^{2\pi}_0 = \pi

와

a_k = \frac{1}{\pi}\int_0^{2\pi} t\cos kt dt = \frac{1}{\pi}\left[\frac{1}{k}t\sin kt + \frac{1}{k^2}\cos kt\right]^{2\pi}_0 = 0 \\ \ \\ b_k = \frac{1}{\pi}\int_0^{2\pi}t\sin kt dt = \frac{1}{\pi}\left[-\frac{1}{k}t\cos kt + \frac{1}{k^2}\sin kt\right]^{2\pi}_0 = -\frac{2}{k}

을 통해

f(t) = \frac{\pi}{2} -2\sin t -\sin 2t - \frac{2}{3}\sin 3t - \cdots - \frac{2}{n}\sin nt

을 얻을 수 있습니다. 다음 식을 이용하여 3rd, 6th order Fourier approximation을 한 결과 그래프는 다음과 같습니다.

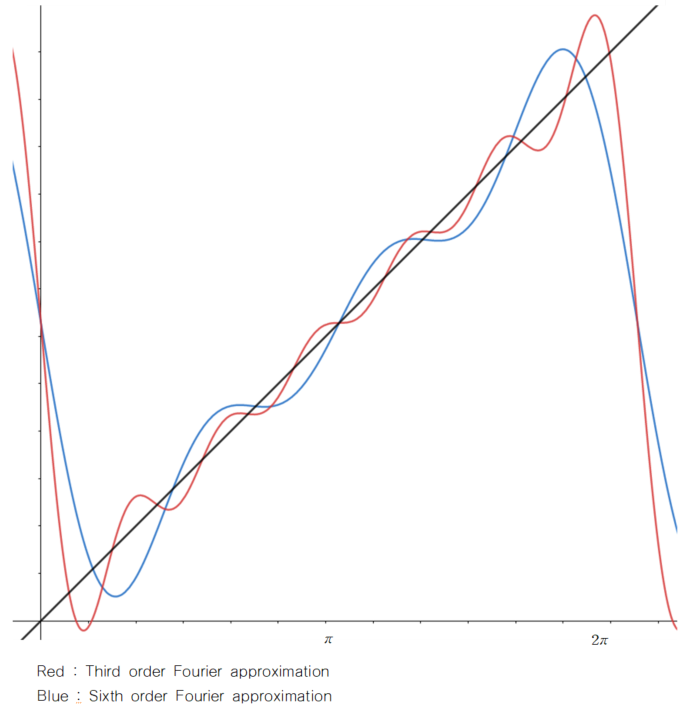
검은 직선 $f(t) =t$ 에 대한 3rd, 6th order Fourier approximation 결과를 살펴보면 order가 클수록 approximation을 잘하는 것을 알 수 있습니다. 따라서, Fourier approximation에서 n을 무한대로 보내는, 급수형태로 표현한다면 매우 정확하게 $f$ 를 근사할 수 있을 것입니다.

(3) Fourier Series

Fourier approximation에서 order가 증가할수록, 주어진 함수를 더욱 더 잘 근사할 수 있습니다. 따라서 Fourier approximation에서 order를 무한으로 늘리면 다음과 같이 무한 급수 형태로 식을 작성할 수 있습니다.

f(t) = \frac{a_0}{2} + \sum_{m=1}^\infty(a_m\cos mt + b_m \sin mt)

$f(t)$ 를 다음의 series로 표현하는 방법을 Fourier series for $f$ on $[0, 2\pi]$ 라고 합니다.

지금까지 Fourier Series에 대해 알아보았습니다. 다음 포스트에서는 symmetric matrix와 spectral decomposition에 대해 알아보겠습니다. 질문이나 오류 있으면 댓글 남겨주세요! 감사합니다!

Appendix : Proof of property

Property

Let $W$ be a subspace of the inner product space $C[0, 2\pi]$ . The basis of $W$

\{1, \cos t, \cos2t, ..., \cos nt, \sin t, \sin 2t, ..., \sin nt\}

is orthogonal basis for $W$

Proof

$\cos mt, \cos nt$ case ( $m\neq n$ )

\begin{aligned} \langle \cos mt, \cos nt \rangle &= \int_0^{2\pi} \cos mt \cos nt dt = \int_0^{2\pi}\frac{1}{2}(\cos(m+n)t + \cos(m-n)t) dt \\ &= \frac{1}{2}\left[\frac{1}{m+n}\sin (m+n)t +\frac{1}{m-n}\sin(m-n)t\right]^{2\pi}_0 \\ &=0 \end{aligned}

$\cos mt, \sin nt$ case ( $m\neq n$ )

\begin{aligned} \langle \cos mt, \sin nt \rangle &= \int_0^{2\pi} \cos mt \sin nt dt = \int_0^{2\pi} \frac{1}{2}(\sin (m+n)t -\sin(m-n)t)dt \\ &= -\frac{1}{2}\left[\frac{1}{m+n}\cos (m+n)t -\frac{1}{m-n}\cos(m-n)t\right]^{2\pi}_0 \\ &=0 \end{aligned}

$\sin mt, \sin nt$ case ( $m\neq n$ )

\begin{aligned} \langle \sin mt, \sin nt \rangle &= \int_0^{2\pi} \sin mt \sin nt dt = \int_0^{2\pi} -\frac{1}{2}(\cos (m+n)t -\cos(m-n)t)dt \\ &= -\frac{1}{2}\left[\frac{1}{m+n}\sin (m+n)t -\frac{1}{m-n}\sin(m-n)t\right]^{2\pi}_0 \\ &=0 \end{aligned}

$\cos mt, \sin mt$ case

\begin{aligned} \langle \cos mt, \sin mt \rangle &= \int_0^{2\pi} \cos mt \sin mt dt = \int_0^{2\pi} \frac{1}{2}\sin 2mt dt \\ &= \left[-\frac{1}{4m}\cos 2mt\right]^{2\pi}_0 \\ &=0 \end{aligned}

따라서,

\{1, \cos t, \cos2t, ..., \cos nt, \sin t, \sin 2t, ..., \sin nt\}

는 $W$ 의 orthogonal basis입니다.

Property

\langle \sin kt, \sin kt \rangle = \langle \cos kt, \cos kt \rangle = \pi

Proof

$\langle \sin kt, \sin kt \rangle$

\begin{aligned} \langle \sin kt, \sin kt \rangle &=\int_0^{2\pi} \sin kt \sin kt dt = \int_0^{2\pi}\sin^2ktdt = \int_0^{2\pi}\frac{1-\cos 2kt}{2}dt \\ &= \left[\frac{1}{2}(1-\frac{1}{4k}\sin 2kt)\right]^{2\pi}_0 \\ &=\pi \end{aligned}

$\langle \cos kt, \cos kt \rangle$

\begin{aligned} \langle \cos kt, \cos kt \rangle &=\int_0^{2\pi} \cos kt \cos kt dt = \int_0^{2\pi}\cos^2ktdt = \int_0^{2\pi}\frac{1+\cos 2kt}{2}dt \\ &= \left[\frac{1}{2}(1+\frac{1}{4k}\sin 2kt)\right]^{2\pi}_0 \\ &=\pi \end{aligned}

Jaehyun_onelion

데이터 분석가 새싹

이전 포스트

6.7 Application : Linear regression

다음 포스트