이번에는 AutoMixedPrecision에 대해서 알아보겠습니다. AutoMixedPrecision이란 NVIDIA와 BAIDU에서 연구하고 ICLR에 발표한 논문인 Mixed Precision Traing을 바탕으로 발전된 내용입니다. 이 부분의 내용은 NVIDIA의 블로그를 참고하여 작성하였습니다. 오늘은 이 Mixed Precision을 살펴보고 이 방법을 사용하면 어떠한 장점이 있고 어떻게 사용하는것인지에 대하여 알아보겠습니다.
https://developer.nvidia.com/blog/mixed-precision-training-deep-neural-networks/
nvidia 블로그
우선 이 Mixed Precision을 이해하기 위해서는 Floating Point에 대해서 알아야합니다. Floating Point는 한글로는 부동 소수점이라 부르며 컴퓨터 공학에서 기본적으로 배우는 내용 중 하나입니다. 컴퓨터에서는 숫자를 이진법으로 표시하기 때문에 표현할 수 있는 수의 범위가 정해져 있습니다. 정수의 경우 이렇게 수의 범위가 결정이 되어있어도 큰 문제는 없지만 실수의 경우는 다릅니다. 실수는 숫자의 개수가 무한하기 때문에 컴퓨터에서 모든 실수를 완벽하게 표현할 수 없습니다. 따라서 필요한 것이 Floating Point 개념입니다. 우리가 수를 나타낼 때에는 10진법으로 나타내는데, 이를 이진법으로 바꿔서 표현한 뒤, 정규화하며 2의 지수를 곱해주는 형태로 변환합니다.
예를 들자면 다음과 같습니다.
5.6875를 2진법으로 나태내면 101.1011입니다. 이를 1.011011 x 2^2 로 나타내는 것을 정규화라고 부릅니다.
이때 1.011011을 가수부(exponent), 2의 지수인 2를 정수부(fraction)이라고 합니다.

그림1. 부동소수점 형식
부동소수점 방식은 IEEE754 표준이 가장 널리 쓰이고 있는데 종류는 다음과 같습니다.
-
FP32(Single Precision - 단정밀도)
-
FP64(Double Precision)
-
FP128(Quadruple Precision)
-
FP16(Half Precision)
| 부동소수점 방식 | 부호 | 지수 | 가수 |
|---|---|---|---|
| FP32 | 1bit | 8bit | 23bit |
| FP64 | 1bit | 11bit | 52bit |
| FP128 | 1bit | 15bit | 113bit |
| FP16 | 1bit | 5bit | 10bit |
위의 표는 IEEE 754 표준을 따르는 Floating Point 표기법을 나타낸 것입니다. 주로 32-bit Floating Point를 사용하고 있고 이를 단정밀도라고 부릅니다. 더 세밀하게 값을 표현 하기 위해서는 64bit 혹은 128bit를 사용하기도 합니다. 하지만 어떠한 방식을 사용한다고 하더라도 실수를 오차가 없이 표현하는것은 불가능합니다. 반대로 더 적은 bit로 수를 표현할 때에는 16bit를 사용하는 Half Precision을 사용합니다.
Single Precision이 가지는 문제점
DeepLearning 학습을 진행하다보면, 더 깊은 네트워크를 구성하며 모델의 사이즈가 점점 커지고 있습니다. 모델의 사이즈가 점점 커지다보면 계산에 필요한 메모리의 크기가 더욱 더 커져야합니다. 또한 이렇게 되면 시간도 오래걸리게 됩니다. 또한 Single Precision의 경우 하나의 숫자를 표현하는데 32bit의 공간이 필요하기 때문에 Half Precison에 비해서 더욱 더 큰 메모리가 필요하게 됩니다.
그렇다면 Single Precison을 Half Precision을 사용한다면 어떻게 될까요? Bit 수가 32에서 16으로 줄어들게 되면서 숫자를 표현 할 수 있는 범위가 줄어든 반면 계산량과 메모리의 사용량을 줄일 수 있게 될것입니다.
https://developer.nvidia.com/blog/mixed-precision-training-deep-neural-networks/
출저 : NVIDIA 블로그
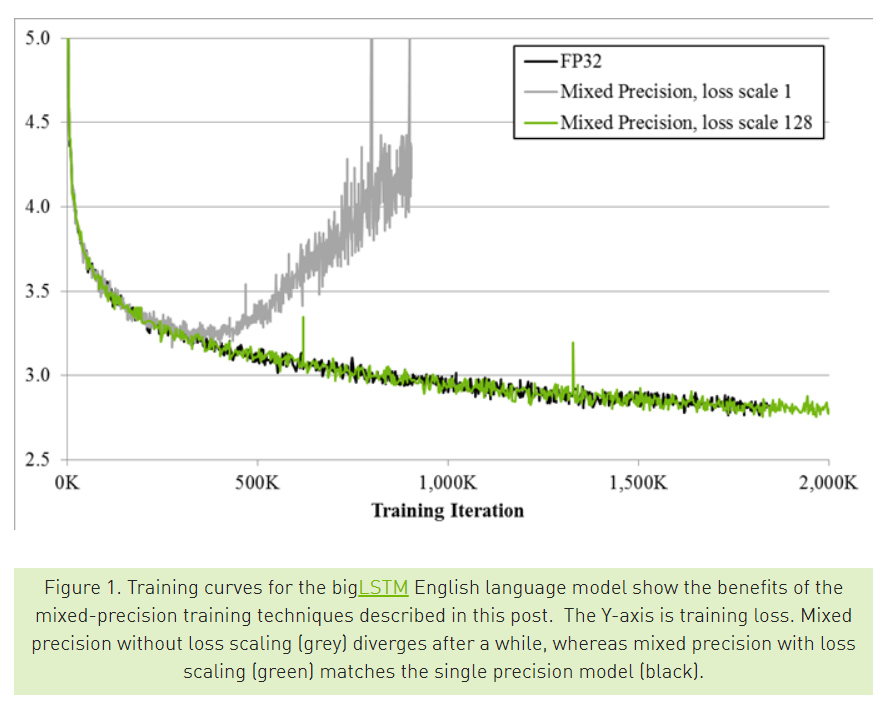
위의 그림에서 검정색 선은 FP32를 이용해 학습시킨 결과 , 회색 선은 FP16을 이용해 학습 시킨 결과입니다. Y축은 training loss인데, FP16을 통해서 학습을 하면 loss가 줄어들다가 수렴하지 못하고 다시 커지는 문제를 확인 할 수 있습니다.
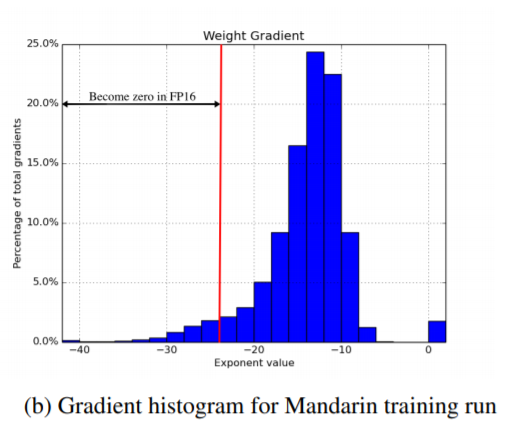
위의 그림은 실제로 FP32를 이용해 네트워크를 학습시키고, 임의의 graident 값들을 sampling 한 결과입니다. 빨간선 왼쪽 gradient들dms FP16에서 표현 불가능한 정밀도의 값들이기 때문에, FP16에서는 0으로 표현이 됩니다. 따라서 이러한 값의 오차들이 누적이 되고 누적되어 학습을 어렵게 합니다.
따라서 FP32와 FP16의 장점을 혼합하여 Mixed Precision 방식을 제안하게 됩니다.
Mixed Precision
Mixed Precision 방법을 간단히 설명하자면 처리 속도를 높이기 위해서 FP16과 정확도 유지를 위해서 FP32를 섞어 학습하는 방법입니다. 실제로 Tensor Core를 활용한 FP16연산을 이용하면 FP32 연산대비 절반의 메모리 사용량과 8배의 연산 처리량과 2배의 메모리 처리량 효과가 있습니다.
Mixed Precision 방식의 작동 방법에 대해서 알아보겠습니다. Deep Neural Network에서 학습에 관여하는 Tensor는 총 4가지입니다. Activation , Activation Gradient, Weights, Weight Gradients입니다. 실제로 실험을 해보았을 때, FP16으로 학습 시켰을 시 Weights, Weight Gradients의 경우 FP16의 범위 안에서 연산이 가능한 경우가 대부분이었다고 합니다. 다만 일부의 network에서 굉장히 크기가 작은 Activation Gradients값이 관찰되었고, FP16이 나타낼 수 있는 값들은 0으로 강제 변환이 되었습니다.
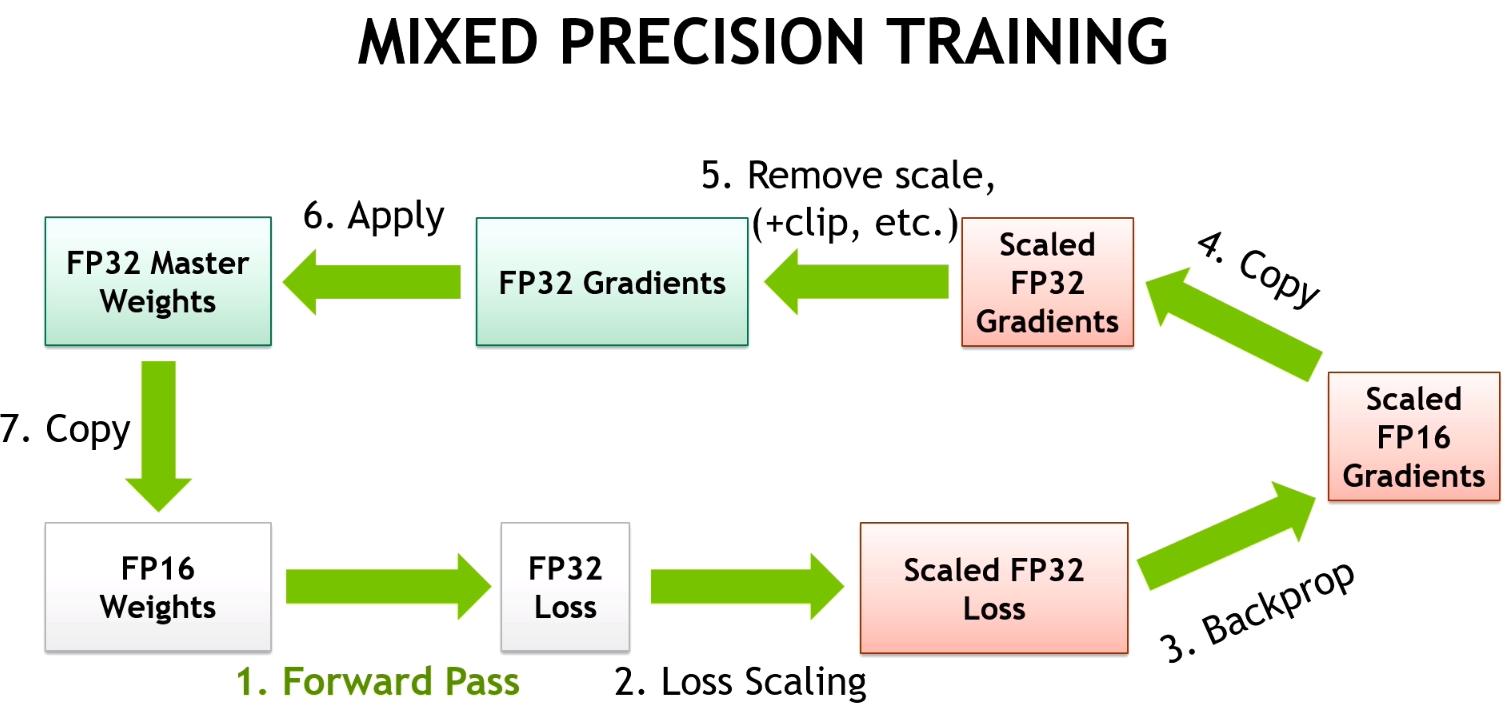
Mixed Precision 동작 순서
- FP32 weight를 FP16 copy weight로 만들어 줍니다.
이 FP16 copy weight는 forward pass, backward pass에 사용이 됩니다.
- FP16 copy weight을 이용해서 forward pass를 진행합니다.
- forward pass로 계산된 FP16 prediction값을 FP32로 캐스팅합니다.
- FP32 prediction을 이용해 FP32 loss를 계산하고, 여기에 scaling factor S를 곱합니다.
- scaled FP32 loss를 FP16으로 캐스팅합니다.
- scaled FP16 loss를 이용하여 backward propagation을 진행하고, gradient를 계산한다.
- FP16 gradient를 FP32로 캐스팅하고, 이를 scaling factor S로 다시 나눕니다.
- FP32 gradient를 이용해 FP32 weight를 update합니다.
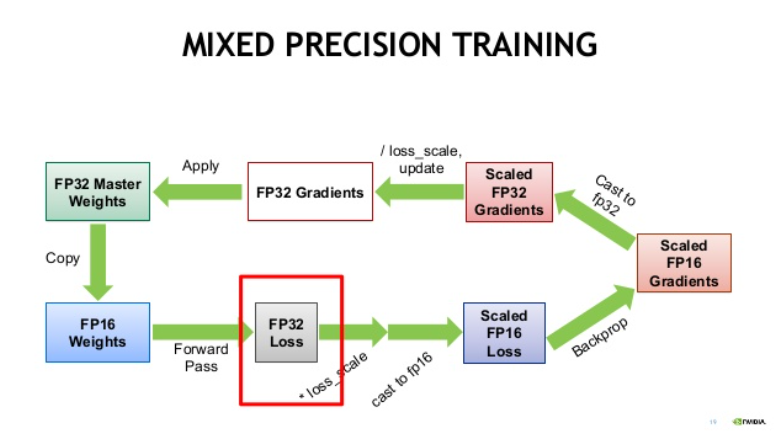
Mixed Precision 동작 방식
즉 FP32 weight의 값을 계속 저장하고 FP16 copy weight를 만들어서 이를 이용해 forward/backward를 진행합니다. 그리고 FP16 copy weight로 얻은 gradient를 이용해 FP32 weight를 업데이트합니다.
Mixed Precision 실험 결과
Mixed Precision 으로 학습을 시켰을 때 정확도 손실이 얼만큼 발생하는지 다룬 실험의 결과를 보겠습니다. 논문의 저자들은 Classification , Object Detection , Speech Recognition , Machine Translation 등 다양한 task에 대해서 Mixed Precision을 적용하여 훈련시키고 결과를 확인했습니다.
속도
매우 빨라지는것을 확인할 수 있다. 최적화가 되어 배치를 늘릴 수 있기 때문에 학습 속도가 빨라 지지만 배치 뿐만 아니라 모델 최적화도 이루어지기 때문에 속도가 증가한다.
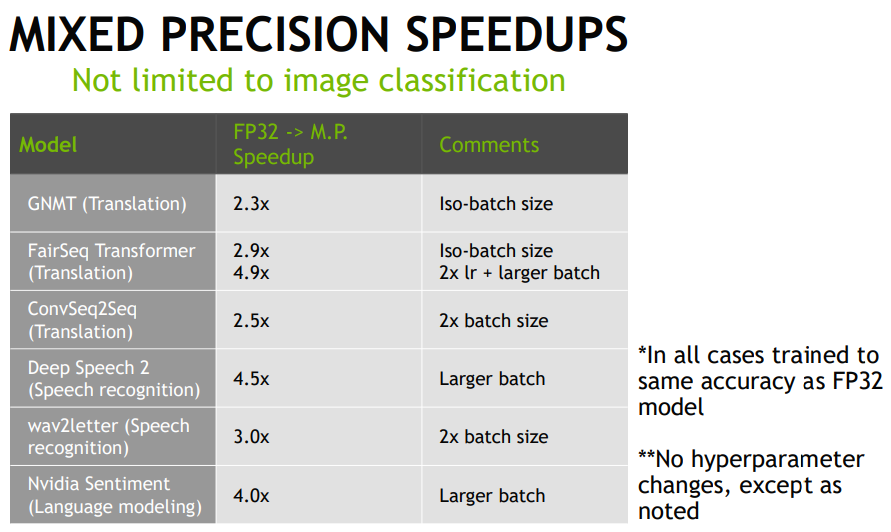
배치 크기가 2배로 증가하지만 속도는 2배 향상이 아닌 2.5배 , 3배씩 증가하는것으로 보아 최적화를 위한 속도 향상도 존재한다는것을 알 수 있습니다.
성능
성능을 살펴보았을 때, 눈에 크게 큰 차이는 없지만 거의 비슷하거나 살짝 향상되는 모습을 보입니다. 그 이유로는 배치사이즈 증가에 의한 학습 효과로 생각이 됩니다.
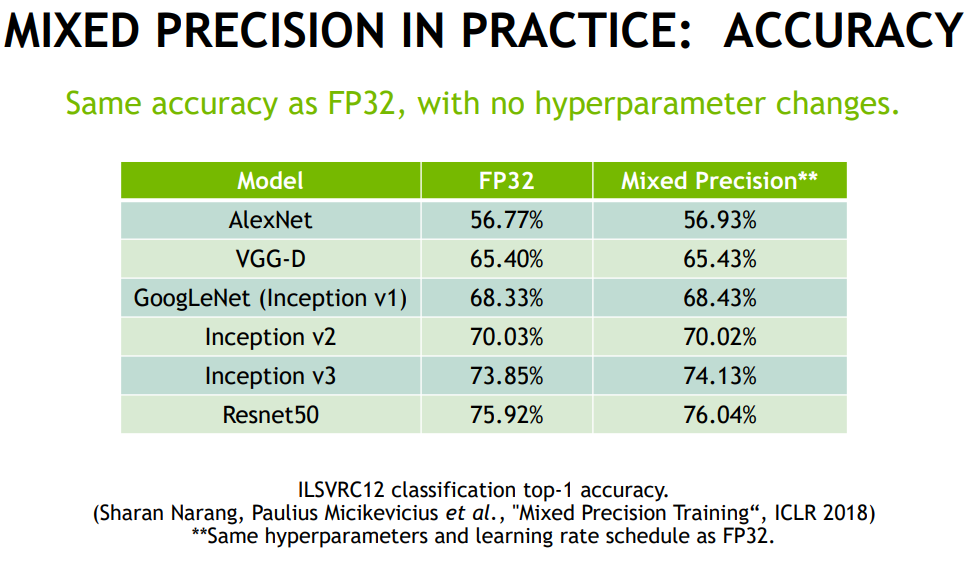
코드
일반 학습 코드
for batch_idx, (inputs, labels) in enumerate(data_loader):
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()Mixed Precision 적용 코드
코드는 https://github.com/hoya012/automatic-mixed-precision-tutorials-pytorch
에서 가져왔습니다.
""" define loss scaler for automatic mixed precision """
# Creates a GradScaler once at the beginning of training.
scaler = torch.cuda.amp.GradScaler()
for batch_idx, (inputs, labels) in enumerate(data_loader):
optimizer.zero_grad()
with torch.cuda.amp.autocast():
# Casts operations to mixed precision
outputs = model(inputs)
loss = criterion(outputs, labels)
# Scales the loss, and calls backward()
# to create scaled gradients
scaler.scale(loss).backward()
# Unscales gradients and calls
# or skips optimizer.step()
scaler.step(self.optimizer)
# Updates the scale for next iteration
scaler.update()학습을 시작하기 전에 scaler를 선언해주고 amp.autocast()를 이용하여 casting 과정을 거치고 forward pass를 진행합니다. backward pass , optimization, weight update 등의 과정이 모두 scaler를 통해서 진행이 됩니다.
실제 적용방법은 다음과 같습니다.
- loss 계산을 해주고, optimizer에 zero_grad를 걸어줍니다.
- scale(loss)로 backward를 진행합니다.
- optimizer step 진행합니다.
마무리
이렇게 Mixed Precision 방식에 대해서 알아보았습니다. Mixed Precision은 Single Precision 방식에 비해서 절반의 메모리를 사용하기 때문에 기존의 사용하던 batch size를 2배로 적용 할 수 있습니다. 만약 OOM를 마주하고 있는 분들이라면 Mixed Precision 방식을 이용해서 OOM 에러도 해결하고 수행속도 향상을 얻을 수 있을 것입니다.