Hypothesis and Cost

(1)의 Hopothesis를 기반하여 실제 모델이 (2)의 실제 값과 얼마큼 차이가 있는가
Simplified hypothesis
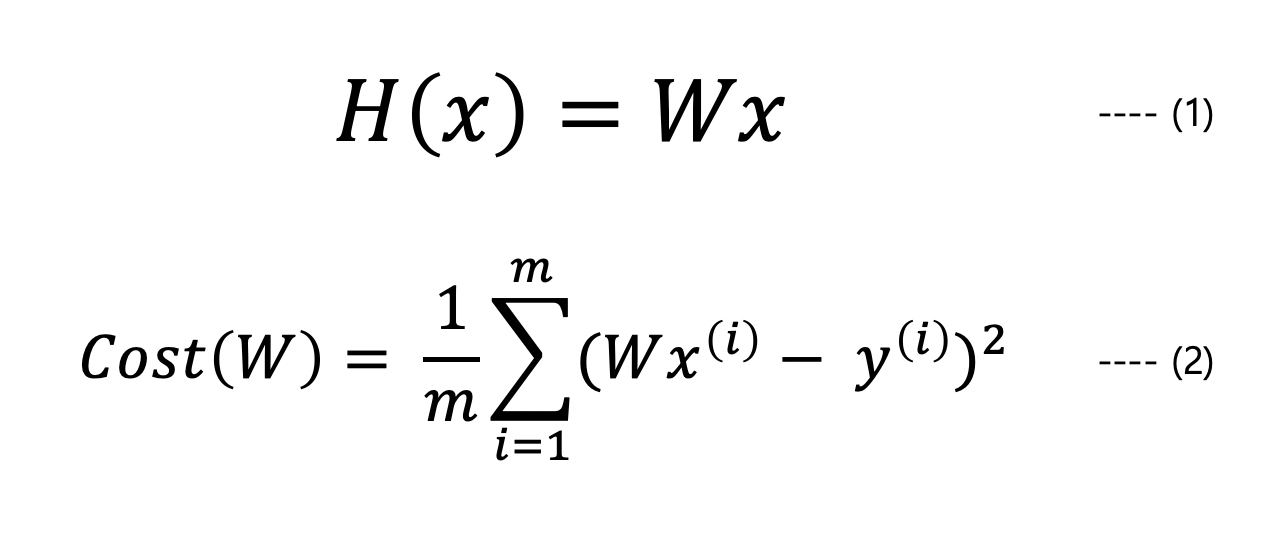
원래 정의했던 Hypothesis에서 b의 값을 제외시켜 간단하게 hypothesis를 정의하여 Cost가 어떻게 될지 구해볼 것이다.
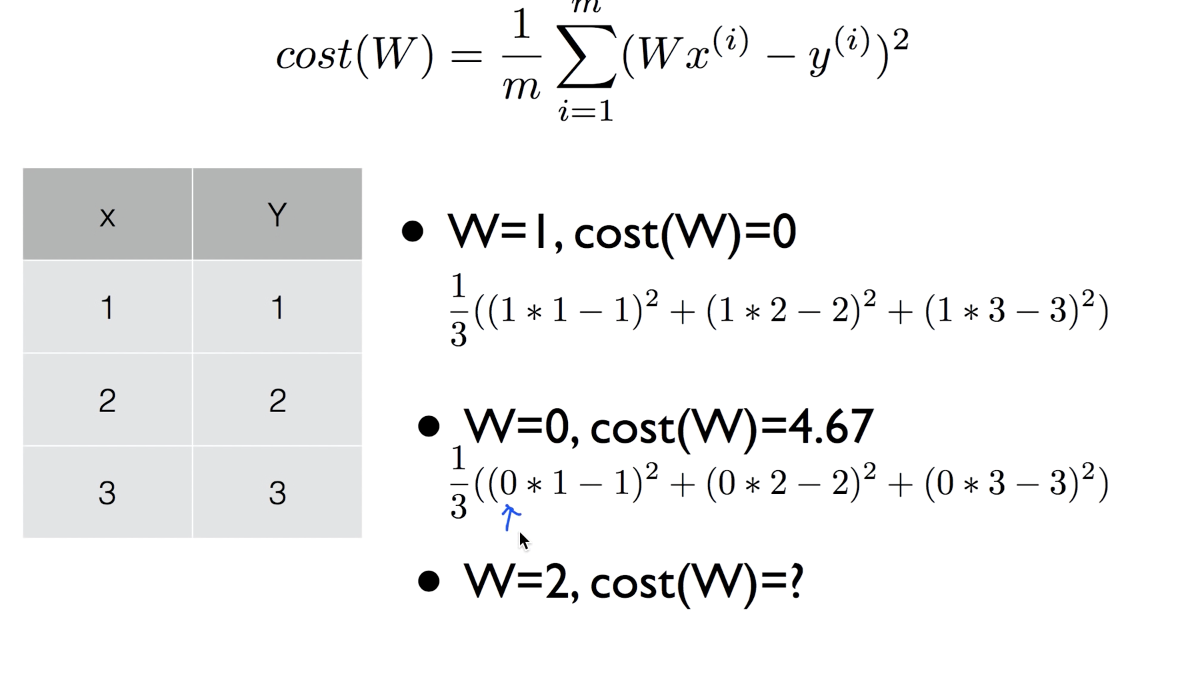
W = 2일 때, Cost(W)의 값은 4.67이 나옴
W의 값에 따라 cost의 그래프를 그리게 되면
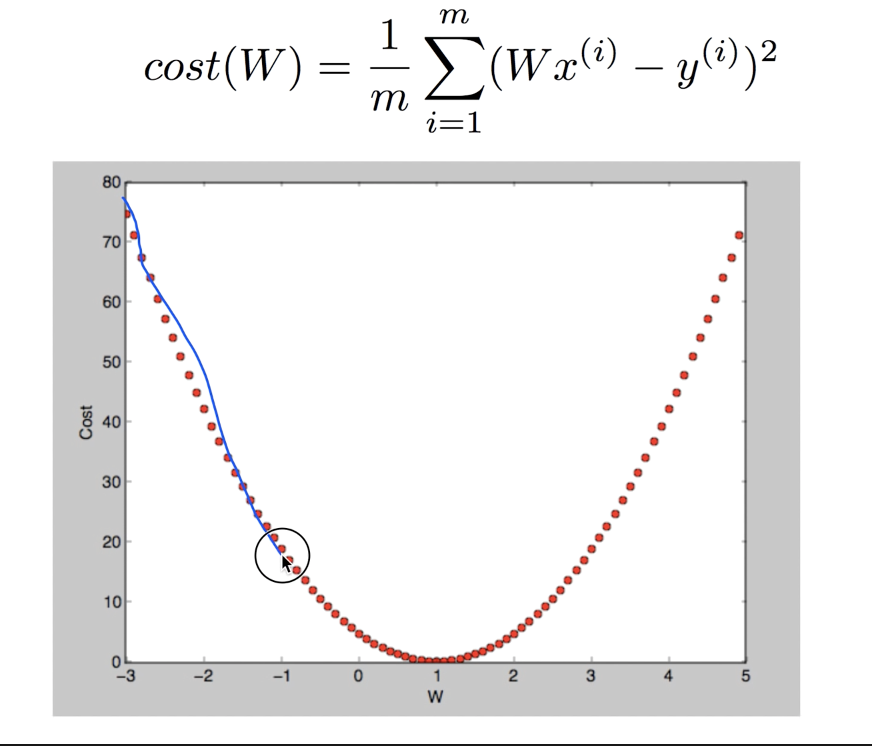
이러한 포물선의 그래프가 나오게 됨.
cost function이 최소화되는 점이 0인 것을 확인할 수 있다.
이 최소화된 점을 찾기 위해서 가장 많이 사용하는 알고리즘은 "Gradient descent algorithm"이다.
Gradient descent algorithm
- 주어진 cost function을 minimize하는데 많이 사용함
- 머신러닝의 Minimize하는데 많이 사용하고, 그 외에도 많이 사용됨
- 우리가 정의한 cost function인 cost(W, b)의 W, b 의 minimize cost를 찾을 수 있음
- Cost(W1, W2, W3 ...)와 같이 많은 cost가 있는 경우에도 적용될 수 있음
How it works?
-
시작점이 5라고 하고 거리의 범위가 1이라고 한다면 5->4->3->2->1->0 순으로 최소값인 0에 도달하게 된다. 따라서 해당 위치에서 경사도를 계산하여 경사도가 있는 범위에 가게되고 경사도가 0이 되는 구간이 minimize cost가 된다.
-
어떤 임의의 점에서 시작하여 W의 값을 변경하고 경사도를 계산하여 cost function이 최소가 되는 점을 찾는다.
-
어떤 점에서 시작하는 간에 항상 최소점에 도달할 수 있다는 것이 장점이다.
-
경사도는 어떻게 구할까?
-> 미분 사용
Fomal definition
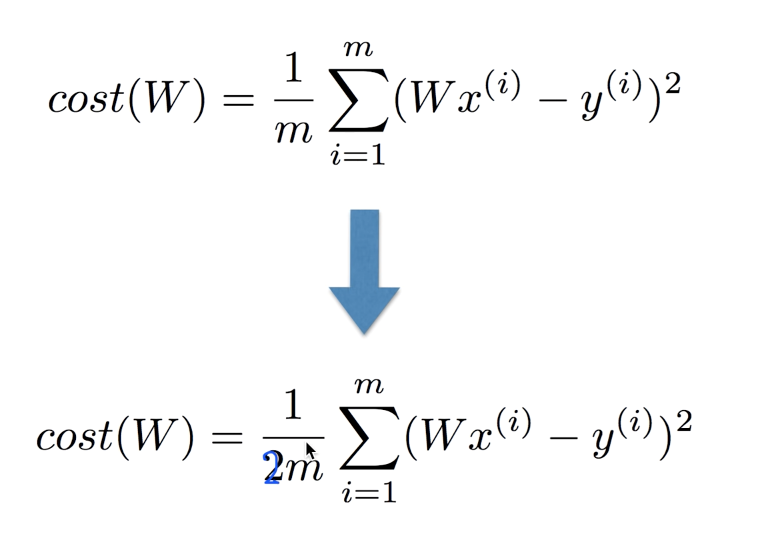
미분을 적용할 때 쉽게 하기 위해서 1/2m 을 사용 (사실, 비슷하긴하나 간단하게 하기위해 사용)
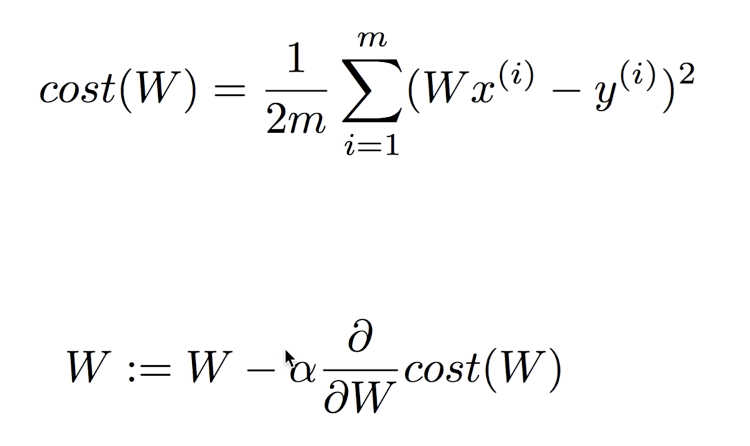
- 알파: learning rate
W를 기준으로 기울기가 양수일 때 값의 범위는 -가 되므로 W의 -방향으로 움직여서 기울기를 구하겠다는 것이고,
기울기가 음수일 때는 기울기의 값이 -가 되어 W:= W - (-)가 되어 즉, +의 값이므로 그래프에서 W의 +방향으로 기울기를 구하겠다는 식이다.
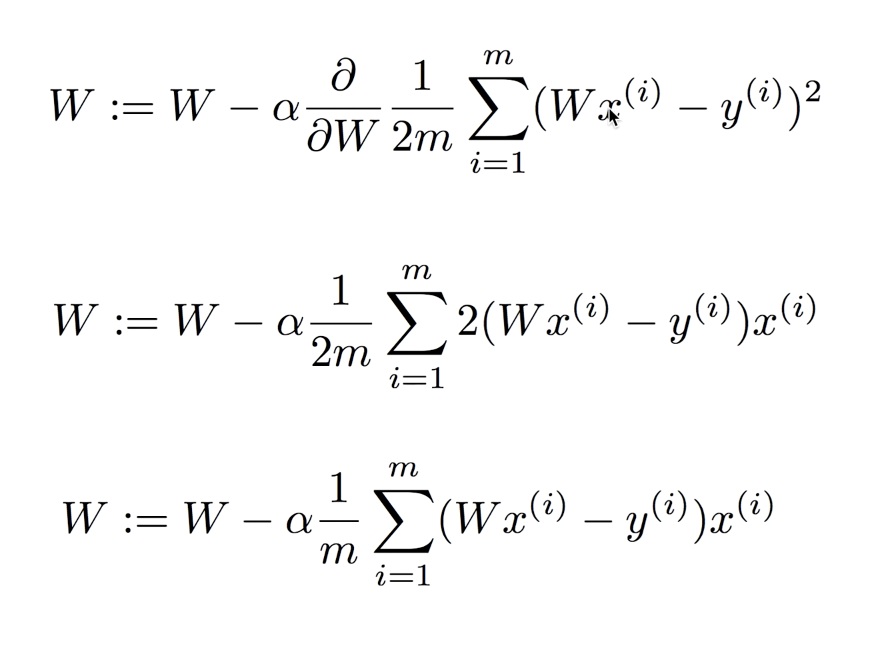
위의 사진은 미분하는 절차다.
따라서 마지막 식이 우리가 원하는 최종 식이 된다.
실행시키게 되면 W의 값이 변화가 되는데 Cost를 minimize한 식을 구할 수 있게 된다.
Convex function
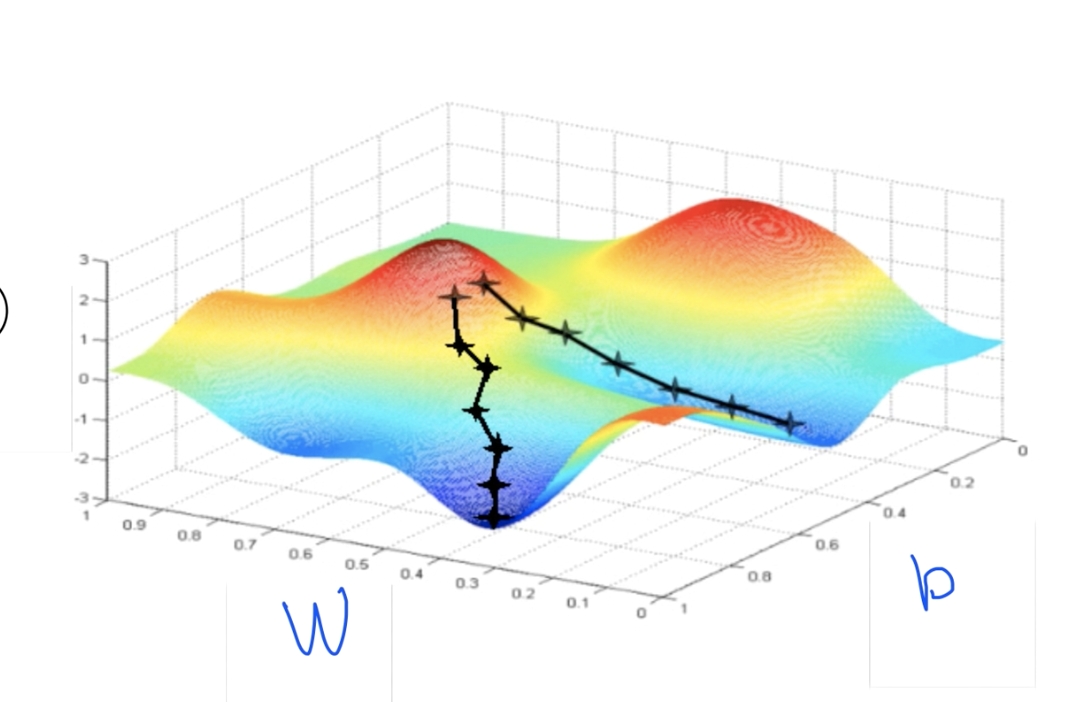
위의 사진은 Cost function을 3차원으로 그려보았을 때이다.
한 발짝씩 내려가는 알고리즘에 대해서는 위 그림과 같이 시작점에 따라서 최소값에 대한 값의 결과가 다르게 나올 수 있다.
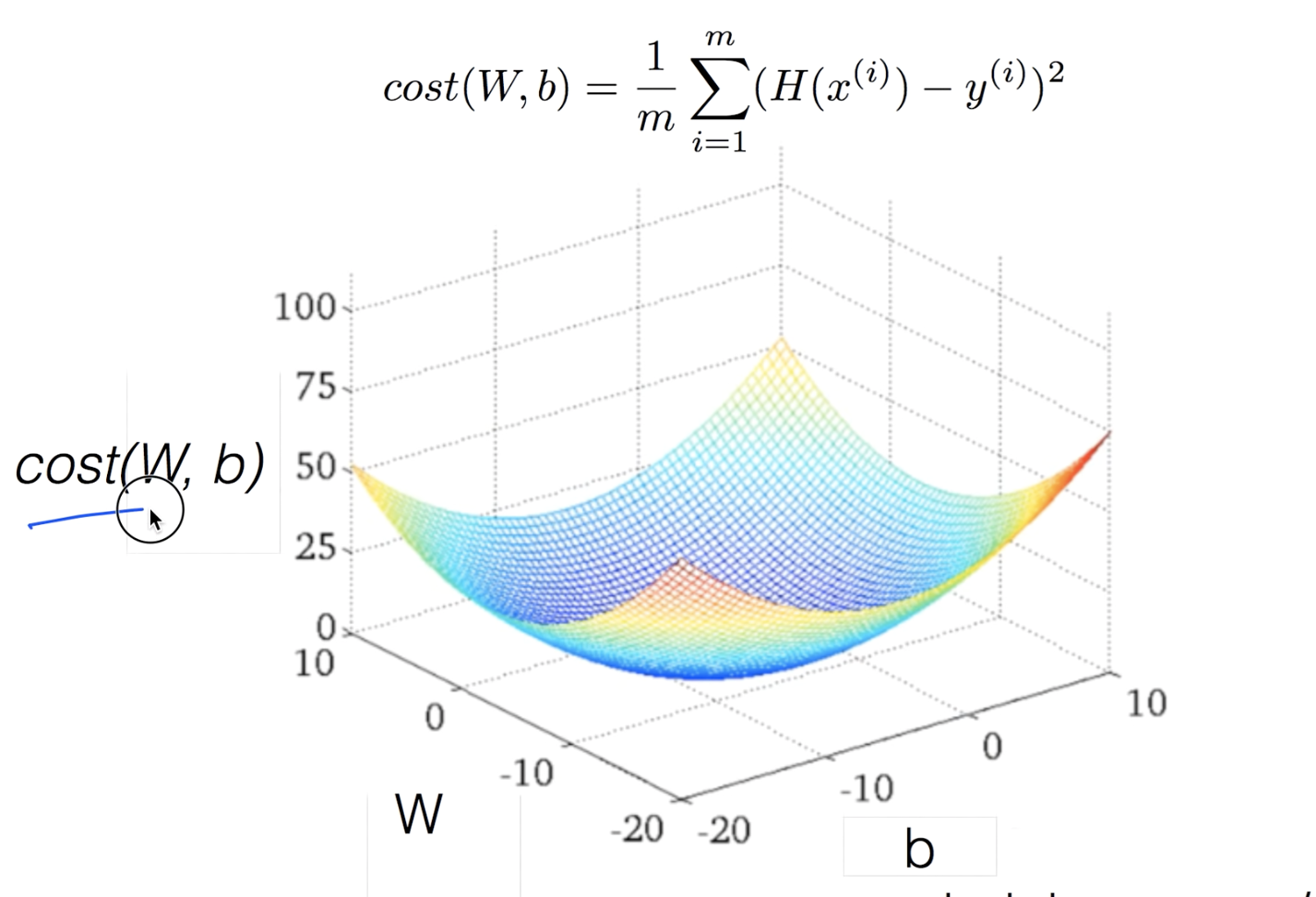
Cost(W,b)의 hopothesis를 가지고 3차원을 그리게 되면 위와 같은 convex function이 그려지게 된다. 어느 지점에서 시작을 하든 최솟값에 도달하게 된다. 이러한 모양이 만들어지는지 확인을 해야한다.
