Node2vec

Node2vec은 2016년 논문으로,

Node Embeddings

Node Classification, Link Prediciton 등의 task를 수행하기 위해 node와 edge의 정보를 담은 representation이 필요하다

• 전문 지식에 기반한 domain-specific feature의 직접 생성 : hand-engineering (일일히 손으로 만드는 것을 뜻하는 듯하다)
  --> 다른 task에 활용 어려움 (domain-specific하게 만들어졌기 때문)

• 학습을 통한 feature 생성: objective funciton을 정의하고 computational efficiency와 predictive accuracy 사이의 균형을 맞춘 optimization으로 task-independent(genral) representation 생성
  --> PCA, Multi-Dimensional Scaling 등 eigen decomposition을 포함하는 기존 방법으로는 좋은 representation을 얻기 어렵고 계산비용이 크다. 그러므로 그래프 구조 및 이웃 정보를 잘 보존하는 동시에 효율적으로 optimization을 수행하는 방법이 필요하다 --> "node2vec"

결국, Node2vec의 목표는
1. Neighborhood context를 잘 반영
2. 기존 방법에 비해 계산비용이 낮음
3. Domain / Downstream Task에 따라 별도의 hand engineering이 필요하지 않음
위 조건들을 만족하는 Embedding Framework를 만드는 것이 된다.

Node Similarity를 고려하는 두 가지 관점

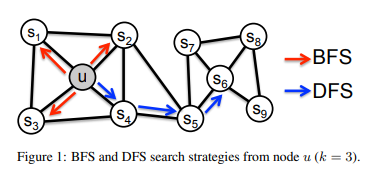
1. Graph Homophily

Graph Homophily는 이웃해 있는 노드끼리의 성질이 유사함을 뜻한다. 위 그림에서 graph homophily를 고려하면 노드 u와 유사한 노드는 s1, s2, s3, s4가 되고, 이를 고려한 그래프 탐색 기준을 BFS(Breadth First Search : 넓이 우선 탐색)이라고 한다.

2. Structural Equivalence

Structural Equivalence는 노드 간 거리가 멀더라도 비슷한 구조를 가진 노드끼리의 성질이 유사함을 뜻한다. 위 그림에서 structural equivalence를 고려하면 노드 u와 유사한 노드는 s1~s4가 아닌 s6이 된다. 이를 고려한 그래프 탐색 기준을 DFS(Depth First Search : 깊이 우선 탐색)이라고 한다.

Node2vec의 Feature Learning

node2vec은 NLP 분야에서 사용하는 Word2vec, 그중에서도 skip-gram의 학습 방식을 채용했다. skip-gram은 주어진 문장 시퀀스에서 중심 단어를 통해 주변 단어를 예측하는데, Node2vec은 중심 노드를 통해 주변 노드를 예측하는 방식으로 학습되며 목적함수는 아래와 같다

$N_s(u)$는 특정 샘플링 기준 $S$에 의해 추출한 노드 $u$의 이웃 집합이고, 노드 $u$를 $d$차원 벡터로 맵핑시키는 함수 $f(u)$가 $u$의 이웃 노드 집합 $N_s$의 등장 확률을 최대화하도록 학습된다. 등장 확률 $Pr$에 대해 설명하기 전에, 두 가지 전제를 한다.

1. 노드 $u$의 이웃 노드 $n_i$들은 $f(u)$가 주어졌을 때 조건부 독립이다.

그러므로 $u$의 이웃 집합 $N_s$의 등장 확률을 모든 이웃 노드 $n_i$의 등장 확률의 곱으로 표현할 수 있다.

2. Symmetry in feature space

중심 노드와 이웃 노드는 서로에 대해 symmetric effect를 갖는다고 나와있는데, 아마 undirected graph를 전제하는 것으로 이해했다.

이러한 전제 하에, 노드 $u$의 이웃 노드 $n_i$를 관측할 확률을 softmax 함수의 형태로 정의할 수 있다.

이를 다시 node2vec의 목적 함수에 대입하면 다음과 같다

이 때, $Z_u$는 $\sum_{v \in V}{exp(f(u)\cdot f(v))}$이다.

이제 Node2vec이 어떻게 '이웃 관계'를 고려한 임베딩을 만드는지는 알 수 있다. 그런데, 이전에 설명했듯 '이웃'이라는 정의는 Homophily와 Structural Equivalence를 종합적으로 고려(혹은 하나만 고려)해야한다.
$\rightarrow$Node2vec이 neighborhood set $N_S$라는 이웃 시퀀스를 샘플링하는 방법은 아래와 같다.
(이웃 시퀀스를 샘플링하는 방법을 node2vec이 '이웃'관계를 어떻게 정의하는가에 대한 설명으로 봐도 무방하다.)

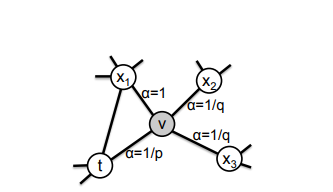
Node2vec의 Sampling Strategy (Random Walk Strategy)

node2vec은 이웃 노드 집합 $N_S$를 Biased Random Walk를 통해 샘플링한다. 이는 그래프의 성질에 따라 random walk strategy를 다르게 설정할 수 있다는 장점이 있다.