Linear Regression(선형 회귀) vs Logistic Regression(로지스틱 회귀)

1. Linear Regression(선형 회귀)
   : input data에 따른 output data의 관계를 1차원 방정식으로 구하는 것

   • Hypothesis

     $H(X) = WX$

   • cost

     $cost(W)=\frac{1}{m} \sum_{}(WX- y)^2$

     

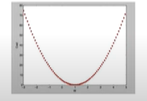
   • Gradient decent

     $W := W - \alpha\frac{\alpha}{\alpha W}cost(W)$

     ---

   • Binary Classification(이진 분류)에서 발생할 수 있는 문제 사항
     :기준선 보다 많이 공부한 사람이 시험에 떨어지고, 기준선 보다 적게 공부한 사람이 시험에 통과하는 상황
     

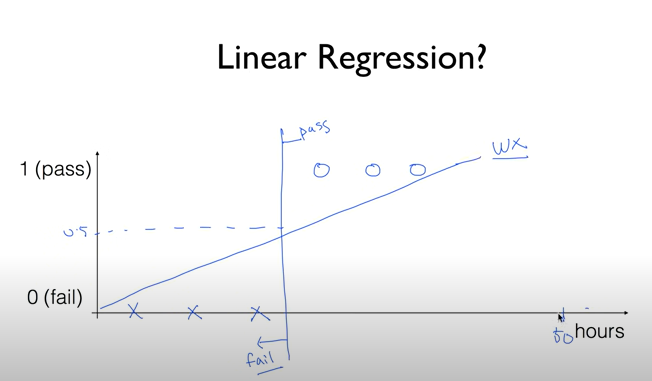
     --> 1, 50, 90 등 여러 가지 값이 도출되는 문제 발생
     But, Logistic Regression을 사용하면 이 값들을 0~1사이 값으로 변환가능

2. Logistic Regression(로지스틱 회귀)
   : input에 따른 output의 관계를 직선으로 알맞게 나타내지 못하는 상황을 보완한 것

   • Binary Classification -> Linear Regression
     아래 식을 사용하여 변환시 Binary Classification = Logistic Regression으로 표현 가능

     $H(X) = \frac{1}{1+e^-W^TX}$

   • cost
     : y=1, y=0일 때를 나뉘어 정의

     $cost(W)=\frac{1}{m} \sum_{}c(H(x),y) \\ c(H(x),y) = \begin{cases} -log(H(x)) & \text{: y = 1}\\ -log(1-H(x)) & \text{: y = 0} \end{cases}$
     $c(H(x),y) = ylog(H(x)) - (1-y)log(1-H(x)) \\ cost(W)=-\frac{1}{m}\sum_{}ylog(H(x)) + (1-y)log(1-H(x))$
     $W := W - \alpha\frac{\alpha}{\alpha W}cost(W)$

     Linear Regression(선형 회귀) vs Logistic Regression(로지스틱 회귀)

     분류	Linear Regression(선형 회귀)	Logistic Regression(로지스틱 회귀)
     	1 ~ 100 사이 값 도출	0 ~ 1 사이 값 도출
     	Binary Classification(이진 분류) 표현 불가능	Binary Classification(이진 분류) 표현 가능
     	Gradient Descent Algorithm 사용시 어디서 시작하든 하나의 최소점에 도달 가능	Gradient Descent Algorithm 사용시 시작하는 곳에 따라서 도달하는 최소점이 여러개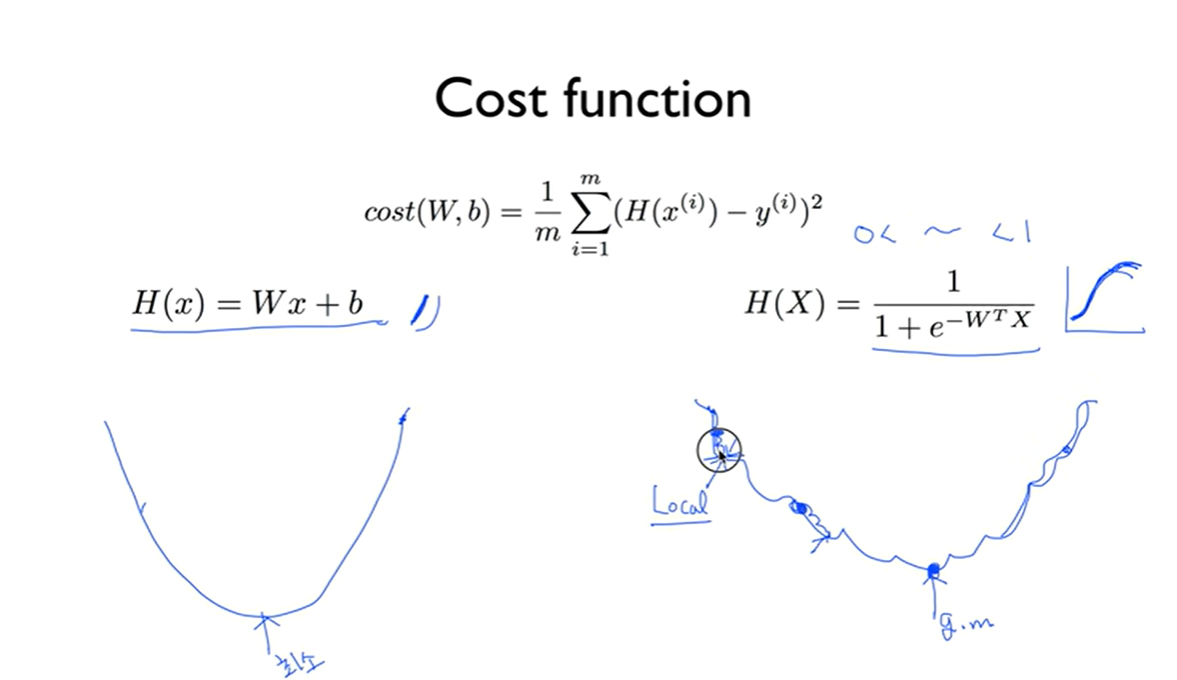