1. AL,ML,DL

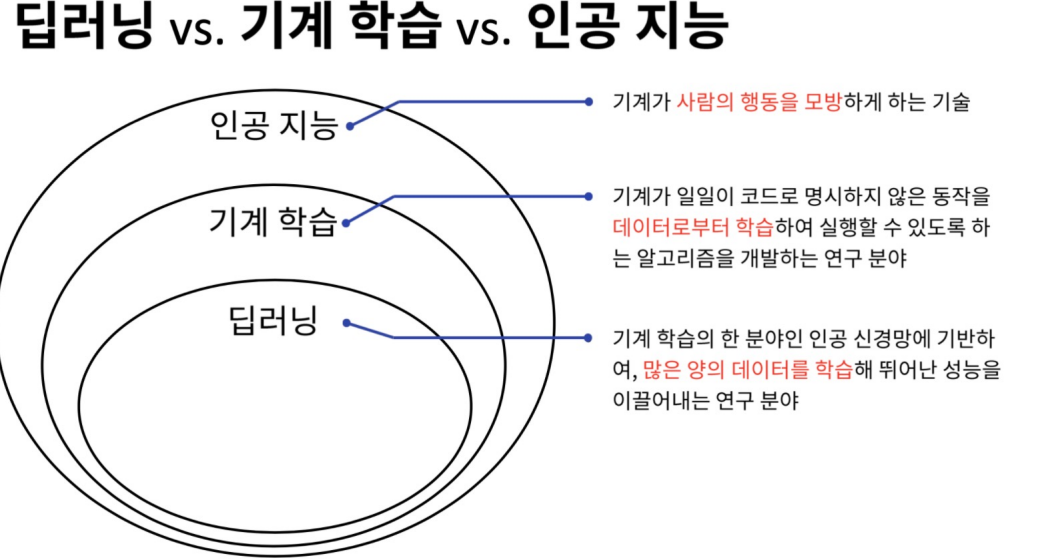
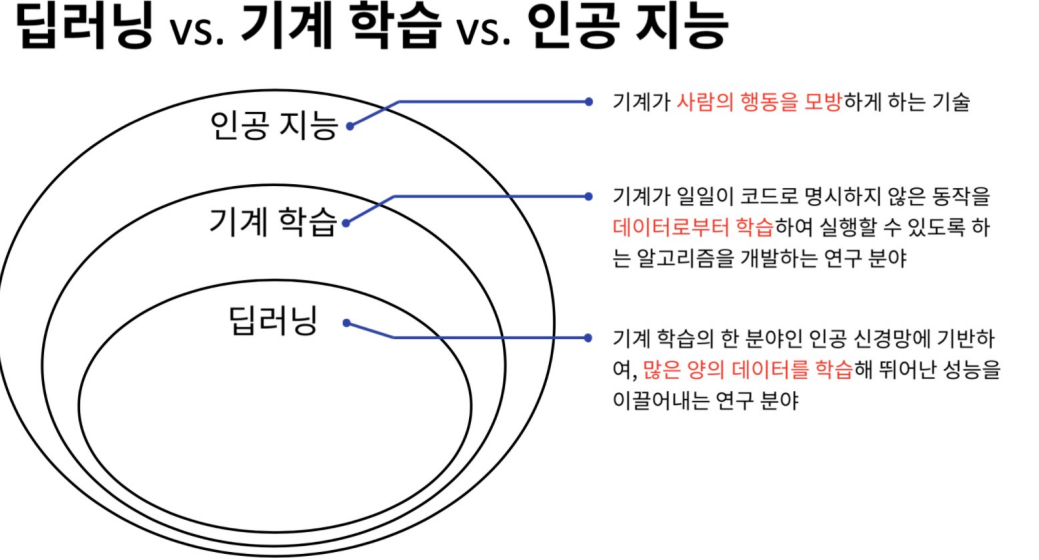
• 인공지능: 기계가 사람의 행동을 모방하는 기술
• 기계 학습: 기계가 일일이 코드로 명시하지 않은 동작을 데이터로부터 학습하여 실행할 수 있도록 하는 알고리즘을 개발하는 연구 분야
• 딥러닝: 기계 학습의 한 분야인 인공 신경망에 기반하여, 많은 양의 데이터를 학습해 뛰어난 성능을 이끌어내는 연구 분야

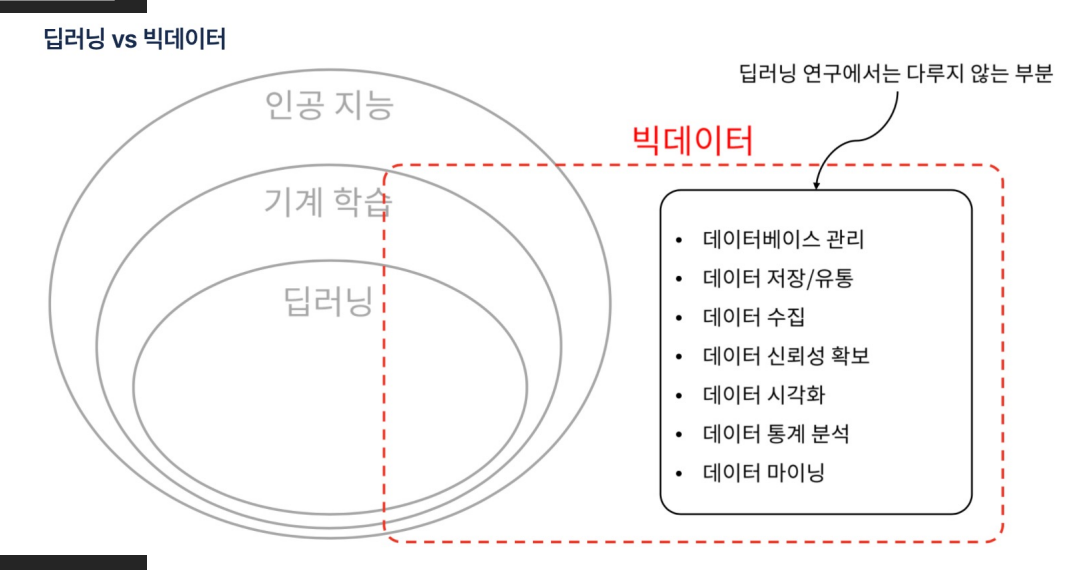
• 딥러닝은 빅데이터를 다루지 않는다.
  
  

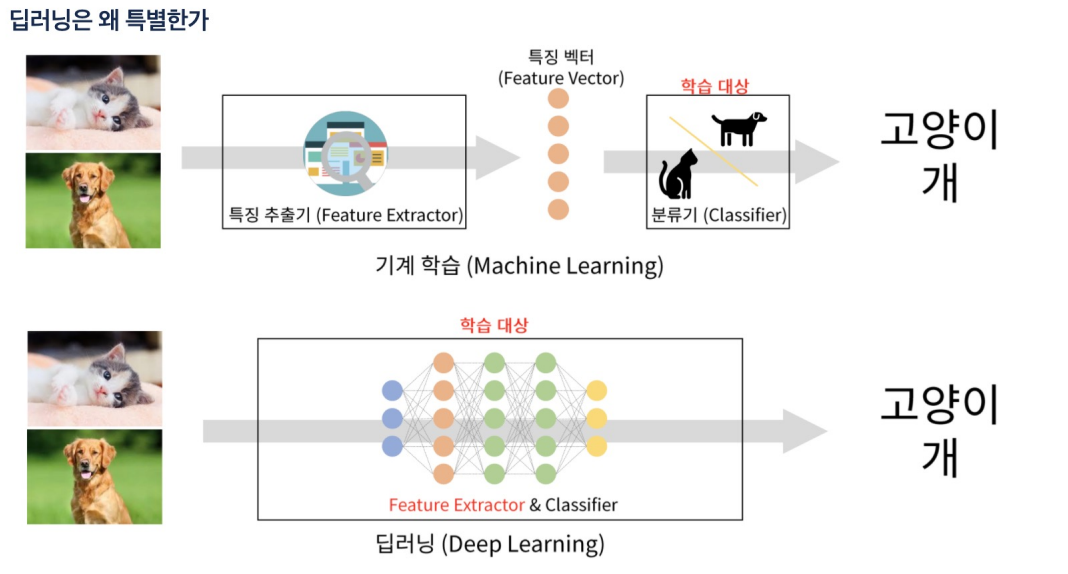
• 영상을 분할하고 영상 해상도 조절
  
  

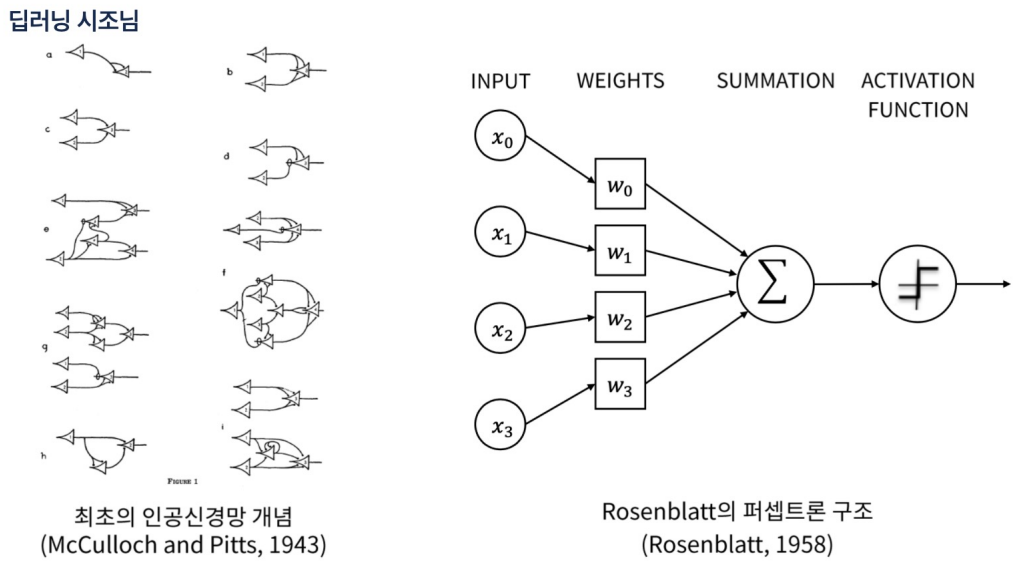
• 여기서 퍼셉트론은 지금의 딥러닝의 뉴런을 뜻한다.
  
  
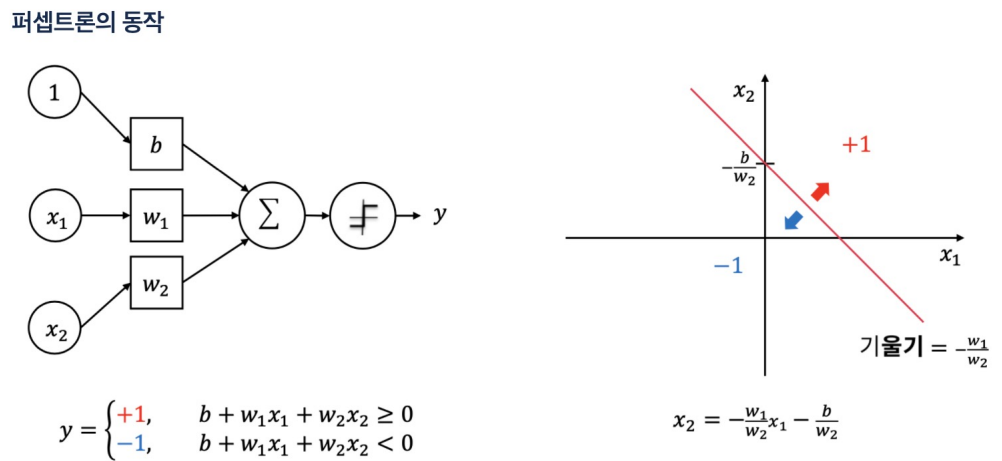
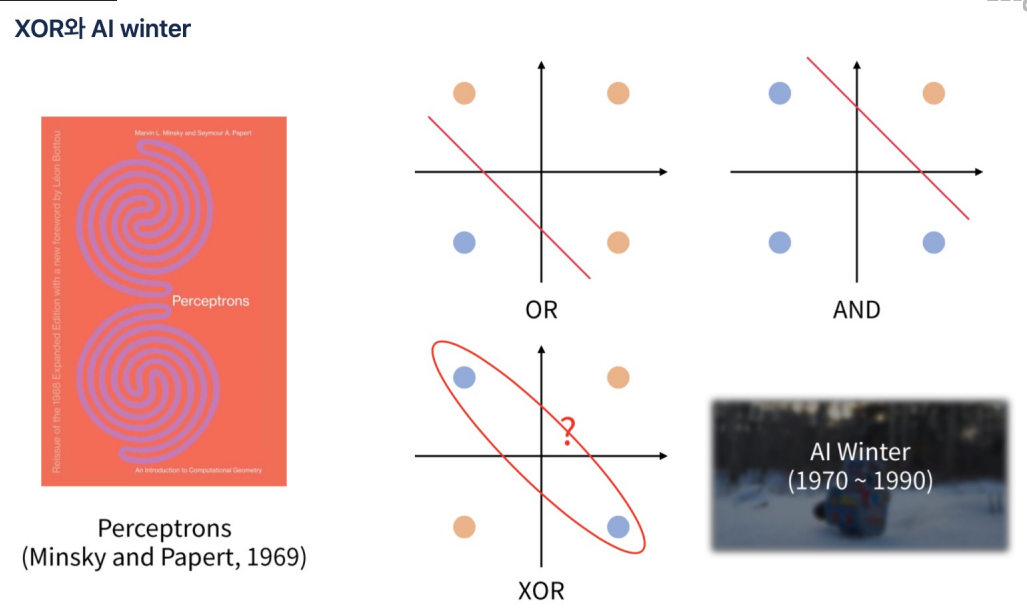
• 잠깐 딥러닝의 XOR을 증명하지 못하는 암흑기가 존재했다.
  
  
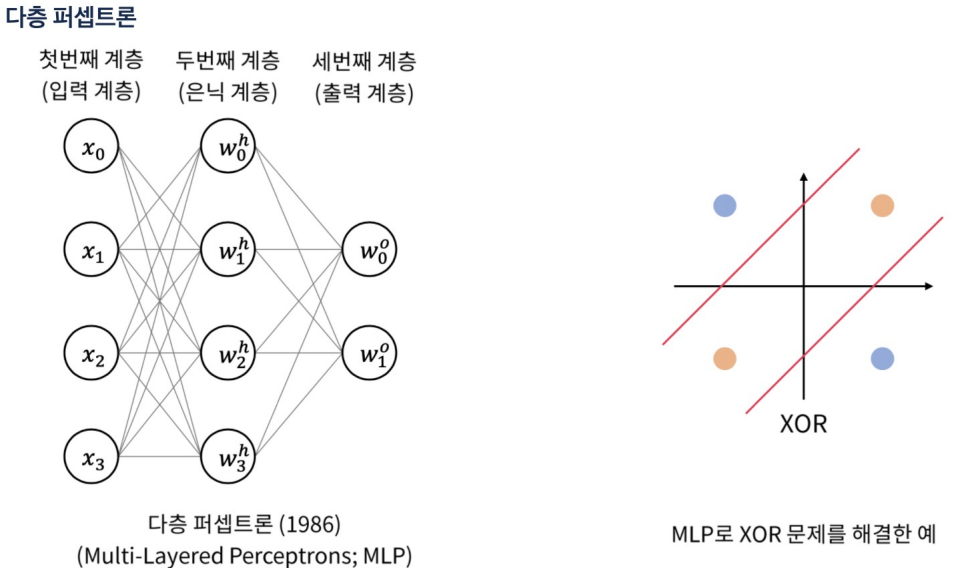
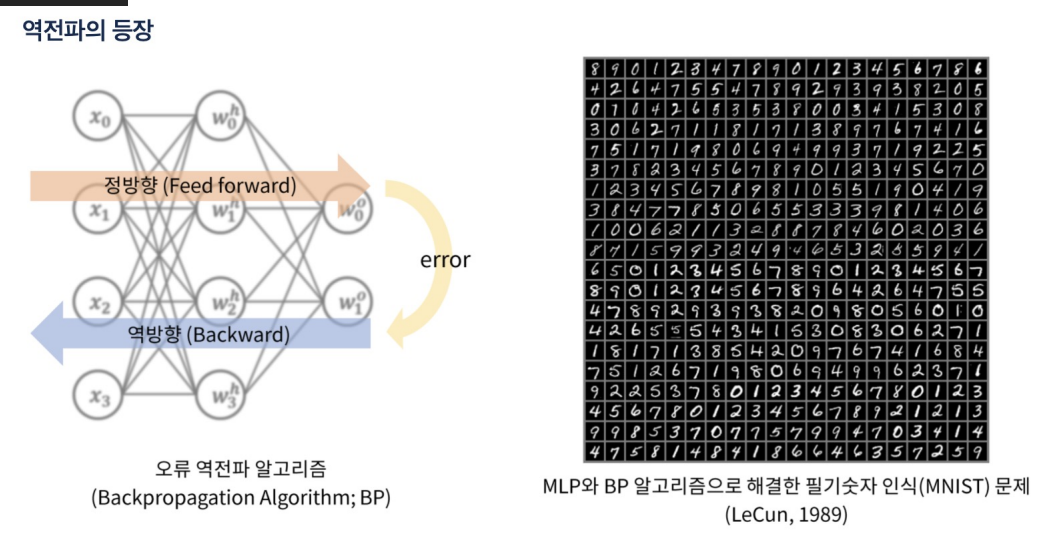
• 역전파의 등장으로 XOR을 오류를 해결했다.
  
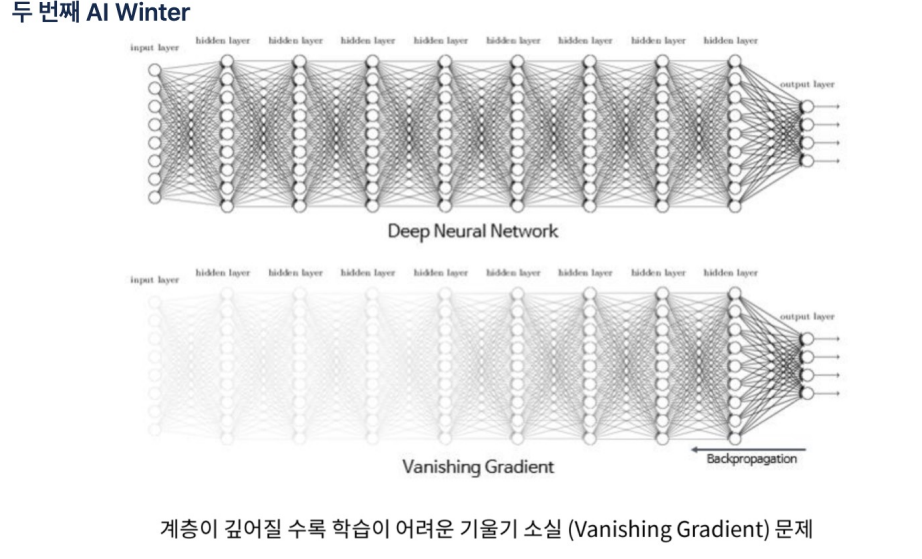
• gradient vanishing문제가 있었는데 이것을 해결하기 위한 여러 가지 방법들이 있다.

1. ReLU (Rectified Linear Unit): ReLU는 음수를 0으로 만들고, 양수는그대로 둔다. 이로 인해 비선형성을 도입하면서도 기울기 소실 문제를 완화
   

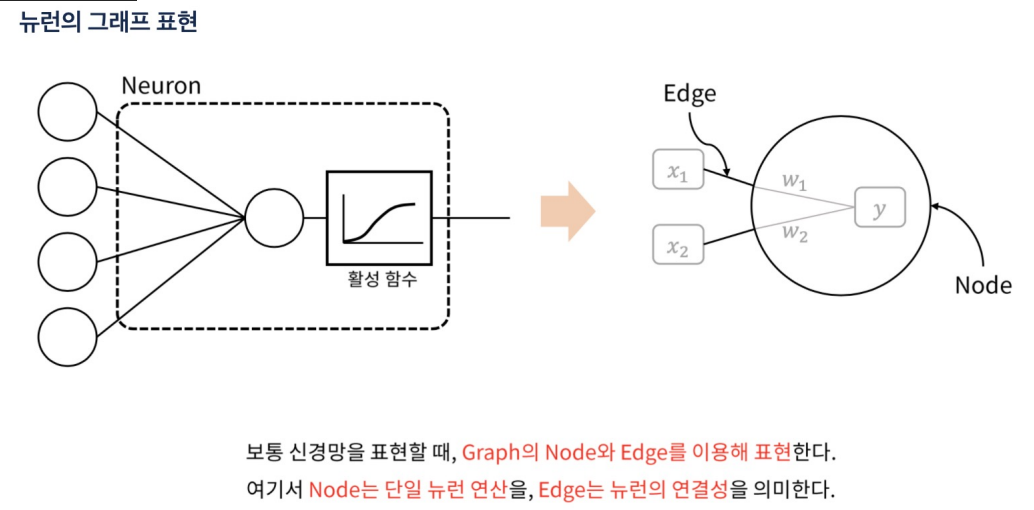
• 뉴런은 인공 신경망(ANN)의 기본 구성 요소이다.
• 뉴런은 신경망에서 다양한 패턴과 관계를 학습하는 역할
• 뉴런은 입력 데이터의 특정 특징에 반응하도록 학습되며, 신경망 전체에서 복잡한 패턴과 관계를 모델링

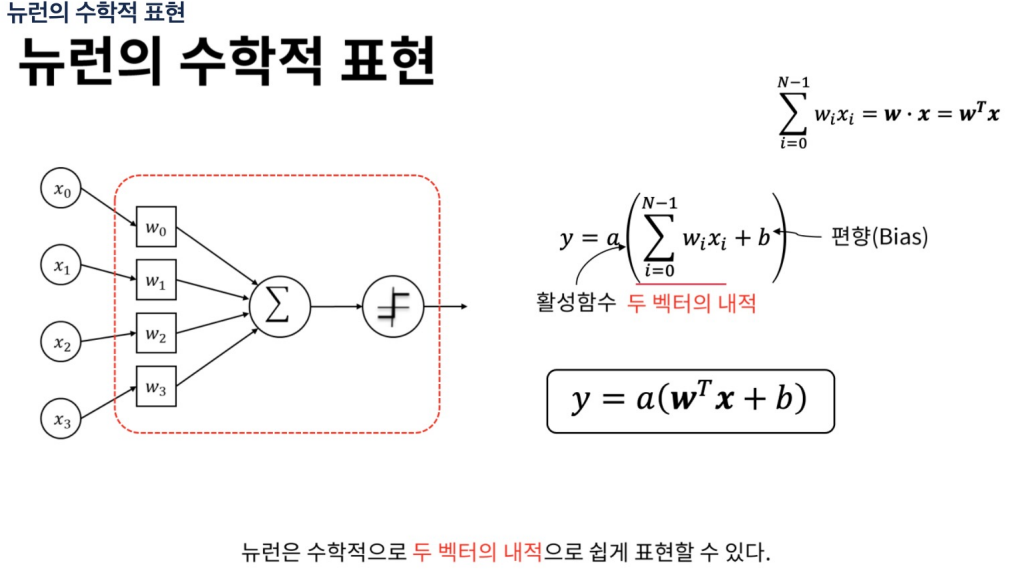
1 입력(Inputs): 뉴런에 들어오는 신호 이들은 다른 뉴런의 출력이거나, 외부 소스에서 온 데이터
2 가중치(Weights): 각 입력에 대해 할당된 가중치. 이 가중치는 해당 입력의 중요도
3 활성화 함수(Activation Function): 가중치가 적용된 입력의 합을 받아들여, 뉴런의 출력을 결정하는 함수
4 바이어스(Bias): 뉴런의 활성화 임계값을 조정하는 역할
5 출력(Output): 뉴런의 최종 출력 신호

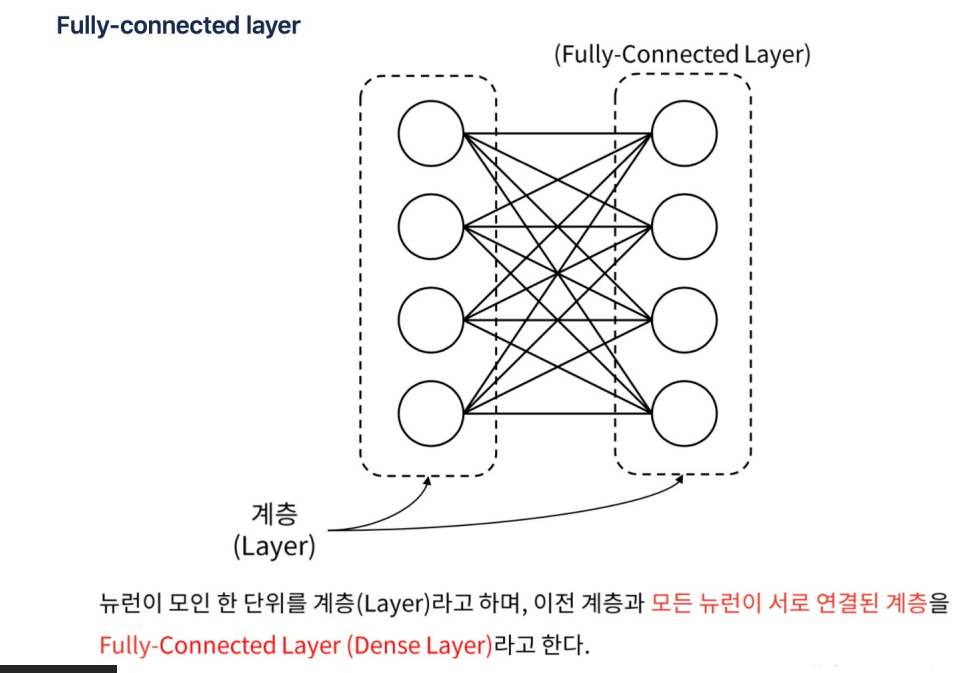
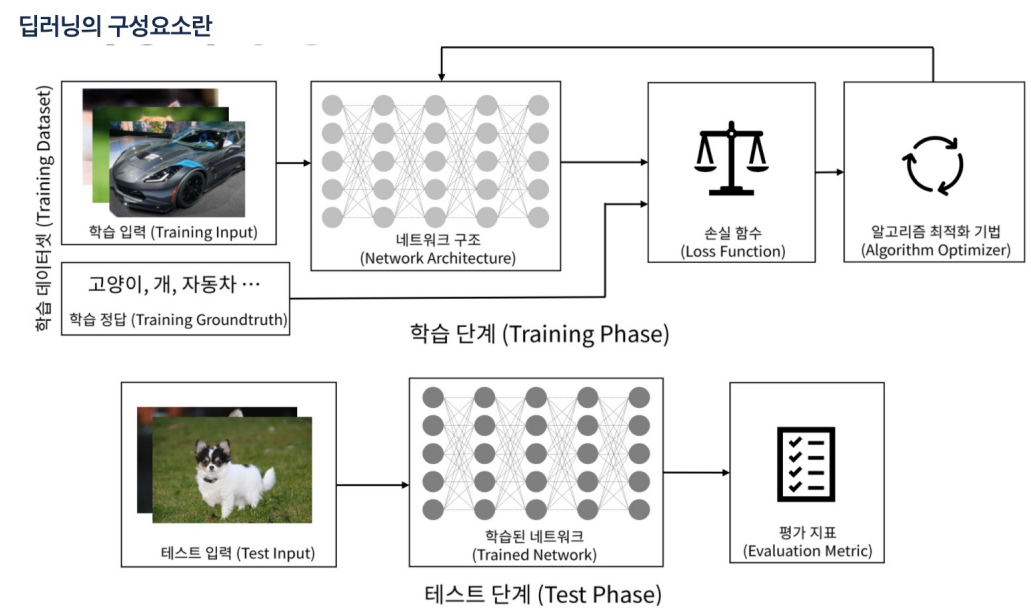
• 레이어: 레이어는 딥러닝 모델에서 데이터를 처리하는 한 단계를 의미
  각 레이어는 여러 개의 뉴런으로 구성되어 있으며, 이 뉴런들은 입력 데이터를 받아 가중치와 활성화 함수를 통해 변환된 후 다음 레이어로 전달
• 딥러닝 모델은 여러 레이어를 쌓아서 구성. 이를 "딥(Deep)"이라고 부르는 이유는 모델에 여러 층의 레이어가 존재
• Dense 레이어:완전 연결 레이어(Fully Connected Layer)는 가장 기본적인 레이어 유형, 이 레이어에서는 모든 입력 뉴런이 모든 출력 뉴런과 연결
• 모든 요소에 대한 가중치를 가지며, 이를 통해 입력 데이터의 선형 변환을 수행
  그 후 활성화 함수를 적용하여 비선형성을 도입
  
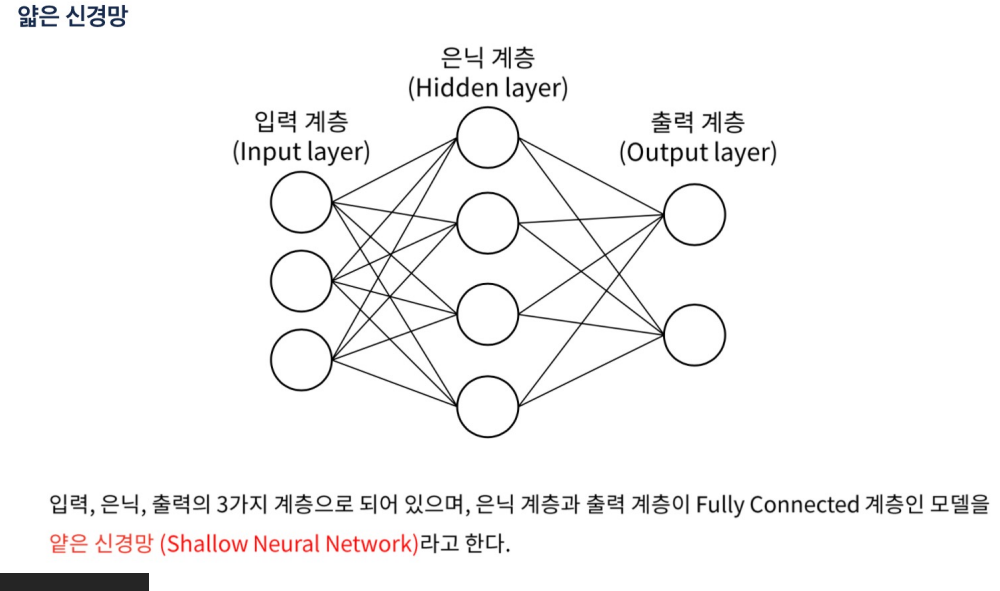
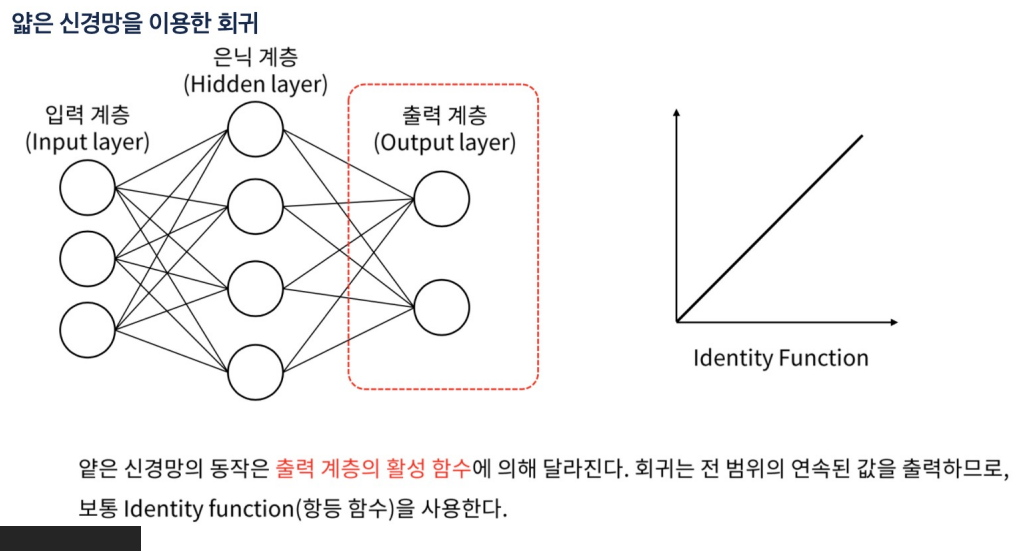
• 얕은 신경망(Shallow Neural Network): 딥러닝 모델 중에서 비교적 적은 수의 은닉층을 가지고 있는 모델을 일반적으로 얕은 신경망은 입력층, 하나 또는 소수의 은닉층, 그리고 출력층으로 구성
• 과적합 위험이 낮다 파라미터가 적기 때문
• 얕은 신경망은 주로 간단한 문제나 데이터가 복잡하지 않을 때 사용
  

---

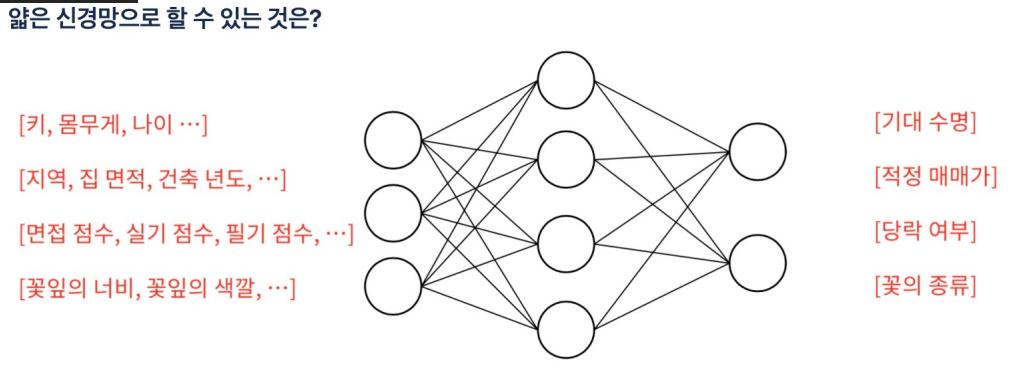
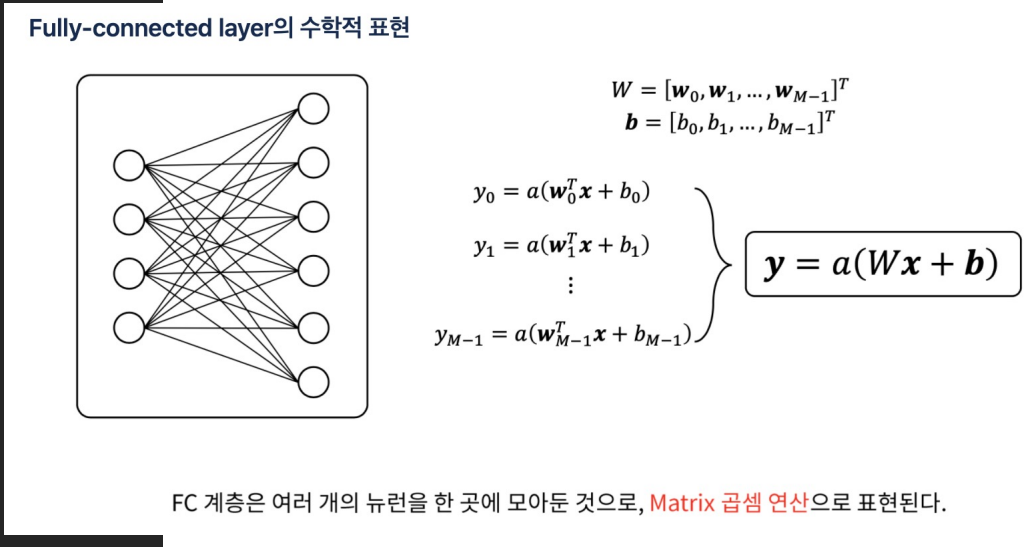
• Fully-conmnected layer(완전 연결 계층) 또는 Dense layer은
  신경망에서 가장 기본적인 레이어이다.

• Fully-connected layer는 입력 데이터가 1차원 배열로 표현될 수 있는 경우에 적합

• 장점: 간단하고 범용적이며 복잡한 관계와 패턴을 학습

• 단점: 많은 파라미터를 가지고 있어서 모델의 크기가 커지고, 과적합의 위험이 있다. 입력 데이터의 크기가 클 때 비효율적
  

• 예를 들어, 28x28 픽셀의 이미지를 입력으로 사용하는 경우, 입력 계층에는 784(28x28)개의 뉴런

• 가중치와 바이어스: 입력 계층의 뉴런은 가중치와 바이어스를 가지고 있지 않다

• 활성화 함수: 입력 계층에는 활성화 함수가 적용되지 않는다.

• 입력 계층은 외부 세계로부터 데이터를 받아들이고, 이를 신경망 내부로 전달
  

• 신경망의 입력 계층과 출력 계층 사이에 위치하는 계층, 이 계층들은 신경망이 복잡한 패턴과 관계를 학습하는 데 도움을 주며, 모델의 예측 능력을 향상

• 은닉 계층의 뉴런 수는 사용자가 정의

• 은닉 계층의 각 뉴런은 가중치와 바이어스를 가지며, 이를 통해 입력 데이터를 변환

• 은닉 계층에는 비선형 활성화 함수가 적용되어, 모델이 복잡한 비선형 관계를 학습

• 무 많은 은닉 뉴런이나 계층을 사용하면 과적합(overfitting)이 발생할 위험이 있으며, 학습 시간이 길어진다.
  

• 모델의 최종 예측 결과를 생성

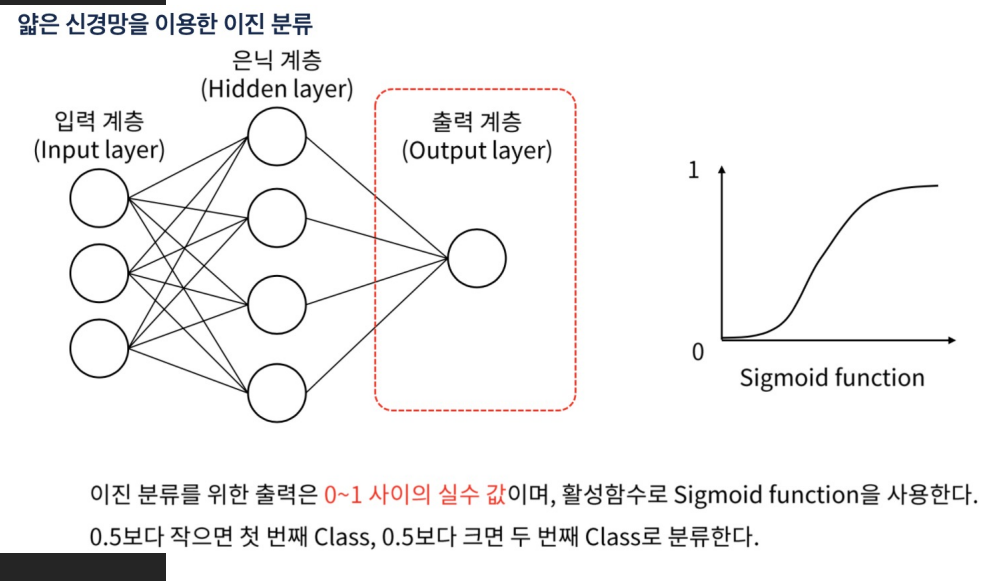
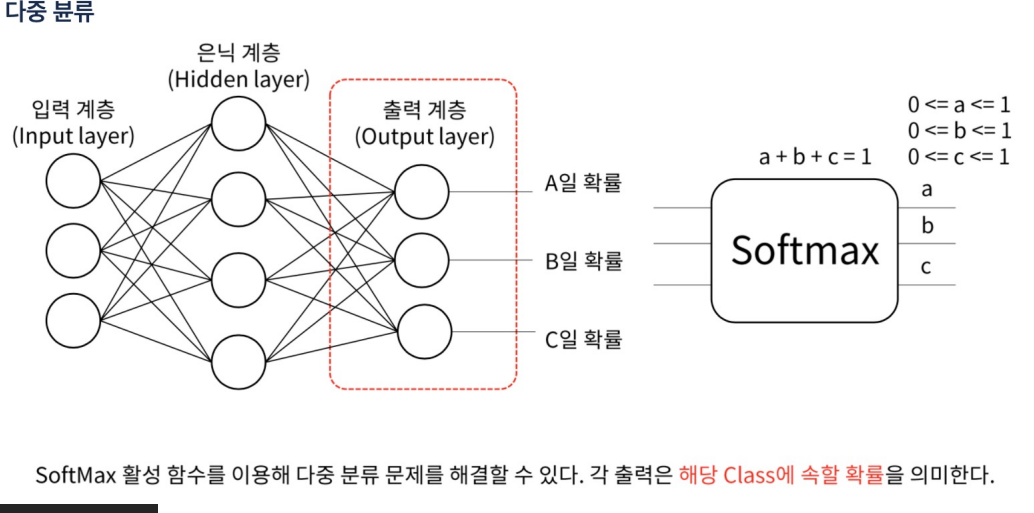
• 회귀 문제에서는 일반적으로 선형 활성화 함수를 사용하고, 분류 문제에서는 softmax 또는 sigmoid 활성화 함수를 사용

• 예측 생성: 출력 계층은 모델의 최종 예측 결과를 생성

• 손실 계산: 출력 계층의 예측과 실제 레이블 간의 차이를 계산하여 손실을 도출

• 이진 분류: 출력 계층에는 하나의 뉴런이 있고, 활성화 함수로는 sigmoid를 사용

• 다중 클래스 분류: 출력 계층에는 클래스의 수만큼 뉴런이 있고, 활성화 함수로는 softmax를 사용

• 회귀: 출력 계층에는 하나의 뉴런이 있고, 활성화 함수로는 선형 함수(또는 아무 함수도 사용하지 않음)를 사용
  
  

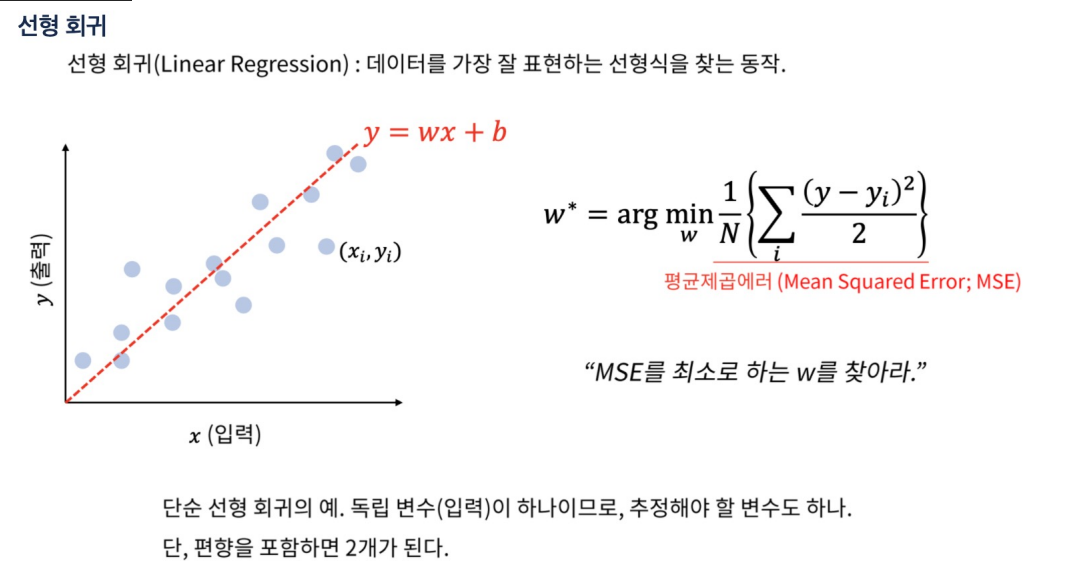
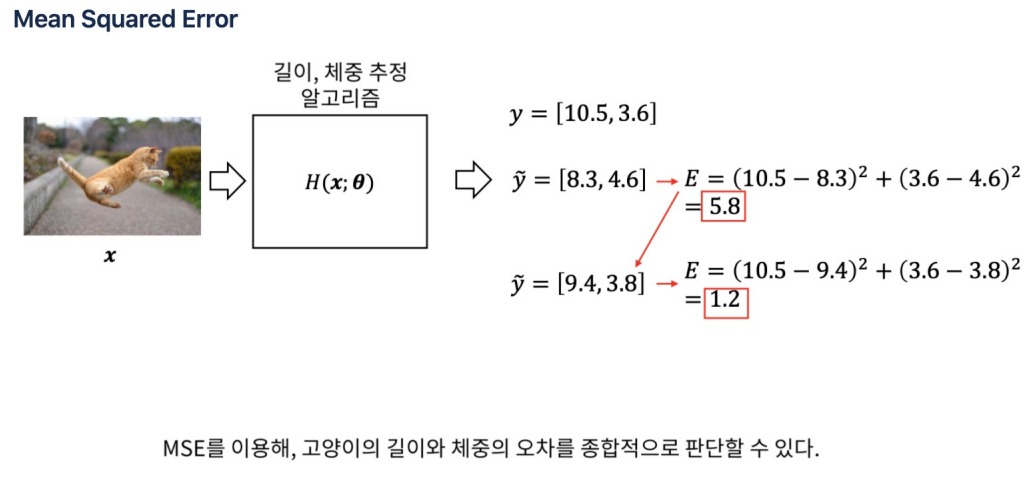
• MSE(Mean Squared Error) :회귀 문제에서 주로 사용되는 손실 함수

• MSE는 모델의 예측값과 실제값의 차이를 제곱하여 평균을 내는 방식으로 계산

• MSE는 모델의 예측 오차를 정량화하는 데 사용되며, 이 값을 최소화하는 것이 모델 학습의 목표

• MSE는 항상 0 이상의 값을 가집니다. MSE가 0에 가까울수록 모델의 예측이 실제값에 가깝다

• MSE는 제곱을 포함하기 때문에, 큰 오차에 대해서는 작은 오차보다 더 큰 벌칙을 부과

• MSE는 미분 가능하므로, 경사 하강법과 같은 최적화 알고리즘을 사용하여 모델의 가중치를 업데이트하는 데 유용
  

• 벡터의 내적(dot product):두 벡터의 상응하는 요소들을 곱한 후 그 결과를 모두 더하는 연산

• 내적은 벡터의 방향과 크기에 대한 정보를 포함하며, 두 벡터 간의 각도를 계산

• 신경망에서 내적은 입력 벡터와 가중치 벡터 간의 선형 결합을 계산하는 데 사용
  
  

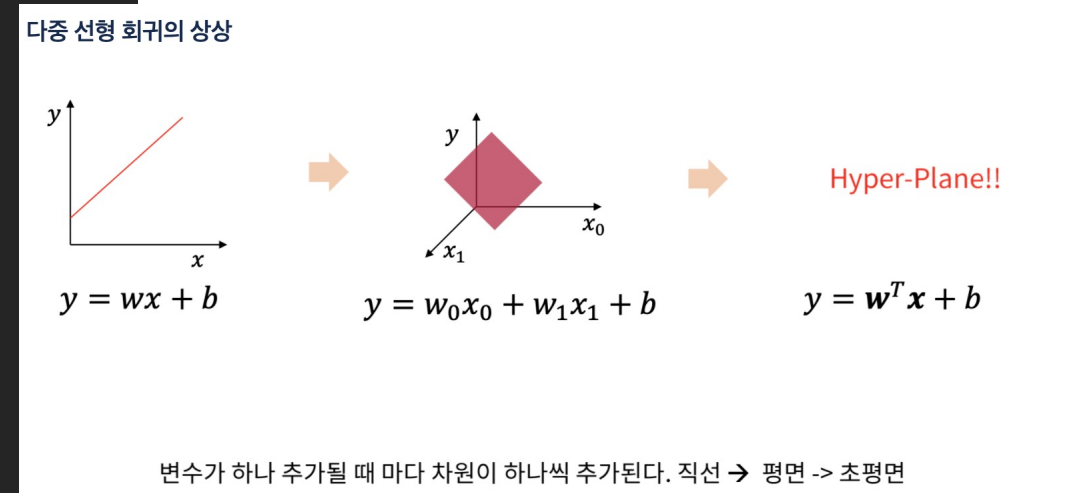
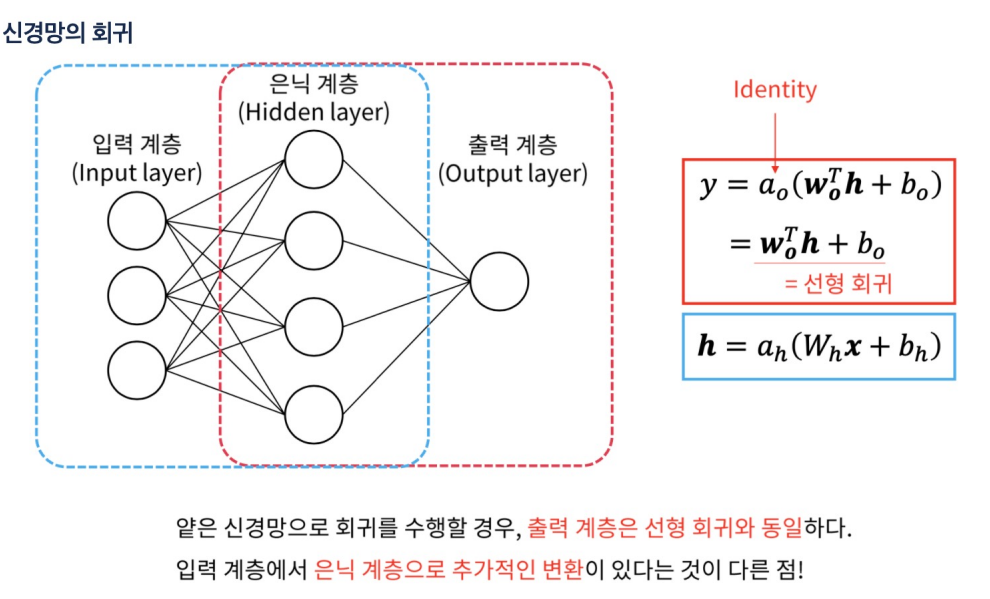
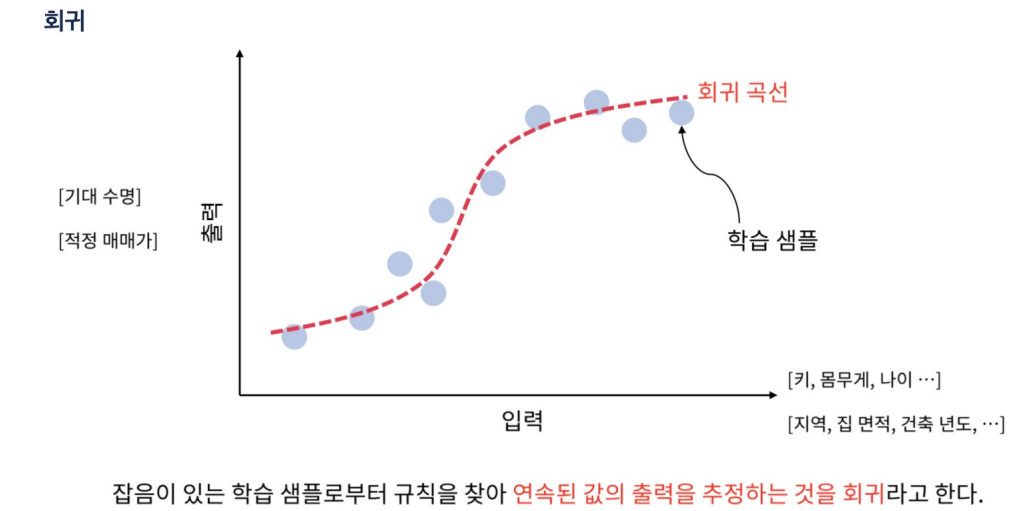
• 얕은 신경망을 사용한 회귀에서는 선형 회귀보다 더 복잡한 패턴을 학습할 수 있는 능력이 있다

• 은닉 계층을 통한 비선형 변환 덕분

• 출력 계층 자체는 선형 회귀와 유사한 선형 변환을 수행합니다.

---

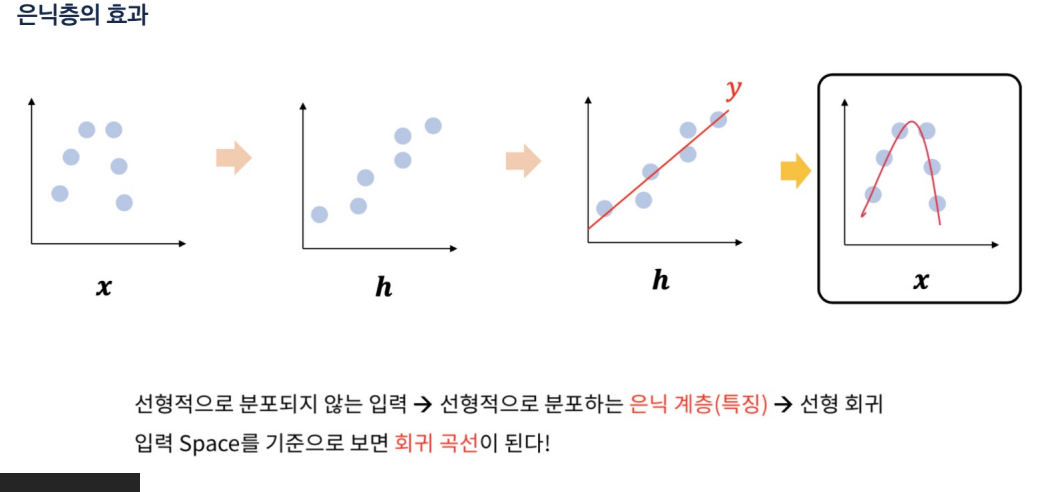
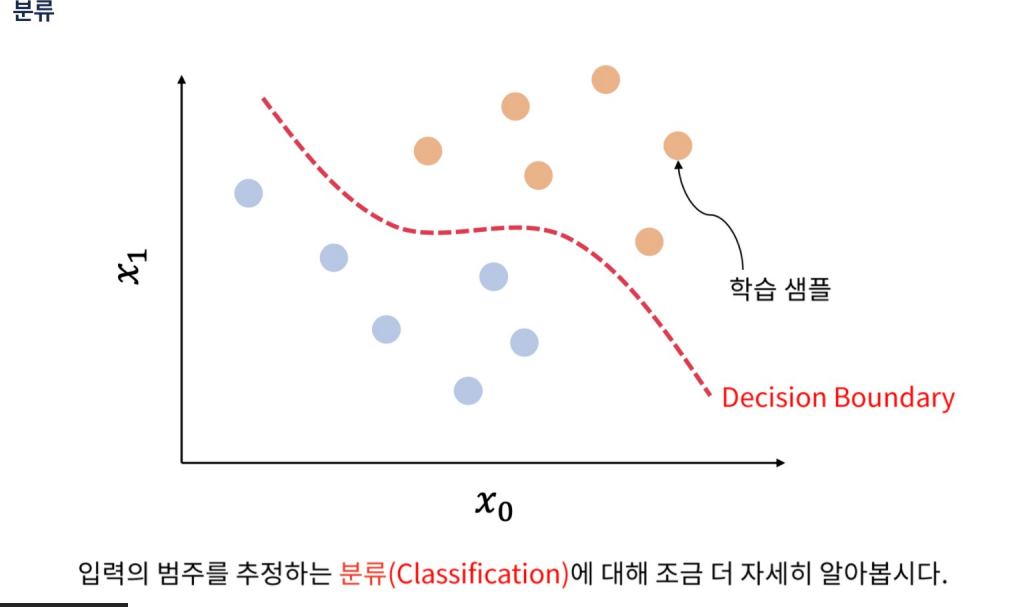
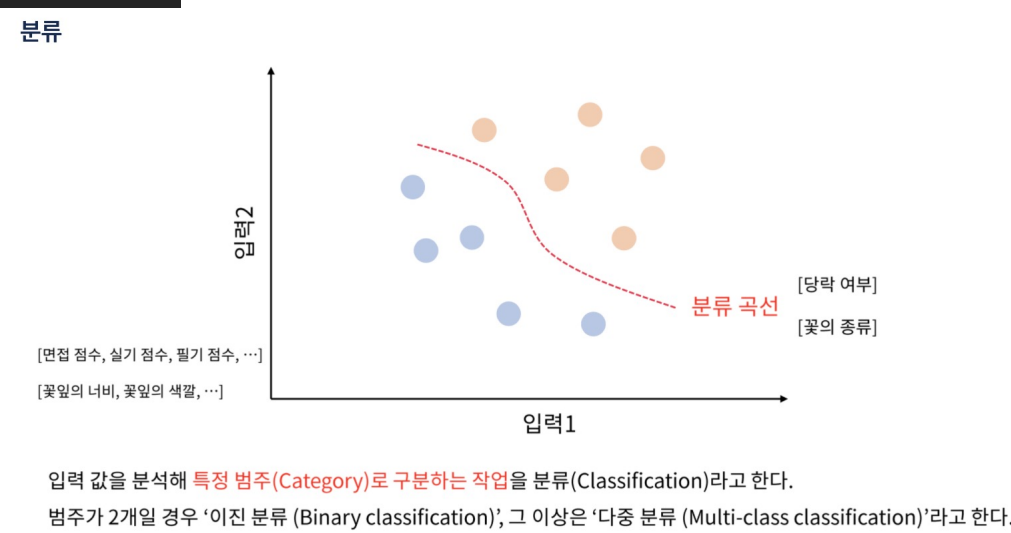
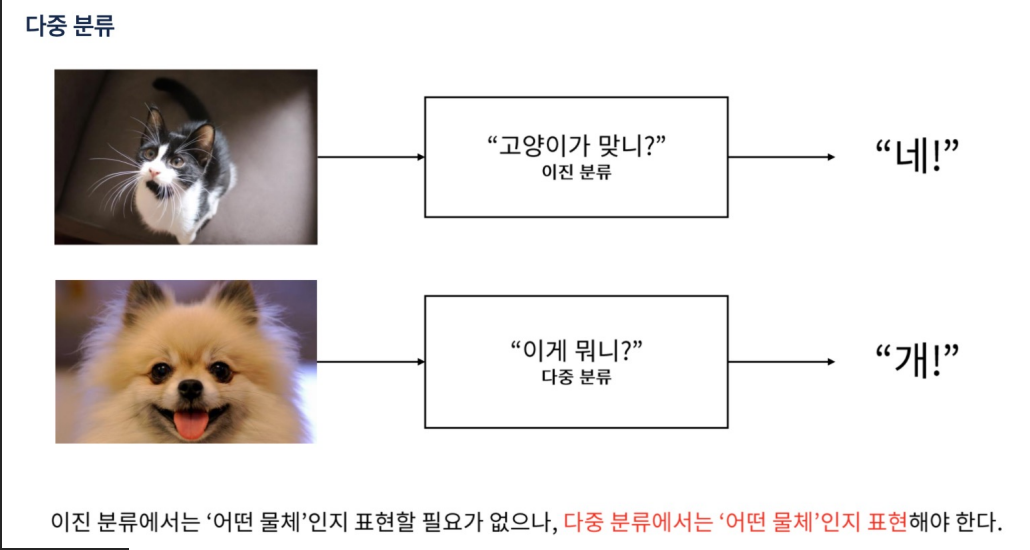
• 범주형? 두 개 이상의 범주(카테고리)로 나눌 수 있는 데이터 유형을 말한다. 이러한 데이터는 수치적이지 않고, 각 범주는 명확하게 구분
• 범주형 데이터는 명목형, 순서형으로 나눈다.
• 명목형 데이터(Nominal Data): 범주 간에 순서나 등급이 없는 경우 (예: 국가 이름, 성별)
• 순서형 데이터(Ordinal Data): 범주 간에 순서나 등급이 있는 경우 (예: 학점 (A, B, C, D, F), 서비스 만족도 (매우 만족, 만족, 보통, 불만족, 매우 불만족))
• 머신러닝 모델은 주로 수치 데이터를 입력으로 받기 때문에, 범주형 데이터를 사용하기 전에 적절한 전처리
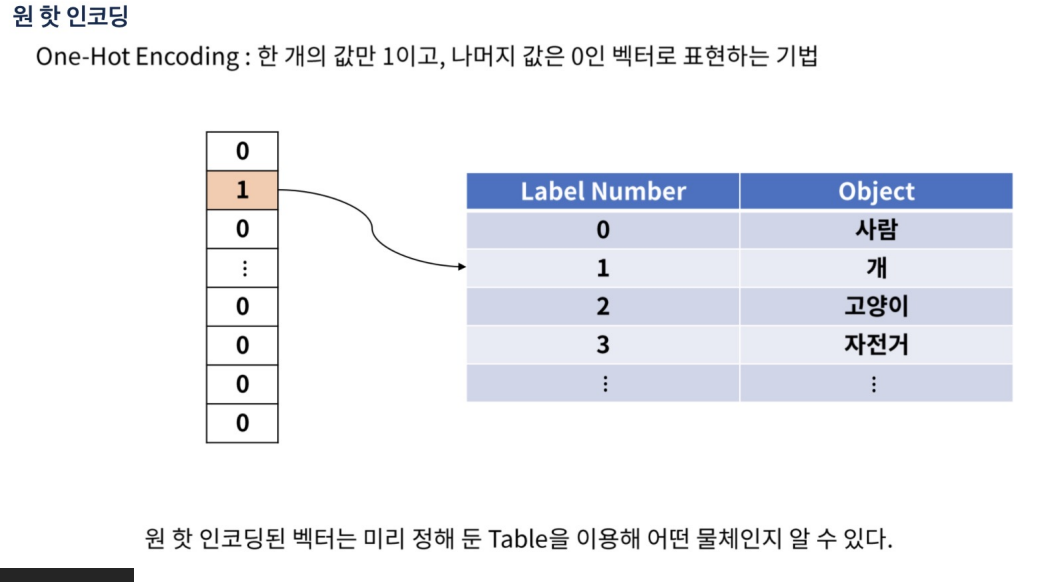
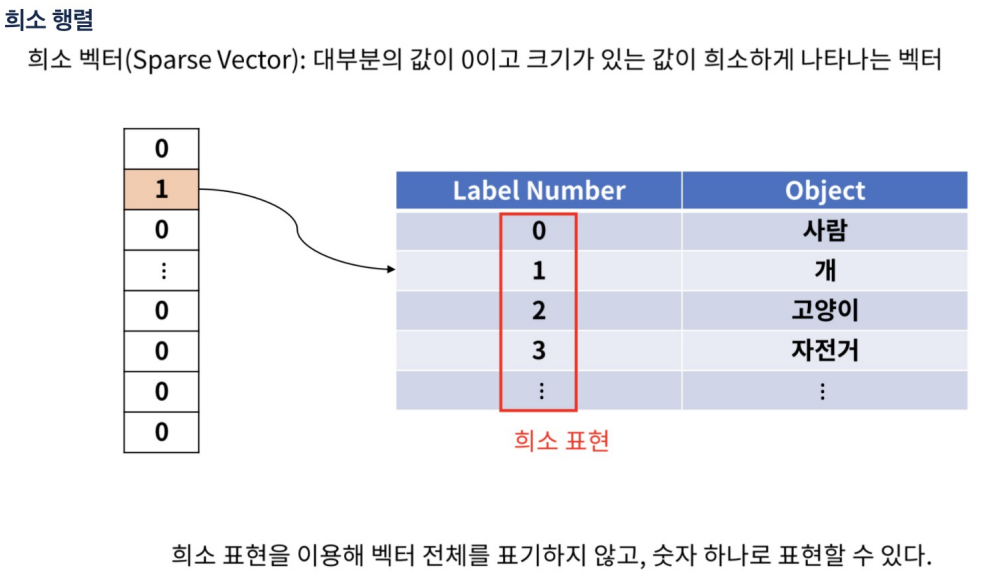
• 처리 방법에는 원-핫 인코딩(One-Hot Encoding), 레이블 인코딩(Label Encoding)
  

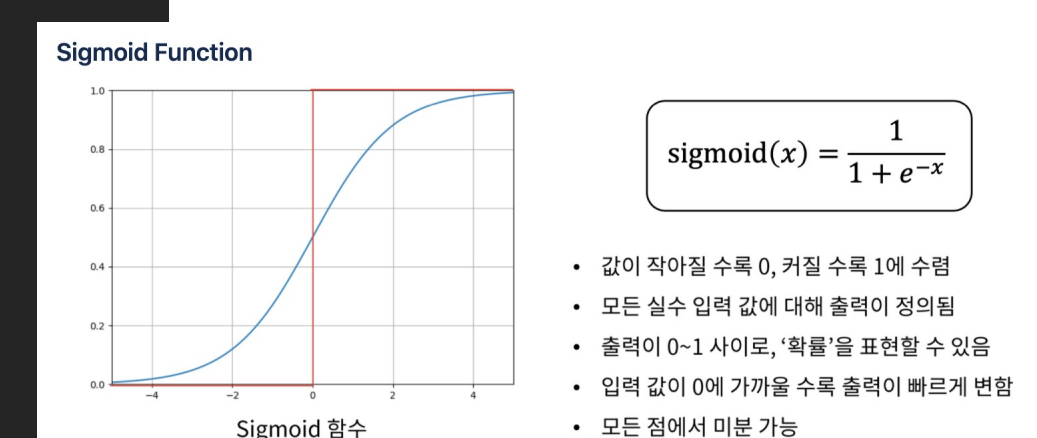
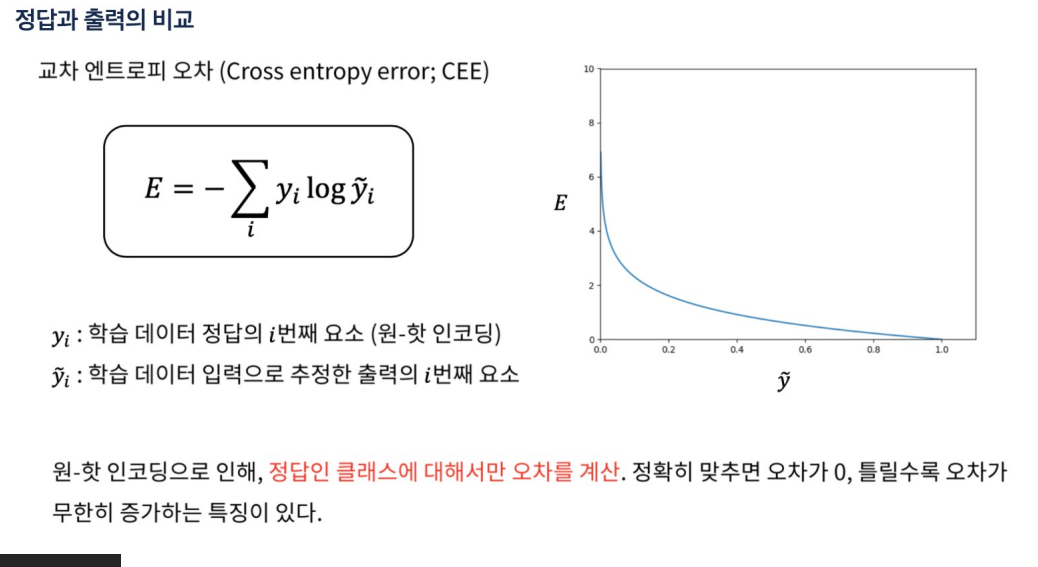
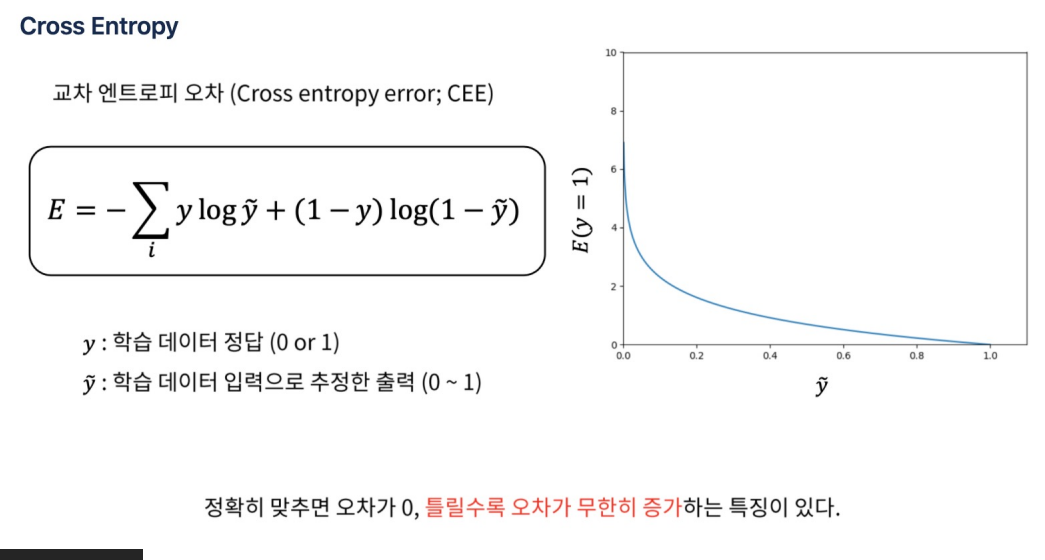
• 손실 함수는 모델의 예측이 실제 레이블과 얼마나 잘 일치하는지를 측정
  
  
  
  
  
  
  
  

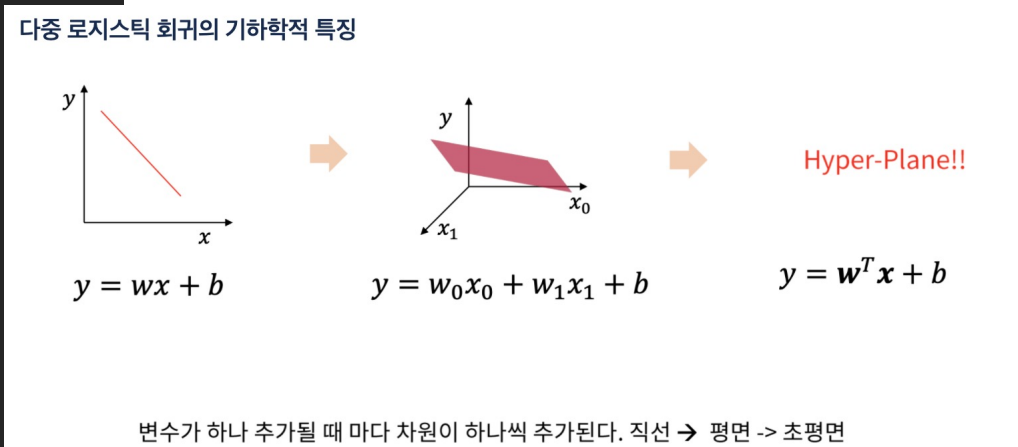
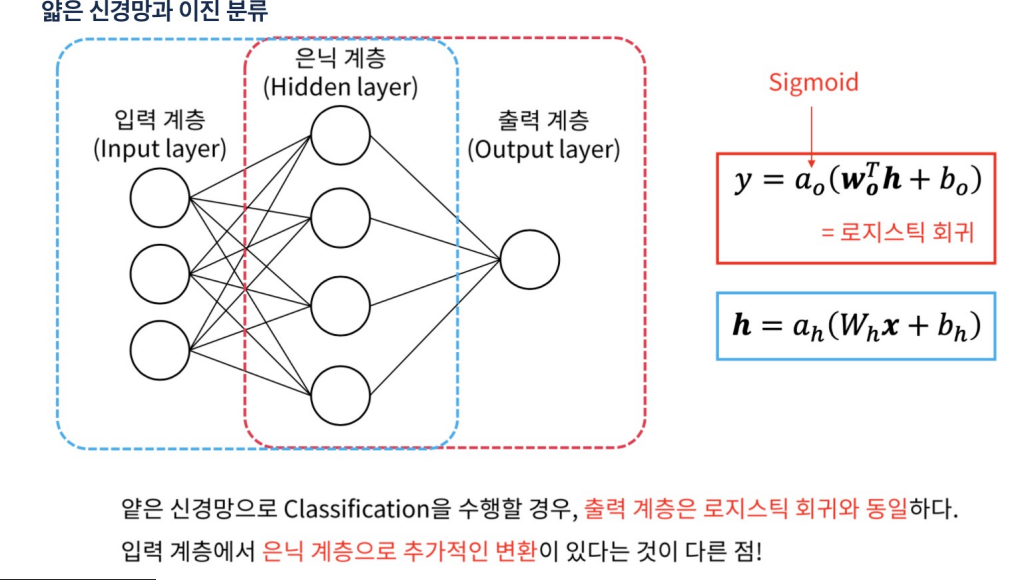
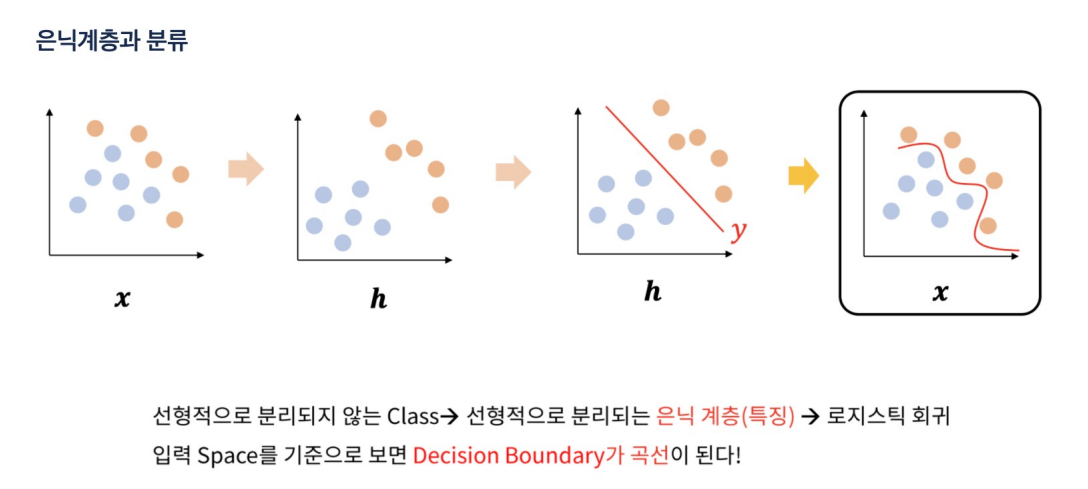
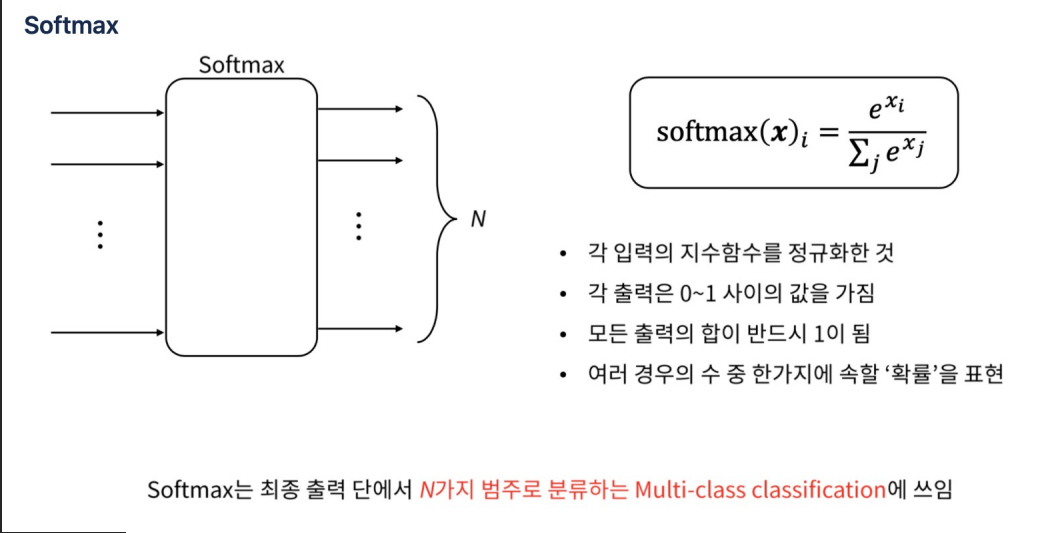
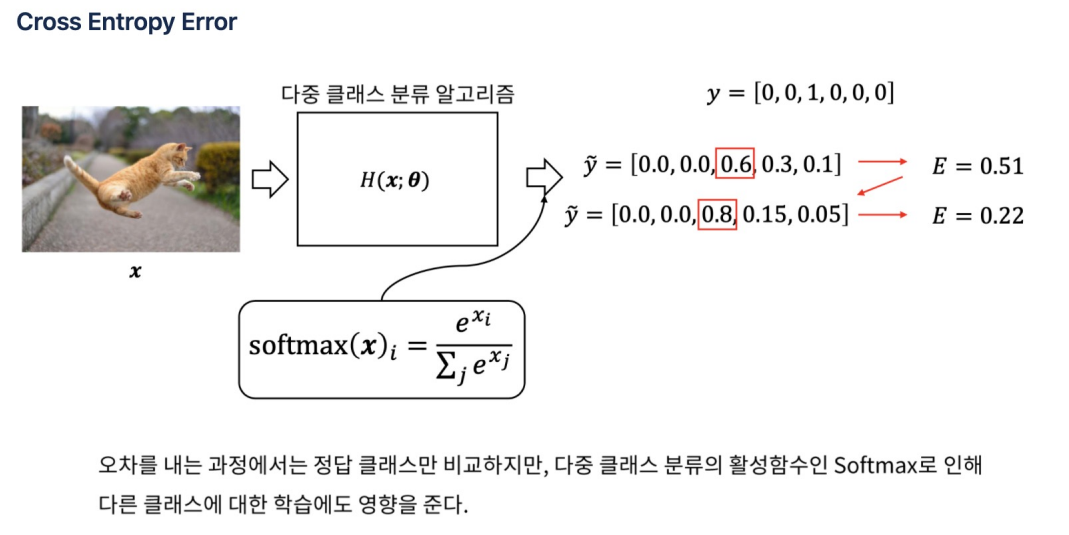
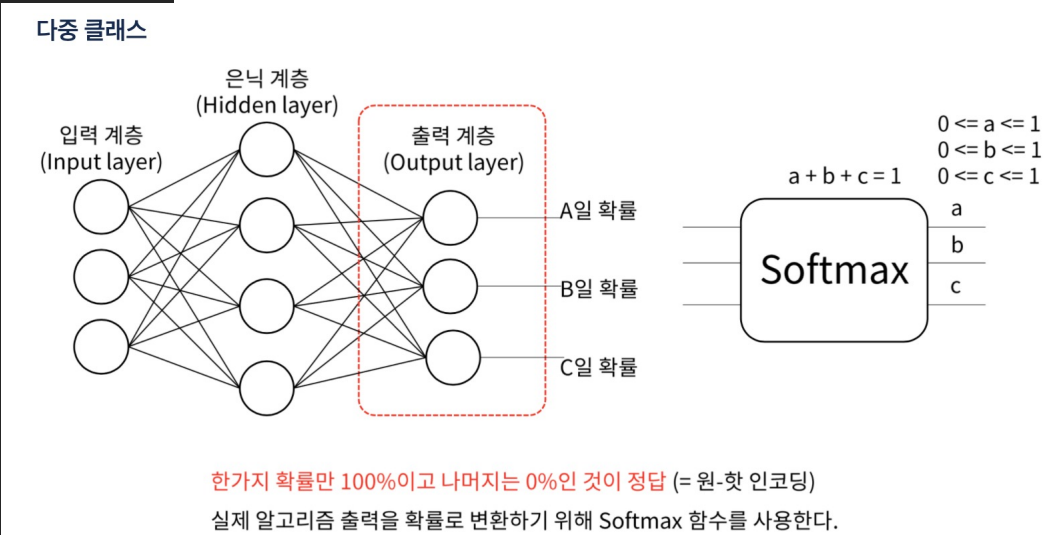
• Softmax다중 클래스 분류 문제에서 사용되는 활성화 함수

• softmax 함수는 신경망의 원시 출력(또는 로짓)을 입력으로 받아, 각 클래스에 대한 확률을 타나내는 값으로 변환한다.

• Softmax 함수는 로짓 벡터의 최댓값에 가장 높은 확률을 할당하며, 다른 값들은 상대적으로 낮은 확률을 할당

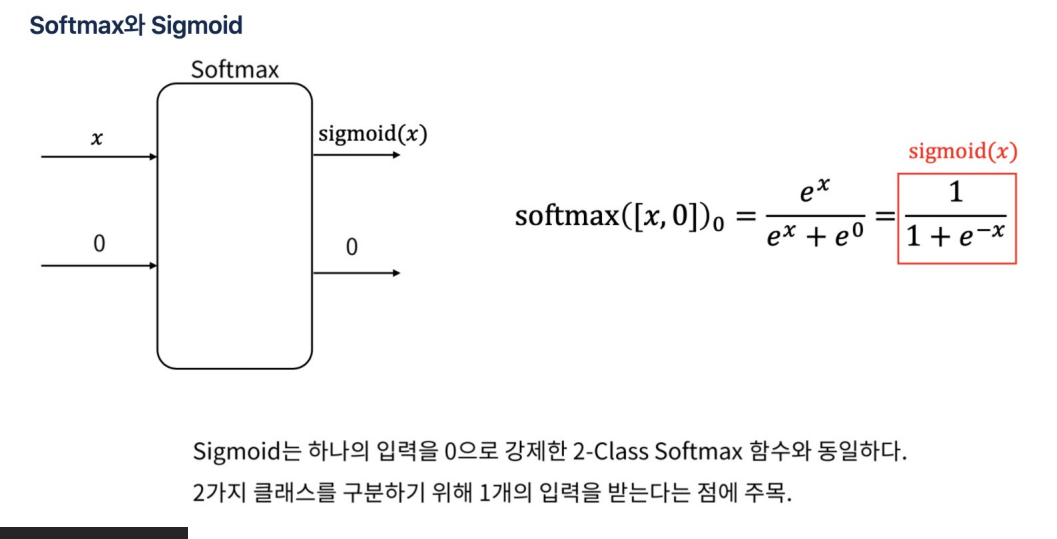
• 두 함수는 모두 하나의 입력을 받아 0과 1 사이의 값을 출력
• 그러나 Sigmoid 함수는 하나의 출력만 생성하는 반면, 2-클래스 Softmax 함수는 두 개의 출력을 생성
• Sigmoid 함수는 출력값이 0.5보다 크면 클래스 1, 작으면 클래스 0으로 분류
• 2-클래스 Softmax 함수는 두 출력 중 더 큰 값을 가진 클래스를 선택
• 요약:두 함수는 수학적으로 동일한 결과를 낼 수 있지만, 구현과 출력 방식에서 차이