Normalization
- 정규화
IMG_SIZE = 180
resize_and_rescale = tf.keras.Sequential([
layers.Resizing(IMG_SIZE, IMG_SIZE),
layers.Rescaling(1./255)])- '정규화'라고 번역이 되는데 Regularization, Standardzation과 차이가 무엇일까?
- Normalization : 값 범위를 왜곡시키지 않고 데이터셋을 공통 스케일로 변경하는 것.
ex. KNN, K-means 등 distance based algorithms을 사용할 때 입력 데이터의 범위를 한정 시키는 것. Min-max scaling 등
- Z-score normalizatioin : 편차가 크면 over fitting 문제가 생기기 때문에, 모델 자체가 잘 안 만들어지는 것을 잘 만들어지게 만듦 - Regularization : 모델의 설명도를 유지하면서 모델의 복잡도를 줄이는 방식
ex. Ealry stopping, Noisy input, Drop out, Pruning&feature selection, Ensemble, L1&L2
-
Gradient Descent Based Algorithms에서는 왜 Normalization을 하는 가?
Gradient descent based algorithms은 최소 loss 값을 찾아가는 것
gradient의 learning rate가 왔다갔다하는 복잡한 현상이 생겨서 최소 loss를 찾아가지 못하는 현상이 발생함
Normalization을 범위를 한정시키기 때문에 floating point issue 방지에도 도움이 됨 -> numerical state를 확보하는 결과가 생김 -
가중치의 초기화
가중치를 동일한 상수로 초기화하게 되면 항상 같은 값이 나오기 때문에 Symmetry problem이 발생함. 하지만 random한 값으로 가중치를 초기화게 되면 symmetry problem은 발생하지 않지만, 값들이 random하게 나옴
따라서, 가중치를 random으로 초기화를 하되, 범위를 제약시키는 방법으로 제약을 두는 방식으로 진행함
=> 평균이 0이고 표준편차가 1인 정규분포에서 가중치를 랜덤하게 초기화하는 방법이 일반적
Batch Normalization
AlexNet에서는 Local Response Normalization(LRN)을 사용하였으나, Layer가 깊어짐에 따라 좋지 못한 성능을 보이는 것을 밝혀냄
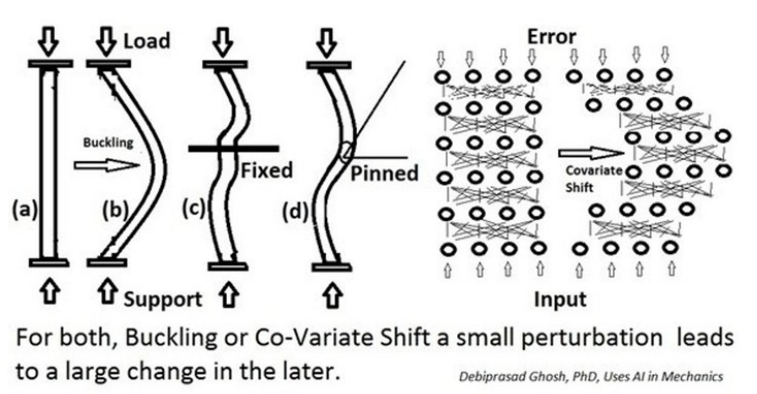
Batch Normalization
Normalization이 안 되면 값이 전혀 관계가 없는 분포로 바뀌어 버리는 Internal covariance shift 문제가 발생하는 것을 방지하기 위해 Batch Normalization을 고안함.
그러나 2017년도 후속 논문에선 Internal covariance shift를 Batch Normalization을 통해 해결은 못하지만 효과가 아주 좋다는 후속 논문이 나왔음
Whitening 방법
- input의 feature들을 uncorrelated 하게 만들어 주고, 각각의 variance를 1로 만들어 주는 기법(standardzation)
- 문제점 : 모든 데이터를 계산하고, 평균을 0, 표준편차를 1로 만들어야 하는 것은 거의 불가능함
=> 학습할 때 Batch 단위로 whitening을 하여 계산 복잡도를 줄어들이자!
Batch Normalization 사용 방법

- mini-batch mean
- 'samling한 평균은 전체 평균과 같아진다'는 특징을 활용하여 학습할 때 batch 단위로 whitening을 진행한다
- normalize
- whitening할 때 분모의 값이 0이 되는 것을 방지하여 아주 작은 값인 epslion을 더한다 (numerical stability를 보장하기 위해)
- scale and shift
- scale and shift연산을 한다 (learned parameter γ,β를 추가한다)
- 데이터가 지나가면서 internal covariance shift 문제가 발생하지 않도록, 학습을 통해 찾아내서 non-linearity를 유지하도록 한다
- BN은 activation layer이전에 위치하는데 normalization을 한 후에 activation layer를 통과하게 되면 non-linearity를 감소시킬 우려가 있다
