Introduction

랜덤 포레스트(Random Forest)를 학습한 후, 많은 변수 중 가장 예측력이 강한 변수가 무엇인지 파악하기 위해 변수 중요도(Variable Importance)를 확인한 경험이 있으실 겁니다. 이번 포스팅에서는 랜덤 포레스트에서 변수 중요도를 계산하는 방법 3가지에 대해 소개하도록 하겠습니다.

1. MDI(Mean Decrease in Impurity) Importance
2. Permutation Importance
3. Drop column Importnace

랜덤 포레스트(Random Forest)

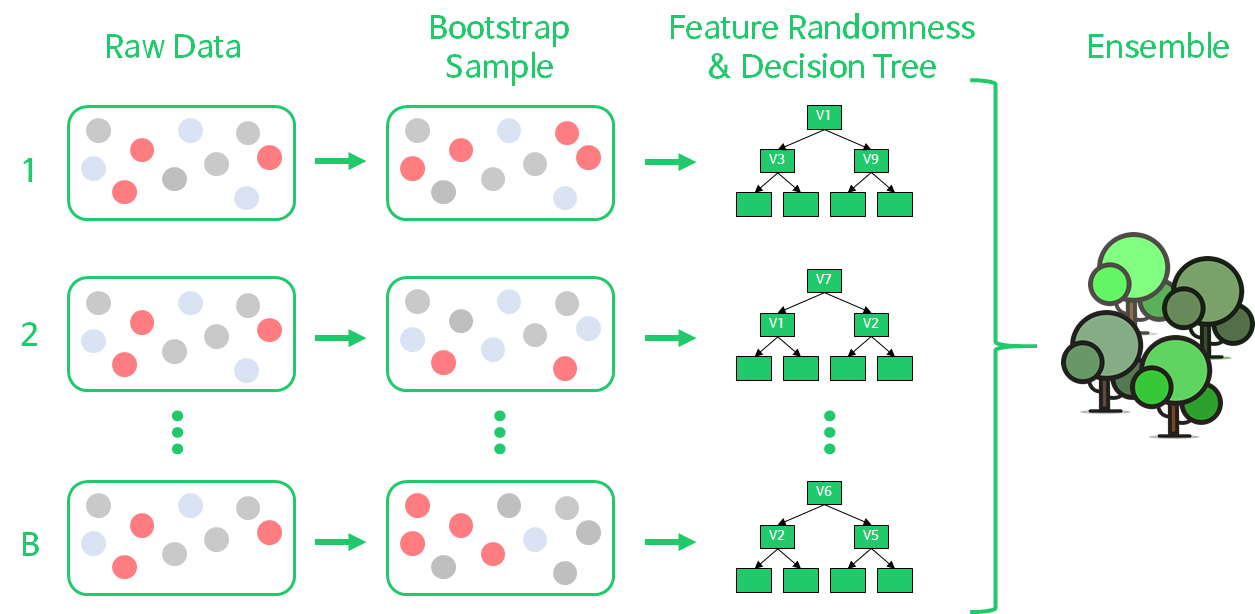
랜덤 포레스트란, 의사결정나무의 과적합(Over Fitting)을 해결하기 위해 여러개의 의사결정트리를 취합하여 학습성능을 높이는 앙상블 모형(Ensemble Model)입니다.

랜덤 포레스트는 아래와 같이 구현됩니다.

1. Bootstrap Sampling : 전체 데이터 N개에서 N개의 sample을 복원추출
2. Feature Random Selection : 의사결정나무를 분개할 때마다 변수 중 p개를 선택하여, 최적의 변수와 split-point를 선정
3. 1~2번 단계를 B번 반복하여, 결과를 취합

랜덤 포레스트는 각 나무에서 데이터와 변수 모두 랜덤으로 선택하기 때문에, 각 나무가 uncorrelated model(≒ 독립적)로 다양하고 풍부한 표현력을 갖는 강점이 있습니다.

변수 중요도(Variable Importnace)

랜덤 포레스트가 많은 강점이 있음에도 불구하고, 블랙박스모형이기 때문에 설명변수와 반응변수의 설명력을 확보하기 어렵다는 단점도 있습니다.
이를 어느 정도 해결하기 위해, 변수 중요도(Variable Importance)라는 척도를 통해 어느 변수가 예측 성능에 중요한 역할을 하는지를 추정하곤 합니다.

블랙박스모형에서 설명변수와 반응변수의 관계 살펴보기 - Partial Dependence Plot (PDP) 맛보기

변수 중요도는 "해당 변수가 상대적으로 얼마만큼 종속변수에 영향을 주는가?"에 대한 척도이기 때문에, "어떻게 영향을 주는가?"에 대한 답변으로는 적절하지 않습니다.
Partial Dependece Plot은 블랙박스모형에서 설명변수가 종속변수에게 주는 marginal effect를 추정하는 방법입니다.

1. MDI(Mean Decrease in Impurity) Importance

MDI Importance는 가장 대표적인 변수 중요도로서, scikit-learn의 default로 내장되어 있는 방법론입니다.
각 변수가 split될 때 impurity 감소분의 평균을 중요도로 정의하는 것으로 식은 아래와 같습니다.

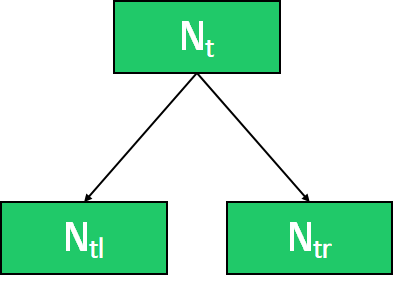
• $i(t)$ : t노드의 impurity (entropy, gini index, variance, ...)
• $N_{t}$ : t노드의 관측치 개수

각 노드의 관측치 개수를 고려하여 impurity 감소분이 계산되며, 값이 클수록 중요도가 높습니다.

• 장점 : 빠르고, 직관적임
• 단점 : 연속형 변수와 high-cardinality 범주형 변수에 대해서는 편향됨.

“the variable importance measures of Breiman's original Random Forest method ... are not reliable in situations where potential predictor variables vary in their scale of measurement or their number of categories.” (Bias in random forest variable importance measures: Illustrations, sources and a solution)

2. Permutation Importance

Permutation Importance는 "해당 변수가 랜덤으로 분포된다면, 어느 정도 성능이 떨어지는가?"라는 가정을 갖고 있습니다. Permutation Importance는 랜덤포레스트의 각 나무에서 OOB(Out of Bag) sample에서 다음과 같이 구현됩니다.

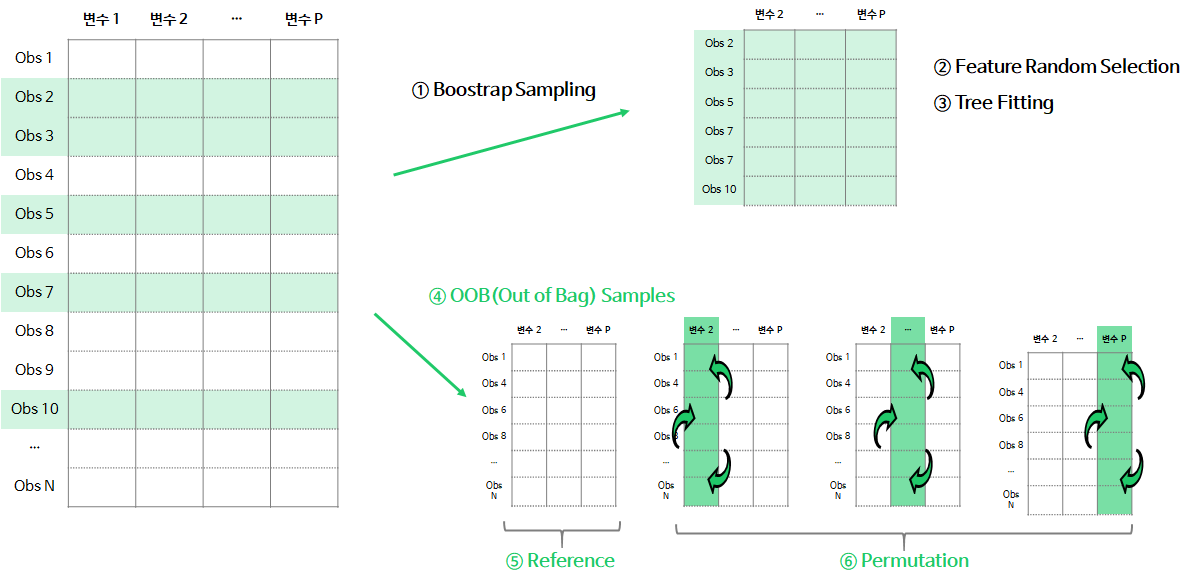
1. (①~③) b번째 tree를 생성할 때, bootstrap sample로 나무를 학습
2. (④) OOB Samples : 학습할 때 사용되지 않은 데이터 셋으로 Validation 데이터를 생성
3. (⑤) Reference Measure : OOB Sample로 나무의 예측력(accuracy, R-square, MSE 등)을 계산 및 저장
4. (⑥) Permutation Measure : OOB Sample에서 j번째 변수의 데이터를 무작위로 섞은 뒤, 학습된 나무의 예측력을 계산 및 저장
5. ⑤, ⑥단계에서 저장된 예측력 척도의 차이(Reference Measure - j번째 변수의 Permutation Measure)를 계산

위의 과정을 나무의 개수 B만큼 시행하여, 각 변수에서 계산된 중요도의 평균으로 Permutation Importance로 정의합니다.

위의 과정 중 특정 변수를 무작위로 섞었을 때 기존 Reference 척도보다 낮아지게되면, 해당 변수는 중요하다고 판단되며 척도가 유사하거나 오히려 좋아지면 불필요하다고 판단내릴 수 있습니다.

• 장점 : 모델을 다시 학습하지 않아도 되기 때문에, 계산이 빠름. 직관적임.
• 단점 : Permutation importance overestimates the importance of correlated predictors — Strobl et al (2008)

OOB(Out of Bag) Sample

N개의 데이터에서 Boostrap Sampling으로 N개의 데이터를 선택하고, 선택되지 못한 데이터를 OOB Sample이라고 합니다. OOB Sample은 학습에 사용되지 않았기 때문에, validation 용도로 사용할 수 있다는 장점이 있습니다.

- 관측치 A가 OOB Sample에 포함될 확률
: 복원추출을 한 번 시행할 때, 데이터 N개 중 관측치 A가 뽑히지 않을 확률은 $\frac{N-1}{N}$ 입니다. 이 과정을 충분히 큰 N번 반복하면 다음과 같은 확률이 계산됩니다.

$\lim_{N\rightarrow\infty}(\frac{N-1}{N})^{N} = \lim_{N\rightarrow\infty}(1-\frac{1}{N})^N = e^{-1} = 0.368$

3. Drop Column Importance

Drop Column Importance 방법은 모든 변수를 사용했을 때의 Reference척도에서 특정 변수를 빼고 랜덤포레스트를 다시 학습했을 때의 척도의 차이로 변수 중요도를 정의합니다.
Permutation Importance와 동일하게, 변수를 뺏을 때의 성능이 많이 떨어진다면 해당 변수는 중요한 변수라고 할 수 있습니다.

• 장점 : 개념이 매우 직관적임
• 단점 : 변수의 개수만큼 모델 재학습이 필요하기 때문에, Computation 관점으로 매우 비효율적

Reference

• Eryk Lewinson 블로그
• explained.ai
• 사쿠의 데이터 블로그