Introduction

머신러닝을 시작하면, 가장 먼저 볼 수 있는 것이 아마 선형회귀분석(Linear Regerssion Analysis)일 것입니다.

Q. 선형회귀분석의 '선형'의 의미는 무엇일까요?

'선형(Linear)'의 의미를 '독립변수와 종속변수의 관계 그래프가 직선인 경우'라고 생각하신다면, 잘못된 생각입니다.

이번 포스팅에서는 일반선형회귀와 일반화선형회귀를 비교하면서 "선형"과 "일반화"의 의미에 대해 소개하려고 합니다.

회귀분석(Regression Analysis)이란?

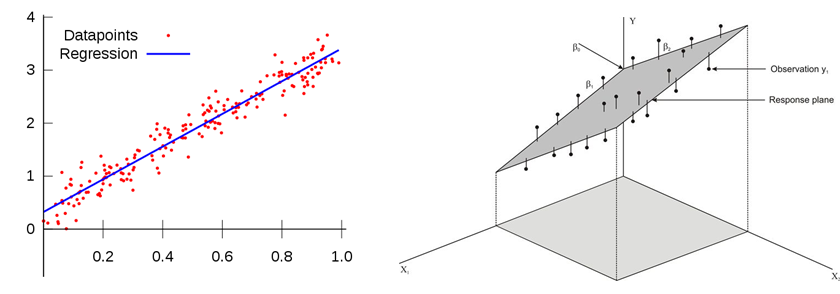
회귀분석은 여러 개의 독립변수와 하나의 종속변수 간의 상관관계를 모델링하는 기법을 통칭합니다.
즉, X인자를 통해 Y를 설명하고자 하는 넓은 영역을 말합니다.

일반화선형회귀 - 일반화, 선형의 의미

1. 선형회귀(Linear Regression)이란?

선형회귀의 정확한 정의는 종속변수의 평균이 독립변수와 회귀계수(Regressin Coefficient)들의 선형결합(Linear Combination)으로 된 회귀모형을 말하며, 회귀계수를 선형 결합으로 표현할 수 있는 모형을 뜻합니다.

다음의 두 예제가 대표적인 선형회귀입니다.

1. $y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2}$
2. $y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2}^2$ → ($x_{2}^2$을 $x_{3}$로 치환) $y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{3}$

특히, 2번의 경우 $x_{2}$에 대한 제곱항이 있지만, $x_{3}$으로 치환하면 1번과 같은 식으로 나타낼 수 있습니다.
여기서 꼭 주의하셔야 할 점은 "선형의 의미가 독립변수와 종속변수가 꼭 직선의 그래프 형태(1차식)를 나타내는 것이 아니다."라는 점 입니다.

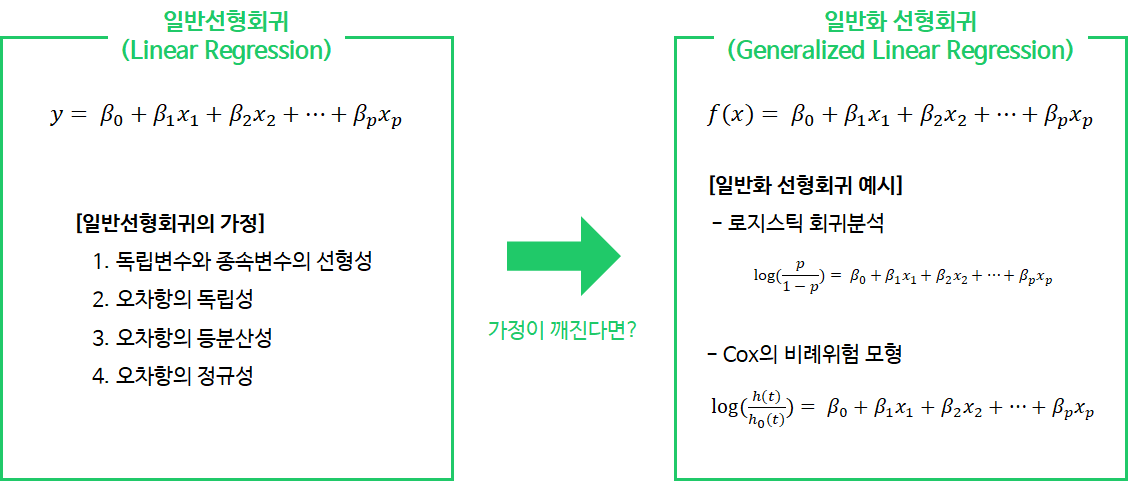
2. 일반화선형회귀(Generalized Linear Regression, GLM)이란?

일반선형회귀의 경우 선형성, 독립성, 등분산성, 정규성의 가정을 갖고 있습니다. 하지만, 종속변수가 연속형이 아니라면 대표적으로 오차항의 정규성 가정이 깨지게 됩니다.
대표적으로 로지스틱 회귀(Logistic Regression)과 Cox의 비례위험회귀(Cox's Proportional Hazard Regression)는 대표적인 일반화선형회귀이며, 일반화선형회귀는 종속변수를 적절한 함수로 변화시킨 $f(y)$를 독립변수와 회귀계수의 선형결합으로 모형화한 것입니다.

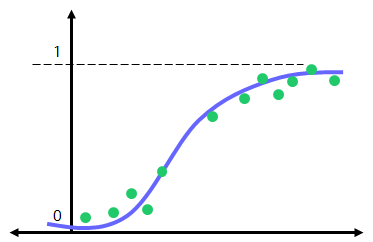
로지스틱 회귀(Ligistic Regression)

로지스틱 회귀는 종속변수가 이분형(ex. 실패/성공, 0/1, 생존/사망…)일 때의 일반화선형회귀 중 하나로서, log odds($log(\frac{y}{1-y}$)에 대해 독립변수와 회귀계수의 선형결합으로 모형화합니다.

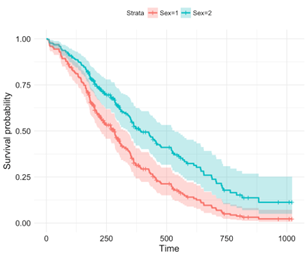
Cox의 비례위험회귀(Cox's Proportional Hazard Regression)

Cox의 비례위험회귀는 시간에 따라 hazard ratio($log(\frac{h(t)}{h_0(t)})$)가 일정하다는 가정을 갖은 생존분석 중 가장 많이 쓰이는 방법론으로서, 어떤 사건(event)이 일어날 때까지의 시간을 대상으로 분석하는 통계방법입니다.

Summing Up

• 선형(Linear) 모형 : 회귀계수를 독립변수의 선형결합으로 나타낸 모형
• 일반화선형회귀 : 종속변수를 변환하여, 회귀계수를 독립변수의 선형결합으로 나타낸 모형

Reference

• Statistics by Jim
• gimmesilver님 블로그
• 높이 비상하는 즐거운 상상