Abstract

• 문제 정의: 컴퓨터 비전에서 이미지에 대한 고품질의 세그멘테이션 마스크를 생성하는 것은 중요한 문제입니다. 특히, 대규모 주석(annotation) 없이 모든 종류의 이미지에 대해 제로 샷(zero-shot, 학습 시 보지 못한 데이터에 대해 추론하는 능력) 세그멘테이션을 달성하는 것은 여전히 어렵습니다. 기존 연구들 (SAM 등)은 대규모 지도 학습을 통해 제로 샷 능력을 얻었지만, 주석 수집 비용이 높습니다. 반면, 비지도 학습(unsupervised training)은 주석이 필요 없지만, 일반적으로 특정 데이터셋에 대한 적응이 필요하거나 추가 정보를 요구하는 제약이 있었습니다.
• 제안 방법 (DiffSeg): 사전 학습된 Stable Diffusion 모델(High-Resolution Image Synthesis with Latent Diffusion Models 등)의 self-attention 레이어에 객체 그룹화에 대한 내재적인 정보가 학습되어 있다는 가설을 기반으로 합니다. 이 가설을 활용하여, DiffSeg는 self-attention 맵을 세그멘테이션 마스크로 변환하는 간단하면서도 효과적인 후처리 방법을 제안합니다.
• 핵심 기술: DiffSeg는 attention 맵 간의 유사성을 측정하는 KL divergence를 사용하여 attention 맵을 유효한 세그멘테이션 마스크로 반복적으로 병합하는 과정을 거칩니다. 이 과정은 'Iterative Attention Merging'이라고 불립니다.
• 주요 특징:
  • 비지도 학습 및 제로 샷: 어떠한 학습이나 주석 없이 작동합니다.
  • 언어 독립적: 텍스트 프롬프트(Diffumask: Synthesizing Images with Pixel-Level Annotations for Semantic Segmentation Using Diffusion Models)와 같은 언어 정보에 의존하지 않습니다.
  • 모든 이미지 세그멘테이션: 사전 지식 없이 어떤 이미지든 세그멘테이션할 수 있습니다.
• 성능: COCO-Stuff-27 데이터셋에서 기존 비지도 제로 샷 SOTA 방법(ReCo) 대비 픽셀 정확도(pixel accuracy)에서 절대 26%, 평균 IoU(mean IoU)에서 17% 성능 향상을 달성했습니다.

1. Introduction

• Semantic Segmentation의 중요성과 Zero-Shot Transfer의 도전 과제

  • 이미지의 segmentation mask를 생성하는 것은 컴퓨터 비전의 기본적인 문제입니다. 이는 이미지 편집, 의료 영상, 자율 주행 등 다양한 분야의 핵심 기술입니다. 지도 학습 기반 semantic segmentation은 잘 연구되었지만, 어떤 이미지든 알려지지 않은 카테고리에 대해 segmentation하는 zero-shot transfer segmentation은 훨씬 어렵습니다.
  • 최근 SAM과 같은 연구는 11억 개 이상의 annotation으로 학습하여 zero-shot transfer에서 인상적인 성능을 보였지만, 이는 특정 데이터셋에 국한되지 않고 segmentation을 더 유연한 기본 작업으로 만드는 중요한 진전입니다.

• 비지도 Zero-Shot Segmentation의 어려움 및 기존 연구의 한계

  • 그러나 per-pixel 라벨 수집 비용은 매우 높습니다. 따라서 annotation이나 대상에 대한 사전 지식 없이 비지도 및 zero-shot transfer segmentation 방법을 연구하는 것이 중요합니다. 비지도 및 zero-shot 요구 사항을 동시에 만족하는 것은 어려워 몇몇 연구만이 이 문제에 도전했습니다.
  • 대부분의 비지도 segmentation 연구는 대상 데이터에 대한 비지도 adaptation을 요구하거나, ReCo처럼 미리 개념을 식별하고 대규모 이미지 풀을 유지해야 하는 등 SAM의 능력에는 미치지 못하는 제약이 있습니다.

• Stable Diffusion 모델의 활용 가능성 탐색

  • 이러한 목표를 향해 나아가기 위해, 본 논문은 일반적인 segmentation 모델을 구축하기 위해 Stable Diffusion (SD) 모델의 능력을 활용할 것을 제안합니다. Stable Diffusion 모델은 최근 프롬프트 조건부 고해상도 이미지 생성에 사용되었습니다. 확산 모델 내부에 객체 그룹화에 대한 정보가 존재할 것이라고 가정하는 것은 합리적입니다.
  • 예를 들어, DiffuMask는 cross-attention 레이어가 생성된 attention 맵과 입력 프롬프트를 상호 참조할 때 명시적인 객체 수준 픽셀 그룹화를 포함함을 발견했지만, 이는 프롬프트에 의해 명시적으로 언급된 지배적인 전경 객체에만 적용되며 생성된 이미지에 대해서만 segmentation mask를 생성할 수 있다는 한계가 있습니다.

• Self-Attention 레이어의 객체 그룹화 특성 분석

  • 이러한 동기 부여를 바탕으로, 본 논문은 확산 모델의 unconditioned self-attention 레이어를 조사합니다. Self-attention 레이어의 attention tensor가 특정 공간적 관계인 Intra-Attention Similarity와 Inter-Attention Similarity (3.1절)를 포함하고 있음을 관찰했습니다. 이 두 가지 속성에 의존하여 이미지 내 어떤 객체에 대해서도 segmentation mask를 발견하는 것이 가능합니다.
  • 다양한 해상도의 attention 맵은 원본 이미지에 대해 다른 크기의 receptive field를 가지며, 저해상도 맵(예: 8x8)은 전체적인 대형 객체 그룹화에 효과적이고, 고해상도 맵(예: 16x16)은 대형 객체의 구성 요소에 대한 더 세밀한 그룹화나 작은 객체 식별에 더 좋습니다. 현재 Stable Diffusion 모델은 4가지 해상도의 attention 맵을 가집니다.

• 제안하는 방법론 DiffSeg 소개 및 성능 요약

  • 이러한 관찰을 바탕으로, 본 논문은 DiffSeg (3.2절)를 제안합니다. 이는 확산 모델의 self-attention 레이어에서 생성된 attention tensor만을 사용하여 segmentation mask를 생성하는 간단하면서도 효과적인 후처리 방법입니다.

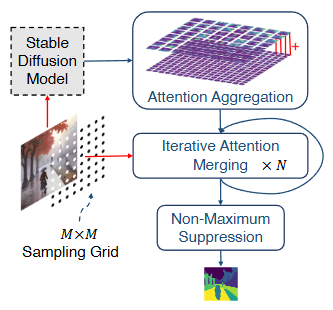
  • 이 알고리즘은 주의력 집계(attention aggregation), 반복적 주의력 병합(iterative attention merging), 비최대 억제(non-maximum suppression)의 세 가지 주요 구성 요소로 이루어집니다(그림 1).

  • DiffSeg는 기존의 비지도 segmentation 방법들과 달리 클러스터 수를 미리 지정할 필요가 없으며 결정론적입니다. 어떤 이미지든 사전 지식 없이, DiffSeg는 추가 리소스에 의존하지 않고 고품질의 segmentation을 생성할 수 있습니다. COCO-Stuff-27 및 Cityscapes 벤치마크에서 이전 연구들을 능가하는 최신 성능을 달성했습니다.

파이프라인

그림1

• Stable Diffusion Model: 먼저 입력 이미지가 미리 학습된 Stable Diffusion 모델에 주입됩니다. 이 모델은 일반적으로 이미지를 생성하는 데 사용되지만, DiffSeg는 생성 기능 자체보다는 모델 내의 자기 어텐션 레이어에서 생성되는 어텐션 텐서(attention tensor)를 추출하여 활용합니다. 논문에서는 이 어텐션 레이어들이 이미지 내 객체 그룹에 대한 정보를 내재하고 있다고 가정합니다.

• Sampling Grid: 입력 이미지 위에 $M \times M$ 크기의 샘플링 그리드가 설정됩니다. 이 격자의 각 점(anchor point)은 이후 단계에서 어텐션 맵을 병합하기 위한 시작점 역할을 합니다.

• Attention Aggregation: Stable Diffusion 모델의 다양한 해상도(예: 8x8, 16x16, 32x32, 64x64)에서 추출된 어텐션 텐서를 집계(aggregate)합니다. 각 해상도의 어텐션 맵은 이미지의 다른 스케일의 정보(낮은 해상도는 넓은 영역, 높은 해상도는 세부 정보)를 담고 있습니다. 이 단계에서는 모든 어텐션 맵의 공간 해상도를 최고 해상도(예: 64x64)로 통일한 후, 각 해상도별 중요도(해상도에 비례)에 따라 가중 평균하여 최종 집계 어텐션 텐서 $A_f$를 생성합니다.

• Iterative Attention Merging: 집계된 어텐션 텐서 $A_f$에서 샘플링 그리드의 각 앵커 포인트에 해당하는 어텐션 맵을 초기 제안(proposal)으로 사용합니다. 그 후, 이 제안 목록에 있는 어텐션 맵들 간의 유사도(similarity)를 측정하여 유사도가 높은 맵들을 반복적으로 병합합니다 ($N$번 반복). 어텐션 맵 간의 유사도는 KL 발산(KL divergence)을 사용하여 측정됩니다.

• Non-Maximum Suppression: 반복적인 병합 과정을 거쳐 최종 객체 제안 목록 $L_p$가 생성됩니다. 각 제안은 확률 맵 형태로 되어 있으며, 특정 객체/영역에 속할 픽셀들의 활성화 정도를 나타냅니다. 마지막으로, 모든 제안을 원본 이미지 해상도(512x512)로 업샘플링한 후, 각 픽셀 위치에서 가장 높은 활성화 값을 가지는 제안의 인덱스를 선택하여 최종 분할 마스크 $S$를 생성합니다.

DiffSeg는 이러한 과정을 통해 어떠한 추가 학습이나 언어적 정보(텍스트 프롬프트 등) 없이도 이미지를 분할할 수 있습니다.

2. Related Works

• 확산 모델(Diffusion Models)
  이 섹션은 DiffSeg가 기반으로 하는 사전 학습된 안정적 확산 모델(stable diffusion models)에 대해 언급합니다. 기존 연구들이 이러한 모델의 판별적인 시각적 특징을 활용하여 제로샷 분류, 지도 방식 분할 등 다양한 컴퓨터 비전 작업을 수행했음을 설명합니다. DiffSeg는 이러한 모델의 자기 주의(self-attention) 레이어에서 객체 그룹화 정보가 나타난다는 점을 이용하여 추가 학습 없이 분할을 수행한다는 차이점을 강조합니다.

• 비지도 분할(Unsupervised Segmentation)
  어떠한 주석(annotations) 없이 이미지에 대한 조밀한 분할 마스크를 생성하는 것을 목표로 하는 비지도 분할 분야를 다룹니다. 많은 기존 연구들은 좋은 성능을 위해 타겟 데이터셋에 대한 비지도 학습이 필요하며, 이는 제로샷이 아니라는 한계를 가집니다.

• 제로샷 전이 분할(Zero-Shot Transfer Segmentation)
  학습 시 보지 못한 카테고리의 이미지까지 분할할 수 있는 능력을 의미합니다. SAM 📄 Segment Anything과 같은 최근 연구들은 대규모 주석으로 학습하여 뛰어난 제로샷 성능을 보이지만, 주석 수집 비용이 매우 높습니다. 일부 제로샷 연구들은 추가적인 이미지 ReCo나 텍스트 입력 MaskCLIP을 필요로 합니다. 하지만 DiffSeg는 사전 학습된 안정적 확산 모델의 자기 주의 레이어를 활용하여 어떠한 주석이나 추가적인 외부 정보 없이도 이미지 분할을 수행하는 비지도 및 제로샷 분할 방법이라는 점에서 기존 연구들과 차별화됩니다.

3. Method

3.1 Stable Diffusion Model Review

• 확산 모델 계열: Stable Diffusion 모델은 이미지 생성 모델인 확산 모델(Diffusion Model)의 인기 있는 변형입니다.

• 두 가지 과정: 확산 모델은 크게 두 가지 과정으로 이루어집니다.

  • Forward Pass (정방향 과정): 각 시간 단계마다 소량의 가우시안 노이즈(Gaussian noise)가 반복적으로 이미지에 추가되어 이미지가 최종적으로 순수한 가우시안 노이즈로 변환됩니다.
  • Reverse Pass (역방향 과정): 이 과정에서 확산 모델은 노이즈 이미지를 원래의 깨끗한 이미지로 복원하도록 학습됩니다. 즉, 노이즈를 반복적으로 제거하는 방법을 배웁니다.

• 모델 구조: Stable Diffusion 모델은 인코더(encoder)-디코더(decoder) 구조와 U-Net 디자인을 사용하며, 이 구조 안에 어텐션 레이어(attention layers)가 포함되어 있습니다.

• 잠재 공간 활용:

  • 먼저 인코더($E$)를 사용하여 크기가 $H \times W \times 3$인 입력 이미지 $\mathbf{x} \in \mathbb{R}^{H \times W \times 3}$를 공간 차원이 더 작은 잠재 공간(latent space) 표현 $\mathbf{z} \in \mathbb{R}^{h \times w \times c}$으로 압축합니다.
  • 이 과정은 다음과 같은 공식으로 표현됩니다:
    $\mathbf{z} = E(\mathbf{x})$
    • $\mathbf{x}$: 원본 입력 이미지 (높이 $H$, 너비 $W$, 채널 수 3).
    • $E$: 이미지를 잠재 공간으로 압축하는 인코더 함수.
    • $\mathbf{z}$: 잠재 공간에 표현된 이미지 (높이 $h$, 너비 $w$, 채널 수 $c$, 여기서 $h < H$, $w < W$).
  • 압축된 잠재 표현 $\mathbf{z}$는 디코더($D$)를 통해 원본 이미지와 유사한 $\tilde{\mathbf{x}} = D(\mathbf{z})$로 다시 변환될 수 있습니다.
  • 이 논문에서 주목하는 확산 과정은 모두 잠재 공간에서 U-Net 아키텍처를 통해 일어납니다. 잠재 공간에서 작업을 수행함으로써 픽셀 공간보다 훨씬 효율적으로 연산을 처리할 수 있습니다.

• U-Net의 중요성: 본 논문은 특히 Stable Diffusion 모델 내 U-Net 아키텍처의 어텐션 레이어에 집중하여 이미지 세그멘테이션에 활용합니다.

• U-Net 아키텍처 구성: Stable Diffusion 모델의 U-Net 아키텍처는 여러 개의 모듈형 블록으로 구성됩니다. 이 블록 중 16개는 ResNet 레이어와 Transformer 레이어로 이루어져 있습니다.

• Transformer 레이어의 역할: Transformer 레이어는 두 가지 주요 어텐션 메커니즘을 사용합니다.

  • Self-Attention: 이미지 전체의 전역적 어텐션을 학습합니다. 즉, 이미지 내의 한 부분이 이미지의 다른 모든 부분과 얼마나 관련되어 있는지를 학습합니다.
  • Cross-Attention: 이미지와 선택적 텍스트 입력 간의 어텐션을 학습합니다. 이는 텍스트 프롬프트와 이미지 내용 간의 관련성을 파악하는 데 사용됩니다.

• Self-Attention 레이어의 중요성: 이 논문에서는 Self-Attention 레이어에 주목합니다. U-Net 아키텍처의 16개 복합 블록에 총 16개의 Self-Attention 레이어가 있으며, 각각 4차원의 어텐션 텐서 $A_k \in \mathbb{R}^{h_k \times w_k \times h_k \times w_k}$를 생성합니다. ($k=1, \dots, 16$)

  • $A_k \in \mathbb{R}^{h_k \times w_k \times h_k \times w_k}$ 텐서의 각 차원은 다음과 같은 의미를 가집니다.
    • 첫 번째 두 차원 ($h_k \times w_k$): Query의 공간 위치 (I, J)를 나타냅니다. 이미지 그리드의 어느 위치에서 Query가 시작되는지를 의미합니다.
    • 나머지 두 차원 ($h_k \times w_k$): Key (또는 Value)의 공간 위치 (y, z)를 나타냅니다. Query 위치 (I, J)가 이미지 그리드의 다른 모든 위치 (y, z)에 얼마나 '어텐션'을 기울이는지, 즉 Query (I, J)와 Key (y, z) 간의 유사도 또는 관련성 정도를 나타냅니다.
  • 따라서 텐서 $A_k$는 모든 Query 위치 (I, J) (총 $h_k \times w_k$개) 각각에 대해, 해당 Query가 이미지의 모든 Key 위치 (y, z) (총 $h_k \times w_k$개)에 주는 어텐션 가중치 맵 (크기 $h_k \times w_k$)을 저장하는 구조가 됩니다. 이를 합치면 총 $h_k \times w_k \times h_k \times w_k$의 4차원 텐서가 되는 것입니다.
  • 논문에서 언급된 것처럼, 실제 구현에서는 멀티-헤드 어텐션으로 인해 헤드(head) 차원이 추가되어 5차원이 되지만, 이 논문에서는 헤드 차원을 따라 평균하여 4차원으로 단순화하여 분석했습니다.

  수식으로 표현하면:

  $A_k \in \mathbb{R}^{h_k \times w_k \times h_k \times w_k}$

  여기서 $A_k[I, J, y, z]$는 Query 위치 (I, J)와 Key 위치 (y, z) 간의 어텐션 가중치를 의미합니다.

• 핵심 가설: 저자들은 이전 연구(DiffuMask)에서 Cross-Attention 레이어가 텍스트 프롬프트로 참조될 때 객체 그룹핑 정보를 포함한다는 것을 보인 것에 영감을 받아, unconditional Self-Attention 또한 이미지 속 객체 그룹핑에 대한 내재적 정보를 포함하며 이를 텍스트 입력 없이도 세그멘테이션 마스크 생성에 사용할 수 있다고 가정합니다.

• 어텐션 텐서의 의미: 각 어텐션 텐서 $A_k$에서 특정 공간 위치 (I, J)에 해당하는 2D 어텐션 맵 $A_k[I, J, :, :] \in \mathbb{R}^{h_k \times w_k}$는 해당 위치 (I, J)와 이미지의 모든 다른 위치 간의 의미론적 상관관계를 포착합니다. 위치 (I, J)는 원래 이미지 픽셀 공간의 특정 영역에 해당하며, 이 영역의 크기는 텐서의 receptive field에 따라 달라집니다.

• 두 가지 중요한 관찰: 저자들은 Self-Attention 텐서를 시각화하며 다음과 같은 두 가지 특성을 관찰했습니다 (그림 2 참고).

  • Intra-Attention Similarity (어텐션 내 유사성): 2D 어텐션 맵 $A_k[I, J, :, :]$ 내에서, 위치 (I, J)와 동일한 객체 그룹에 해당하는 위치들은 강한 응답(높은 어텐션 값)을 보이는 경향이 있습니다. 예를 들어, (I, J)와 (I+1, J+1)이 같은 객체에 속한다면 $A_k[I, J, I+1, J+1]$ 값이 클 가능성이 높습니다.
  • Inter-Attention Similarity (어텐션 간 유사성): 두 개의 2D 어텐션 맵 $A_k[I, J, :, :]$와 $A_k[I+1, J+1, :, :]$ 사이에서, 만약 위치 (I, J)와 (I+1, J+1)이 원래 이미지 공간에서 동일한 객체 그룹에 속한다면, 이 두 어텐션 맵은 유사한 패턴을 공유하는 경향이 있습니다.

• 어텐션 맵의 해상도: 어텐션 맵은 다양한 해상도(예: 8x8, 16x16, 32x32, 64x64)로 존재합니다. 여기서 해상도는 어텐션 맵 자체의 공간 크기를 의미합니다.

• 해상도와 수용 영역의 관계:

  • 어텐션 맵의 해상도가 낮을수록 (예: 8x8 맵의 한 위치가 64x64 맵의 여러 위치에 해당) 원본 이미지에서 더 넓은 영역을 커버하는 '수용 영역'을 가집니다. 이는 낮은 해상도 맵이 큰 객체나 객체 그룹 전체를 파악하는 데 유리함을 의미합니다.
  • 반대로 어텐션 맵의 해상도가 높을수록 (예: 64x64) 원본 이미지에서 더 작은 영역을 커버하는 '수용 영역'을 가집니다. 이는 높은 해상도 맵이 객체의 세부적인 구성 요소나 작은 객체를 파악하는 데 유리함을 의미합니다.

• 객체 그룹화: 논문의 저자들은 이러한 어텐션 맵, 특히 self-attention 맵에 시각적으로 유사한 특징을 공유하는 객체나 객체 부위들이 함께 그룹화되는 정보가 내재되어 있음을 발견했습니다. 낮은 해상도 맵은 전반적인 객체 그룹을, 높은 해상도 맵은 객체의 세부적인 부분을 포착하는 경향이 있습니다.

• 여러 해상도 사용의 중요성: Stable Diffusion 모델이 다양한 해상도의 어텐션 맵을 생성하기 때문에, 이 논문에서는 모든 해상도의 어텐션 맵을 결합(aggregation)하는 방식을 제안합니다. 이는 큰 객체의 일관된 그룹화 정보와 작은 객체나 객체 세부사항에 대한 미세한 정보를 모두 활용하여 더 나은 세그멘테이션 결과를 얻기 위함입니다.

이러한 어텐션 맵의 특성은 Stable Diffusion 모델이 단순히 이미지를 생성하는 것뿐만 아니라 이미지 내의 객체 구조와 의미론적 관계를 이해하고 있음을 시사하며, 이를 통해 레이블링되지 않은 이미지에서도 객체를 분할하는 DiffSeg와 같은 비지도(unsupervised) 및 제로샷(zero-shot) 세그멘테이션 작업이 가능해집니다.

그림2

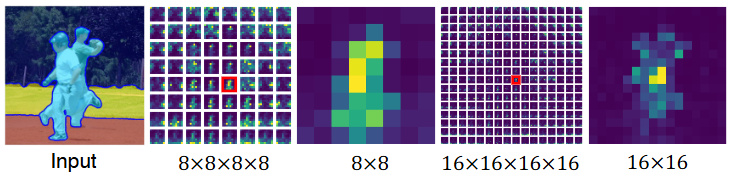
• Input: 원본 이미지와 그 위에 겹쳐진 파란색 윤곽선의 하늘색 마스크를 보여줍니다. 이 마스크는 DiffSeg 방법으로 얻은 세그멘테이션 결과이며, 이미지 속 두 사람을 하나의 객체 그룹으로 묶어 보여줍니다. DiffSeg는 이처럼 사전에 정의된 카테고리 없이 이미지 내 객체를 자동으로 분할하는 비지도(unsupervised) 세그멘테이션을 수행합니다.

• 8x8x8x8: Stable Diffusion 모델 내 8x8 해상도의 self-attention layer에서 추출된 attention 텐서($A^k \in \mathbb{R}^{8 \times 8 \times 8 \times 8}$)의 일부를 보여줍니다. 이 텐서는 8x8 그리드의 각 위치에 해당하는 2D attention map($A^k[I, J, :, :]$)들로 구성됩니다. 빨간색 상자는 특정 위치 (I, J)에 해당하는 attention map을 강조한 것입니다.

• 8x8: 위 8x8x8x8 그리드의 빨간색 상자로 강조된 2D attention map을 확대하여 보여줍니다. 이 맵은 8x8 해상도에서 선택된 위치와 다른 모든 위치 간의 semantic correlation 정도를 나타냅니다. 밝은 노란색 영역은 높은 attention 값을 의미하며, 선택된 위치와 해당 영역이 강하게 연관되어 있음을 보여줍니다. 이 맵은 이미지 내에서 두 사람을 모두 포함하는 넓은 영역에 높은 attention을 보이며, 낮은 해상도의 attention 맵은 더 넓은 receptive field를 가져 큰 객체 그룹을 포착하는 데 유리함을 알 수 있습니다.

• 16x16x16x16: Stable Diffusion 모델 내 16x16 해상도의 self-attention layer에서 추출된 attention 텐서($A^k \in \mathbb{R}^{16 \times 16 \times 16 \times 16}$)의 일부를 보여줍니다. 마찬가지로 16x16 그리드의 각 위치에 해당하는 2D attention map들로 구성됩니다. 빨간색 상자는 특정 위치에 해당하는 attention map을 강조한 것입니다.

• 16x16: 위 16x16x16x16 그리드의 빨간색 상자로 강조된 2D attention map을 확대하여 보여줍니다. 이 맵은 16x16 해상도에서 선택된 위치와 다른 모든 위치 간의 semantic correlation을 나타냅니다. 8x8 맵과 비교했을 때, 이 맵은 객체 그룹 내의 더 작고 세분화된 부분(예: 한 사람의 상체 일부)에 높은 attention을 보입니다. 이는 높은 해상도의 attention 맵이 더 작은 receptive field를 가져 객체의 미세한 부분이나 작은 객체를 식별하는 데 유리함을 보여줍니다.

A Note on Extracting Attention Maps.

• 이 연구에서의 방법:

  • 무조건적 잠재 공간(unconditioned latent) 사용: 텍스트 프롬프트를 사용하지 않고, 무조건적인 텍스트 임베딩을 사용하여 계산된 무조건적 잠재 공간만 사용합니다. 이는 특정 조건(프롬프트)에 의존하지 않고 이미지 자체의 특징을 추출하기 위함입니다.

  • 확산 과정 1회 실행: 일반적으로 여러 단계를 거치는 확산 과정을 단 한 번만 실행합니다.

  • 큰 시간 단계(time-step variable t) 설정: 시간 단계 변수 t를 큰 값(예: 300)으로 설정합니다. Stable Diffusion 모델의 관점에서 볼 때, 확산 과정은 노이즈를 제거하여 깨끗한 이미지를 복구하는 역 과정으로 학습됩니다. 시간 단계 t는 현재 노이즈 레벨을 나타내며, t가 크면 노이즈가 많은 상태, t가 작으면 노이즈가 적은(깨끗한) 상태를 의미합니다. 따라서 t를 크게 설정하고 확산 과정을 1회만 실행하면, 모델은 입력된 실제 이미지를 이미 노이즈가 거의 제거된 상태의 생성된 이미지로 인식하게 됩니다. 이렇게 함으로써 이미지 생성 과정의 중간 단계에서 어텐션 맵을 효율적으로 얻을 수 있습니다.

3.2. DiffSeg

attention 텐서를 유효한 segmentation mask로 집계하고 병합하는 과정

Attention Aggregation

이 단계에서는 다양한 해상도를 가진 어텐션 텐서들을 하나의 고해상도 텐서로 결합합니다.

• 입력 텐서: Stable Diffusion 모델의 U-Net을 통과한 입력 이미지로부터 총 16개의 자기 어텐션 텐서($A_k$)를 얻습니다. 이 텐서들은 다양한 공간 해상도(8x8, 16x16, 32x32, 64x64)를 가집니다. 구체적으로는 64x64 해상도의 텐서 5개, 32x32 해상도의 텐서 5개, 16x16 해상도의 텐서 5개, 그리고 8x8 해상도의 텐서 1개로 구성됩니다. (참고: 논문 본문에 64x64 5개, 32x32 5개, 16x16 5개, 8x8 1개로 언급되어 있으나, 수식 (1) 옆의 설명에 16개 텐서가 있다고 되어 있어, 총 16개 텐서가 맞습니다.) 각 텐서 $A_k$는 4차원이며, 형태는 $R^{h_k \times w_k \times h_k \times w_k}$ 입니다. 여기서 $(h_k, w_k)$는 해당 텐서의 해상도입니다.
• 텐서 구조의 의미: 4차원 텐서 $A_k[I, J, :, :]$ 에서 앞의 두 차원 $(I, J)$는 원본 이미지 공간의 특정 위치에 해당하며, 뒤의 두 차원 $(:, :)$는 해당 위치 $(I, J)$와 이미지 내 모든 다른 공간 위치들 사이의 의미론적 상관관계를 나타내는 2D 어텐션 맵입니다. 즉, $A_k[I, J, y, z]$ 값은 위치 $(I, J)$와 위치 $(y, z)$가 얼마나 관련이 있는지를 나타냅니다.

후반 2차원 업샘플링

어텐션 맵 자체($:, :$에 해당하는 후반 2차원)는 해상도와 관계없이 공간적으로 일관된 정보를 담고 있습니다. 따라서 모든 텐서의 후반 2차원(어텐션 맵 부분)을 가장 높은 해상도인 64x64로 바이리니어 보간법(Bilinear interpolation)을 사용하여 업샘플링합니다.
수식: $\tilde{A}_k = \text{Bilinear-upsample}(A_k) \in R^{h_k \times w_k \times 64 \times 64}$
이는 각 해상도의 어텐션 맵을 모두 동일한 64x64 크기로 맞추는 과정입니다.

전반 2차원 업샘플링

우리가 목표로 하는 것은 최종적으로 64x64 해상도의 어텐션 텐서 $A_f$를 만드는 것입니다. 이 $A_f$의 각 위치 $[I, J]$에 해당하는 2D 어텐션 맵 $A_f[I, J, :, :]$ (이 맵은 64x64 크기)을 계산하는 것이 목표입니다. 이 맵은 원본 이미지의 $(I, J)$ 위치와 다른 모든 위치들 간의 상관관계를 최종적으로 나타냅니다.

이 최종 맵 $A_f[I, J, :, :]$은 Stable Diffusion 모델에서 나온 다양한 해상도(8x8, 16x16, 32x32, 64x64)의 어텐션 텐서들에서 얻은 어텐션 맵들을 가중 평균하여 만듭니다.

수식은 아래와 같습니다.

• $A_f[I, J, :, :]$: 최종 64x64 텐서에서 특정 위치 $(I, J)$에 해당하는 64x64 어텐션 맵입니다. 여기서 $(I, J)$는 0부터 63까지의 값을 가질 수 있습니다.

• $\tilde{A}_k$: 원본 텐서 $A_k$의 뒤 2차원(어텐션 맵 부분)을 64x64로 업샘플링한 텐서입니다. $\tilde{A}_k$의 크기는 $h_k \times w_k \times 64 \times 64$ 입니다. ($h_k, w_k$는 원본 텐서의 해상도)

• $[I / \sigma_k, J / \sigma_k]$: 이 부분이 핵심입니다. 최종 64x64 위치 $(I, J)$가 원본 해상도 $w_k$의 텐서에서 어떤 위치에 해당하는가를 계산하는 것입니다.

  • $\sigma_k = 64 / w_k$ 는 해상도 차이를 보정하는 스케일링 계수입니다.
  • $/$는 플로어 나눗셈(소수점 이하 버림)입니다.
  • 결과적으로 $[I / \sigma_k, J / \sigma_k]$는 원본 해상도 텐서 $\tilde{A}_k$ 내에서 특정 위치를 나타냅니다.

• $\tilde{A}_k[I / \sigma_k, J / \sigma_k, :, :]$: $\tilde{A}_k$ 텐서에서 계산된 위치 $[I / \sigma_k, J / \sigma_k]$에 해당하는 64x64 어텐션 맵입니다.

• $R_k$: 해상도 $k$의 어텐션 맵에 부여하는 가중치입니다. 논문에서는 $R_k \propto w_k$ (해상도에 비례) 방식을 사용합니다. 모든 $R_k$의 합은 1입니다.

• $\sum_{k \in \{1, ..., 16\}}$: 모든 16개의 다양한 해상도 어텐션 텐서에 대해 위 과정을 반복하여 얻은 맵들을 모두 더합니다.

예시

우리가 최종 64x64 어텐션 텐서 $A_f$의 특정 위치, 예를 들어 $(I, J) = (10, 20)$에 해당하는 어텐션 맵 $A_f[10, 20, :, :]$을 계산한다고 가정해 봅시다. Stable Diffusion 모델에서 나온 텐서들 중 다음 해상도의 텐서들이 있다고 상상해 봅시다.

1. 64x64 해상도 텐서 (예: $A_1$)

   • $w_1 = 64$. 스케일링 계수 $\sigma_1 = 64 / 64 = 1$.
   • 원본 텐서 $A_1$ (뒤 2차원 64x64로 업샘플링되어 $\tilde{A}_1$ 상태)에서 가져올 위치: $[10 / 1, 20 / 1] = [10, 20]$
   • 가져오는 맵: $\tilde{A}_1[10, 20, :, :]$
   • 이 맵에 곱할 가중치: $R_1$ (64x64 해상도에 해당하는 가중치)

2. 32x32 해상도 텐서 (예: $A_2$)

   • $w_2 = 32$. 스케일링 계수 $\sigma_2 = 64 / 32 = 2$.
   • 원본 텐서 $A_2$ (뒤 2차원 64x64로 업샘플링되어 $\tilde{A}_2$ 상태)에서 가져올 위치: $[10 / 2, 20 / 2] = [5, 10]$
   • 가져오는 맵: $\tilde{A}_2[5, 10, :, :]$
   • 이 맵에 곱할 가중치: $R_2$ (32x32 해상도에 해당하는 가중치)

3. 16x16 해상도 텐서 (예: $A_3$)

   • $w_3 = 16$. 스케일링 계수 $\sigma_3 = 64 / 16 = 4$.
   • 원본 텐서 $A_3$ (뒤 2차원 64x64로 업샘플링되어 $\tilde{A}_3$ 상태)에서 가져올 위치: $[10 / 4, 20 / 4] = [2, 5]$ (플로어 나눗셈)
   • 가져오는 맵: $\tilde{A}_3[2, 5, :, :]$
   • 이 맵에 곱할 가중치: $R_3$ (16x16 해상도에 해당하는 가중치)

4. 8x8 해상도 텐서 (예: $A_4$)

   • $w_4 = 8$. 스케일링 계수 $\sigma_4 = 64 / 8 = 8$.
   • 원본 텐서 $A_4$ (뒤 2차원 64x64로 업샘플링되어 $\tilde{A}_4$ 상태)에서 가져올 위치: $[10 / 8, 20 / 8] = [1, 2]$ (플로어 나눗셈)
   • 가져오는 맵: $\tilde{A}_4[1, 2, :, :]$
   • 이 맵에 곱할 가중치: $R_4$ (8x8 해상도에 해당하는 가중치)

(실제로는 각 해상도별로 여러 개의 텐서가 있으므로, 해당 해상도의 모든 텐서에 대해 동일한 위치에서 맵을 가져온 후 가중치 $R_k$를 적용하고 모두 더해야 합니다. 논문의 $\sum$은 이 모든 텐서들을 포함합니다.)

최종 64x64 어텐션 텐서의 위치 $(10, 20)$에 해당하는 맵 $A_f[10, 20, :, :]$은 위에서 가져온 각 해상도의 맵들을 해당 가중치 $R_k$로 곱한 후 모두 더하여 만들어집니다.

$A_f[10, 20, :, :] = (\tilde{A}_1[10, 20, :, :] \times R_1) + (\tilde{A}_2[5, 10, :, :] \times R_2) + (\tilde{A}_3[2, 5, :, :] \times R_3) + (\tilde{A}_4[1, 2, :, :] \times R_4) + \dots$ (모든 16개 텐서에 대해 반복)

이것이 의미하는 바는 무엇일까요?

• 64x64 텐서의 위치 $(10, 20)$은 원본 이미지의 비교적 작은 영역에 해당합니다.
• 32x32 텐서의 위치 $(5, 10)$은 원본 이미지에서 64x64 텐서의 $(10, 20)$ 위치를 포함하는 더 넓은 영역에 해당합니다 (Receptive Field가 더 넓기 때문).
• 16x16 텐서의 위치 $(2, 5)$는 32x32 텐서의 $(5, 10)$ 위치를 포함하는 더 넓은 영역에 해당하고, 8x8 텐서의 위치 $(1, 2)$는 16x16 텐서의 $(2, 5)$ 위치를 포함하는 훨씬 더 넓은 영역에 해당합니다.

따라서 최종 어텐션 맵 $A_f[10, 20, :, :]$는 다양한 스케일(해상도)에서 얻은 정보를 결합하여 만들어집니다.

• 64x64 맵 ($[10, 20]$에서 가져온 것): 원본 이미지의 작은 영역에 대한 세밀한 어텐션 정보를 제공합니다.
• 32x32 맵 ($[5, 10]$에서 가져온 것): 원본 이미지의 조금 더 넓은 영역에 대한 어텐션 정보를 제공합니다.
• 16x16 맵 ($[2, 5]$에서 가져온 것): 원본 이미지의 더 넓은 영역에 대한 어텐션 정보를 제공합니다.
• 8x8 맵 ($[1, 2]$에서 가져온 것): 원본 이미지의 가장 넓은 영역에 대한 어텐션 정보를 제공합니다.

논문에서 사용하는 비례 가중치($R_k \propto w_k$)는 고해상도 맵(예: 64x64)에 더 큰 가중치를 부여하여 세부적인 정보를 더 중요하게 여기고, 저해상도 맵(예: 8x8)에는 작은 가중치를 부여하여 전반적인 맥락 정보를 보조적으로 활용하겠다는 의미입니다. 그림 4에서 보듯이, 고해상도 맵만 사용하면 세그멘테이션이 조각나고(fractured), 저해상도 맵만 사용하면 객체 경계가 뭉개지는(coarse) 문제가 발생하는데, 이 가중 평균을 통해 다양한 스케일의 정보를 조화롭게 결합하여 균형 잡힌 세그멘테이션을 얻으려는 것입니다.

그림3

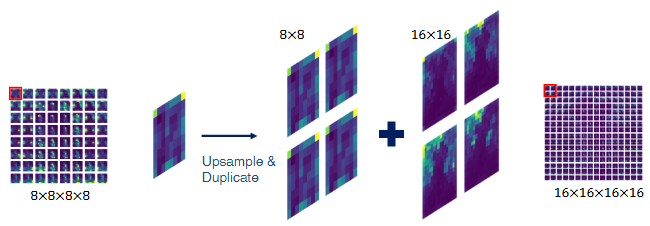
해당 이미지는 DiffSeg 방법의 주요 단계 중 하나인 Attention Aggregation 과정을 그림으로 설명하고 있습니다. 이 과정의 목적은 Stable Diffusion 모델의 여러 해상도 Self-Attention 레이어에서 얻은 어텐션 정보를 하나의 일관된 텐서로 결합하는 것입니다.

이 그림은 8x8 해상도의 어텐션 맵을 16x16 해상도로 집계하는 단순화된 예시를 보여줍니다. 논문에서는 8x8, 16x16, 32x32, 64x64 해상도의 모든 어텐션 텐서를 64x64 해상도로 집계합니다.

그림의 각 단계를 상세히 설명하면 다음과 같습니다.

• 8x8x8x8 (왼쪽): Stable Diffusion 모델의 낮은 해상도(예: 8x8) Self-Attention 레이어에서 얻은 어텐션 텐서의 일부를 보여줍니다. 이 텐서는 4차원이며, 처음 두 차원은 참조 위치 $(I, J)$를, 마지막 두 차원은 해당 위치 $(I, J)$와 이미지의 모든 위치 간의 공간적 상관관계를 나타내는 2D 어텐션 맵 $\in \mathbb{R}^{8 \times 8}$을 포함합니다. 그림의 빨간색 사각형은 특정 참조 위치에 대한 하나의 8x8 어텐션 맵을 강조합니다.
• Upsample & Duplicate (중앙 왼쪽): 8x8 어텐션 맵 하나를 가져와서 Upsample 및 Duplicate 과정을 거칩니다.
  • Upsample: 어텐션 맵 자체의 공간 해상도를 더 높은 해상도(예: 16x16, 논문 실제 구현에서는 64x64)로 높입니다. Bilinear interpolation 등의 방법을 사용합니다. 논문 수식 (2)는 이 과정을 나타내며, 각 어텐션 텐서 $A^k \in \mathbb{R}^{h_k \times w_k \times h_k \times w_k}$의 마지막 두 차원 $(h_k \times w_k)$를 64x64로 업샘플링하여 $\tilde{A}^k \in \mathbb{R}^{h_k \times w_k \times 64 \times 64}$를 만듭니다:
    $$ \tilde{A}^k = \text{Bilinear-upsample}(A^k) \in \mathbb{R}^{h_k \times w_k \times 64 \times 64} $$
  • Duplicate: 낮은 해상도의 어텐션 맵은 더 넓은 영역(수용장, receptive field)을 커버합니다. 그림은 8x8 맵 하나가 16x16 맵의 2x2 블록 영역에 해당함을 보여줍니다. 따라서 낮은 해상도 맵을 업샘플링한 후, 해당 낮은 해상도 위치가 커버하는 높은 해상도의 여러 위치에 대해 동일한 업샘플링된 맵을 복제하여 정렬합니다.
• 8x8 및 16x16 맵 (중앙 오른쪽): Duplicate 과정을 거친 업샘플링된 8x8 맵(이제 16x16 해상도) 4개와, 집계하려는 목표 해상도(16x16)의 텐서에서 동일한 2x2 블록 위치에 해당하는 16x16 어텐션 맵 4개를 보여줍니다. '+' 기호는 이 두 종류의 맵들을 결합(더하는)함을 의미합니다.
• 16x16x16x16 (오른쪽): 결합 결과로 생성된 최종 집계 어텐션 텐서(그림 예시에서는 16x16 해상도)의 일부를 보여줍니다. 빨간색 사각형은 집계 결과 텐서의 특정 참조 위치에 해당하는 어텐션 맵을 강조합니다. 논문 실제 구현에서는 모든 해상도의 텐서가 64x64 텐서로 집계됩니다. 논문 수식 (3)은 이 최종 집계 과정을 설명합니다:
  $A_f[I, J, :, :] = \sum_{k \in \{1,...,16\}} \tilde{A}_k[I/\sigma_k, J/\sigma_k, :, :] \ast R_k$
  여기서 $\sigma_k = 64/w_k$는 해상도 비율이며, $I/\sigma_k$와 $J/\sigma_k$는 바닥 나눗셈(floor division)으로 해당 높은 해상도 위치 $(I, J)$에 대응하는 낮은 해상도 텐서의 위치를 찾습니다. $R_k$는 각 해상도 어텐션 맵의 중요도 가중치입니다. 논문에서는 해상도에 비례하는 가중치 방식을 사용합니다. 집계 후에는 최종 맵 $A_f[I, J, :, :]$을 확률 분포가 되도록 정규화합니다.

이처럼 Attention Aggregation은 다양한 해상도의 어텐션 정보를 공간적으로 일관되게 결합하여, 객체에 대한 전반적인 정보와 미세한 정보를 모두 포함하는 풍부한 어텐션 텐서를 생성합니다. 이렇게 생성된 텐서는 이후 Iterative Attention Merging 단계에서 세분화 마스크 생성에 사용됩니다.

Iterative Attention Merging

이 섹션은 DiffSeg 알고리즘의 두 번째 구성요소인 이 단계의 목표는 Stable Diffusion 모델의 자기 주의(self-attention) 레이어에서 추출된 어텐션 맵들을 병합하여 최종적인 객체 또는 영역 제안(object proposals)을 생성하는 것입니다.

• 목표: 이전 단계에서 생성된 64x64 해상도의 어텐션 텐서 $A_f$에 포함된 어텐션 맵들을 병합하여 이미지 내 객체 또는 영역을 나타내는 제안 목록($L_p$)을 만듭니다. 각 제안은 하나의 객체 또는 영역 카테고리의 활성화를 포함할 가능성이 높습니다.

• 기존 방법과의 비교 (K-Means):

  • 기존의 비지도 세그멘테이션 방법들([11], [16], [24])에서는 K-Means 클러스터링 알고리즘을 사용하여 어텐션 텐서 $A_f$로부터 객체 클러스터를 찾는 방식이 사용되었습니다.
  • 하지만 K-Means는 클러스터의 개수를 미리 지정해야 하는 단점이 있습니다. 논문의 저자들은 "야생(in the wild)" 이미지처럼 카테고리를 알 수 없는 이미지에 대해 세그멘테이션을 수행하는 경우 클러스터 개수를 정하는 것이 직관적이지 않은 하이퍼파라미터라고 지적합니다.
  • 또한 K-Means는 초기화에 따라 결과가 달라지는 확률론적인(stochastic) 특성을 가지므로, 동일한 이미지에 대해서도 실행할 때마다 결과가 크게 달라질 수 있습니다.

• DiffSeg의 접근 방식: DiffSeg는 K-Means의 이러한 단점을 피하기 위해 샘플링 격자(sampling grid)에서 시작하여 어텐션 맵을 반복적으로 병합하는 방식을 제안합니다.

  • 샘플링 격자 생성: 먼저 M x M 크기의 균일한 간격의 앵커 포인트($\mathcal{M} = \{(i_m, j_m) | m = 1, ..., M^2\}$)를 생성합니다 (1 <= M <= 64). 논문에서는 M=16을 사용하여 총 256개의 앵커 포인트를 생성합니다.
  • 앵커 어텐션 맵 추출: 이 앵커 포인트에 해당하는 어텐션 맵들을 어텐션 텐서 $A_f$에서 추출하여 앵커 목록 $L_a$를 만듭니다. 각 앵커 어텐션 맵 $A_f[i_m, j_m, :, :]$는 64x64 해상도를 가집니다.
  • 반복적 어텐션 병합:
    • 어텐션 맵을 병합할 때는 Sec. 3.1에서 언급된 두 가지 관찰(Intra-Attention Similarity와 Inter-Attention Similarity)에 기반합니다.
    • Intra-Attention Similarity: 어텐션 맵 내에서 같은 객체 그룹에 해당하는 위치들이 강한 응답을 보이는 경향이 있습니다.
    • Inter-Attention Similarity: 다른 어텐션 맵 간에 앵커 포인트가 동일한 객체 그룹에 속하는 경우, 어텐션 활성화 패턴이 유사한 경향이 있습니다.

• 유사성 측정 (KL Divergence): 두 어텐션 맵 $A_f[i, j]$와 $A_f[y, z]$ 사이의 유사성은 KL Divergence를 사용하여 측정합니다. 각 어텐션 맵은 유효한 확률 분포이기 때문입니다. "거리" 척도 $D(\cdot)$는 다음과 같이 정의됩니다.

  $2 \cdot D(A_f[i, j], A_f[y, z]) = \left(KL(A_f[i, j] \| A_f[y, z]) + KL(A_f[y, z] \| A_f[i, j])\right)$
  • $A_f[i, j]$와 $A_f[y, z]$: 비교하려는 두 어텐션 맵 (각각 64x64 해상도의 확률 분포).
  • $KL(P \| Q)$: Kullback-Leibler divergence로, 확률 분포 Q에 대한 확률 분포 P의 상대 엔트로피(relative entropy)입니다. 두 분포의 차이를 측정하며 비대칭적인 특성을 가집니다.
  • $KL(A_f[i, j] \| A_f[y, z])$: 첫 번째 맵을 기준으로 두 번째 맵과의 KL Divergence를 계산합니다.
  • $KL(A_f[y, z] \| A_f[i, j])$: 두 번째 맵을 기준으로 첫 번째 맵과의 KL Divergence를 계산합니다.
  • $(KL(\cdot) + KL(\cdot)) / 2$: KL Divergence의 비대칭성을 해결하기 위해 순방향(forward) 및 역방향(reverse) KL Divergence를 모두 계산하여 평균을 취합니다.
  • $D(\cdot)$ 값이 작을수록 두 어텐션 맵의 유사성이 높고, 두 맵의 합(union)이 두 앵커가 속한 동일한 객체를 더 잘 나타낼 가능성이 높다는 것을 의미합니다.

• 병합 프로세스:

  • 총 N번의 반복 병합 과정을 수행합니다.
  • 첫 번째 반복: 앵커 목록 $L_a$의 각 요소와 모든 어텐션 맵 사이의 거리를 $D(\cdot)$를 사용하여 계산합니다. 임계값 하이퍼파라미터 $\tau$를 도입하여, 임계값보다 거리가 작은 모든 어텐션 맵들을 평균화합니다. 이렇게 평균화된 맵들은 새로운 제안 목록 $L_p$에 저장됩니다. 첫 번째 반복에서는 제안 개수가 앵커 개수와 동일합니다.
  • 두 번째 반복부터: 제안 목록 $L_p$ 내의 각 요소와 동일 목록 내의 다른 모든 요소 사이의 거리를 계산합니다. 거리가 임계값 $\tau$보다 작은 요소들을 중복 없이 병합합니다 (평균화). 이 과정을 통해 제안의 개수가 줄어들고, 같은 객체에 속하는 어텐션 맵들이 점진적으로 하나의 제안으로 통합됩니다.

• 결과: 이 반복 병합 단계는 객체 제안 목록 $L_p$를 출력합니다. 각 제안은 64x64 크기의 어텐션 맵 형태입니다.

DiffSeg가 다른 비지도 세그멘테이션 방법들과 차별화되는 지점은 Stable Diffusion 모델의 사전 학습된 어텐션 레이어 정보를 활용하고, K-Means와 같은 기존 클러스터링 방식의 단점(클러스터 수 지정, 확률적 결과)을 개선하여 별도의 학습이나 외부 정보 없이도 임의의 이미지에 대해 안정적인 세그멘테이션 마스크를 생성할 수 있다는 점입니다.

예시 설정:

이미지에 사람 1명과 자동차 1대, 그리고 하늘 배경이 있다고 상상해 봅시다.

1. Attention Aggregation 결과 ($A_f$): 이전 단계를 거쳐 64x64 격자 위치 각각에 대한 64x64 크기의 어텐션 맵이 모인 텐서 $A_f$를 얻었습니다. 이 어텐션 맵들은 각 격자 위치가 이미지의 다른 모든 위치와 얼마나 관련되어 있는지를 나타냅니다. 사람이나 자동차 같은 객체 내부에 있는 격자 위치의 어텐션 맵은 해당 객체의 다른 부분과 강한 상관관계를 보일 것입니다.

2. 샘플링 격자 및 앵커 포인트 생성: DiffSeg는 K-Means처럼 클러스터 개수를 미리 정하는 대신, 이미지의 잠재 공간에 M x M (논문 기본값 16x16) 크기의 앵커 포인트(anchor points) 격자를 생성합니다. 예시에서는 간단하게 2x2 격자를 사용하여 4개의 앵커 포인트를 만들었다고 가정하겠습니다 (M=2, M²=4). 이 4개의 앵커 포인트가 이미지의 잠재 공간에서 다음과 같은 위치에 해당한다고 상상합니다.

   • 앵커 1: 사람의 머리 부분
   • 앵커 2: 사람의 몸 부분
   • 앵커 3: 자동차의 앞부분
   • 앵커 4: 하늘 배경 부분

3. 앵커 어텐션 맵 추출 ($L_a$): 4개의 앵커 포인트 위치에 해당하는 어텐션 맵을 텐서 $A_f$에서 추출합니다. 이것이 초기 앵커 목록 $L_a$가 됩니다.

   • $L_a$ = {Map_Anchor1 (머리), Map_Anchor2 (몸), Map_Anchor3 (자동차), Map_Anchor4 (하늘)}
   • 각 맵은 64x64 크기의 어텐션 맵입니다.

4. 반복적 어텐션 병합 시작 (총 N번 반복): 이제 N번의 병합 과정을 시작합니다. 논문에서는 N=3을 기본값으로 사용합니다.

   • 첫 번째 반복:

     • 목표: 각 앵커 맵과 유사한 모든 어텐션 맵을 $A_f$에서 찾아서 평균화하여 초기 제안을 생성합니다.
     • 과정:
       • Map_Anchor1 (머리)에 대해: $A_f$에 있는 모든 64x64 어텐션 맵과 Map_Anchor1 간의 거리를 KL Divergence 기반 척도 $D(\cdot)$로 계산합니다. 미리 정해둔 임계값 $\tau$보다 거리가 작은 모든 맵 (예: 사람의 머리, 몸, 팔 등 사람 객체와 관련된 다른 위치의 어텐션 맵)을 찾습니다. 이 맵들을 모두 평균합니다. 이 평균화된 맵이 첫 번째 객체 제안 Proposal_A가 됩니다. Proposal_A는 이제 사람 객체 전체를 나타내는 어텐션 패턴을 가질 가능성이 높습니다.
       • Map_Anchor2 (몸)에 대해: 동일하게, Map_Anchor2와 유사한 $A_f$의 모든 맵을 찾아서 평균합니다. Map_Anchor2도 사람에 속하므로, Map_Anchor1과 유사한 맵들과 많이 겹칠 것입니다. 평균 결과는 Proposal_B가 됩니다. Proposal_B도 사람 객체 전체를 나타냅니다.
       • Map_Anchor3 (자동차)에 대해: Map_Anchor3과 유사한 $A_f$의 모든 맵을 찾아서 평균합니다. 결과는 Proposal_C (자동차 객체)가 됩니다.
       • Map_Anchor4 (하늘)에 대해: Map_Anchor4와 유사한 $A_f$의 모든 맵을 찾아서 평균합니다. 결과는 Proposal_D (하늘 배경)가 됩니다.
     • 결과: 첫 번째 반복 후의 제안 목록 $L_p$는 {Proposal_A, Proposal_B, Proposal_C, Proposal_D}가 됩니다. 제안의 개수는 4개로 앵커 개수와 같습니다. (이 단계는 앵커를 seed로 사용하여 초기 제안들을 "생성"하는 단계에 가깝습니다.)

   • 두 번째 반복 (N=2일 경우):

     • 목표: 이제 제안 목록 $L_p$ 내의 제안들끼리 비교하여 유사한 제안을 병합하고 제안 개수를 줄입니다.
     • 과정: $L_p$의 제안들 (Proposal_A, Proposal_B, Proposal_C, Proposal_D) 간의 모든 쌍별 거리를 $D(\cdot)$로 계산합니다.
       • Proposal_A (사람)와 Proposal_B (사람) 비교: 둘 다 사람 객체를 나타내므로, 유사성이 높을 것입니다 ($D(\cdot) < \tau$). 이 두 제안을 병합합니다 (평균). 새로운 제안 Proposal_AB가 생성됩니다. 그리고 병합된 Proposal_A와 Proposal_B는 목록에서 제거됩니다.
       • Proposal_AB (사람)와 Proposal_C (자동차) 비교: 사람과 자동차는 다른 객체이므로 유사성이 낮을 것입니다 ($D(\cdot) \ge \tau$). 병합하지 않습니다.
       • Proposal_AB (사람)와 Proposal_D (하늘) 비교: 사람과 하늘 배경은 다른 영역이므로 유사성이 낮을 것입니다. 병합하지 않습니다.
       • Proposal_C (자동차)와 Proposal_D (하늘) 비교: 자동차와 하늘 배경은 다른 영역이므로 유사성이 낮을 것입니다. 병합하지 않습니다.
     • 결과: 두 번째 반복 후의 제안 목록 $L_p$는 {Proposal_AB, Proposal_C, Proposal_D}가 됩니다. 제안의 개수가 3개로 줄었습니다.

   • 세 번째 반복 (N=3일 경우):

     • 목표: 현재 제안 목록 {Proposal_AB, Proposal_C, Proposal_D} 내의 제안들끼리 다시 비교하고 병합합니다.
     • 과정: 남은 제안들 간의 모든 쌍별 거리를 계산합니다.
       • Proposal_AB (사람), Proposal_C (자동차), Proposal_D (하늘) 간에는 더 이상 유사성이 높은 쌍이 없다고 가정합니다.
     • 결과: 세 번째 반복 후에도 제안 목록 $L_p$는 {Proposal_AB, Proposal_C, Proposal_D} 그대로 유지됩니다. 제안의 개수는 3개입니다.

5. 반복 완료: 총 N번의 반복이 끝나면 최종 제안 목록 $L_p$를 얻습니다. 이 예시에서는 최종적으로 3개의 제안 {Proposal_AB (사람), Proposal_C (자동차), Proposal_D (하늘)}을 얻었습니다. 각 제안은 여전히 64x64 크기의 어텐션 맵 형태입니다.

이후 단계인 Non-Maximum Suppression에서는 이 최종 제안 목록 $L_p$를 사용하여 최종적인 세그멘테이션 마스크를 생성하게 됩니다. 이 과정을 통해 처음의 수많은 어텐션 맵들이 이미지 내의 주요 객체나 영역별로 효과적으로 그룹화되는 것입니다.

Non-Maximum Suppression

Iterative Attention Merging 단계를 통해 여러 개의 객체 제안(object proposals) 목록 $L_p$를 얻었다면, 이제 이 제안들을 최종적인 하나의 세그멘테이션 마스크로 만들어야 합니다. 이 역할을 하는 것이 바로 Non-Maximum Suppression (NMS) 단계입니다. Non-Maximum Suppression의 목적은 여러 제안 중에서 각 픽셀에 대해 가장 적합한 제안을 선택하여 최종적인 세그멘테이션 결과를 확정하는 것입니다. 단계별 설명은 다음과 같습니다.

• 입력: Iterative Attention Merging 단계에서 생성된 객체 제안 목록 $L_p$입니다. 이 목록에는 $N_p$개의 제안이 있으며, 각 제안은 64x64 크기의 어텐션 맵 형태입니다. 각 어텐션 맵은 해당 제안이 이미지의 각 위치에서 얼마나 "활성화"되어 있는지 (즉, 해당 객체에 속할 확률이 높은지)를 나타내는 확률 분포입니다.

• 해상도 일치 (Upsampling):

  • 제안 목록 $L_p$는 64x64 해상도입니다. 하지만 최종 세그멘테이션 마스크는 원본 이미지와 동일한 해상도(논문 기본값 512x512)여야 합니다.
  • 따라서 NMS를 적용하기 전에, $L_p$에 포함된 모든 64x64 어텐션 맵을 bilinear interpolation과 같은 방법을 사용하여 원본 이미지 해상도인 512x512로 업샘플링(upsample) 합니다.
  • 업샘플링된 제안 목록을 $\bar{L}_p$라고 하면, 이는 $N_p \times 512 \times 512$ 크기의 텐서가 됩니다.
    $\bar{L}_p = \text{Bilinear-upsample}(L_p) \in \mathbb{R}^{N_p \times 512 \times 512}$
  • 즉, 이제 각 제안은 원본 이미지 크기의 맵이 되었고, 각 픽셀 위치에 대해 해당 제안이 얼마나 활성화되어 있는지를 나타내는 값을 가집니다.

• 픽셀별 최대값 선택 (argmax):

  • 이제 이미지의 각 픽셀 $(i, j)$ 위치에 대해, 업샘플링된 제안 목록 $\bar{L}_p$의 모든 제안($k = 1, ..., N_p$) 중에서 해당 픽셀에서의 활성화 값이 가장 큰 제안을 찾습니다.
  • 간단히 말해, 512x512 크기의 그리드에서 각 픽셀을 선택하고, 그 픽셀 위치에 해당하는 $\bar{L}_p$의 모든 $N_p$개 제안 값(활성화 값)을 비교합니다.
  • 가장 큰 값을 가진 제안의 인덱스를 해당 픽셀의 최종 세그멘테이션 레이블로 할당합니다.
  • 이것이 바로 Non-Maximum Suppression의 핵심 아이디어입니다: 여러 제안이 특정 영역을 커버할 때, 해당 영역에서 가장 "확신"이 강한 (활성화 값이 가장 높은) 제안 하나만 선택하고 나머지는 "억제(suppress)"하는 것입니다.
  • 최종 세그멘테이션 마스크 $S \in \mathbb{R}^{512 \times 512}$는 다음과 같은 수식으로 표현할 수 있습니다.
    $S[i, j] = \arg \max_{k=1, ..., N_p} \bar{L}_p[k, i, j] \quad \text{for } i, j \in \{0, ..., 511\}$
  • 여기서 $S[i, j]$는 최종 세그멘테이션 마스크의 픽셀 $(i, j)$에 할당된 레이블입니다. 이 레이블은 해당 픽셀에서 활성화 값이 가장 높았던 객체 제안의 인덱스 $k$입니다.
  • Figure 3b의 예시처럼, 여러 색깔로 표시된 제안들이 쌓여 있을 때, 각 픽셀 위치에서 가장 높은 위치에 있는 색깔 (즉, 해당 제안의 활성화 값이 가장 높은)을 최종 픽셀의 색깔로 선택하는 것과 같습니다.

• 결과: NMS 과정을 거치면 각 픽셀이 $1$부터 $N_p$까지의 정수 레이블 중 하나를 가지는 512x512 크기의 최종 세그멘테이션 마스크 $S$를 얻게 됩니다. 이 마스크는 서로 겹치지 않는 영역들로 구성되며, 각 영역은 Iterative Attention Merging 단계에서 생성된 하나의 객체 제안에 해당합니다.

이 단계를 통해 DiffSeg는 사전 학습된 Stable Diffusion 모델의 어텐션 정보를 기반으로, 객체 제안들을 최종적인 픽셀 단위의 세그멘테이션 결과로 변환합니다. 이 마스크는 객체나 영역을 구별하지만, 어떤 객체인지 (예: 사람, 자동차)에 대한 구체적인 의미론적 레이블은 포함하지 않습니다.

1. 예시의 $L_p$와 $N_p$

Iterative Attention Merging 단계의 목표는 수많은 집계된 어텐션 맵($A_f$)을 잠재적인 객체나 영역을 나타내는 소수의 "객체 제안(object proposals)"으로 압축하는 것입니다.

• $L_p$ (객체 제안 목록):

  • Iterative Attention Merging 과정의 최종 결과물입니다.
  • 이것은 단일 세그멘테이션 마스크가 아니라, 이미지 내의 특정 객체나 영역의 "후보(candidate)"들이 담긴 목록 (List) 입니다.
  • 이전 예시에서, 우리는 2x2 앵커 격자에서 시작하여 반복적인 병합 과정을 거쳤습니다. 첫 번째 반복 후 {Proposal_A (머리 기반), Proposal_B (몸 기반), Proposal_C (자동차 기반), Proposal_D (하늘 기반)} 4개의 제안이 생성되었습니다. 두 번째 반복에서 Proposal_A와 Proposal_B가 병합되어 Proposal_AB가 되었습니다. 세 번째 반복에서도 더 이상 병합될 제안이 없다고 가정했습니다.
  • 따라서 이 예시에서의 최종 $L_p$는 {Proposal_AB, Proposal_C, Proposal_D} 입니다.
  • 각 제안(Proposal_AB, Proposal_C, Proposal_D)은 여전히 64x64 크기의 어텐션 맵 형태를 가집니다. 이 맵은 해당 제안이 커버하는 영역(예: 사람, 자동차, 하늘)에서 높은 값을 가집니다.

• $N_p$ (객체 제안의 개수):

  • $L_p$ 목록에 포함된 객체 제안의 총 개수입니다.
  • Iterative Attention Merging 과정을 거치면서 유사한 제안들이 병합되므로, $N_p$는 보통 처음 앵커 개수($M^2$)보다 작아집니다.
  • 이전 예시에서 Iterative Attention Merging 결과 최종 제안 목록 $L_p$는 {Proposal_AB, Proposal_C, Proposal_D} 였습니다.
  • 따라서 이 예시에서의 $N_p$는 3 입니다.

요약하면, 이전 예시에서 Iterative Attention Merging이 끝났을 때, 우리는 3개의 객체 제안(사람 영역, 자동차 영역, 하늘 영역 각각에 대한 확률 맵 형태의 제안)이 담긴 목록 $L_p$를 얻었고, 이 목록의 개수 $N_p$는 3입니다.

2. Non-Maximum Suppression (NMS) 예시

이제 $N_p=3$개의 제안이 담긴 $L_p$ = {Proposal_AB, Proposal_C, Proposal_D} 를 사용하여 최종 세그멘테이션 마스크를 생성하는 NMS 과정을 설명합니다. 원본 이미지 해상도는 512x512라고 가정합니다.

• 단계 1: 제안 해상도 일치 (Upsampling)

  • $L_p$의 각 제안(Proposal_AB, Proposal_C, Proposal_D)은 현재 64x64 크기의 어텐션 맵입니다.
  • 이 3개의 맵을 bilinear interpolation 등을 사용하여 원본 이미지 해상도인 512x512로 키웁니다.
  • 이제 우리는 3개의 512x512 크기의 맵을 가지게 됩니다. 이것이 업샘플링된 제안 목록 $\bar{L}_p$입니다.
  • $\bar{L}_p[1, :, :]$: 512x512 크기의 사람 제안 맵 (Proposal_AB를 업샘플링)
  • $\bar{L}_p[2, :, :]$: 512x512 크기의 자동차 제안 맵 (Proposal_C를 업샘플링)
  • $\bar{L}_p[3, :, :]$: 512x512 크기의 하늘 제안 맵 (Proposal_D를 업샘플링)

• 단계 2: 픽셀별 최대값 선택 (argmax)

  • 이제 512x512 크기의 최종 세그멘테이션 마스크 $S$를 만듭니다. $S$의 각 픽셀 $(i, j)$에 어떤 제안의 레이블을 부여할지 결정합니다.

  • 이미지의 왼쪽 상단 픽셀 $(0, 0)$부터 시작하여 오른쪽 하단 픽셀 $(511, 511)$까지 모든 픽셀에 대해 다음 과정을 반복합니다.

  • 예시 1: 사람의 머리 부분 픽셀 $(i_{head}, j_{head})$

    • 이 픽셀 위치에서 3개의 업샘플링된 제안 맵의 값을 확인합니다.
    • $\bar{L}_p[1, i_{head}, j_{head}]$ (사람 제안의 활성화 값)
    • $\bar{L}_p[2, i_{head}, j_{head}]$ (자동차 제안의 활성화 값)
    • $\bar{L}_p[3, i_{head}, j_{head}]$ (하늘 제안의 활성화 값)
    • 이 픽셀은 사람 머리 부분에 해당하므로, 사람 제안 맵($\bar{L}_p[1, :, :]$)이 이 위치에서 다른 제안 맵보다 훨씬 높은 값을 가질 가능성이 높습니다.
    • 즉, $\bar{L}_p[1, i_{head}, j_{head}]$ 값이 세 값 중에서 가장 클 것입니다.
    • 따라서 픽셀 $(i_{head}, j_{head})$의 최종 세그멘테이션 레이블은 가장 높은 값을 가진 제안의 인덱스인 1이 됩니다. ($S[i_{head}, j_{head}] = 1$)

  • 예시 2: 자동차의 문 부분 픽셀 $(i_{car}, j_{car})$

    • 이 픽셀 위치에서 3개의 업샘플링된 제안 맵의 값을 확인합니다.
    • $\bar{L}_p[1, i_{car}, j_{car}]$ (사람 제안의 활성화 값)
    • $\bar{L}_p[2, i_{car}, j_{car}]$ (자동차 제안의 활성화 값)
    • $\bar{L}_p[3, i_{car}, j_{car}]$ (하늘 제안의 활성화 값)
    • 이 픽셀은 자동차 문 부분에 해당하므로, 자동차 제안 맵($\bar{L}_p[2, :, :]$)이 이 위치에서 가장 높은 값을 가질 가능성이 높습니다.
    • 따라서 픽셀 $(i_{car}, j_{car})$의 최종 세그멘테이션 레이블은 2가 됩니다. ($S[i_{car}, j_{car}] = 2$)

  • 예시 3: 하늘 영역 부분 픽셀 $(i_{sky}, j_{sky})$

    • 이 픽셀 위치에서 3개의 업샘플링된 제안 맵의 값을 확인합니다.
    • $\bar{L}_p[1, i_{sky}, j_{sky}]$ (사람 제안의 활성화 값)
    • $\bar{L}_p[2, i_{sky}, j_{sky}]$ (자동차 제안의 활성화 값)
    • $\bar{L}_p[3, i_{sky}, j_{sky}]$ (하늘 제안의 활성화 값)
    • 이 픽셀은 하늘 영역에 해당하므로, 하늘 제안 맵($\bar{L}_p[3, :, :]$)이 이 위치에서 가장 높은 값을 가질 가능성이 높습니다.
    • 따라서 픽셀 $(i_{sky}, j_{sky})$의 최종 세그멘테이션 레이블은 3이 됩니다. ($S[i_{sky}, j_{sky}] = 3$)

이 과정을 이미지의 모든 픽셀에 대해 반복합니다.

• 결과:
  • 모든 픽셀이 가장 활성화가 강했던 제안의 인덱스(이 예시에서는 1, 2, 또는 3)로 레이블링된 512x512 크기의 최종 세그멘테이션 마스크 $S$가 생성됩니다.
  • 이 마스크는 이미지 내의 사람, 자동차, 하늘 영역을 서로 겹치지 않는 픽셀 그룹으로 분할한 결과가 됩니다.

NMS는 여러 객체 제안들 중에서 각 픽셀을 어느 제안에 할당할지 결정하는 간단하지만 효과적인 방법입니다. 각 제안이 특정 객체/영역을 나타내는 확률 맵이라고 볼 때, NMS는 각 픽셀에서 가장 높은 확률을 보인 제안을 해당 픽셀의 최종 소속으로 결정하는 역할을 합니다.