Abstract

Fig. 1

• 문제 인식: Keypoint 및 Landmark 검출 분야에서 최신 신경망 아키텍처 덕분에 비지도 학습 방식에 상당한 발전이 있었지만, 아직까지 성능 면에서 지도 학습 방식에 미치지 못하여 실용성에 의문이 있었습니다. 특히 기존 비지도 학습 방법은 데이터 전처리가 되지 않거나 객체의 Ground Truth 위치를 알아야 하는 등의 제약이 있었습니다.

• 제안하는 방법: 저자들은 Text-to-Image Diffusion 모델, 특히 High-resolution image synthesis with latent diffusion models과 같은 대규모 사전 학습 모델에 내재된 지식을 활용하여 더 강건한 비지도 Keypoint를 얻는 방법을 제안합니다.

• 핵심 아이디어:

  • 연구자들은 Cross-Attention 메커니즘을 역으로 활용합니다. 이미지를 생성하기 위해 텍스트를 사용하는 대신, 주어진 이미지에 대해 특정 위치에 대응하는 Text Embedding을 찾아내는 것입니다.
  • 즉, 어떤 Text Embedding은 개 이미지 모음에서 항상 개의 "코" 부분에 강하게 주의를 기울이도록 학습될 수 있습니다. 또 다른 Text Embedding은 항상 개의 "왼쪽 귀" 부분에 주의를 기울이도록 학습될 수 있습니다.
  • 이렇게 특정 이미지 영역에 일관적으로(Consistently) 주의를 기울이는 Text Embedding을 찾으면, 이 Text Embedding 자체가 그 영역을 나타내는 "Keypoint" 역할을 하게 됩니다. 여러 이미지에서 동일한 의미적 위치(예: 얼굴의 왼쪽 눈)를 찾을 수 있는 기준점이 되는 것이죠.

방법론

간단히 Text Embedding을 최적화하여 Denoising 네트워크 내의 Cross-Attention 맵이 표준 편차가 작은 Gaussian과 같이 국지화되도록 합니다.

• 최적화(Optimization)

  • 이전 단계에서 목표를 "Text Embedding을 찾는 것"이라고 했습니다. 최적화는 이 Text Embedding의 숫자 값을 조금씩 조정해 나가면서 원하는 목표(Keypoint를 잘 나타내는 것)를 달성하는 과정입니다.
  • 연구자들은 처음에 무작위로 초기화된 Text Embedding에서 시작합니다. 그리고 이 Embedding을 사용하여 이미지에 대한 Cross-Attention 맵을 계산합니다.

• Cross-Attention 맵의 '국지화(Localization)'

  • Cross-Attention 맵은 이미지와 같은 형태의 2D 그리드로 상상할 수 있습니다. 각 셀의 값은 해당 Text Token이 이미지의 그 위치에 얼마나 강하게 주의를 기울이는지를 나타냅니다.
  • '국지화'된다는 것은 주의가 이미지의 넓은 영역에 퍼져 있지 않고, 하나의 작은 영역에 집중된다는 의미입니다. Keypoint는 이미지의 특정 '점' 또는 아주 작은 영역을 나타내므로, Attention 맵이 넓게 퍼져 있다면 Keypoint를 정확히 찾기 어렵습니다.

• 표준 편차가 작은 Gaussian과 같이 만들라는 의미

  • Gaussian 분포(가우시안 함수)는 중앙값이 가장 높고 중앙에서 멀어질수록 값이 부드럽게 감소하는 종 모양의 곡선입니다. 2D 이미지에서는 중앙에서 가장 높은 봉우리를 가지고 주변으로 갈수록 낮아지는 형태가 됩니다.
  • '표준 편차(Standard Deviation)'는 이 분포가 얼마나 퍼져 있는지를 나타냅니다. 표준 편차가 작으면 봉우리가 뾰족하고 폭이 좁아서 주의가 중앙에 강하게 집중됩니다. 표준 편차가 크면 봉우리가 완만하고 폭이 넓어서 주의가 넓게 퍼집니다.
  • 따라서 Cross-Attention 맵이 '표준 편차가 작은 Gaussian과 같이 국지화'되도록 한다는 것은, Text Embedding에 해당하는 Attention 맵이 이미지의 어떤 한 지점에서 가장 높은 값을 가지고, 그 지점에서 멀어질수록 값이 빠르게 감소하여 마치 뾰족한 봉우리처럼 보이도록 만들라는 의미입니다.

• 최적화 목표 설정:

  • 연구자들은 Text Embedding을 최적화하는 과정에서, 각 Text Token에 해당하는 Attention 맵이 가장 높은 값을 가지는 지점을 찾습니다.
  • 그리고 이 지점을 중심으로 하는 '이상적인' Gaussian 분포를 만듭니다 (표준 편차는 작게 설정).
  • 그 후, 실제 Cross-Attention 맵이 이상적인 Gaussian 분포와 유사해지도록 Text Embedding의 값을 조정합니다. 이 유사성을 측정하는 방법으로 두 맵의 차이의 제곱 합(L2 손실)을 사용합니다 ($\| \tilde{M}_n - G_n \|^2$). 논문에서는 이를 Llocalize 손실이라고 부릅니다 (수식 (6) 참고).
  • 이 손실 값이 최소화되도록 Text Embedding을 반복적으로 업데이트합니다.

• 결과:

  • 이 최적화 과정을 거치면, 각 무작위 Text Embedding은 데이터셋의 여러 이미지에서 특정 의미적 위치에 일관적으로 국지화된 Attention 맵을 생성하도록 학습됩니다.
  • 이렇게 학습된 Text Embedding이 Keypoint를 나타내게 되며, 해당 Attention 맵에서 가장 높은 값이 나타나는 위치를 Keypoint의 최종 위치로 사용합니다.

1. Introduction

• Keypoint의 중요성

  • Keypoint는 이미지 매칭, 3D 복원, 모션 트래킹 등 다양한 컴퓨터 비전 작업에 필수적입니다.
  • 많은 컴퓨터 비전 문제와 마찬가지로, Keypoint 탐지 연구에서도 지도 학습이 널리 사용되었습니다.
  • 하지만 지도 학습은 데이터 레이블링이 매우 번거롭고, 얼굴 Keypoint처럼 중요한 위치를 일관성 있게 정의하기 어려운 모호함이 있습니다.
  • 이러한 어려움 때문에 비지도 학습 접근 방식이 연구되어 왔습니다. 기존 비지도 방법들은 주로 오토인코더 기반이거나, Keypoint 위치의 공간적 지역성 및 변형에 대한 일관성을 강제하는 손실 함수를 사용했습니다.
  • 하지만 이러한 기존 방법들은 미리 전처리되지 않은 데이터에 취약하고, 객체의 실제 위치에 의존하는 경향이 있어 실용적인 적용에 제한이 있음을 지적합니다.

• Stable Diffusion을 이용한 비지도학습 기반 Keypoint 추출

  • 주요 아이디어는 특정 객체 클래스의 이미지에서 일관적으로 구별되는 위치에 해당하는 텍스트 임베딩(text embeddings)을 찾는 것을 통해 "중요한" Keypoint를 지역화하는 것입니다.

  • 이 아이디어는 심지어 무작위 텍스트 임베딩을 사용하더라도, 다양한 이미지에 대한 어텐션 맵(attention maps)이 의미론적으로 유사한 영역에 대략적으로 일관되게 반응한다는 관찰(Fig. 1 참조)에 근거합니다.

  • 따라서 텍스트 임베딩이 의미론적 의미를 내포하고 있으며, 이것이 이미지 컬렉션을 서로 연관시키는 데 사용될 수 있음을 Fig. 2를 통해 보여줍니다.
    

• 방법론

  • Stable Diffusion의 교차 어텐션(cross-attention) 레이어에서 국소적으로 반응하는 텍스트 임베딩 내의 토큰(tokens) 세트를 찾도록 최적화합니다.

  • 지역성은 각 토큰의 어텐션 반응이 단일 모드 가우시안 분포(single-mode Gaussian distribution)와 유사하도록 최대화함으로써 강제됩니다.

  • Stable Diffusion 내에서 교차 어텐션 레이어가 구성되는 방식 덕분에, 이 간단한 목표만으로도 다른 토큰들이 이미지의 동일한 위치에 집중하는 것을 자연스럽게 방지할 수 있습니다.

  • 제안된 방법은 CelebA, CUB-200-2011, Tai-Chi-HD, DeepFashion, Human3.6m 등 여러 데이터셋에서 평가되었습니다.

  • 정제되고 잘 정렬된 데이터셋에서는 최신 기술(state-of-the-art)과 동등한 결과를 보여줍니다.

  • 반면, 특히 정렬되지 않고 덜 정제된 데이터(in-the-wild setup)에서는 성능이 크게 향상되었으며, 경우에 따라서는 완전 지도 학습 기준선(fully supervised baselines)을 능가하는 결과도 달성했음을 밝힙니다.

2. Related Works

지도 학습 기반 키포인트 연구 (Learning keypoints with supervision):

• 포즈 추정(Pose estimation), 랜드마크 추정(Landmark estimation) 등 다양한 컴퓨터 비전 문제에서 중요하게 활용됩니다.

• Part Affinity Fields, 시공간 일관성(temporal consistency), 공간 관계(spacial relationships), 기하학적 제약(geometry constraints) 등 다양한 기술이 사용됩니다.

• 한계점: 성공적인 결과를 얻기 위해서는 대규모의 고품질 레이블링된 데이터셋이 필수적이지만, 데이터 수집 및 레이블링 과정이 매우 어렵고 비용이 많이 듭니다. 특정 객체 범주에 대해 광범위하고 세심하게 주석이 달린 데이터를 확보하는 것은 확장성 측면에서 큰 단점입니다.

자기 지도 학습 기반 키포인트 연구 (Learning keypoints via self-supervision):

• 레이블링되지 않은 대규모 데이터를 활용하려는 시도입니다.

• 주로 이미지 변화에 따른 키포인트의 움직임을 추적하거나, 알려진 변환에 대한 다양한 제약 조건을 활용합니다.

• 일부 방법은 GAN 또는 오토인코더를 사용하여 이미지 재구성을 통해 키포인트를 학습하기도 합니다.

• 한계점: 배경 모델링(background modeling)이나 자세 변화(pose variations)에 어려움을 겪는 경우가 많습니다. GAN 기반 방법은 학습 불안정성이 있을 수 있으며, 오토인코더 기반 방법은 각 데이터셋에 대해 처음부터 다시 학습해야 하는 단점이 있습니다. 본 논문의 방법은 이러한 GAN 불안정성이나 데이터셋별 미세 조정이 필요 없습니다.

확산 모델의 이미지 이해 능력 활용 (Diffusion models for image understanding):

• 최근 Stable Diffusion과 같은 대규모 텍스트-이미지 확산 모델들이 뛰어난 이미지 생성 품질을 보여주며 주목받고 있습니다.

• 이러한 모델들은 사전 학습 과정에서 이미지의 잠재 공간(latent space)에 실제 이미지에 대한 강력한 사전 정보(priors)를 학습합니다.

• 별도의 재학습 없이도 이미지 대응(image correspondence), 객체 탐지(object detection), 의미론적 분할(semantic segmentation), 이미지 분류(image classification) 등 다양한 하위 비전 작업에서 놀라운 능력을 보여주었습니다. Null-text Inversion for Editing Real Images using Guided Diffusion Models 등의 연구는 확산 모델의 cross-attention 맵이 텍스트 토큰과 의미론적으로 관련된 영역을 연결함을 발견했습니다.

확산 모델을 통한 대응 추정 (Correspondences via diffusion models):

• 확산 모델의 잠재된 능력을 활용하여 이미지 간 대응(correspondence)을 추정하는 연구들이 진행되었습니다.

• 예를 들어, Unsupervised Semantic Correspondence Using Stable Diffusion 연구는 원본 이미지의 특정 지점에 대한 주의 맵(attention map)을 최적화하여 대상 이미지에서의 대응되는 활성화를 찾습니다.

• 본 논문의 차별점: 본 논문의 방법은 이러한 주의 맵 활용 아이디어는 공유하지만, 단일 이미지가 아닌 특정 객체 클래스의 이미지 데이터셋을 기반으로 임베딩을 최적화합니다. 즉, 사용자의 입력 없이도 데이터셋 내의 모든 이미지에 걸쳐 의미론적으로 대응되는 위치(키포인트)를 스스로 발견하는 데 중점을 둡니다.

3. Method

• 목표: 이미지 데이터셋에서 대표적인 키포인트를 비지도 학습 방식으로 식별하는 것입니다. 이는 사람이 직접 키포인트 위치를 지정해주는 레이블링 과정 없이 이루어집니다.

• 핵심 아이디어: 사전 학습된 조건부 확산 모델, 특히 Stable Diffusion과 같은 Latent Diffusion Model의 크로스 어텐션 맵(cross-attention maps)을 활용합니다.

• 방법: 이 논문은 텍스트 임베딩(text embeddings)과 이미지 피처(image features) 사이의 크로스 어텐션 맵이 이미지 내의 매우 국지적인 영역(highly localized regions)에 일관되게 집중하도록 학습합니다. 즉, 특정 텍스트 임베딩이 데이터셋 내 다양한 이미지에서 동일한 특정 위치(키포인트)에 반응하도록 만듭니다.

• 이전 연구와의 차별점: 이전 연구인 Unsupervised Semantic Correspondence Using Stable Diffusion가 이미 주어진 특정 키포인트 위치에 대한 대응점을 다른 이미지에서 찾는 방식이었다면, 이 논문은 어떤 위치에 집중해야 하는지에 대한 사전 정보 없이 데이터셋 내의 모든 이미지에서 의미론적 대응점(semantic correspondences)을 스스로 발견합니다.

• 가능하게 하는 요소: 이러한 비지도 키포인트 식별은 주로 국지성(locality)과 변환 불변성(equivariance)을 강제하는 학습 과정을 통해 달성됩니다. 국지성은 어텐션 맵이 좁은 영역에 집중하게 하고, 변환 불변성은 이미지의 변환(예: 회전, 확대/축소)에도 키포인트가 동일한 의미 있는 위치에 유지되도록 합니다.

3.1 Attention maps in diffusion networks

확산모델

• 확산 모델의 기본 원리:

  • 확산 모델은 점진적으로 노이즈를 제거하는 방식으로 데이터를 생성하는 모델입니다.
  • 기본 아이디어는 데이터 분포(예: 실제 이미지)를 잡음 분포(예: 가우시안 노이즈)로 점진적으로 변환하는 "순방향 확산 과정(forward diffusion process)"과, 이 과정을 역으로 되돌려 잡음에서 데이터를 복원하는 "역방향 잡음 제거 과정(inverse denoising process)"을 학습하는 것입니다.

• 잠재 공간 확산 모델 (Latent Diffusion Model):

  • 고해상도 이미지 자체에 바로 확산 과정을 적용하는 대신, 이미지를 압축된 잠재 표현(latent representation) $z$ 로 변환하여 이 잠재 공간에서 확산 과정을 수행합니다. 이는 계산 효율성을 높여줍니다.
  • 이미지 $X$는 인코더에 의해 잠재 공간의 $z$로 변환되고, $z$는 디코더에 의해 다시 이미지 $X$로 복원됩니다.

• 조건부 확산 모델 (Conditional Diffusion Models):

  • 특정 조건(예: 텍스트 설명)에 따라 이미지를 생성하기 위해 사용되는 확산 모델입니다.
  • 여기서는 텍스트 조건 $y$가 텍스트 임베딩(text embedding) $e = \tau_\theta(y)$ 형태로 변환되어 잡음 제거 네트워크(denoiser)에 입력됩니다.
  • 모델은 이 텍스트 임베딩 $e$를 활용하여 잠재 표현 $z_t$에 추가된 노이즈 $\epsilon$를 예측하는 $\epsilon_\theta(z_t, t, e)$를 학습합니다.

• 모델 학습 목표 (손실 함수):

  • 조건부 확산 모델은 다음 손실 함수를 최소화하도록 학습됩니다.

    $L_{LDM} = E_{z,t,\epsilon \sim N(0,1)}\left[\left\|\epsilon - \epsilon_\theta(z_t, t, e)\right\|^2_2\right] \quad (1)$

  • 이 손실 함수는 예측된 노이즈 $\epsilon_\theta(z_t, t, e)$가 실제 추가된 노이즈 $\epsilon$와 얼마나 차이가 나는지를 측정합니다. 각 항의 의미는 다음과 같습니다.

    • $E_{z,t,\epsilon \sim N(0,1)}[\cdot]$: 잠재 표현 $z$, 시간 단계 $t$, 그리고 표준 가우시안 분포 $N(0,1)$에서 샘플링된 노이즈 $\epsilon$에 대한 기댓값입니다. 즉, 다양한 입력과 노이즈에 대해 평균적인 성능을 높이겠다는 의미입니다.

    • $\epsilon$: 실제 시간 단계 $t$에서 잠재 표현 $z_t$에 더해진 노이즈입니다.

    • $\epsilon_\theta(z_t, t, e)$: 학습 가능한 모델 $\theta$ (잡음 제거 네트워크)가 현재 잠재 표현 $z_t$, 시간 단계 $t$, 그리고 텍스트 임베딩 $e$를 입력받아 예측한 노이즈입니다.

    • $\|\cdot\|^2_2$: L2 Norm으로, 실제 노이즈와 모델이 예측한 노이즈 간의 차이(오차)를 계산합니다.

    • 손실 함수는 이 오차를 최소화하여 모델이 노이즈를 정확하게 예측하고, 이를 통해 원본 잠재 표현 $z$를 잘 복원할 수 있도록 학습시킵니다.

• 잡음 제거 네트워크 (Denoiser) 구조:

  • 잡음 제거 네트워크 $\epsilon_\theta(z_t, t, e)$는 일반적으로 트랜스포머(transformer) 구조를 기반으로 하며, 셀프 어텐션(self-attention) 레이어와 크로스 어텐션(cross-attention) 레이어의 조합으로 구성됩니다.

  • 크로스 어텐션 레이어는 특히 텍스트 임베딩 $e$와 잠재 표현 $z_t$ 사이의 관계를 연결하는 역할을 합니다. 이 논문의 핵심 아이디어는 바로 이 크로스 어텐션 맵을 활용하여 이미지의 특징점(keypoint)을 찾는 것입니다.

기댓값 $E_{z,t,\epsilon \sim N(0,1)}[\cdot]$의 구현 방법

기댓값 $E[\cdot]$은 확률 분포에 대한 평균값을 의미합니다. 이 논문의 손실 함수에서는 잠재 표현 $z$, 시간 단계 $t$, 표준 가우시안 노이즈 $\epsilon$에 대한 평균을 구해야 합니다. 실제 딥러닝 학습 과정에서는 이 기댓값을 수학적으로 정확하게 계산하기 어렵기 때문에, 몬테카를로 근사(Monte Carlo approximation)라는 방법을 사용합니다. 이는 간단히 말해, 분포로부터 여러 샘플을 뽑아서 함수 값을 계산한 뒤, 그 평균을 내는 방식입니다.

구체적인 구현 단계는 다음과 같습니다.

• 미니 배치 (Mini-batch) 사용: 딥러닝 학습에서는 보통 전체 데이터셋을 한 번에 처리하지 않고, 작은 묶음인 '미니 배치' 단위로 데이터를 사용합니다. 기댓값의 근사는 이 미니 배치 내의 샘플들에 대한 평균으로 이루어집니다.

• 샘플링 과정: 한 번의 학습 반복(iteration) 동안, 미니 배치에 포함된 각 샘플에 대해 다음 과정을 수행합니다.

  1. 이미지 샘플링 ($z$): 학습 데이터셋에서 이미지 $X$들을 미니 배치 크기만큼 무작위로 추출합니다. 이 이미지들은 인코더를 통해 시간 단계 0의 잠재 표현 $z_0$으로 변환됩니다. (이 논문에서는 $z_0$가 아닌 시간 단계 $t$에서의 잠재 표현 $z_t$를 사용하는데, $z_t$는 $z_0$와 $\epsilon$로부터 결정됩니다. 여기서는 $z_0$를 데이터로부터 얻는 시작점으로 이해하시면 됩니다.)

  2. 시간 단계 샘플링 ($t$): 확산 과정의 전체 시간 단계 $T$ (논문에서 $T=50$을 언급) 중 하나의 시간 단계 $t$를 무작위로 선택합니다. 일반적으로 $1$부터 $T$ 사이에서 균일하게 샘플링됩니다.

  3. 노이즈 샘플링 ($\epsilon$): 표준 가우시안 분포 $N(0,1)$에서 노이즈 벡터 $\epsilon$를 무작위로 샘플링합니다. 이 노이즈는 $z_0$에 시간 단계 $t$에 해당하는 양만큼 더해져 $z_t$를 만드는데 사용됩니다. (수학적으로 $z_t$는 $z_0$, $t$, $\epsilon$의 함수입니다.)

• 손실 계산 및 평균:

  • 샘플링된 $z_t$와 $t$, 그리고 텍스트 임베딩 $e$를 잡음 제거 네트워크 $\epsilon_\theta$에 입력하여 예측된 노이즈 $\epsilon_\theta(z_t, t, e)$를 얻습니다.

  • 샘플링된 실제 노이즈 $\epsilon$와 예측된 노이즈 $\epsilon_\theta(z_t, t, e)$ 사이의 차이인 $\epsilon - \epsilon_\theta(z_t, t, e)$를 계산합니다.

  • 이 차이 벡터의 제곱 L2 Norm (Squared L2 Norm)인 $\|\epsilon - \epsilon_\theta(z_t, t, e)\|^2_2$를 계산합니다.

  • 미니 배치에 포함된 모든 샘플에 대해 이 과정을 반복하고, 계산된 $\|\cdot\|^2_2$ 값들의 평균을 구합니다. 이 평균값이 기댓값 $E_{z,t,\epsilon \sim N(0,1)}[\cdot]$에 대한 근사치가 됩니다.

• 모델 파라미터 업데이트: 계산된 평균 손실 값에 대해 모델 파라미터 $\theta$ (잡음 제거 네트워크의 가중치 등)에 대한 그래디언트를 계산하고, 옵티마이저(예: Adam)를 사용하여 파라미터를 업데이트합니다.

크로스 어텐션

크로스 어텐션(Cross-Attention)의 역할

확산 모델은 종종 텍스트와 같은 추가 정보(조건, condition)에 기반하여 이미지를 생성합니다. 크로스 어텐션 메커니즘은 이러한 조건 정보(여기서는 텍스트 임베딩 $e$)와 이미지 특징($z_t$)을 연결하여, 텍스트의 특정 부분이 이미지의 어느 영역에 해당하는지 모델이 이해하도록 돕습니다. 어텐션 메커니즘은 기본적으로 Query와 Key의 유사성을 계산하여 가중치를 부여합니다.

Query

• Query ($Q^c_l$)는 이미지 특징 $z_t$로부터 생성됩니다. 구체적으로, U-Net의 $l$-번째 레이어와 $c$-번째 어텐션 헤드에서 $\Phi^c_l(z_{t=1})$ 함수를 통해 계산됩니다. 그 형태는 $R^{(H \times W) \times D_l}$이며, 이는 이미지의 공간 해상도 $(H \times W)$와 레이어의 차원 $D_l$을 의미합니다.

• U-Net은 여러 개의 Convolutional 및 Transformer 레이어로 구성되어 있습니다. 이 중 모든 레이어에서 크로스 어텐션을 수행하는 것은 아니고, 논문에서 언급된 것처럼 특정 레이어들 (예: 7~10번째 레이어)에서 주로 수행됩니다.

  • Transformer 레이어 내부에는 여러 개의 독립적인 어텐션 헤드가 병렬로 작동합니다 (예: $C$개). 각 헤드는 입력에 대해 서로 다른 변환을 적용하고 독자적인 어텐션 결과를 계산합니다.
  • $Q^c_l$은 $l$-번째 레이어의 $c$-번째 어텐션 헤드를 위한 쿼리를 의미하므로, 크로스 어텐션이 있는 각 레이어 $l$마다 헤드 수 $C$개만큼의 서로 다른 쿼리 $Q^c_l$이 존재하게 됩니다.
  • 이후 아래의 식 (2)에서처럼 한 레이어 내의 모든 헤드($c=1, \dots, C$)의 어텐션 결과를 평균하여 해당 레이어의 최종 어텐션 맵 $M_l$을 얻고, 식 (3)에서처럼 다시 여러 레이어의 $M_l$을 평균하여 최종 맵 $\tilde{M}$을 얻습니다. 즉, 계산 과정에서는 각 $Q^c_l$이 사용되지만, 최종적으로 우리가 사용하는 정보는 이러한 개별 쿼리들의 결과가 종합된 형태입니다.

• $\Phi^c_l(z_{t=1})$는 입력 이미지 특징 $z_{t=1}$을 $l$-번째 레이어의 $c$-번째 어텐션 헤드에서 사용할 Query ($Q^c_l$)로 변환하는 함수입니다.

  • 딥러닝 모델에서 함수 표기 $\Phi(\cdot)$는 일반적으로 특정 연산 블록이나 변환 과정을 나타냅니다. 어텐션 메커니즘에서는 Query, Key, Value를 만들기 위해 입력 특징에 대한 학습 가능한 선형 변환(가중치 행렬 곱)을 사용합니다.
  • 따라서 $\Phi^c_l$ 함수는 $z_{t=1}$의 형태를 크로스 어텐션 계산에 적합한 Query의 형태($R^{(H \times W) \times D_l}$)로 바꾸는 역할을 합니다. 이 변환은 $l$-번째 레이어의 $c$-번째 헤드에 특화되어 학습된 가중치를 사용합니다.
  • 저자들은 $T=50$ 일 때 $t=1$의 상태를 차용한다고 합니다.

• $H$, $W$, $D_l$ 기호들은 U-Net 아키텍처의 중간 단계에서 처리되는 이미지 특징 맵의 크기와 차원을 나타냅니다.

  • $H$와 $W$: U-Net은 다운샘플링(이미지 크기 축소)과 업샘플링(이미지 크기 복원) 과정을 거치기 때문에, 초기 입력 이미지의 해상도와는 다를 수 있습니다. 따라서 $\Phi^c_l(z_{t=1})$ 함수를 통해 이를 원본 이미지 해상도 $H \times W$로 맞춰주는 것입니다.

  • $D_l$: 컬러 이미지는 보통 3개의 채널(RGB)을 가지지만, 신경망의 중간 레이어에서는 수십 또는 수백 개의 채널을 가질 수 있으며, 이 채널들은 이미지의 다양한 특징(엣지, 텍스처, 패턴 등)을 인코딩합니다. 이 또한 $\Phi^c_l(z_{t=1})$에 의해 일정한 크기의 차원 $D_l$으로 변환됩니다.

  • Query $Q^c_l$의 형태가 $R^{(H \times W) \times D_l}$인 것은, 특징 맵의 각 공간 위치 $H \times W$에 대해 $D_l$ 차원의 Query 벡터가 계산된다는 것을 보여줍니다.

Key

• Key ($K^c_l$)는 텍스트 임베딩 $e$로부터 생성됩니다. $\Psi^c_l(e)$ 함수를 통해 계산되며, 형태는 $R^{N \times D_l}$입니다. 여기서 $N$은 텍스트 토큰의 수입니다.

• 텍스트 임베딩 $e$

  • 텍스트 입력 ($y$): 먼저 사용자가 입력하는 텍스트 설명문(예: "파란 눈을 가진 고양이")이 있습니다. 이것이 텍스트 $y$입니다.

  • 텍스트 인코더 ($\tau_\theta$): 이 텍스트 $y$는 '텍스트 인코더'라고 불리는 별도의 신경망 모델 $\tau_\theta$를 통과합니다. $\tau_\theta$는 미리 학습되어 있으며, 텍스트의 의미론적 정보를 파악하여 이를 벡터 형태로 변환하는 역할을 합니다. Stable Diffusion과 같은 모델에서는 CLIP 모델의 텍스트 인코더가 자주 사용됩니다.

  • 텍스트 임베딩 ($e$): $\tau_\theta$의 출력이 바로 텍스트 임베딩 $e$입니다. 이 $e$는 입력 텍스트 $y$의 의미를 압축하여 담고 있는 수치적 표현(벡터 또는 벡터의 시퀀스)입니다. 이 임베딩 $e$가 확산 모델의 denoiser 부분으로 전달되어 이미지 생성 과정에 영향을 미칩니다.

    즉, 텍스트 임베딩 $e$는 입력 텍스트를 텍스트 인코더라는 별도의 모델을 거쳐 얻어지는 의미론적 벡터 표현입니다.

• $\Psi^c_l(e)$ 함수

  • 텍스트 임베딩 $e$를 $l$-번째 레이어의 $c$-번째 어텐션 헤드에서 사용할 Key ($K^c_l$)로 변환하는 함수입니다.

  • 트랜스포머 어텐션 메커니즘의 핵심은 Query, Key, Value라는 세 가지 표현을 사용하는 것입니다. Query와 Key 사이의 유사성을 계산하여 Value의 정보를 얼마나 가져올지 결정합니다.

  • Key $K^c_l$는 텍스트 임베딩 $e$로부터 생성됩니다. $\Psi^c_l(\cdot)$ 함수는 이 텍스트 임베딩 $e$를 입력으로 받아, 이미지 Query $Q^c_l$와 비교될 수 있는 형태의 Key $K^c_l$로 변환합니다.

  • 이 함수 역시 $\Phi^c_l(\cdot)$와 유사하게 학습 가능한 선형 변환(가중치 행렬 곱)을 포함하며, 어텐션 헤드의 구조에 따라 추가적인 연산이 있을 수 있습니다. 헤드마다 다른 $\Psi^c_l$ 함수를 사용하여 텍스트 임베딩의 다양한 측면을 포착하고 Key로 변환합니다.

• $R^{N \times D_l}$ 형태를 가지는 이유

  • 이는 Query와 Key의 내적 계산을 위해 차원을 일치시켜야 하기 때문입니다.

  • $N$: 텍스트 임베딩$e$는 일반적으로 입력 텍스트를 여러 개의 '토큰'으로 분해한 후, 각 토큰에 대한 임베딩 벡터를 얻어 연결한 형태입니다.$N$은 이 텍스트 임베딩에 포함된 토큰의 총 개수입니다. 예를 들어 "a blue cat" 이라는 텍스트가 있다면, 'a', 'blue', 'cat' 각각이 하나의 토큰이 되어$N=3$이 될 수 있습니다.

  • $D_l$: $D_l$은 앞서 설명했듯$l$-번째 U-Net 레이어의 이미지 특징 맵이 가지는 채널 차원입니다. 그리고 Query $Q^c_l$의 형태가$(H \times W) \times D_l$이었습니다.

  • 차원 일치의 필요성: 크로스 어텐션의 핵심인 Query와 Key의 유사성 계산 ($Q^c_l \cdot K^c_l$)은 내적(dot product) 형태를 사용합니다. 행렬 내적을 수행하려면 첫 번째 행렬의 열 수와 두 번째 행렬의 행 수가 일치해야 합니다.

    • $Q^c_l$의 형태는$(H \times W) \times D_l$입니다. 이는$(H \times W)$개의 행과$D_l$개의 열을 가진 행렬로 생각할 수 있습니다.

    • $K^c_l$의 형태는$N \times D_l$입니다.

    • 어텐션 계산에서는 $Q^c_l$와 $K^c_l$의 '전치(transpose)' 행렬을 곱합니다. $K^c_l$의 전치는 $D_l \times N$형태가 됩니다.

    • 따라서$Q^c_l \cdot (K^c_l)^T$를 계산하면, 형태는$((H \times W) \times D_l) \cdot (D_l \times N)$이 되어 결과 행렬의 형태는$(H \times W) \times N$이 됩니다. 이것이 바로 식 (2)의 softmax 연산 전 형태인 $Q^c_l \cdot K^c_l$의 형태이며, 각 이미지 공간 위치($(H \times W)$중 하나)가 각 텍스트 토큰($N$중 하나)과 얼마나 관련 있는지 ($D_l$차원 공간에서의 유사성)를 나타냅니다.

    결론적으로,$\Psi^c_l$함수는 텍스트 임베딩$e$의 원래 차원($D_{text}$라고 가정)을 이미지 Query$Q^c_l$의 마지막 차원인$D_l$과 동일하게 '투영(project)'시켜주는 역할을 합니다. 이를 통해 이미지 특징(Query)과 텍스트 특징(Key)이 같은$D_l$차원 공간에서 비교될 수 있게 되는 것입니다.$D_l$은 해당 레이어의 이미지 특징 차원에 맞춰져 있으며, 텍스트 Key도 이 차원으로 변환되는 것입니다.

크로스 어텐션 맵 계산

크로스 어텐션 맵 $M_l$은 다음 수식을 통해 계산됩니다.

• $Q^c_l \cdot K^c_l$: Query와 Key의 행렬 곱입니다. 이는 이미지의 각 공간 위치가 각 텍스트 토큰과 얼마나 관련 있는지(유사성)를 나타내는 행렬 $R^{(H \times W) \times N}$을 생성합니다.

• $\frac{Q^c_l \cdot K^c_l}{\sqrt{D_l}}$: 안정적인 학습을 위해 내적 결과에 스케일링 인자 $\sqrt{D_l}$를 나눕니다.

• $\text{softmax}_n(\cdot)$: 스케일링된 유사성 값에 소프트맥스 함수를 적용합니다. 이 소프트맥스는 텍스트 토큰 차원($N$)을 따라 적용되어, 이미지의 각 공간 위치가 N개의 토큰 각각에 대해 얼마나 '주목'하는지에 대한 확률 분포를 만듭니다. 결과적으로 각 공간 위치에 대해 N개의 토큰에 대한 어텐션 가중치를 얻습니다.

• $E_c[\cdot]$: 여러 어텐션 헤드($C$개)에 걸쳐 계산된 어텐션 맵을 평균합니다. 이를 통해 각 헤드의 정보를 종합합니다. 이렇게 계산된 $M_l$은 형태가 $R^{(H \times W) \times N}$이며, $l$-번째 레이어에서 텍스트 토큰들이 이미지의 각 공간 위치에 얼마나 주목하는지를 보여줍니다.

다양한 레이어의 정보 결합

U-Net의 각기 다른 레이어는 이미지의 다양한 의미론적 수준을 포착합니다. 저자들은 여러 레이어(여기서는 7~10번째 레이어)의 어텐션 맵 정보를 결합하기 위해 평균 풀링을 사용합니다.

• $\tilde{M}$: 평균 풀링을 통해 얻은 최종 결합 어텐션 맵입니다.

• $E_{l=7..10}[\cdot]$: 선택된 레이어들($l=7$부터 $l=10$까지)의 어텐션 맵 $M_l$을 평균합니다.

• 이렇게 얻은 $\tilde{M}$ 맵은 텍스트 임베딩의 각 토큰($N$개)이 입력 이미지에서 어떤 공간 영역에 집중하는지에 대한 종합적인 정보를 담고 있습니다. 이 논문에서는 이 맵을 활용하여 비지도 학습 방식으로 키포인트를 찾습니다.

3.2 Optimizing to find the keypoint embeddings

확산 모델(Diffusion Model)의 텍스트 임베딩을 최적화하여 이미지에서 일관된 키포인트(keypoints)를 찾도록 학습하는 방법입니다. 이 방법은 크게 두 가지 목표를 달성하기 위한 손실 함수(loss function)를 사용하여 텍스트 임베딩을 조정합니다.

• 전체 손실 ($L_{total}$):
  이 논문에서 사용된 전체 손실 함수는 다음과 같이 두 가지 주요 손실 항의 합으로 정의됩니다.

  $L_{total} = L_{localize} + \lambda_{equiv}L_{equiv} \quad (4)$
  • $L_{total}$: 모델 학습에 사용되는 최종 손실 값입니다. 이 값을 최소화하는 방향으로 텍스트 임베딩이 최적화됩니다.
  • $L_{localize}$: 어텐션 맵(attention map)이 특정 영역에 집중되도록 유도하는 지역화(localization) 손실입니다.
  • $L_{equiv}$: 다양하게 변환된 이해 어텐션 맵이 일관성을 유지하도록 유도하는 동변성(equivariance) 손실입니다.
  • $\lambda_{equiv}$: 두 손실 항의 중요도 균형을 맞추기 위한 가중치입니다. 이 논문에서는 $\lambda_{equiv}=10$을 사용했다고 언급합니다.

• 동변성 손실 ($L_{equiv}$):
  이 손실은 입력 이미지 $X$에 기하학적 변환 $T$를 적용했을 때 (즉, $T(X)$), 변환된 이미지에서 계산된 어텐션 맵을 원래 이미지의 어텐션 맵과 비교하여 일관성을 강제합니다. 공식은 다음과 같습니다.

  $L_{equiv} = \mathbb{E}_n \left\|T^{-1}(M_n(e, T(X))) - M_n(e, X)\right\|^2 \quad (5)$

  • $\mathbb{E}_n$: 모든 텍스트 토큰 $n$에 대해 평균을 취한다는 의미입니다.

  • $M_n(e, X)$: 입력 이미지 $X$와 텍스트 임베딩 $e$에 대한 $n$번째 토큰의 어텐션 맵입니다.

  • $T(X)$: 입력 이미지 $X$에 기하학적 변환 $T$를 적용한 이미지입니다. 이 논문에서는 작은 어파인 변환(affine transformations)을 사용했으며, 구체적으로는 ±15도 회전, 이미지 너비의 ±0.25 범위 내에서의 이동, 그리고 원본 이미지 크기의 100-120% 스케일링을 적용했습니다.

  • $M_n(e, T(X))$: 변환된 이미지 $T(X)$에 대한 $n$번째 토큰의 어텐션 맵입니다.

  • $T^{-1}(\cdot)$: 변환된 이미지에서 얻은 어텐션 맵의 위치를 원래 이미지의 좌표계로 되돌리는 역변환입니다. 즉, 변환된 이미지에서의 키포인트 위치를 원래 이미지의 키포인트 위치로 역변환했을 때, 이 두 위치가 서로 일치하도록 만드는 역할을 합니다.

  • $\|\cdot\|^2$: 두 어텐션 맵 간의 차이(벡터)의 제곱 노름(L2 norm)입니다.

• 지역화 손실 ($L_{localize}$):
  이 손실은 각 텍스트 토큰에 해당하는 어텐션 맵 $\tilde{M}_n$이 이미지의 특정 한 영역에 집중되는 단일 모드 가우시안 분포(single-mode Gaussian distribution)와 유사해지도록 강제합니다. 공식은 다음과 같습니다.

  $L_{localize} = \mathbb{E}_n \left\|\tilde{M}_n - G_n\right\|^2 \quad (6)$

  • $\mathbb{E}_n$: 모든 텍스트 토큰 $n$에 대해 평균을 취한다는 의미입니다.

  • $\tilde{M}_n$: (3)번 공식에 의해 평균 계산을 거친 $n$번째 토큰의 어텐션 맵입니다.

  • $G_n$: $\tilde{M}_n$과 동일한 최대 응답 위치를 가지는 단일 모드 가우시안 분포 형태의 가상 이미지(Gaussian image)입니다. 이 손실은 실제 어텐션 맵 $\tilde{M}_n$이 목표 가우시안 이미지 $G_n$과 비슷해지도록 하여 어텐션이 특정 지점에 집중되게 만듭니다.

• 가우시안 타겟 ($G_n$) 생성:
  목표 가우시안 이미지 $G_n$은 다음과 같은 과정을 통해 생성됩니다.

  1. 먼저, $n$번째 토큰의 어텐션 맵 $\tilde{M}_n$에서 가장 큰 응답 값을 가지는 공간적 위치($\mu_n$)를 찾습니다.

     $\mu_n = \arg \max_{w,h} \tilde{M}_n[h, w] \quad (7)$

     • $\mu_n$: 어텐션 맵 $\tilde{M}_n$에서 최댓값을 가지는 픽셀의 $(h, w)$ 좌표입니다.

     • $\arg \max_{w,h} \tilde{M}_n[h, w]$: 어텐션 맵 $\tilde{M}_n$에서 높이 $h$와 너비 $w$ 방향으로 탐색하여 최댓값을 가지는 위치를 반환합니다.

  2. 찾은 위치 $\mu_n$을 중심으로 하는 가우시안 분포 형태의 이미지 $G_n$을 생성합니다.

     $G_n = \exp\left(-\frac{\|XY_{coord} - \mu_n\|^2}{2\sigma^2}\right) \quad (8)$

     • $G_n$: 생성된 목표 가우시안 이미지입니다.

     • $\exp(\cdot)$: 자연 상수 $e$의 지수 함수입니다.

     • $XY_{coord}$: 이미지 좌표를 나타내는 텐서입니다. 각 픽셀의 값은 해당 픽셀의 (x, y) 좌표입니다.

     • $\mu_n$: 가우시안 분포의 중심, 즉 최댓값 위치입니다.

     • $\|\cdot\|^2$: 유클리드 거리의 제곱입니다. 각 픽셀 좌표 $XY_{coord}$와 중심 $\mu_n$ 사이의 거리를 계산합니다.

     • $\sigma^2$: 가우시안 분포의 분산입니다. 이 값은 가우시안 분포의 퍼짐 정도를 결정하며, 키포인트의 '지역화' 정도를 조절하는 역할을 합니다. 이 논문에서는 작은 $\sigma$ 값을 사용하여 어텐션이 매우 좁은 영역에 집중되도록 유도합니다.

• 상호 배타성 촉진 (Promoting mutual exclusivity):

  • 문제: 여러 개의 텍스트 임베딩(토큰)이 이미지의 동일한 위치에 집중하려 할 수 있습니다. 이는 의미론적으로 구분되는 키포인트를 학습하는 데 방해가 됩니다.

  • 해결책: 저자들은 별도의 명시적인 제약 없이 국소화(localization) 손실(Llocalize)과 교차 어텐션 계산 시 사용되는 소프트맥스(softmax) 연산만으로 토큰들이 서로 다른 위치에 집중하도록 유도합니다.

  • 작동 방식:

    • 교차 어텐션 맵($\tilde{M}_n$)은 쿼리($Q^c_l$)와 키($K^c_l$)의 내적에 소프트맥스를 적용하여 계산됩니다 (식 2 참고). 여기서 키는 텍스트 임베딩($e$)에서 파생됩니다.

    • 만약 여러 개의 임베딩(토큰 $n$)이 서로 유사해지면, 해당 토큰들에 대한 키($K^c_l$)도 유사해집니다.

    • 이 경우, 소프트맥스 연산 결과인 어텐션 맵의 해당 토큰 차원 값들이 비슷해져서 특정 위치에 집중되지 않고 넓게 퍼지는 형태(flat response)가 됩니다.

    • 이는 국소화 손실 Llocalize (식 6)에서 목표로 하는 가우시안 형태(특정 위치에 집중된 형태)에서 벗어나게 되어 손실 값이 커집니다.

    • 따라서 최적화 과정에서 Llocalize를 최소화하려면 각 토큰이 서로 다른 이미지 위치에 명확하고 뾰족한 가우시안 형태의 어텐션 봉우리를 형성하도록 학습을 유도하게 됩니다. 이는 결과적으로 서로 다른 토큰들이 서로 다른 위치에 집중하고, 따라서 서로 유사한 어텐션 분포를 가지지 않도록 만듭니다.

• 부분집합을 이용한 최적화 안정화 (Stabilizing optimization by working with a subset)

  • 문제: 실험 결과, 일부 이미지에서는 특정 토큰의 어텐션 맵이 넓게 퍼지거나 불안정해지는 현상(예: 가려짐(occlusion) 등)이 발생하여 최적화 과정을 저해했습니다.

  • 해결책: 전체 토큰 중 가장 국소화가 잘 된 상위 $\kappa$개의 토큰에 대해서만 손실 함수를 적용하여 최적화를 진행합니다.

  • 작동 방식:

    • 각 토큰의 어텐션 맵($\tilde{M}_n$)이 얼마나 국소적인지는 목표 가우시안 분포($G_n$)와의 Kullback-Leibler (KL) 발산 값을 측정하여 판단합니다. KL 발산 값이 작을수록 분포가 비슷하다는 뜻이므로, 국소적인 가우시안 형태에 가까울수록 KL 발산 값은 작아집니다.

    • 이후 KL 발산 값에 음수를 취한 뒤, 이 값이 가장 큰 상위 $\kappa$개의 토큰 인덱스 집합 $N(\kappa)$를 반환합니다. 이는 곧 KL 발산 값이 가장 작은 (즉, 가장 국소화가 잘 된) 상위 $\kappa$개의 토큰을 선택하는 것과 같습니다.

    • 실제 최적화 과정에서는 이 $N(\kappa)$에 포함된 토큰들에 대해서만 손실 Llocalize와 Lequiv를 계산하고 적용하여 최적화의 안정성을 높입니다.

• 최종 키포인트 선정 (Final keypoints)

  • 문제: 최적화 과정에서 토큰들이 서로 다른 위치에 집중하도록 유도했지만, 이것만으로는 객체의 중요한 부위를 모두 커버하는 키포인트를 얻는다고 보장할 수 없습니다.

  • 해결책: 최적화 완료 후, 학습 이미지 전체에 대해 상위 $\kappa$개 토큰의 최대 반응 위치($\mu_i$)를 추출하고, 여기서 Furthest Point Sampling (FPS)을 사용하여 최종 키포인트 $K$개를 선정합니다.

  • 작동 방식:

    • 학습 데이터셋의 각 이미지에 대해 최적화된 토큰 중 상위 $\kappa$개에 해당하는 토큰들의 최대 반응 위치 집합 $\{\mu_i | i \in N(\kappa)\}$을 얻습니다.

    • 이 위치 집합에 FPS 알고리즘을 적용하여 원하는 개수 $K$만큼의 키포인트를 선택합니다. FPS는 주어진 점들 중에서 가장 멀리 떨어져 있는 점들을 순차적으로 선택하여 분포를 최대한 커버하는 장점이 있습니다.

    • 이렇게 각 이미지마다 $K$개의 키포인트 위치를 선택한 뒤, 학습 데이터셋 전체에서 가장 자주 등장한(선택된) 상위 $K$개의 토큰을 최종 키포인트로 선정합니다. 이는 데이터셋 전체에서 일관성 있게 나타나는 의미론적 위치에 해당하는 토큰을 선택하는 효과를 가집니다.

쿨백-라이블러 발산(Kullback-Leibler Divergence, KL Divergence)이란?

쿨백-라이블러 발산(KL Divergence)은 확률 분포 간의 차이를 측정하는 방법 중 하나입니다. 하나의 확률 분포가 다른 확률 분포와 얼마나 다른지를 정량화하는 데 사용됩니다.

• 목적: 두 확률 분포 P와 Q가 있을 때, P가 Q로부터 얼마나 '발산'하는지, 즉 얼마나 다른지를 측정합니다.

• 수학적 정의 (이산 확률 분포의 경우):

  $D_{KL}(P \parallel Q) = \sum_x P(x) \log\left(\frac{P(x)}{Q(x)}\right)$

  여기서 $P(x)$와 $Q(x)$는 변수 $x$에 대한 두 분포의 확률 값입니다. 로그 안의 비율이 1이면 (P(x) = Q(x)), 로그 값이 0이 되어 해당 $x$에 대한 기여분은 0이 됩니다. 비율이 클수록 (P(x)가 Q(x)에 비해 훨씬 클수록) 값은 커집니다.

• 성질:

  • KL 발산은 항상 0보다 크거나 같습니다 ($D_{KL}(P \parallel Q) \ge 0$).

  • 두 분포가 완전히 같을 때만 0입니다 ($D_{KL}(P \parallel Q) = 0 \iff P = Q$).

  • 대칭적이지 않습니다. 즉, $D_{KL}(P \parallel Q)$는 일반적으로 $D_{KL}(Q \parallel P)$와 다릅니다. 그래서 '거리'라고 부르기보다는 '발산' 또는 '차이'라고 부릅니다.

• 논문에서의 사용:

  • 논문에서는 각 토큰의 어텐션 맵($\tilde{M}_n$)을 정규화하여 확률 분포처럼 취급하고, 이를 목표하는 단일 모드 가우시안 분포($G_n$)와 비교합니다.

  • $G_n$은 특정 위치에만 집중된 이상적인 분포입니다.

  • $\tilde{M}_n$과 $G_n$ 간의 KL 발산 값이 작을수록, $\tilde{M}_n$은 $G_n$처럼 특정 위치에 잘 집중된 형태라고 볼 수 있습니다. 즉, KL 발산은 어텐션 맵의 국소화 정도를 측정하는 지표로 사용됩니다.

  • 쿨백 라이블러 발산의 음수를 취하여, 그 값이 클수록 국소화가 잘 된 것으로 판단하고, 이를 기준으로 상위 $\kappa$개 토큰을 선택합니다.

Furthest Point Sampling (FPS)을 사용하여 최종 키포인트 K개를 선정하는 알고리즘

이 논문에서 최종 키포인트를 선정하는 과정은 최적화된 토큰들 중 가장 '대표적인' K개를 고르는 과정입니다. FPS는 주어진 점들 중에서 가장 멀리 떨어져 있는 점들을 순차적으로 선택하는 알고리즘이며, 이는 점들의 분포를 가장 효과적으로 커버하는 부분집합을 찾을 때 유용합니다.

1. 최적화 완료 후 준비: 텍스트 임베딩 최적화가 완료되면, 각 학습 이미지에 대해 국소화가 잘 된 상위 $\kappa$개의 토큰을 선택합니다. 각 선택된 토큰($i \in N(\kappa)$)에 대해 해당 이미지에서의 최대 어텐션 반응 위치($\mu_i$)를 기록합니다.

2. 이미지별 FPS 적용: 각 학습 이미지마다, 해당 이미지에서 선택된 상위 $\kappa$개 토큰들의 최대 반응 위치 집합 $\{\mu_i | i \in N(\kappa)\}$가 있습니다. 이 $\kappa$개의 위치에서 FPS 알고리즘을 사용하여 K개의 위치를 선택합니다.

   • FPS 알고리즘 (K개 선택):

     • 첫 번째 점은 보통 주어진 점들 중 임의의 하나를 선택하거나, 이미 계산된 점들 중 가장 멀리 있는 점을 선택합니다. 논문에서는 어떻게 첫 점을 고르는지는 명시하지 않았으나, 일반적인 FPS 구현 방식입니다.

     • 나머지 K-1개의 점을 반복적으로 선택합니다. 각 단계에서는 이미 선택된 점들의 집합으로부터 가장 멀리 떨어져 있는 점을 현재 고려 중인 점들 중에서 선택합니다. '거리'는 보통 유클리드 거리를 사용합니다.

     • 이 과정을 K개의 점을 모두 선택할 때까지 반복합니다.

   • 이렇게 각 학습 이미지에 대해 K개의 최대 반응 위치가 선택됩니다. 더 중요한 것은 이 K개의 위치에 해당하는 원래 토큰의 인덱스입니다.

3. 데이터셋 전체 토큰 빈도 계산: 모든 학습 이미지에 대해 2단계를 수행합니다. 그러면 각 이미지에서 K개의 토큰 인덱스 집합이 나옵니다. 이 모든 이미지에서 선택된 토큰 인덱스들을 모아서, 원래 전체 N개의 토큰 중에서 각 토큰이 몇 번이나 이미지별 FPS 결과로 선택되었는지 빈도를 계산합니다.

4. 최종 키포인트 선정: 빈도 계산 결과, 학습 데이터셋 전체에서 가장 자주 선택된 상위 K개의 토큰을 최종적인 키포인트를 나타내는 토큰으로 결정합니다.

FPS를 사용하는 이유:

• 최적화 후 상위 $\kappa$개의 토큰은 모두 국소화가 잘 되었지만, 여전히 서로 매우 가깝거나 유사한 위치에 집중하는 토큰들이 있을 수 있습니다.

• FPS는 이러한 밀집된 영역에서 중복되는 토큰 대신, 객체 전반에 걸쳐 다양한 위치에 퍼져 있는 토큰들을 선택하는 데 도움을 줍니다.

• 학습 데이터셋 전체에 대해 FPS 결과를 종합하는 것은, 특정 이미지에 국한되지 않고 데이터셋의 다양한 예시에서 일관성 있게 중요한 위치에 대응하는 토큰을 최종 키포인트로 선택하게 하는 효과가 있습니다.

• 최종 키포인트 선택:

  • 최적화 과정을 통해 κ개의 토큰이 이미지 내에서 국소화된 어텐션 맵을 갖도록 학습됩니다.
  • 하지만 실제 필요한 키포인트의 수는 K개(K < κ)입니다.
  • 따라서 학습된 κ개의 국소화된 토큰 위치({μᵢ | i ∈ N(κ)})에서 각 학습 이미지에 대해 Furthest Point Sampling (FPS) 방식을 사용하여 K개의 키포인트를 선택합니다.
  • FPS는 주어진 점들 중에서 가장 멀리 떨어진 점들을 순차적으로 선택하는 알고리즘입니다. 이를 통해 이미지 전체에 걸쳐 키포인트가 고르게 분포되도록 합니다.
  • 수식 (10)은 이 과정을 나타냅니다:
    $K = \text{FPS}_K ( \{ \mu_i \mid i \in \mathcal{N}(\kappa) \} ) \quad (10)$
    • $K$: 최종 선택될 키포인트의 개수.
    • $\text{FPS}_K(\cdot)$: Furthest Point Sampling 함수로, 입력 집합에서 K개의 점을 선택합니다.
    • $\{\mu_i \mid i \in \mathcal{N}(\kappa)\}$: 최적화 과정을 통해 국소화된 것으로 확인된 κ개의 토큰에 해당하는 공간적 위치(어텐션 맵의 최대값 위치) 집합입니다.
  • 주의할 점은 FPS로 선택된 K개의 키포인트 집합이 이미지마다 다를 수 있다는 것입니다.
  • 따라서 최종적으로 데이터셋 전체에 일관적으로 사용될 K개의 키포인트는 모든 학습 이미지에서 FPS 결과로 가장 자주 나타난 K개의 토큰을 선택하여 결정합니다.

3.3 Implementation details

• 테스트 시 앙상블 (Test-time ensembling)

  • 새로운 이미지에 대해 키포인트를 예측할 때, 단순히 원본 이미지의 어텐션 맵을 사용하지 않습니다.

  • SuperPoint, Unsupervised Semantic Correspondence Using Stable Diffusion 등의 이전 연구들처럼, 테스트 이미지에 여러 가지 어파인 변환(affine transformations, 학습 시 등가성 손실에 사용된 것과 동일한 변환들)을 적용합니다.

  • 각 변환된 이미지에 대해 어텐션 맵을 계산합니다.

  • 계산된 어텐션 맵들을 다시 원래 이미지 공간으로 역변환(inverse-transform)합니다.

  • 이 역변환된 어텐션 맵들을 평균하여 최종 어텐션 맵으로 사용합니다. 이 과정을 통해 키포인트 예측의 안정성과 정확도를 높일 수 있습니다.

  • 수식 (11)은 이 과정을 나타냅니다:

    $\tilde{M} \leftarrow \frac{1}{I} \sum_i T_i^{-1} (M(e, T_i(X))) \quad (11)$

    • $\tilde{M}$: 테스트 시 앙상블을 통해 얻은 최종 어텐션 맵.

    • $I$: 사용된 변환(augmentation)의 개수.

    • $T_i$: i번째 어파인 변환.

    • $T_i^{-1}$: i번째 어파인 변환의 역변환.

    • $M(e, T_i(X))$: 변환된 이미지 $T_i(X)$에 대해 텍스트 임베딩 $e$로 계산된 어텐션 맵.

• 어텐션 맵 업샘플링 (Upsampling attention maps)

  • Stable Diffusion [44]과 같은 잠재 확산 모델에서 추출된 어텐션 맵은 일반적으로 해상도가 낮습니다 (예: 16x16 또는 32x32).

  • 정확한 키포인트 위치를 얻기 위해, 어텐션 맵을 계산하기 전에 U-Net의 해당 레이어에서 추출된 쿼리(Query) $Q$를 더 높은 해상도(예: 128x128)로 업샘플링합니다.

  • 논문에서는 간단하지만 효과적인 방법으로 바이큐빅 보간법(bicubic interpolation)을 사용하여 쿼리를 업샘플링했습니다.

4. Results

4.1 정량평가

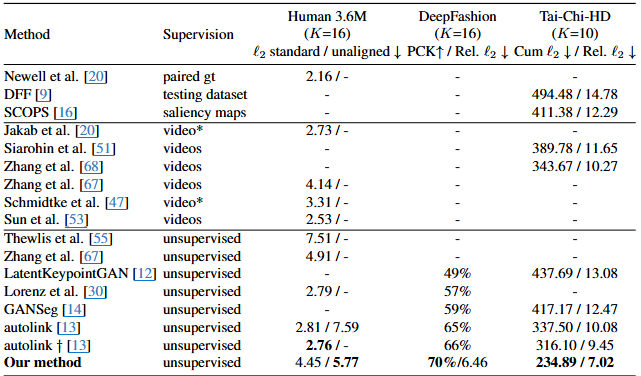
다양한 휴먼 포즈 데이터셋(Human 3.6M, DeepFashion, Tai-Chi-HD)에서 여러 키포인트 추정 방법들의 성능을 비교한 표입니다. 각 행은 다른 방법을 나타내고, 각 열은 사용된 데이터셋, 방법의 학습 방식(Supervision), 그리고 해당 데이터셋에 대한 평가 지표를 보여줍니다.

• Method (방법): 사용된 키포인트 추정 방법의 이름입니다. 논문에서 제안하는 방법은 'Our method'로 표시되어 있습니다.

• Supervision (학습 방식): 각 방법이 어떤 종류의 학습 데이터나 추가 정보를 사용하는지를 나타냅니다.

  • paired gt: 쌍으로 연결된 Ground Truth(실제 정답) 데이터를 사용한 지도 학습입니다.
  • testing dataset: 테스트 데이터를 사용합니다.
  • saliency maps: 눈에 띄는 영역을 나타내는 Saliency Map을 사용한 약한 지도 학습입니다.
  • videos: 비디오 데이터를 활용하여 학습합니다. * 표시는 추가적인 지도 정보(예: 쌍으로 연결되지 않은 GT, T-pose)를 사용했음을 나타냅니다.
  • unsupervised: 레이블이 지정되지 않은 데이터를 사용하여 학습하는 비지도 학습 방법입니다. 본 논문의 방법도 여기에 해당합니다.

• Human 3.6M (K=16): Human 3.6M 데이터셋에 대한 결과로, 16개의 키포인트를 사용했습니다.

  • ℓ₂ standard / unaligned ↓: ℓ₂ 오류(Euclidean distance)를 나타내며, 값이 낮을수록 성능이 좋습니다(↓ 표시). standard는 데이터가 잘 정렬(aligned)된 경우의 결과이고, unaligned는 데이터 정렬이 완화된 경우의 결과입니다. 본 논문의 방법은 4.45 / 5.77을 기록했습니다.

• DeepFashion (K=16): DeepFashion 데이터셋에 대한 결과로, 16개의 키포인트를 사용했습니다.

  • PCK↑ / Rel. ℓ₂ ↓: 두 가지 평가 지표를 사용합니다.
    • PCK↑: Percentage of Correct Keypoints(올바르게 추정된 키포인트 비율)로, 값이 높을수록 성능이 좋습니다(↑ 표시).
    • Rel. ℓ₂ ↓: 상대적인 ℓ₂ 오류로, 값이 낮을수록 성능이 좋습니다(↓ 표시).
  • 본 논문의 방법은 70% / 6.46을 기록했습니다.

• Tai-Chi-HD (K=10): Tai-Chi-HD 데이터셋에 대한 결과로, 10개의 키포인트를 사용했습니다.

  • Cum ℓ₂ ↓ / Rel. ℓ₂ ↓: 두 가지 평가 지표를 사용합니다.
    • Cum ℓ₂ ↓: 누적 ℓ₂ 오류로, 값이 낮을수록 성능이 좋습니다(↓ 표시).
    • Rel. ℓ₂ ↓: 상대적인 ℓ₂ 오류로, 값이 낮을수록 성능이 좋습니다(↓ 표시).
  • 본 논문의 방법은 234.89 / 7.02를 기록했습니다.

결과 분석:

• 표에서 볼 수 있듯이, 본 논문의 Our method는 비지도 학습(unsupervised) 방식입니다.

• Human 3.6M의 경우, 데이터가 잘 정렬된 standard 설정에서는 일부 지도 학습이나 비디오를 활용한 방법에 비해 성능이 약간 떨어지지만, unaligned 설정에서는 기존 비지도 방법들(Thewlis et al., Zhang et al.)보다 훨씬 우수한 성능을 보여줍니다.

• DeepFashion 데이터셋에서는 PCK에서 70%를 달성하며 기존의 비지도 방법들(LatentKeypointGAN, Lorenz et al., GANSeg, Autolink)보다 월등히 뛰어난 성능을 보여줍니다. PCK 70%는 다른 방법들의 최고 성능(Autolink †의 66%)을 넘어서는 결과입니다.

• Tai-Chi-HD 데이터셋은 인간 자세 데이터셋 중 가장 도전적인 데이터셋으로 설명되어 있습니다. 본 논문의 방법은 이 데이터셋에서 누적 ℓ₂ 오류 234.89와 상대 ℓ₂ 오류 7.02를 기록하며, 모든 비교 대상 방법들(심지어 지도 학습이나 비디오 기반 방법들 포함) 중에서 가장 우수한 성능을 보여줍니다.

• 'standard, unaligned 데이터의 차이

  • 데이터 정렬(Data Alignment)은 이미지 데이터셋을 특정 기준에 맞게 전처리하는 과정을 의미합니다. 특히 객체나 사람을 대상으로 하는 데이터셋에서 흔히 사용됩니다.
  • Aligned (잘 정렬된 경우):
    • 이미지 내에서 주요 객체(예: 얼굴, 전신)가 일관된 위치, 크기, 방향으로 나타나도록 이미지를 자르고(crop), 크기를 조절하고(resize), 경우에 따라서는 회전시키는 등 전처리가 적용된 경우입니다.
    • 예를 들어, 모든 사람 이미지가 정면을 보고 중앙에 위치하며 비슷한 크기로 보이도록 처리될 수 있습니다.
    • 이는 모델이 학습할 때 객체의 위치나 크기 변화에 덜 영향을 받도록 하여 학습을 용이하게 만드는 장점이 있습니다.
  • Unaligned (데이터 정렬이 완화된 경우):
    • Aligned 경우와 같은 엄격한 전처리가 적용되지 않거나, 전처리가 적용되더라도 객체의 위치나 크기, 방향에 더 큰 변화(variability)가 허용되는 경우입니다.
    • 논문에서 Human 3.6M의 unaligned 설정에 대해 "bounding box에서 사람까지의 여백을 100픽셀로 자르고, 중심 편향을 제거하기 위해 최대 100픽셀의 균일 랜덤 변환을 추가한다"고 설명하고 있습니다. 이는 standard(잘 정렬된) 설정보다 객체가 이미지 내에서 차지하는 위치나 크기가 훨씬 다양해짐을 의미합니다.
    • Unaligned 데이터는 실제 "in-the-wild" 환경(카메라 각도, 거리, 배경 등이 통제되지 않는 상황)을 더 잘 시뮬레이션합니다.
    • Unaligned 데이터셋에서 좋은 성능을 보이는 방법이 실제 응용 분야에서 더 실용적일 가능성이 높습니다. 본 논문의 방법이 unaligned 설정에서 기존 방법들보다 월등히 뛰어난 성능을 보인다는 것은 중요한 강점입니다.

• Percentage of Correct Keypoints(올바르게 추정된 키포인트 비율)

  • Percentage of Correct Keypoints (PCK)는 객체 검출이나 자세 추정에서 모델이 얼마나 정확하게 키포인트 위치를 예측했는지를 측정하는 일반적인 지표입니다.

  • 계산 방법:

    • 먼저 각 이미지와 각 키포인트에 대해 예측된 키포인트 위치와 Ground Truth(실제 정답) 키포인트 위치 사이의 유클리드 거리(L2 거리)를 계산합니다.

    • 사전 정의된 임계값(threshold)을 설정합니다. 이 임계값은 보통 이미지 크기나 객체 크기(예: 바운딩 박스 대각선 길이, 몸통 길이 등)의 일정 비율로 정하거나, 특정 픽셀 값으로 정합니다 (예: 논문의 DeepFashion 데이터셋에서는 6-pixel threshold를 사용).

    • 계산된 거리가 이 임계값보다 작거나 같으면, 해당 키포인트는 '올바르게 추정되었다(Correct)'고 판정합니다.

    • PCK는 테스트 데이터셋에 있는 모든 키포인트 중에서 '올바르게 추정된 키포인트의 총 개수'를 '전체 키포인트의 총 개수'로 나눈 후 100을 곱하여 백분율로 나타낸 값입니다.

    • PCK 값이 높을수록 모델의 키포인트 예측 정확도가 높다는 것을 의미합니다.

• 누적 ℓ₂ 오류와 상대적인 ℓ₂ 오류

  • 두 지표 모두 예측된 키포인트와 Ground Truth 키포인트 간의 거리 기반 오차를 측정합니다. ℓ₂ 오류는 유클리드 거리를 의미합니다. 예측된 키포인트 위치를 $(x_p, y_p)$, Ground Truth 위치를 $(x_{gt}, y_{gt})$라고 할 때, 개별 키포인트의 ℓ₂ 오류는 $\sqrt{(x_p - x_{gt})^2 + (y_p - y_{gt})^2}$ 입니다.

  • 누적 ℓ₂ 오류 (Cumulative ℓ₂ Error):

    • 주로 데이터셋 전체 또는 특정 그룹의 키포인트에 대한 ℓ₂ 오류를 모두 더한 값입니다.

    • 예를 들어, 테스트 데이터셋에 여러 이미지가 있고 각 이미지에 여러 개의 키포인트가 있다면, 각 이미지의 모든 키포인트에 대한 ℓ₂ 오류를 계산하고, 이를 테스트셋의 모든 이미지에 대해 합산하는 방식입니다.

    • 이 값 자체는 이미지나 객체의 크기에 영향을 많이 받습니다. 절대적인 오차의 합을 나타냅니다. 논문에서는 Tai-Chi-HD 데이터셋에서 사용되었고, 'Cum ℓ₂ ↓'로 표시되어 값이 낮을수록 좋음을 나타냅니다.

  • 상대적인 ℓ₂ 오류 (Relative ℓ₂ Error):

    • 개별 키포인트의 ℓ₂ 오류를 어떤 정규화 요소(normalization factor)로 나눈 값입니다. 이는 객체나 이미지의 크기 변화에 따른 오차의 영향을 줄여서, 다른 크기의 객체나 이미지 간의 성능 비교를 용이하게 합니다.

    • 정규화 요소의 예:

      • 이미지의 대각선 길이
      • 객체의 바운딩 박스 크기 (너비, 높이, 또는 대각선)
      • 객체 내의 특정 거리 (예: 얼굴 데이터셋의 눈 사이 거리)
      • 논문에서는 Human 3.6M 및 Tai-Chi-HD 데이터셋 비교를 위해 이미지 해상도를 128x128로 정규화한 후의 ℓ₂ 오류를 'Rel. ℓ₂'로 보고하며, 이는 128 픽셀 등의 고정 값으로 오차를 나눈 것일 수 있습니다. 이를 통해 여러 데이터셋에서 동일한 척도로 비교할 수 있습니다.

    • 상대 ℓ₂ 오류 값이 낮을수록 예측이 Ground Truth에 더 가깝다는 것을 의미하며, 크기에 관계없이 정확도가 높다는 것을 나타냅니다. 논문에서는 'Rel. ℓ₂ ↓'로 표시되어 값이 낮을수록 좋음을 나타냅니다.

4.2 정성평가

• 각 서브 피규어 설명:

  • (a) CelebA 데이터셋 키포인트: 인물 사진에서 얼굴의 주요 부위(눈, 코, 입 등)에 키포인트가 일관되게 표시됩니다.
  • (b) CUB-200-2011 데이터셋 키포인트: 새 이미지에서 부리, 눈, 날개, 다리 등 새의 특정 신체 부위에 키포인트가 표시됩니다.
  • (c) Tai-Chi-HD 데이터셋 키포인트: 태극권을 하는 사람들의 다양한 자세 이미지에서 팔, 다리, 몸통 등의 주요 관절 및 신체 부위에 키포인트가 표시됩니다.
  • (d) DeepFashion 데이터셋 키포인트: 패션 모델의 전신 이미지에서 주요 관절 및 신체 부위, 옷의 특정 지점 등에 키포인트가 표시됩니다.
  • (e) Human 3.6M 데이터셋 키포인트: 단순한 배경에서 특정 동작을 하는 사람의 이미지에 키포인트가 표시됩니다. 이 경우 마스크가 적용된 잘 정돈된(cropped and masked) 데이터를 사용했습니다.
  • (f) Unaligned Human 3.6M 데이터셋 키포인트: (e)와 동일한 Human 3.6M 데이터셋이지만, 본 논문에서 제안하는 완화된(relaxed) 정렬 방식을 적용한 이미지에 키포인트가 표시됩니다.

• 키포인트의 의미: 이미지 위에 표시된 다양한 색상의 점들과 숫자는 본 논문의 방법으로 학습된 '비지도 키포인트'입니다. 각 색상과 숫자는 특정 텍스트 임베딩(text embedding)에 의해 활성화되는 영역의 중심점을 나타내며, 이는 해당 영역이 데이터셋 내 이미지들에서 의미적으로 일관된 위치임을 시사합니다.

• 주요 시사점: 이 그림은 이미지의 외형 변화(자세, 의상, 배경 등)에도 불구하고 본 논문의 방법이 데이터셋 내에서 의미적으로 일관된 위치에 키포인트를 잘 찾아내는 것을 보여줍니다. 특히 Tai-Chi-HD와 같이 도전적인 데이터셋이나 정렬되지 않은(unaligned) Human 3.6M 데이터셋에서도 안정적인 키포인트를 추출하는 것은 제안된 방법의 강점을 잘 드러냅니다.