Abstract

• 문제 정의: 인간-컴퓨터 상호작용에 중요한 3D 손 자세 추정은 단일 RGB 이미지만으로는 어렵습니다. 이는 3D 자세 추정에 필요한 깊이 정보가 RGB 이미지에서 모호하기 때문입니다.
• 제안하는 해결책: 논문에서는 "2.5D 자세 표현(2.5D pose representation)"이라는 새로운 방법을 제안합니다. 이 표현은 단일 이미지에서 자세를 추정할 때 발생하는 깊이 및 스케일 모호성을 해결하는 데 도움이 됩니다.
• 2.5D 자세 표현의 특징: 이 표현은 자세를 스케일 인자(scaling factor)까지 추정합니다. 손 크기에 대한 사전 정보가 있다면 이 스케일 인자를 추가로 추정하여 실제 3D 자세를 얻을 수 있습니다.
• 사용된 기술: 새로운 CNN(Convolutional Neural Network) 아키텍처를 사용하여 깊이 맵(depth maps)과 히트맵 분포(heatmap distributions)를 암묵적으로(implicitly) 학습합니다.
• 연구 성과: 제안된 시스템은 심한 가려짐(severe occlusions)이 있는 등 여러 어려운 데이터셋에서 2D 및 3D 손 자세 추정 분야의 최신 기술(state-of-the-art) 수준의 성능을 달성했습니다.

1. Introduction

• 문제 정의: 단일 RGB 이미지에서 손의 3D 포즈(각 관절의 3D 좌표)를 추정하는 것은 어렵습니다.

  • RGB 이미지에는 깊이 정보가 부족하여 3D 공간에서의 손 크기(scale)와 카메라로부터의 거리(depth)를 정확히 알기 어렵습니다. 이를 scale 및 depth 모호성이라고 합니다.
  • 이러한 모호성 때문에 단순히 3D 포즈를 직접 추정하려 하면 잘 작동하지 않거나 특정 환경과 피험자에 과도하게 맞춰지는(over-fitting) 문제가 발생할 수 있습니다.

• 논문의 해결책: 이 논문은 문제를 두 개의 하위 문제로 분해하여 해결합니다.

  • 새로운 2.5D 포즈 표현 도입: 단일 RGB 이미지에서 모호성 없이 쉽게 추정할 수 있는 새로운 2.5D 포즈 표현을 사용합니다.
    • 이 2.5D 포즈는 손의 각 주요 지점(keypoint)의 이미지 상에서의 2D 좌표와, 손바닥(root)을 기준으로 정규화된 깊이 값으로 구성됩니다.
    • 깊이 값은 특정 손 뼈(bone)의 길이가 3D 공간에서 일정하도록 스케일 정규화(scale normalization)됩니다. 이를 통해 스케일이 정규화된 절대 3D 포즈를 직접 복원할 수 있습니다.
    • 이 2.5D 표현은 스케일 및 이동(translation)에 불변하며, RGB 이미지로부터 쉽게 추정 가능합니다.
  • 새로운 CNN 아키텍처 제안: 2.5D 포즈를 이미지로부터 추정하기 위한 새로운 CNN 아키텍처를 제안합니다.
    • 기존에는 2D 포즈 추정에 주로 사용되는 Heatmap Regression과 3D 포즈 추정에 사용되는 Holistic Pose Regression 방식이 있었습니다. Heatmap Regression은 2D 위치 정확도가 높지만 3D에서는 계산 비용이 크고, Holistic Regression은 3D에 적합하지만 2D 위치 정확도가 떨어지는 단점이 있었습니다.
    • 논문은 2.5D 포즈(2D 좌표와 깊이 값 모두 포함) 추정을 위해 2.5D Heatmaps라는 새로운 Heatmap 표현 방식을 제안합니다.
    • 이 2.5D Heatmaps는 2D 위치 추정을 위한 2D Heatmaps와 깊이 추정을 위한 Depth Map으로 구성됩니다.
    • 특히, 이 Heatmaps는 사람이 직접 설계하는 것이 아니라, CNN이 학습 과정에서 자동으로 최적의 형태로 잠재적(latent) 방식으로 학습하도록 설계되었습니다.
    • 학습된 2.5D Heatmaps는 미분 가능한 Softargmax 연산을 통해 2.5D 좌표로 변환됩니다. 이 과정은 네트워크의 end-to-end 학습을 가능하게 합니다.
    • 이렇게 얻어진 2.5D Heatmaps는 컴팩트하고 스케일 및 이동에 불변하며, sub-pixel 정확도로 키포인트 위치를 찾을 수 있는 잠재력을 가집니다.

• 결과: 제안된 방식은 심각한 가려짐(occlusions), 손과 객체의 상호작용, 실제 환경 이미지 등 다양한 어려운 데이터셋에서 2D 및 3D 손 포즈 추정에서 최첨단 성능을 달성했습니다.

2. Related Works

추후 작성.

3. Hand Pose Estimation

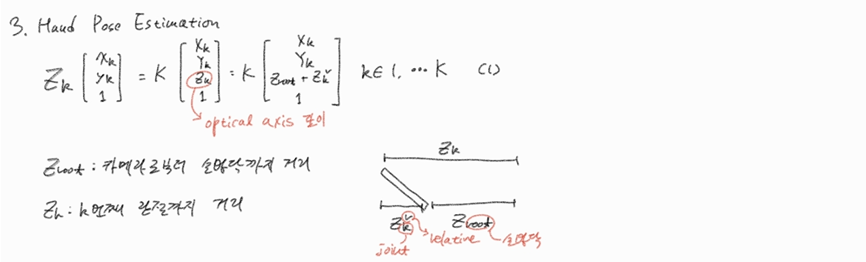
단일 RGB 이미지에서 3D 핸드 포즈를 추정하기 위해 제안된 접근 방식의 개요를 설명하며, 3D 공간의 특정 키포인트와 2D 이미지 상의 해당 키포인트 간의 관계를 나타내는 원근 투영 공식에 대해 설명합니다.

제시된 공식 (1)은 다음과 같습니다.

이 공식은 3D 공간의 핸드 키포인트 위치($P_k$)와 이미지 평면 상의 해당 2D 투영($p_k$) 사이의 관계를 보여줍니다. 각 항에 대해 자세히 살펴보겠습니다.

• $k$: 추정하고자 하는 핸드의 $K=21$개 키포인트 중 하나를 나타내는 인덱스입니다.

• $\begin{pmatrix} x_k \\ y_k \\ 1 \end{pmatrix}$: $p_k = (x_k, y_k) \in \mathbb{R}^2$는 이미지 $I$ 상에서 $k$번째 키포인트의 2D 픽셀 좌표를 나타냅니다. 여기에 1을 추가하여 동차 좌표(homogeneous coordinates) 형태로 표현한 것입니다.

• $Z_k$: $k$번째 키포인트의 카메라 좌표계 상에서의 깊이(depth) 값입니다. 즉, 카메라로부터 해당 키포인트까지의 거리를 나타내며 밀리미터(mm) 단위로 측정됩니다. 원근 투영에서 이 깊이 값은 3D 점이 2D 이미지에 투영될 때의 스케일을 결정하는 역할을 합니다.

• $\mathbf{K}$: 카메라의 내재 변수(intrinsic parameters) 행렬입니다. 이 행렬에는 카메라의 초점 거리(focal length)와 주점(principal point) 위치 등 카메라 자체의 기하학적 특성이 담겨 있습니다. 이미지 센서의 픽셀 크기 및 왜곡 계수 등도 포함될 수 있지만, 일반적으로는 단순화된 형태로 표현됩니다. 이 행렬은 3D 카메라 좌표계 상의 점을 2D 이미지 평면으로 변환하는 역할을 합니다.

• $\begin{pmatrix} X_k \\ Y_k \\ Z_k \\ 1 \end{pmatrix}$: $P_k = (X_k, Y_k, Z_k) \in \mathbb{R}^3$는 3D 카메라 좌표계 상에서 $k$번째 키포인트의 위치를 나타냅니다. 여기에 1을 추가하여 동차 좌표 형태로 표현한 것입니다. $Z_k$는 위에서 설명한 깊이 값과 동일합니다. Z-축은 카메라의 광축(optical axis)과 일치합니다.

• $\begin{pmatrix} X_k \\ Y_k \\ Z_{root} + Z^r_k \\ 1 \end{pmatrix}$: 이는 $k$번째 키포인트의 3D 위치 $P_k$를 다르게 표현한 것입니다.

  • $Z_{root}$: 루트 키포인트(이 논문에서는 손바닥)의 깊이 값입니다.
  • $Z^r_k = Z_k - Z_{root}$: $k$번째 키포인트의 깊이 $Z_k$에서 루트 키포인트의 깊이 $Z_{root}$를 뺀 값으로, 루트 키포인트에 대한 상대적인 깊이(root-relative depth)를 나타냅니다. 이 논문에서는 2.5D 포즈 표현에 이 상대 깊이 값($Z^r_k$)을 사용합니다.

이 공식은 3D 점을 2D 이미지로 투영하는 표준적인 방식입니다. 하지만 단일 RGB 이미지에서 3D 포즈를 추정하는 것은 역방향 문제(ill-posed problem)이며, 특히 깊이($Z_k$)와 스케일(scale)에 대한 모호성이 크게 작용합니다. 공식에서 볼 수 있듯이, 3D 점의 깊이($Z_k$)는 2D 투영 좌표($x_k, y_k$)의 스케일을 결정하며, 단일 2D 이미지로는 이 $Z_k$ 값을 정확히 알아내기 어렵습니다.

이 논문에서는 이러한 어려움을 해결하기 위해 $Z_k$ 대신 루트 키포인트에 대한 상대적인 깊이($Z^r_k$)를 사용하는 새로운 2.5D 포즈 표현 방식을 제안하고, 이를 통해 단일 이미지에서 스케일 및 이동 변환에 불변(scale and translation invariant)인 포즈 정보를 효과적으로 추정할 수 있도록 합니다.

3.1 2.5D Pose Representation

단일 RGB 이미지에서 바로 절대적인 3D 포즈를 추정하는 것은 스케일이나 깊이에 대한 모호성 때문에 어렵기 때문에, 논문에서는 이 2.5D 포즈를 중간 단계로 사용합니다.주 요 내용은 다음과 같습니다.

• 정의: 2.5D 포즈 $P^{2.5D}_k$는 각 키포인트 k에 대해 다음과 같이 정의됩니다.

  $P^{2.5D}_k = (x_k, y_k, Z^r_k)$
  • $k \in K$: 손의 모든 키포인트 집합을 나타냅니다 (이 논문에서는 21개).
  • $(x_k, y_k) \in \mathbb{R}^2$: 입력 이미지에서 k번째 키포인트의 2D 픽셀 좌표입니다.
  • $Z^r_k = Z_k - Z_{root}$: k번째 키포인트의 깊이($Z_k$)에서 루트 키포인트(Z_{root})의 깊이를 뺀 값, 즉 루트 키포인트에 대한 상대적인 깊이입니다. 이 논문에서는 손바닥(palm)을 루트 키포인트로 사용합니다.

• 스케일 정규화: 위 2.5D 포즈는 여전히 절대적인 스케일 정보를 포함하고 있지 않기 때문에, 스케일 정규화 과정을 거칩니다. 이는 특정 두 키포인트(예: 검지 손가락의 첫 번째 관절(MCP)과 손바닥) 사이의 3D 공간 거리가 항상 일정한 값 C가 되도록 전체 3D 포즈의 스케일을 조정하는 것입니다. 이렇게 정규화된 3D 포즈 $\hat{P}$는 다음과 같습니다.

  $\hat{P} = \frac{C}{s} \cdot P$
  • $P$: 원래의 3D 포즈입니다.
  • $s = \|P_n - P_{parent(n)}\|_2$: 정규화에 사용되는 두 키포인트(n, parent(n)) 사이의 원래 3D 거리입니다.
  • $C$: 정규화 후 두 키포인트 사이의 고정된 거리 값입니다 (논문에서는 C=1 사용).

  이 스케일 정규화 결과, 2.5D 포즈는 다음과 같이 정규화된 2.5D 표현 $\hat{P}^{2.5D}_k$가 됩니다.

  $\hat{P}^{2.5D}_k = (x_k, y_k, \hat{Z}r_k)$
  • $(x_k, y_k)$: 2D 좌표는 스케일 정규화에 의해 변하지 않습니다.
  • $\hat{Z}^r_k$: 스케일 정규화된 루트에 대한 상대적인 깊이입니다.

• 사용 이유 및 장점:

  • 단일 RGB 이미지에서 절대적인 3D 포즈를 직접 추정하기 어려운 문제를 해결합니다.
  • 2.5D 포즈는 이미지에서 모호성 없이 쉽게 복원될 수 있습니다.
  • 스케일 및 이동(translation)에 불변(invariant)합니다.
  • 밀집된 픽셀 단위 예측이 가능합니다.
  • 다양한 소스의 학습 데이터를 활용할 수 있는 멀티태스크 학습에 용이합니다.
  • 스케일 인자까지 포함하는 절대적인 3D 포즈를 정확하게 복원할 수 있는 기반을 제공합니다.

이 논문에서는 이러한 2.5D 포즈 표현을 사용함으로써 단일 RGB 이미지로부터 손의 2D 위치와 루트에 대한 상대적인 깊이를 효과적으로 추정하고, 이를 기반으로 3D 손 포즈를 복원하는 방법을 제안합니다.

3.2 3D Pose Reconstruction from 2.5D

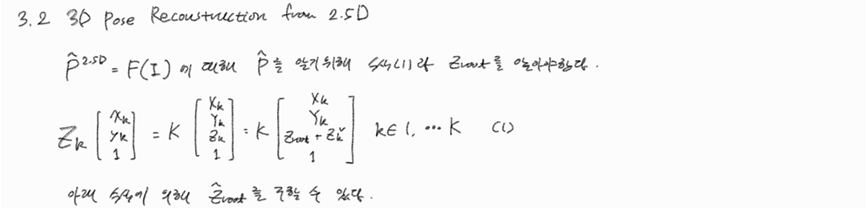
3.2절에서는 제안된 2.5D 포즈 표현으로부터 3D 포즈를 복원하는 방법에 대해 설명합니다. 주요 내용은 다음과 같습니다.

• 목표: RGB 이미지($I$)로부터 예측된 2.5D 포즈($\hat{P}^{2.5D} = F(I)$)와 카메라 고유 파라미터($K$)를 이용하여 손의 3D 포즈($\hat{P}$)를 복원하는 것입니다.

• 문제점: 단일 RGB 이미지에서 3D 포즈를 추정하는 것은 깊이 정보의 모호성(scale and depth ambiguities) 때문에 어려운 문제입니다.

• 해결 방법: 본 논문에서는 2.5D 포즈와 카메라 파라미터가 주어졌을 때, 특정 두 키포인트 간의 3D 공간 거리가 일정하다는 제약(constraint)을 사용하여 모호성을 해결하고 루트 키포인트(손바닥)의 깊이($\hat{Z}_{root}$)를 계산합니다.

• 제약 조건: 스케일 정규화된 3D 포즈 $\hat{P}$에서 두 키포인트 $n$과 $m$ (논문에서는 검지손가락의 첫 번째 관절(MCP)과 손바닥(root) 키포인트 사용) 사이의 유클리드 거리가 상수 $C$가 된다는 제약을 사용합니다.

  • 제약 조건 수식:
    $(\hat{X}_n - \hat{X}_m)^2 + (\hat{Y}_n - \hat{Y}_m)^2 + (\hat{Z}_n - \hat{Z}_m)^2 = C^2\quad (3)$
    • $\hat{X}_k, \hat{Y}_k, \hat{Z}_k$: 스케일 정규화된 3D 카메라 좌표계 상의 $k$번째 키포인트 좌표.
    • $C$: 정규화 시 사용되는 상수 거리 (논문에서는 $C=1$ 사용).

• 루트 깊이($\hat{Z}_{root}$) 계산:

  • 카메라 투영 모델 (식 1)과 키포인트의 깊이 $\hat{Z}_k = \hat{Z}_{root} + \hat{Zr}_k$ ( $\hat{Zr}_k$: 루트 대비 상대 깊이) 관계를 이용하여 식 (3)을 2D 좌표 $(x_k, y_k)$와 $\hat{Z}_{root}$, $\hat{Zr}_k$에 대한 식으로 변환합니다.

  • 이 과정에서 식 (5)와 같이 $\hat{Z}_{root}$에 대한 2차 방정식이 도출됩니다.

    $(x_n(\hat{Z}_{root} + \hat{Zr}_n) - x_m(\hat{Z}_{root} + \hat{Zr}_m))^2 + (y_n(\hat{Z}_{root} + \hat{Zr}_n) - y_m(\hat{Z}_{root} + \hat{Zr}_m))^2+ ((\hat{Z}_{root} + \hat{Zr}_n) - (\hat{Z}_{root} + \hat{Zr}_m))^2 = C^2$

    • $x_k, y_k$: 이미지 픽셀 좌표 상의 $k$번째 키포인트 좌표.
    • $\hat{Zr}_k$: 스케일 정규화된 $k$번째 키포인트의 루트 대비 상대 깊이.
    • $\hat{Z}_{root}$: 루트 키포인트의 깊이 (구하려는 값).
    • $n, m$: 정규화에 사용되는 두 키포인트.
    • $C$: 상수 거리.

  • 이 2차 방정식을 정리하면 $a\hat{Z}_{root}^2 + b\hat{Z}_{root} + c = 0$ 형태가 되며, 계수 $a, b, c$는 식 (6)과 같습니다.

    • $a = (x_n - x_m)^2 + (y_n - y_m)^2$
    • $b = \hat{Zr}_n(x_n^2 + y_n^2 - x_n x_m - y_n y_m) + \hat{Zr}_m(x_m^2 + y_m^2 - x_n x_m - y_n y_m)$
    • $c = (x_n \hat{Zr}_n - x_m \hat{Zr}_m)^2 + (y_n \hat{Zr}_n - y_m \hat{Zr}_m)^2 + (\hat{Zr}_n - \hat{Zr}_m)^2 - C^2$

  • 이 2차 방정식의 해를 근의 공식으로 구하면 $\hat{Z}_{root}$ 값이 두 개 나옵니다.

    • $\hat{Z}_{root} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

  • 논문에서는 이 두 해 중 카메라 전면에 해당하는 해를 선택합니다 (식 7 참고).

• 최종 3D 포즈 복원: 계산된 $\hat{Z}_{root}$와 2.5D 포즈 $\hat{P}^{2.5D}$ (2D 좌표 $(x_k, y_k)$와 상대 깊이 $\hat{Zr}_k$), 그리고 카메라 파라미터 $K$를 사용하여 식 (1)에 따라 각 키포인트의 3D 좌표를 역투영하여 스케일 정규화된 3D 포즈 $\hat{P}$를 복원합니다.

• 스케일 복원: 복원된 스케일 정규화된 3D 포즈로부터 실제 절대 스케일 $s$는 추가적인 단계 (식 8)를 통해 추정할 수 있다고 언급합니다.

결론적으로, 이 섹션은 2.5D 포즈 표현의 핵심 이점 중 하나인 '스케일 및 깊이 모호성 제거'를 활용하여, 제약 조건을 만족하는 유일한 루트 깊이를 계산함으로써 3D 포즈를 기하학적으로 복원하는 방법을 제시합니다.

3.3 Scale Recovery

• 문제 정의: 2.5D 포즈 추정은 손의 3D 포즈를 스케일 인자(scaling factor)에 비례하여 추정합니다. 즉, 포즈의 '형태'는 알 수 있지만 실제 손의 크기는 알 수 없습니다. 따라서 절대적인 3D 포즈를 얻기 위해서는 이 스케일 인자를 별도로 추정해야 합니다.

• 스케일 추정 방법: 논문에서는 손의 절대 스케일($s$)을 알 수 없는 경우, 학습 데이터에서 얻은 손 뼈 길이의 평균($\mu_{kl}$)을 활용하여 스케일($\hat{s}$)을 추정합니다. 이는 추정된 스케일 정규화 3D 포즈($\hat{P}_k$, $\hat{P}_l$)에서 계산된 뼈 길이와 학습 데이터의 평균 뼈 길이 간의 차이를 최소화하는 스케일($s$)을 찾는 최적화 문제로 정의됩니다. 수식 (8)은 다음과 같습니다.

  $\hat{s} = \text{argmin}_s \sum_{k,l \in E} (s \cdot \| \hat{P}_k - \hat{P}_l \| - \mu_{kl})^2 \quad (8)$

  • $\hat{s}$: 추정하려는 절대 스케일 인자입니다.

  • $\text{argmin}_s$: 수식 우변의 값을 최소화하는 $s$ 값을 찾으라는 의미입니다.

  • $\sum_{k,l \in E}$: 손의 운동학적 구조(kinematic structure)를 정의하는 뼈대($E$)에 속하는 모든 키포인트 쌍($k$와 $l$)에 대해 합산하라는 의미입니다.

  • $s \cdot \| \hat{P}_k - \hat{P}_l \|$: 추정된 스케일 정규화 3D 포즈($\hat{P}_k, \hat{P}_l$)에 스케일 $s$를 곱하여 얻은 절대적인 3D 공간에서의 키포인트 $k$와 $l$ 사이의 거리입니다.

  • $\mu_{kl}$: 학습 데이터에서 얻은 키포인트 $k$와 $l$ 사이의 뼈 길이 평균입니다.

  • $(s \cdot \| \hat{P}_k - \hat{P}_l \| - \mu_{kl})^2$: 스케일 $s$를 적용한 추정 뼈 길이와 학습 데이터 평균 뼈 길이 간의 차이의 제곱입니다. 이 값을 모든 뼈대에 대해 합산하여 최소화함으로써 가장 적절한 스케일 $\hat{s}$를 찾습니다.

• 필요성: 이 스케일 복구 과정은 손 크기에 대한 사전 정보가 없을 때 특히 중요합니다. 2.5D 포즈 자체는 스케일과 독립적이지만, 현실 세계의 절대적인 3D 위치를 알기 위해서는 손의 실제 크기를 알아야 하기 때문입니다.

• 2.5D 정규화와의 관계: 논문 앞부분(3.1절)에서는 인덱스 손가락의 첫 번째 관절(MCP)과 손바닥(root) 사이의 거리를 $C=1$로 정규화하여 스케일 정규화된 2.5D 포즈 $\hat{P}^{2.5D}$를 얻는다고 언급합니다. 3.2절에서 이 $\hat{P}^{2.5D}$와 카메라 내부 매개변수를 이용해 스케일 정규화된 3D 포즈 $\hat{P}$를 복원한 뒤, 이 $\hat{P}$를 기반으로 3.3절의 스케일 복구 과정을 통해 실제 3D 포즈 $P$를 얻게 됩니다. 이 방법은 손 크기에 대한 사전 정보 없이도 단일 RGB 이미지에서 3D 손 포즈를 효과적으로 추정할 수 있게 해줍니다.

4. 2.5D Pose Regression

• 전체 손실 함수 ($\mathcal{L}$): 2.5D 포즈 $\hat{P}^{2.5D}$를 예측하기 위한 전체 손실 함수는 다음과 같이 두 부분으로 구성됩니다.

  $\mathcal{L}(\hat{P}^{2.5D}) = \mathcal{L}_{xy} (p, p^{gt}) + \alpha\mathcal{L}_{\hat{Z}^r} (\hat{Z}^r , \hat{Z}^{r,gt})$
  • 여기서 $\hat{P}^{2.5D}$는 예측된 2.5D 포즈를, $p$는 예측된 2D 포즈를, $\hat{Z}^r$는 예측된 각 키포인트의 루트(손바닥) 기준 상대 깊이 값을 의미합니다. $p^{gt}$와 $\hat{Z}^{r,gt}$는 각각 해당 값들의 정답(ground-truth)입니다.

• 2D 포즈 손실 함수 ($\mathcal{L}_{xy}$):

  • 이 부분은 손의 2D 키포인트 위치($p$)를 정확하게 예측하는 데 사용됩니다.
  • $\mathcal{L}_{xy} (p, p^{gt})$는 예측된 2D 포즈 $p$와 정답 2D 포즈 $p^{gt}$ 간의 차이에 대한 손실을 계산합니다.

• 루트 기준 상대 깊이 손실 함수 ($\mathcal{L}_{\hat{Z}^r}$):

  • 이 부분은 각 손 키포인트의 루트 기준 상대 깊이 값($\hat{Z}^r$)을 정확하게 예측하는 데 사용됩니다.
  • $\mathcal{L}_{\hat{Z}^r} (\hat{Z}^r , \hat{Z}^{r,gt})$는 예측된 루트 기준 상대 깊이 $\hat{Z}^r$와 정답 $\hat{Z}^{r,gt}$ 간의 차이에 대한 손실을 계산합니다. $\hat{Z}^r = \{ \hat{Z}^r_k \}_{k \in K}$는 전체 키포인트 $K$에 대한 루트 기준 상대 깊이 값들의 집합입니다.

• 가중치 ($\alpha$):

  • $\alpha$는 2D 포즈 손실($\mathcal{L}_{xy}$)과 루트 기준 상대 깊이 손실($\mathcal{L}_{\hat{Z}^r}$) 간의 균형을 맞추는 가중치 역할을 합니다. 논문에서는 실험적으로 $\alpha=20$을 사용했다고 언급합니다.

• 손실 함수의 장점:

  • 이 손실 함수는 다양한 종류의 학습 데이터를 활용할 수 있게 합니다.
  • 예를 들어, 2D 포즈만 주석(annotation)된 'in-the-wild' 이미지와 정확한 3D 포즈 주석이 있는 제한된 환경 또는 합성 이미지를 모두 사용할 수 있습니다.
  • $\mathcal{L}_{xy}$는 모든 학습 샘플에 대해 유효하지만, $\mathcal{L}_{\hat{Z}^r}$는 3D 포즈 주석이 제공될 때만 손실 계산에 포함됩니다.

연구 진행 연결:
이 손실 함수 구성은 2D 정보와 3D 정보를 동시에 학습하는 방식의 초기 연구 방향을 보여줍니다. 이후 연구들, 예를 들어 📄 InterHand2.6M: A Dataset and Baseline for 3D Interacting Hand Pose Estimation from a Single RGB Image와 같은 데이터셋 기반 연구들은 이러한 멀티태스크 학습 방식을 더욱 복잡한 환경(예: 두 손 상호작용)으로 확장하며, 손실 함수의 형태나 학습 방식에 대한 추가적인 탐구를 진행했습니다. 이는 단일 손의 2.5D 포즈 추정을 넘어 현실 세계의 복잡한 손 동작을 모델링하는 데 중요한 진전을 가져왔습니다.

4.1. Direct 2.5D Heatmap Regression

이 섹션에서는 논문에서 제안하는 새로운 2.5D 히트맵 표현 방식 중 하나인 'Direct 2.5D Heatmap Regression'에 대해 설명합니다.

• 배경: 전통적으로 2D 포즈 추정에서는 히트맵 회귀(Heatmap regression) [24, 25, 55, 56] 방식이 많이 사용됩니다. 이는 관절의 위치를 직접 좌표로 회귀하는 대신, 이미지 각 픽셀에서 특정 관절이 존재할 확률을 나타내는 2D 히트맵을 예측하는 방식입니다. 이 방식은 출력이 이미지 해상도와 같아 관절 위치를 더 정확하게 찾을 수 있다는 장점이 있습니다. 하지만 3D 포즈 추정에서 3D 공간의 볼륨 형태 히트맵 [28]을 사용하면 계산량과 메모리 비용이 매우 커지는 문제가 있습니다.

• 2.5D 히트맵 제안: 이러한 문제를 해결하기 위해 논문에서는 '2.5D 히트맵'이라는 새롭고 컴팩트한 표현 방식을 제안합니다. 2.5D 히트맵은 다음과 같이 두 가지 요소로 구성됩니다.

  • 2D 히트맵 ($H^{2D}$): 이미지 상에서 각 관절의 위치를 나타내는 2D 확률 분포입니다.
  • Depth 맵 ($H^{\hat{z}r}$): 각 픽셀에 대해 Root(손바닥) 관절을 기준으로 정규화된 상대적인 깊이 값을 나타냅니다.

• 2.5D 히트맵의 특징: 이 방식의 Depth 맵은 절대적인 깊이나 스케일에 불변하며, 유사한 손 포즈에 대해 일관성을 유지하므로 CNN으로 학습하기가 더 용이합니다.

• 네트워크 출력: CNN은 총 2K개의 채널을 출력합니다. 여기서 K는 손 관절의 개수(본 논문에서는 21개)이며, K개 채널은 2D 히트맵 ($H^{2D}$)을, 나머지 K개 채널은 Depth 맵 ($H^{\hat{z}r}$)을 나타냅니다.

• 타겟 히트맵 정의 (학습 시): 학습을 위해 Ground truth (정답) 히트맵이 필요하며, 이는 다음과 같이 정의됩니다.

  • 2D 타겟 히트맵 ($H^{2D,gt}_k$): k번째 관절의 2D 타겟 히트맵은 다음과 같이 정의됩니다.
    $H^{2D,gt}_k (p) = \exp\left(-\frac{\lVert p - p^{gt}_k \rVert}{\sigma^2}\right), \quad p \in \Omega \quad (10)$
    • $H^{2D,gt}_k (p)$: k번째 관절에 대한 픽셀 위치 $p$에서의 Ground truth 2D 히트맵 값입니다.
    • $p$: 이미지 내의 임의의 픽셀 위치입니다.
    • $p^{gt}_k$: k번째 관절의 Ground truth 2D 위치 좌표입니다.
    • $\lVert p - p^{gt}_k \rVert$: 픽셀 $p$와 Ground truth 위치 $p^{gt}_k$ 사이의 유클리드 거리입니다.
    • $\sigma$: 가우시안 분포의 표준 편차를 제어하는 값입니다. 히트맵의 '퍼짐' 정도를 결정합니다. 본 논문에서는 $\sigma=5$를 사용합니다.
    • $\Omega$: 이미지 I의 모든 픽셀 위치 집합입니다.
    • 이 식은 $p^{gt}_k$를 중심으로 하는 가우시안 분포 형태를 갖는 2D 히트맵을 정의합니다.
  • Depth 타겟 맵 ($H^{\hat{z}r}_k$): Ground truth Depth 맵은 직접적으로 정의하기 어렵기 때문에, 논문에서는 Ground truth 2D 히트맵과 Ground truth 정규화된 상대 깊이 값을 곱하여 정의합니다.
    $H^{\hat{z}r}_k = \hat{Z}^{r,gt}_k \cdot H^{2D,gt}_k \quad (11)$
    • $H^{\hat{z}r}_k$: k번째 관절에 대한 Depth 타겟 맵입니다.
    • $\hat{Z}^{r,gt}_k$: k번째 관절의 Ground truth 정규화된 Root 기준 상대 깊이 값입니다.
    • $H^{2D,gt}_k$: k번째 관절의 Ground truth 2D 히트맵입니다.
    • 이 식은 2D 히트맵이 높은 위치($p^{gt}_k$ 근처)에서 Ground truth 상대 깊이 값을 갖는 Depth 맵을 생성합니다.

• 추론 시 관절 위치 및 깊이 값 얻기: 학습된 CNN으로부터 얻은 히트맵을 사용하여 추론 시 각 관절의 위치와 깊이 값을 얻습니다.

  • 2D 관절 위치 ($p_k$): k번째 관절의 2D 위치는 2D 히트맵 $H^{2D}_k$에서 값이 가장 높은 픽셀 위치로 결정됩니다.

    $p_k = \underset{p}{\operatorname{argmax}} H^{2D}_k(p) \quad (12)$
    • $p_k$: k번째 관절의 추정된 2D 위치입니다.
    • $\underset{p}{\operatorname{argmax}}$: 주어진 표현식 $H^{2D}_k(p)$의 값을 최대로 만드는 픽셀 위치 $p$를 찾는 연산입니다.
    • $H^{2D}_k(p)$: k번째 관절에 대해 네트워크가 예측한 2D 히트맵 값입니다.

  • Depth 값 ($\hat{Z}^r_k$): k번째 관절의 깊이 값은 Depth 맵 $H^{\hat{z}r}_k$에서 위에서 찾은 2D 관절 위치 $p_k$에 해당하는 값으로 결정됩니다.

    $\hat{Z}^r_k = H^{\hat{z}r}_k (p_k) \quad (13)$
    • $\hat{Z}^r_k$: k번째 관절의 추정된 정규화된 Root 기준 상대 깊이 값입니다.
    • $H^{\hat{z}r}_k (p_k)$: k번째 관절에 대해 네트워크가 예측한 Depth 맵에서 2D 추정 위치 $p_k$에 해당하는 값입니다.

• Direct 방식의 한계: 이 방식은 2D 포즈 추정 성능을 크게 향상시키지만, 타겟 히트맵이 수동으로 설계된다는 점([σ가 모든 관절에 고정] 등)과 Depth 맵의 정의가 직관적이지 않을 수 있다는 한계가 있습니다. 이러한 한계는 다음 섹션인 Latent 2.5D Heatmap Regression에서 다루어집니다.

이 섹션에서 설명된 Direct 2.5D Heatmap Regression은 2D 히트맵의 정확한 위치 추정 능력과 2.5D 표현의 컴팩트함을 결합하여 3D 포즈 추정 문제를 해결하려는 초기 시도입니다.

4.2. Latent 2.5D Heatmap Regression

• 기존 Heatmap Regression의 문제점:

  • 이전 섹션에서 2D Heatmap을 생성할 때 사용한 Gaussian 분포의 표준 편차($\sigma$)는 모든 키포인트에 대해 고정되어 학습되지 않았습니다. 이상적으로는 손가락 끝처럼 정밀한 위치가 중요한 부분은 Heatmap이 뾰족하게, 손바닥처럼 넓은 영역은 Heatmap이 완만하게 나와야 더 좋습니다 (Figure 2 참고).
  • Gaussian 분포는 2D 위치 추정에는 자연스럽지만, 깊이(Depth) 예측에는 직관적이지 않습니다. 손바닥처럼 깊이가 거의 일정한 부분에도 Gaussian 형태로 모델링되는 것은 비효율적입니다.
  • 수식 (12)의 argmax 연산은 미분 불가능하여 표준 편차와 같은 파라미터를 학습할 수 없습니다.

• Latent 2.5D Heatmap Representation 제안:

  • 이러한 문제점을 해결하기 위해, CNN의 출력(2K 채널)을 바로 Heatmap으로 사용하지 않고 "잠재 변수(latent variables)"인 $H^{*}_{2D_k}$ (2D heatmaps)와 $H^{*}_{\hat{z}_r k}$ (depth maps)로 간주합니다.
  • 네트워크는 미분 가능한 손실 함수를 최소화하는 방식으로 이 잠재적인 표현을 스스로 학습합니다.

• 잠재 Heatmap으로부터 2.5D 좌표 추출:

  • 2D 위치($p_k$) 추정: 각 키포인트 $k$의 잠재 2D Heatmap $H^{*}_{2D_k}$에 Spatial Softmax 정규화를 적용하여 확률 맵 $H_{2D_k}$를 만듭니다.

    • 수식 (14):
      $H_{2D_k}(p) = \frac{\exp(\beta_kH^{*}_{2D_k}(p))}{\sum_{p' \in \Omega} \exp(\beta_kH^{*}_{2D_k}(p'))}$
      • $H_{2D_k}(p)$: 픽셀 위치 $p$에서의 키포인트 $k$의 확률 값.
      • $H^{*}_{2D_k}(p)$: CNN이 출력한 키포인트 $k$의 잠재 2D Heatmap 값.
      • $\Omega$: Heatmap 상의 모든 픽셀 위치 집합.
      • $\beta_k$: 키포인트 $k$의 Heatmap 확산(spread)을 조절하는 학습 가능한 파라미터.
      • 이 수식은 각 키포인트의 Heatmap 값을 확률 분포로 변환합니다.
    • 수식 (15):
      $p_k = \sum_{p \in \Omega} H_{2D_k}(p) \cdot p$
      • $p_k$: 키포인트 $k$의 최종 2D 위치.
      • $H_{2D_k}(p)$: 위 Spatial Softmax로 얻은 확률 맵 값.
      • $p$: 현재 픽셀의 2D 좌표 벡터.
      • $\Omega$: 확률 맵 상의 모든 픽셀 위치 집합.
      • 이 수식은 확률 맵 상의 모든 픽셀 위치와 해당 확률 값을 곱하여 합산하는 방식으로, 확률 분포의 기댓값(Expected Value)을 계산합니다. 이는 soft-argmax 연산으로 알려져 있으며, 미분 가능하여 역전파 학습이 가능합니다.

  • 정규화된 상대 깊이($\hat{Z}_{r_k}$) 추정: 2D 위치를 얻은 후, 해당 깊이 값은 확률 맵 $H_{2D_k}$와 잠재 깊이 맵 $H^{*}_{\hat{z}_r k}$의 요소별 곱(Hadamard product, $\circ$)의 총합으로 계산됩니다.

    • 수식 (16):
      $\hat{Z}_{r_k} = \sum_{p \in \Omega} H_{2D_k}(p) \circ H^{*}_{\hat{z}_r k}(p)$
      • $\hat{Z}_{r_k}$: 키포인트 $k$의 최종 정규화된 루트(root) 기준 상대 깊이 값.
      • $H_{2D_k}(p)$: 위 Spatial Softmax로 얻은 확률 맵 값.
      • $H^{*}_{\hat{z}_r k}(p)$: CNN이 출력한 키포인트 $k$의 잠재 깊이 맵 값.
      • $\Omega$: 확률 맵 및 잠재 깊이 맵 상의 모든 픽셀 위치 집합.
      • 이 수식은 2D 위치 확률이 높은 영역에서 해당 잠재 깊이 맵 값을 가중 평균하는 효과를 가집니다. 이 연산 또한 미분 가능합니다.

• Latent Heatmap Regression의 장점:

  • Soft-argmax 및 관련 연산이 모두 미분 가능하여 네트워크 전체를 End-to-end 방식으로 학습할 수 있습니다.
  • 키포인트별로 Heatmap의 확산 정도를 조절하는 파라미터($\beta_k$)를 학습할 수 있습니다.
  • 깊이 맵 표현 방식을 수동으로 설계하지 않고도 암시적으로 학습할 수 있습니다.
  • 이러한 방식으로 학습된 Heatmap은 Figure 2에서 볼 수 있듯이 직접 Heatmap Regression (Convolutional pose machines, Stacked hourglass networks for human pose estimation)으로 얻은 Heatmap보다 더 적응적인 형태를 보입니다.