SELFEXPLAIN: A Self-Explaining Architecture for Neural Text Classifier

상솜공방·2025년 6월 3일

논문 리뷰

목록 보기

8/49

1. Introduction

interpretability for neural text classification

post-hoc explanation model:

사전 훈련된 모델의 결과를 가지고 설명

inherent interpretable model:

모델 내부에 설명 가능한 모듈이 내장돼있음
attention score를 기반으로 word-level feature attribution 을 사용하는 방식이 일반적
그러나 이는 신뢰성이 떨어진다는 것이 증명 됨

저자의 모델

글로벌, 로컬 해석 가능 레이어를 신경망 분류기에 삽입
word-level feature attribution 대신 구문 수준의 상위 이해

LIL

활성화 차이를 활용, 모델의 최종 분류에 대한 확률 분포와 토픽에 대한 연관성을 수량화 하여 보여줌

GIL

maximum inner product search를 활용, 입력 샘플과 가장 관련있는 토픽을 훈련 데이터에서 검색

2. SELFEXPLAIN

2.1 Defining human-interpretable concepts

수식

구(phrases)로 구성된 concept의 개념을 도입(아래 그림의 fantastic actor, fabulous acting 등)
$x = \{w_i\}_{1:T}$ : 시퀀스의 구성요소
$N(x) = \{nt_j\}_{1:J}$ : $x$ 를 비말단 구성요소로 분리한 것 ( $J$ 는 $x$ 의 비말단 요소의 개수)
$M$ : 분류 모델
- global explanation: $x_{train}$ 에서 생성된 $Q$ (concept store) 중 가장 영향력이 큰 $C_G$ 를 검색
- local explanation: $x$ 가 분리된 후 이들 각각의 영향력에 따라 $C_L$ 을 산출

예시

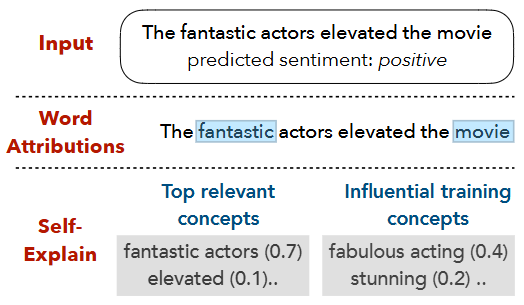
이 그림은 감성 분석 예제에서 SELFEXPLAIN 모델이 생성한 해석을 보여줍니다.
입력 문장은 "The fantastic actors elevated the movie"이며, 모델의 예측은 긍정(positive)입니다.
Word Attributions:
- 기존의 단어 수준 중요도(예: saliency map)에서 "fantastic", "movie"라는 단어들이 강조됨.
SELFEXPLAIN:
- Top relevant concepts (입력 내 핵심 구): "fantastic actors (0.7)", "elevated (0.1)" 등 구 단위 높은 가중치 부여.
- Influential training concepts (훈련 데이터 상 영향력 큰 개념): "fabulous acting (0.4)", "stunning (0.2)" 같은 훈련 데이터의 일관성 있는 긍정적 구 표현도 제공.

즉, SELFEXPLAIN은 단어 수준에서 끝나는 것이 아니라 구 문장 단위(phrases)를 개념으로 활용
입력 문장 내 중요한 구 뿐 아니라 훈련 데이터에서 유사한 개념들을 함께 보여 줌
모델 예측의 지역적(local) 및 전역적(global) 해석을 동시에 제공합니다.

2.2 Concept-Aware Encoder E

Concept에 대한 벡터 $u_j$ 계산

$x = \{w_i\}_{1:T}$ : 시퀀스의 구성요소
$\{h_i\}_{1:T}$ : $x$ 를 사전학습된 트랜스포머에 임베딩한 벡터
$N(x) = \{nt_j\}_{1:J}$ : $x$ 를 비말단 구성요소로 분리한 것 ( $J$ 는 $x$ 의 비말단 요소의 개수)
$\{u_j\}_{1:J}$ : concept의 임베딩 벡터로, 아래 수식에 의해 계산. 즉, 해당 구 내 모든 단어 임베딩을 벡터별로 더한 뒤, 단어 수로 나누어서 평균을 냄.

$u_j = \frac{\sum_{w_i \in nt_j} h_i}{\text{len}(nt_j)}$
- $w_i \in nt_j$ : $nt_j$ 에 포함된 단어들. 즉, $nt_j$ 가 "the good soup"라는 구라면, 이 안의 단어들은 "the", "good", "soup"입니다.
- $h_i$ : 입력 문장 내 단어 $w_i$ 의 transformer 최종 레이어의 임베딩 벡터.
- $\text{len}(nt_j)$ : 해당 구 $nt_j$ 에 포함된 단어의 개수. 예시에서 "the good soup"라면 3이 됨.
- $\sum_{w_i \in nt_j} h_i$ : 해당 구 내 모든 단어 임베딩 벡터의 합

예시

입력 문장: "The chef cooks the good soup"
구 $nt_j =$ "the good soup"
단어 임베딩 벡터 (크기 3이라고 가정):
- $h_{\text{the}} = [0.1, 0.1, 0.1]$
- $h_{\text{good}} = [0.2, 0.4, 0.1]$
- $h_{\text{soup}} = [0.6, 0.1, 0.1]$
단어 수: $\text{len}(nt_j) = 2$
벡터 합:
$h_{\text{the}} + h_{\text{good}} + h_{\text{soup}} = [0.9, 0.6, 0.3]$
평균:
$u_j = \frac{[0.9, 0.6, 0.3]}{3} = [0.3, 0.2, 0.1]$
"the good soup"이라는 구는 벡터 $u_j = [0.3, 0.2, 0.1]$ 로 표현되며, 이것이 모델 내에서 해당 구를 대표하는 개념 벡터로 쓰임.

루트 노드에 대한 벡터 $u_S$ 계산

$S$ : 신택스 트리의 루트 노드
$nt_S$ : 루트 노드에 대한 벡터. [CLS] 토큰의 출력 벡터 $u_s$ 로 나타냄 (이밖에 모든 벡터에 대한 mean pooling이나 sum pooling 등의 방법을 사용했을 때, 결과가 비슷했기에 [CLS] 토큰의 벡터를 사용)
$l_Y$ : $u_s$ 에 대한 분류 확률 분포.

$l_Y = \text{softmax}(W_y \times g(u_S) + b_y)$
- $g()$ : ReLU 함수
- $W_y$ : 가중치 행렬
- $b_y$ : 편향
$P_C = argmax(l_Y)$ : 예측된 클래스 인덱스

2.3 Local Interpretability Layer (LIL)

개념

SELFEXPLAIN은 NLP용 self-explaining 모델로서, 모델의 예측을 설명할 때 단어 단위가 아니라 구 구간(phrase) 단위의 개념(concepts)을 사용
LIL은 이러한 개념 각각이 최종 예측에 얼마나 기여하는지 local relevance score를 부여하여 정량화
이 기여도 계산은 컴퓨터 비전 분야에서 널리 쓰이는 활성화 차이(activation difference) 기법을 참고
활성화 차이란, 특정 입력 개념이 모델의 최종 출력에 미치는 영향을 그 개념을 포함했을 때와 제외했을 때 활성화값의 차이로 측정하는 것

수식

t_j = g(u_j) - g(u_S)

$u_j$ : 개념 $nt_j$ 의 임베딩 벡터
$u_S$ : [CLS] 토큰의 임베딩 벡터
$g$ : ReLU 활성화 함수
즉, 개념 $nt_j$ 의 표현 활성화에서 문장 전체 표현 활성화를 빼 준 값

s_j = \text{softmax}(W_v \times t_j + b_v)

$s_j$ : 개념 $nt_j$ 가 제외됐을 때 예측 레이블 분포
$W_v, b_v$ : 가중치와 편향 파라미터

r_j = (l_Y)_{i=PC} - (s_j)_{i=PC}

$l_Y$ : 전체 입력을 사용할 때 예측 클래스 PC에 대한 레이블 점수
$s_j$ : 구문 개념 $nt_j$ 를 제거했을 때의 예측 점수
$r_j$ : 최종적으로 각 구문 개념의 중요성 점수
두 점수 차가 클수록 해당 개념이 예측에 크게 기여했다는 뜻
결과적으로 중요도가 가장 높은 개념들 $C_L$ 이 모델 예측을 '로컬(local)'하게 설명

즉, LIL은 입력 문장을 구성하는 주요 문법 단위인 구(phrases) 하나하나가 모델의 최종 예측에 얼마나 영향을 미쳤는지를 활성화 차이를 통해 계산해, 해석 가능한 설명을 제공합니다.

코드 구현

def lil(self, hidden_state, nt_idx_matrix):
    # hidden_state: 문장 내 각 토큰의 임베딩 벡터.
    # nt_idx_matrix: 문장 내 각 구문이 어떤 토큰으로 이루어져있는지에 대한 정보를 인덱스화 한 것.

    phrase_level_hidden = torch.bmm(nt_idx_matrix, hidden_state)
    # 전체 구문에 원한 인코딩 된 구문별 인덱스를 곱하여 해당 구문이 아닌 것을 0으로 만듦.
    # hidden_state: [batch, seq_len, hidden_dim]
    # nt_idx_matrix: [batch, num_phrases, seq_len]
    # 결과: [batch, num_phrases, hidden_dim] (김, 철수) 는 각 벡터를 더해서 (김철수) 하나의 벡터로 생성됨.

    phrase_level_activations = self.activation(phrase_level_hidden)
    # 각 구문별 임베딩에 ReLU 활성화 함수를 적용

    pooled_seq_rep = self.sequence_summary(hidden_state).unsqueeze(1)
    # hidden_state: [batch_size, seq_len, hidden_dim]
    # self.sequence_summary(): 맨 앞의 [CLS] 토큰만 풀링 ([batch_size, hidden_dim])
    # unsqueeze(1): [batch_size, 1, hidden_dim]로 변환 (브로드 캐스팅을 위해)
    # 이렇게 하면 phrase_level_activations의 차원인 [batch, num_phrases, hidden_dim]과 알아서 차연산이 가능해짐
    
    phrase_level_activations = phrase_level_activations - pooled_seq_rep
    # 문장 전체 벡터를 통해 생성한 확률 - 위에서 계산한 확률
    
    phrase_level_logits = self.phrase_logits(phrase_level_activations)
    # 이 값을 nn.Linear() 분류기를 통과.
    # 논문의 수식과 달리 Softmax는 여기서 생략하고, 나중에 손실 함수에서 사용.
    
    return phrase_level_logits

코드와 수식 비교

1) 구문 임베딩 계산

phrase_level_hidden = torch.bmm(nt_idx_matrix, hidden_state)

역할:
- 각 구문(phrase)이 어떤 토큰들로 이루어져 있는지(=nt_idx_matrix)와
  각 토큰의 임베딩(hidden_state)을 곱해서
  구문별 임베딩 벡터( $u_j$ )를 만듭니다.
수식 매핑:
- $u_j$ (구문 임베딩 벡터)

torch.bmm() 연산의 예시

한 문장(batch=1), 5단어(seq_len=5), 3구문(num_phrases=3), 임베딩 차원 4

`hidden_state` (1, 5, 4)

[
  [
    [0.1, 0.2, 0.3, 0.4],  # 1번째 토큰
    [0.5, 0.6, 0.7, 0.8],  # 2번째 토큰
    [0.9, 1.0, 1.1, 1.2],  # 3번째 토큰
    [1.3, 1.4, 1.5, 1.6],  # 4번째 토큰
    [1.7, 1.8, 1.9, 2.0],  # 5번째 토큰
  ]
]

`nt_idx_matrix` (1, 3, 5)

[
  [
    [1, 0, 0, 0, 0],  # 1번째 구문: 1번째 토큰만 포함
    [0, 1, 1, 0, 0],  # 2번째 구문: 2,3번째 토큰 포함
    [0, 0, 0, 1, 1],  # 3번째 구문: 4,5번째 토큰 포함
  ]
]

연산 과정

1번째 구문 임베딩:

[1, 0, 0, 0, 0] × hidden_state
→ 1번째 토큰의 임베딩만 남음
→ [0.1, 0.2, 0.3, 0.4]

2번째 구문 임베딩:

[0, 1, 1, 0, 0] × hidden_state
→ 2,3번째 토큰의 임베딩을 더함
→ [0.5+0.9, 0.6+1.0, 0.7+1.1, 0.8+1.2]
→ [1.4, 1.6, 1.8, 2.0]

3번째 구문 임베딩:

[0, 0, 0, 1, 1] × hidden_state
→ 4,5번째 토큰의 임베딩을 더함
→ [1.3+1.7, 1.4+1.8, 1.5+1.9, 1.6+2.0]
→ [3.0, 3.2, 3.4, 3.6]

결과

phrase_level_hidden (1, 3, 4)

[
  [
    [0.1, 0.2, 0.3, 0.4],   # 1번째 구문
    [1.4, 1.6, 1.8, 2.0],   # 2번째 구문
    [3.0, 3.2, 3.4, 3.6],   # 3번째 구문
  ]
]

2) ReLU 활성화 적용

phrase_level_activations = self.activation(phrase_level_hidden)

역할:
- 구문 임베딩에 ReLU 활성화 함수( $g$ )를 적용
수식 매핑:
- $g(u_j)$

3) 문장 전체 임베딩(요약) 계산

pooled_seq_rep = self.sequence_summary(hidden_state).unsqueeze(1)

역할:
- 문장 전체를 대표하는 벡터( $u_s$ )를 뽑고,
  차원을 맞추기 위해 unsqueeze(1)로 shape을 맞춤
수식 매핑:
- $u_s$ (문장 전체 임베딩 벡터)

4) 활성화 차이 계산

phrase_level_activations = phrase_level_activations - pooled_seq_rep

역할:
- 각 구문별 활성화에서 문장 전체 활성화를 뺌
수식 매핑:
- $t_j = g(u_j) - g(u_s)$

5) 구문별 분류(로짓) 계산

phrase_level_logits = self.phrase_logits(phrase_level_activations)

역할:
- 구문별 활성화 차이( $t_j$ )를 선형 레이어(TimeDistributed Linear)에 통과시켜
  각 구문별 예측 로짓( $s_j$ )을 계산
수식 매핑:
- $s_j = \text{softmax}(W_v \times t_j + b_v)$
  (여기서 softmax는 보통 loss 계산 시 적용)

2.4 Global Interpretability layer (GIL)

개념

SELFEXPLAIN 모델의 Global Interpretability Layer(GIL)은 주어진 입력 샘플에 대해 훈련 데이터 내에서 가장 영향력 있는 개념 K개를 찾아 설명합니다. 이를 통해 새로운 입력에 대한 모델의 결정에 훈련 데이터의 어떤 개념들이 중요한 역할을 했는지 글로벌한 관점에서 이해할 수 있습니다.

개념 저장소 Q

q_k = \frac{\sum_{w \in q_k} e(w)}{len(q_k)} \in \mathbb{R}^D

Q = \{ q_1, q_2, ..., q_{N_Q} \}

$Q$ : 훈련 데이터에서 추출한 모든 개념들의 집합
$q_k$
- 수식을 살펴보면, $u_j$ 를 구하는 것과 동일합니다.
- 훈련 데이터에서 추출한 개념(phrase) 중 $k$ 번째 개념을 나타냅니다.
- SELFEXPLAIN 모델에서 개념 저장소 Q에 들어가는 개념 단위 중 하나입니다.
- 이 수식에서는 $q_k$ 의 벡터 표현을 정의하는 대상입니다.
$w \in q_k$
- $q_k$ 개념을 구성하는 단어 $w$ 를 의미합니다.
- 즉, $q_k$ 가 하나의 구(phrase)라면, 그 구에 속한 모든 단어들의 집합을 나타냅니다.
- 예: $q_k$ 가 "good movie"라는 구라면, $w$ 는 "good"과 "movie" 두 단어를 가리킵니다.
$e(w)$
- 모델 $M$ 에서 임베딩 레이어를 통해 얻은 단어 $w$ 의 임베딩 벡터입니다.
- 보통 $e(w) \in \mathbb{R}^D$ 형태로, $D$ 차원의 실수 벡터를 의미합니다.
- 단어 의미를 고차원 벡터 공간에 표현한 것으로, 문맥 임베딩(예: BERT, XLNet 등)일 수 있습니다.
$\sum_{w \in q_k} e(w)$
- $q_k$ 구에 속한 모든 단어들의 임베딩 벡터를 각각 더한 것, 즉 벡터들의 요소별 합입니다.
- 각 단어 임베딩 벡터를 차례로 더해서 하나의 벡터를 만듭니다.
$\text{len}(q_k)$
- $q_k$ 구에 포함된 단어의 개수(길이)를 나타냅니다.
- 예를 들어, 구 "good movie" 의 경우 두 단어이므로 $\text{len}(q_k) = 2$ 입니다.
$\frac{\sum_{w \in q_k} e(w)}{\text{len}(q_k)}$
- $q_k$ 구에 속한 모든 단어 임베딩 벡터의 평균을 계산하는 부분입니다.
- 단어 임베딩 벡터들의 합을 단어 수로 나누어 구 벡터를 만듭니다.
$\in \mathbb{R}^D$
- 계산된 $q_k$ 의 벡터 표현이 $D$ 차원의 실수 벡터 공간에 속한다는 의미입니다.
모델이 학습을 진행하면서 임베딩 레이어 $e(\cdot)$ 가 계속 업데이트되어 단어 및 개념 벡터 표현도 변합니다.
따라서, 훈련 데이터에서 추출된 각 개념의 임베딩 $q_k$ 도 시간이 지나면서 달라집니다.
이 때문에 인덱싱된 저장소 Q의 벡터들을 일정 주기(예: 매 몇 백 혹은 몇 천 학습 스텝마다)마다 다시 계산하고, 이를 인덱싱하여 최신 상태로 유지합니다.
이렇게 하면 GIL 레이어가 항상 최신 임베딩을 고려한 영향력 있는 개념들을 정확하게 검색할 수 있습니다.

입력 샘플에 대한 영향력 있는 개념 선택

d(x, q) = \frac{x \cdot q}{\|x\|\|q\|}, \quad \forall q \in Q

입력 샘플 $x$ 의 루트 노드 임베딩 $u_S$ 를 사용
이 표현이 개념 저장소의 각 개념 벡터와 코사인 유사도 계산
최대 내적 탐색(Maximum Inner Product Search, MIPS) 알고리즘을 사용해 효율적으로 상위 K개 검색

p(q | x_i) = \frac{\exp d(u_S, q)}{\sum_{q'} \exp d(u_S, q')}

선택된 각 개념에 대해 소프트맥스 확률 계산
이 접근법은 차별화 가능(differentiable)하여 역전파(back-propagation) 기반의 엔드투엔드 학습이 가능

코드 구현

## GIL 레이어 ##
# 문장 전체 벡터와 훈련 데이터의 개념 벡터들 사이의 내적을 통해 상위 K개의 개념을 추출
# 이 개념들에 대한 분류 결과 로짓 값과 그들의 인덱스를 계산
def gil(self, pooled_input): # pooled_input = sentence_cls: 문장 전체를 대표하는 벡터
    batch_size = pooled_input.size(0) # [batch_size, hidden_dim]의 size(0) = batch_size
    inner_products = torch.mm(pooled_input, self.concept_store.T)
    # self.concept_store = [num_concepts, hidden_dim]
    # 문장 전체 벡터와 개념 벡터들 사이의 내적을 계산
    # inner_products = [batch_size, num_concepts]

    _, topk_indices = torch.topk(inner_products, k=self.topk)
    # 유사도가 가장 높은 K개의 개념 인덱스 선택
    topk_concepts = torch.index_select(self.concept_store, 0, topk_indices.view(-1))
    # self.concept_store: [num_concepts, hidden_dim] (훈련 데이터에서 추출한 모든 개념(phrase) 벡터의 집합)
    # topk_indices: [batch_size, topk] 각 배치(문장)마다 유사도가 가장 높은 K개 개념의 인덱스
    # topk_indices.view(-1): [batch_size * topk]로 펼쳐서, 전체 배치의 K개 인덱스를 1차원으로 만듦
    # torch.index_select(self.concept_store, 0, ...) concept_store에서 해당 인덱스에 해당하는 개념 벡터만 추출
    # 결과 shape: [batch_size * topk, hidden_dim] 배치 내 모든 문장에 대해, 각 문장별로 topk 개념 벡터를 한 번에 뽑아냄

    topk_concepts = topk_concepts.view(batch_size, self.topk, -1).contiguous()
    # 위에서 뽑은 [batch_size * topk, hidden_dim] 텐서를 [batch_size, topk, hidden_dim]로 다시 reshape
    # .contiguous()는 메모리 상에서 연속적인 배열로 만들어줌(reshape 후 연산 최적화)
    # 각 배치(문장)마다 topk개의 개념 벡터를 3차원 텐서로 정렬
    # topk_concepts: [batch_size, topk, hidden_dim]

    concat_pooled_concepts = torch.cat([pooled_input.unsqueeze(1), topk_concepts], dim=1)
    # 문장 전체 벡터와 상위 K개 개념 벡터를 결합
    # concat_pooled_concepts: [batch_size, 1 + topk, hidden_dim]

    attended_concepts, _ = self.multihead_attention(query=concat_pooled_concepts,
                                                    key=concat_pooled_concepts,
                                                    value=concat_pooled_concepts)
    # 어텐션 멀티헤드 레이어를 통해 각 개념 벡터에 대한 가중치를 계산
    # 이 가중치는 문장 전체 벡터와 개념 벡터 사이의 유사도를 나타냄
    # 이 가중치를 통해 개념 벡터들을 조합하여 새로운 벡터를 생성
    # attended_concepts: [batch_size, 1 + topk, hidden_dim]

    gil_topk_logits = self.topk_gil_mlp(attended_concepts[:,0,:])
    # [batch_size, 1 + topk, hidden_dim]에서 [:, 0, :]는 각 배치의 0번째 벡터(즉, 문장 전체 벡터, 어텐션을 거친 후의 값)만 추출
    # 결과 shape: [batch_size, hidden_dim]
    # 이 벡터를 기준으로 [batch_size, hidden_dim] ->  [batch_size, num_classes]로 변환되는 nn.Linear() 클래시피케이션 레이어 통과

    # print(gil_topk_logits.size())
    # gil_logits = torch.mean(gil_topk_logits, dim=1)
    return gil_topk_logits, topk_indices

1) 입력 문장 임베딩

pooled_input:
- [batch_size, hidden_dim]
- 입력 샘플의 문장 전체 임베딩(보통 [CLS] 벡터, 수식의 $x$ 또는 $u_s$ )

2) 개념 저장소

self.concept_store:
- [num_concepts, hidden_dim]
- 훈련 데이터에서 추출한 모든 개념(구문) 벡터의 집합, 수식의 $Q$

3) 유사도(내적) 계산

inner_products = torch.mm(pooled_input, self.concept_store.T)

역할:
- 입력 문장 임베딩과 모든 개념 벡터의 내적(유사도) 계산
- 수식의 $x \cdot q$ (코사인 유사도와 거의 동일, 정규화만 없음)
shape:
- [batch_size, num_concepts]

4) 상위 K개 개념 선택

_, topk_indices = torch.topk(inner_products, k=self.topk)

역할:
- 유사도가 가장 높은 K개 개념의 인덱스를 선택
- 수식의 "상위 K개 선택"과 동일

5) 상위 K개 개념 벡터 추출

topk_concepts = torch.index_select(self.concept_store, 0, topk_indices.view(-1))
topk_concepts = topk_concepts.view(batch_size, self.topk, -1).contiguous()

역할:
- 선택된 K개 개념 벡터를 실제로 추출
- [batch_size, topk, hidden_dim]

topk_concepts = torch.index_select(self.concept_store, 0, topk_indices.view(-1))

설명:
- self.concept_store: [num_concepts, hidden_dim]
  - 훈련 데이터에서 추출한 모든 개념(phrase) 벡터의 집합
- topk_indices: [batch_size, topk]
  - 각 배치(문장)마다 유사도가 가장 높은 K개 개념의 인덱스
- topk_indices.view(-1):
  - [batch_size * topk]로 펼쳐서,
    전체 배치의 K개 인덱스를 1차원으로 만듦
- torch.index_select(self.concept_store, 0, ...)
  - concept_store에서 해당 인덱스에 해당하는 개념 벡터만 추출
  - 결과 shape: [batch_size * topk, hidden_dim]
즉:
- 배치 내 모든 문장에 대해, 각 문장별로 topk 개념 벡터를 한 번에 뽑아냄

topk_concepts = topk_concepts.view(batch_size, self.topk, -1).contiguous()

설명:
- 위에서 뽑은 [batch_size * topk, hidden_dim] 텐서를
  [batch_size, topk, hidden_dim]로 다시 reshape
- .contiguous()는 메모리 상에서 연속적인 배열로 만들어줌(reshape 후 연산 최적화)
즉:
- 각 배치(문장)마다 topk개의 개념 벡터를 3차원 텐서로 정렬

예시

batch_size = 2, topk = 3, hidden_dim = 4

topk_indices 예시:

[[5, 2, 7],   # 1번째 문장: 5,2,7번째 개념
 [1, 0, 3]]   # 2번째 문장: 1,0,3번째 개념

topk_indices.view(-1) → [5,2,7,1,0,3]
torch.index_select(...) →
- 6개 개념 벡터 추출: [6, 4]
.view(2, 3, 4) →
- [2, 3, 4]
  - 1번째 문장: 5,2,7번째 개념
  - 2번째 문장: 1,0,3번째 개념

정리

첫 줄:
- 배치 내 모든 문장에 대해, 각 문장별로 topk 개념 벡터를 한 번에 추출
둘째 줄:
- [batch_size, topk, hidden_dim] 형태로 배치별로 정렬

6) 입력 벡터와 개념 벡터 결합 및 멀티헤드 어텐션

concat_pooled_concepts = torch.cat([pooled_input.unsqueeze(1), topk_concepts], dim=1)

attended_concepts, _ = self.multihead_attention(
    query=concat_pooled_concepts,
    key=concat_pooled_concepts,
    value=concat_pooled_concepts

역할:
- 입력 문장 벡터와 상위 K개 개념 벡터를 하나로 합침
- [batch_size, topk+1, hidden_dim]
- 입력 벡터와 개념 벡터 간의 상호작용(관계)을 학습
- 어텐션을 통해 더 정교한 해석 가능

예시 값

batch_size = 2, topk = 3, hidden_dim = 4

pooled_input:

[
  [0.1, 0.2, 0.3, 0.4],  # 문장1
  [0.5, 0.6, 0.7, 0.8],  # 문장2
]  # shape: [2, 4]

topk_concepts:

[
  [  # 문장1
    [1.1, 1.2, 1.3, 1.4],  # 1번째 개념
    [2.1, 2.2, 2.3, 2.4],  # 2번째 개념
    [3.1, 3.2, 3.3, 3.4],  # 3번째 개념
  ],
  [  # 문장2
    [4.1, 4.2, 4.3, 4.4],
    [5.1, 5.2, 5.3, 5.4],
    [6.1, 6.2, 6.3, 6.4],
  ]
]  # shape: [2, 3, 4]

unsqueeze(1)로 차원 맞추기

pooled_input.unsqueeze(1)
- [2, 4] → [2, 1, 4]
- 각 문장별로 1개의 벡터(문장 전체 벡터)를 "구문"처럼 취급

cat으로 합치기

torch.cat([pooled_input.unsqueeze(1), topk_concepts], dim=1)
- [2, 1, 4]와 [2, 3, 4]를 dim=1(구문 차원)으로 합침
- 결과: [2, 4, 4]
  - 각 문장마다
    - [문장 전체 벡터, 1번째 개념, 2번째 개념, 3번째 개념]
    - 즉, 총 4개의 벡터(1+topk)로 구성

예시 결과

concat_pooled_concepts:

[
  [  # 문장1
    [0.1, 0.2, 0.3, 0.4],  # 문장 전체 벡터
    [1.1, 1.2, 1.3, 1.4],  # 1번째 개념
    [2.1, 2.2, 2.3, 2.4],  # 2번째 개념
    [3.1, 3.2, 3.3, 3.4],  # 3번째 개념
  ],
  [  # 문장2
    [0.5, 0.6, 0.7, 0.8],  # 문장 전체 벡터
    [4.1, 4.2, 4.3, 4.4],
    [5.1, 5.2, 5.3, 5.4],
    [6.1, 6.2, 6.3, 6.4],
  ]
]  # shape: [2, 4, 4]

attended_concepts, _ = self.multihead_attention(
    query=concat_pooled_concepts,
    key=concat_pooled_concepts,
    value=concat_pooled_concepts
)

멀티헤드 어텐션 적용

입력:
- query, key, value 모두 concat_pooled_concepts
- 즉, 문장 전체 벡터와 topk 개념 벡터들 간의 상호작용(관계)을 학습
동작:
- 각 문장에 대해
  - "문장 전체 벡터"가 topk 개념 벡터들과 어떻게 상호작용하는지
  - 어텐션을 통해 가중합/정보 교환
출력:
- attended_concepts: [batch_size, topk+1, hidden_dim]
  - 어텐션을 거친 후의 벡터들
  - 첫 번째(0번째) 벡터는 "문장 전체 벡터"에 해당

7) 최종 분류 레이어

gil_topk_logits = self.topk_gil_mlp(attended_concepts[:,0,:])

역할:
- 어텐션 결과(입력 벡터에 해당하는 부분)를 분류 레이어에 통과시켜
  최종적으로 예측에 반영할 로짓을 만듦

8) 반환값

return gil_topk_logits, topk_indices

역할:
- 최종 로짓과, 선택된 상위 K개 개념의 인덱스를 반환

2.5 Training

모델 아키텍처

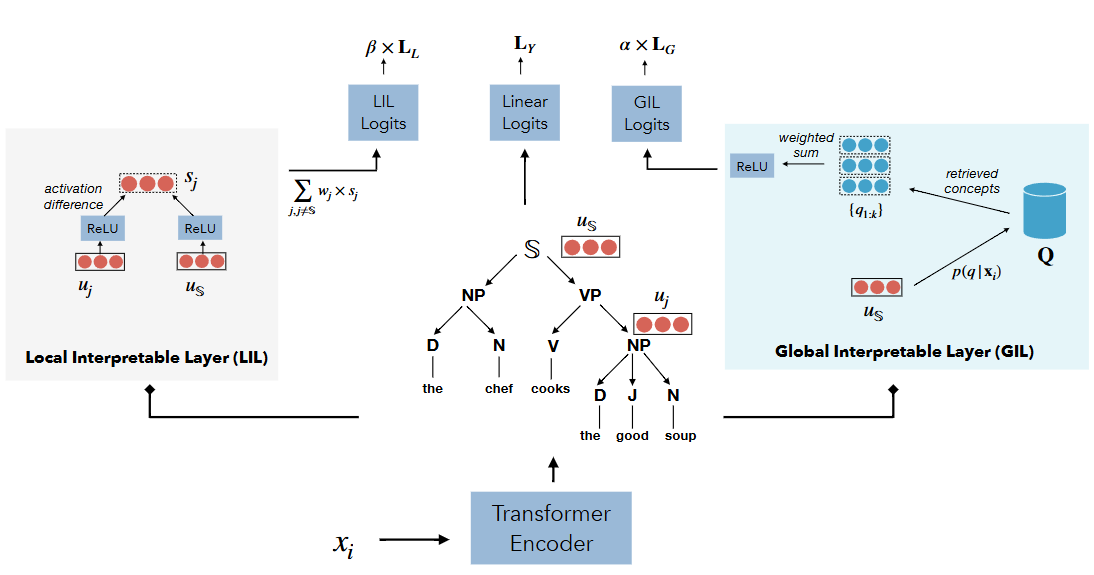
인코더 레이어:
- 입력 문장 $x_i$ 는 Transformer Encoder를 통해 인코딩되어 단어별 표현 $\{h_i\}$ 와 구문 트리의 각 구성 요소(예: 명사구 NP, 동사구 VP 등)의 표현 $u_j$ 가 만들어집니다.
Linear Logits (중앙):
- 문장 전체 표현 $u_S$ 를 기반으로 한 최종 분류 레이어 출력입니다.
- 최종 분류 손실 $L_Y$ 로 학습됩니다.
Local Interpretable Layer (LIL) (왼쪽):
- 각 구(phrase) $u_j$ 와 전체 문장 표현 $u_S$ 를 ReLU 활성화 함수에 통과시켜 $s_j$ 를 얻습니다.
- $s_j$ 는 $u_j$ 가 제외된 문장 표현에 대응하는 값으로, 해당 구의 기여도를 'activation difference'를 통해 정량화합니다.
- 각 구의 기여도(중요도)에 가중치를 곱해 더한 값이 LIL Logits로 이어져, $\beta \times L_L$ 손실로 적용됩니다.
Global Interpretable Layer (GIL) (오른쪽):
- Training set에서 추출된 개념(구)들의 저장소 $Q$ 가 있습니다.
- 입력 문장 표현 $u_S$ 와 $Q$ 내 개념 벡터들과의 내적을 통해 코사인 유사도를 계산, 내적 최대 검색(Maximum Inner Product Search, MIPS)으로 상위 $k$ 개의 영향력 있는 개념 $\{q_{1:k}\}$ 를 찾아옵니다.
- 이 개념들의 가중 합을 ReLU와 선형 계층에 통과시켜 GIL Logits를 계산, $\alpha \times L_G$ 손실로 사용합니다.

전체 손실함수

L = \alpha \times L_G + \beta \times L_L + L_Y

주요 목적: 클래스 예측의 조건부 로그 우도 (conditional log-likelihood)를 최대화합니다.
예측 레이어 포함: linear (레이블 예측용), LIL (Local Interpretability Layer), GIL (Global Interpretability Layer) 모두에서 각각의 출력에 대해 학습합니다.
정규화(regularization): LIL, GIL 레이어의 출력이 최종 태스크 성능 향상에 기여하도록 정규화합니다.
최종 손실 $L$ 는 세 부분의 가중 합이며, $\alpha, \beta$ 는 정규화 하이퍼파라미터.

각 손실함수에 대한 상세설명

linear 레이어의 레이블 예측 손실:
- $L_Y = -\sum_{c=1}^C y_c \log(l_{Y})$ 로, 레이블에 대한 크로스 앤트로피 로스
GIL 손실 $L_G$ :
- 훈련 데이터에서 상위 K개 개념 $q_1, q_2, ..., q_K$ 를 뽑아 가중합 $\sum_k w_k \times q_k$ 을 계산합니다.
- 이 때 각 가중치 $w_k$ 는 학습 가능한 파라미터입니다.
- 활성함수 $g = \mathrm{ReLU}$ 적용 후 선형변환 $W_u$ 및 바이어스 $b_u$ 를 거쳐 softmax로 확률 분포 $l_G$ 로 변환합니다.
- 크로스엔트로피 손실: $L_G = -\sum_{c=1}^C y_c \log(l_{G})$ 여기서 $y_c$ 는 정답 레이블의 one-hot 인코딩.
LIL 손실 $L_L$ :
- 각 local 개념 $s_j$ 에 가중치 $w_{s_j}$ 를 곱한 후 가중 합산 $l_L = \sum_j w_{s_j} s_j$ 을 계산합니다.
- 크로스엔트로피 손실: $L_L = -\sum_{c=1}^C y_c \log(l_{L})$ .

4. Experiments

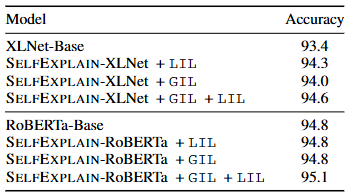
$K = 5, 10$ 일 때 큰 차이가 없었음.
$\alpha, \beta = {0.01, 0.1, 0.5, 1.0}$ 에서 튜닝.
LIL과 GIL가 상보적.
이후 내용은 추가 예정.

상솜공방

상어 인형을 좋아하는 사람

이전 포스트

InterFusion: Text-Driven Generation of 3D Human-Object Interaction

다음 포스트

SELFEXPLAIN: A Self-Explaining Architecture for Neural Text Classifier

논문 리뷰

1. Introduction

interpretability for neural text classification

post-hoc explanation model:

inherent interpretable model:

저자의 모델

LIL

GIL

2. SELFEXPLAIN

2.1 Defining human-interpretable concepts

수식

예시

2.2 Concept-Aware Encoder E

Concept에 대한 벡터 uju_juj​ 계산

예시

루트 노드에 대한 벡터 uSu_SuS​ 계산

2.3 Local Interpretability Layer (LIL)

개념

수식

코드 구현

코드와 수식 비교

1) 구문 임베딩 계산

torch.bmm() 연산의 예시

hidden_state (1, 5, 4)

nt_idx_matrix (1, 3, 5)

연산 과정

1번째 구문 임베딩:

2번째 구문 임베딩:

3번째 구문 임베딩:

결과

2) ReLU 활성화 적용

3) 문장 전체 임베딩(요약) 계산

4) 활성화 차이 계산

5) 구문별 분류(로짓) 계산

2.4 Global Interpretability layer (GIL)

개념

개념 저장소 Q

입력 샘플에 대한 영향력 있는 개념 선택

코드 구현

1) 입력 문장 임베딩

2) 개념 저장소

3) 유사도(내적) 계산

4) 상위 K개 개념 선택

5) 상위 K개 개념 벡터 추출

6) 입력 벡터와 개념 벡터 결합 및 멀티헤드 어텐션

예시 값

예시 결과

7) 최종 분류 레이어

8) 반환값

2.5 Training

모델 아키텍처

전체 손실함수

각 손실함수에 대한 상세설명

4. Experiments

InterFusion: Text-Driven Generation of 3D Human-Object Interaction

Diffusion Hyperfeatures: Searching Through Time and Space for Semantic Correspondence

0개의 댓글

Concept에 대한 벡터 $u_j$ 계산

루트 노드에 대한 벡터 $u_S$ 계산

`hidden_state` (1, 5, 4)

`nt_idx_matrix` (1, 3, 5)