[NLP] Transformer : Attention Is All You Need
0. 기존 모델의 한계점
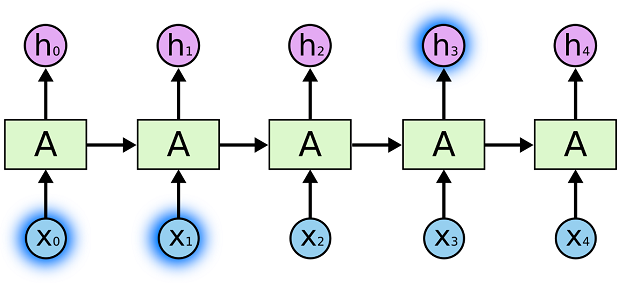
장기 의존성 문제(long-term dependacy) : RNN이 은닉 상태(hidden state)를 통해 과거의 정보를 저장할 때 문장의 길이가 길어지면 앞의 과거 정보가 마지막 시점까지 전달되지 못하는 현상
1. 트랜스포머의 등장
트랜스포머(transformer)는 RNN에서 사용한 순환 방식을 사용하지 않고 attention만을 사용한 모델
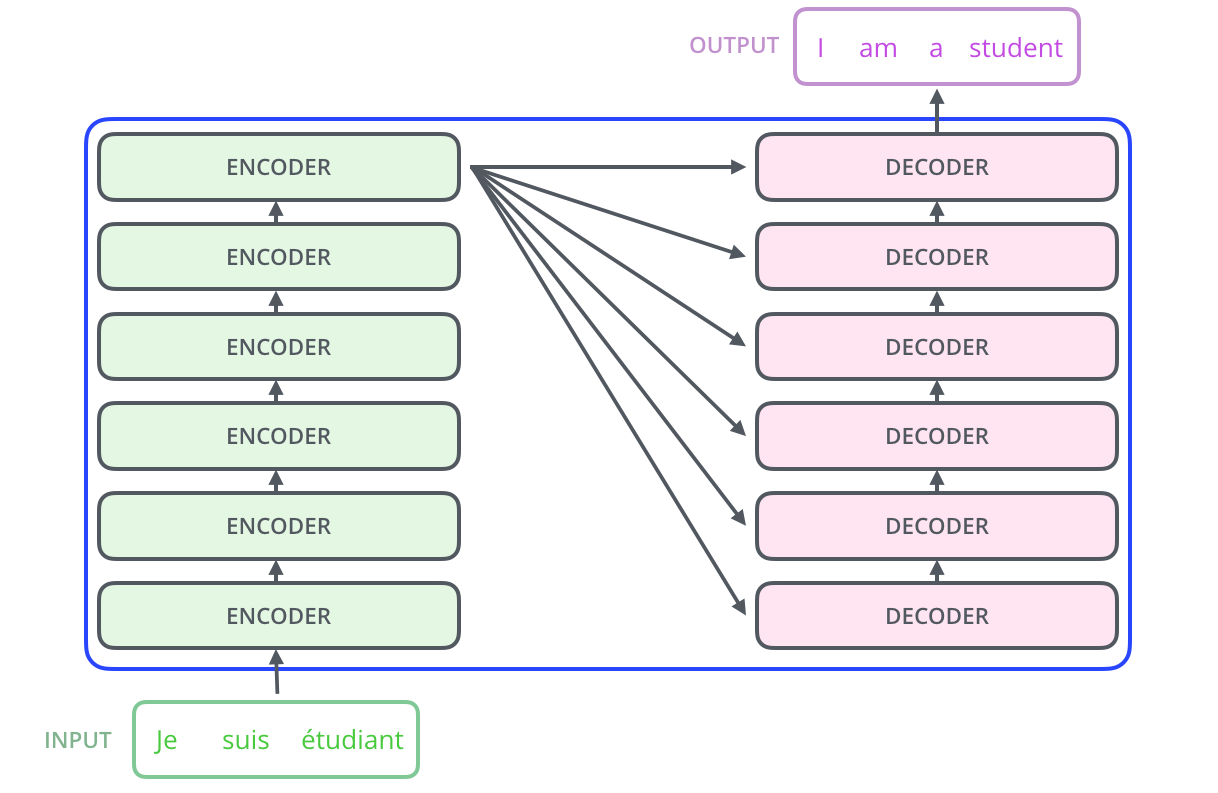
기계 번역 태스크에서의 트랜스포머의 작동
Encoder : 입력 문장을 입력하면 인코더는 입력 문장의 표현 방법을 학습사고 그 결과를 디코더에 전달한다.Decoder : 인코더에서 학습한 표현 결과를 입력받아 사용자가 원하는 문장을 생성한다.
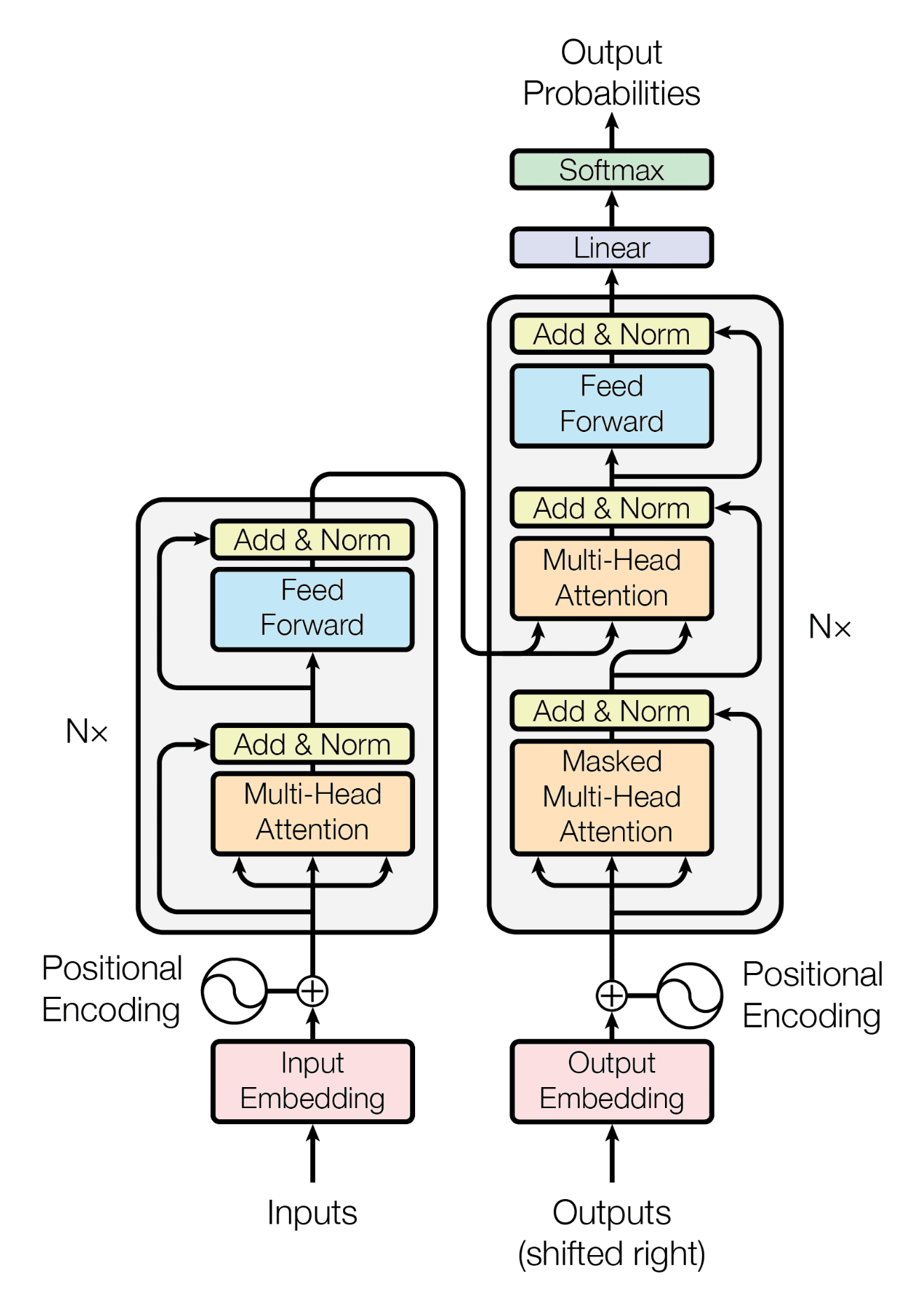
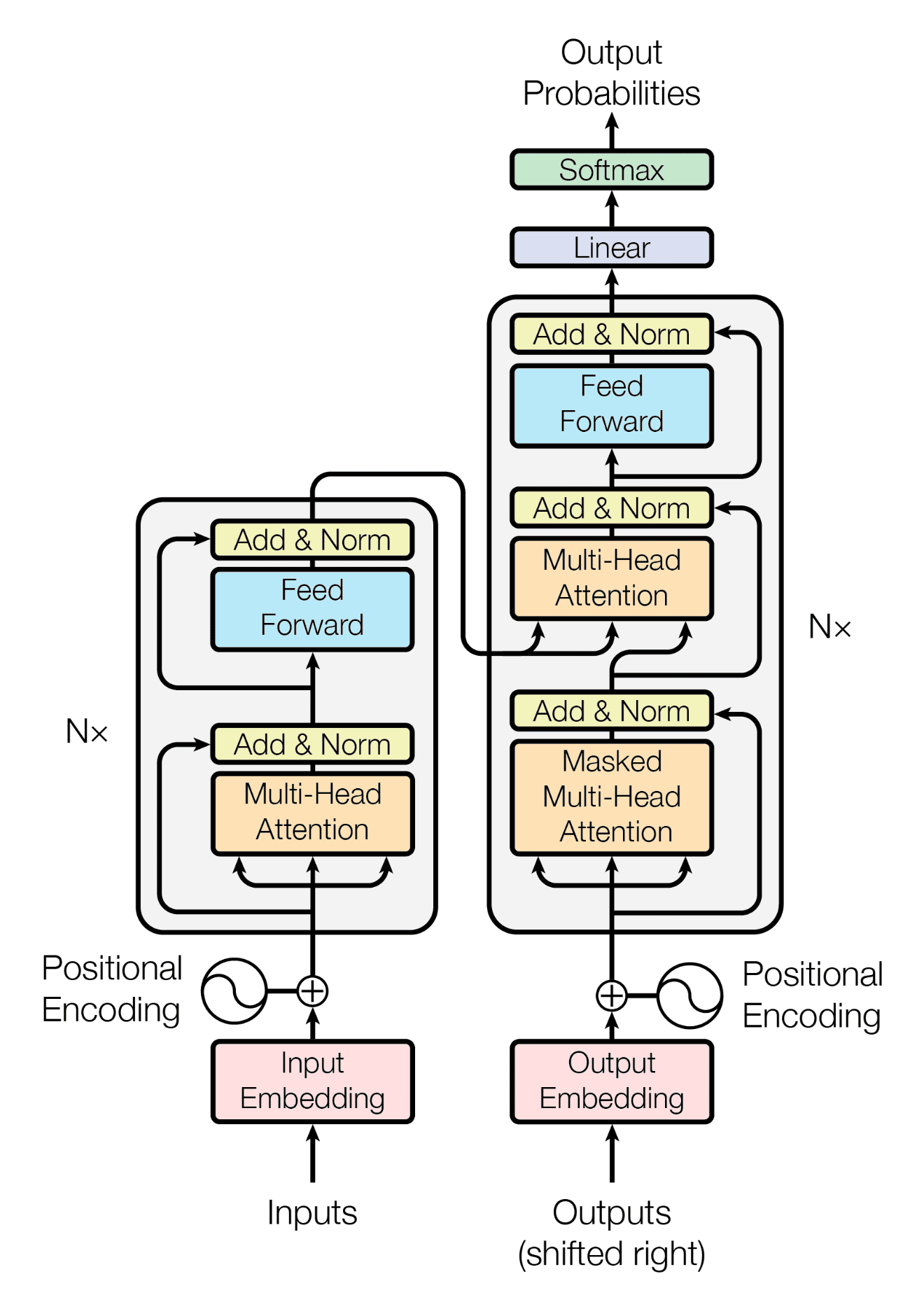
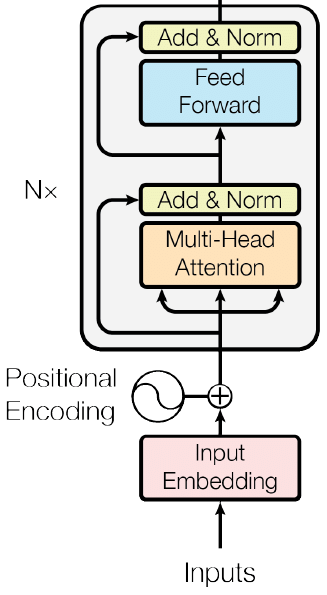
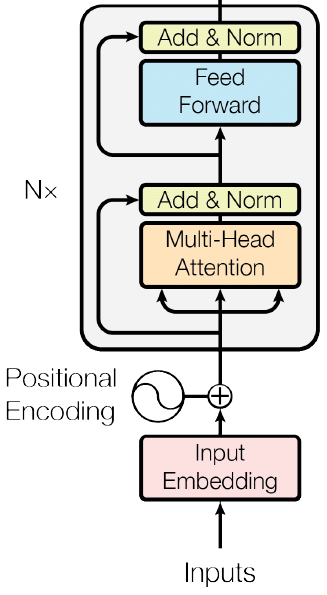
2-1. Encoder의 전체 구조
트랜스포머는 N개의 인코더가 쌓인 형태(논문에서 N = 6)
각 인코더의 결과값은 다음 인코더의 입력값으로 들어간다.
마지막 층에 있는 인코더의 결괏값이 입력값의 최종 표현 결과가 된다
Input : 입력 문장
Output : 입력 문장의 표현 결과
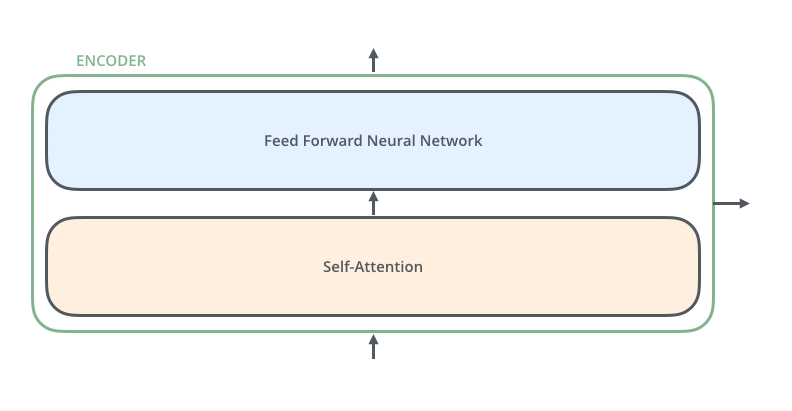
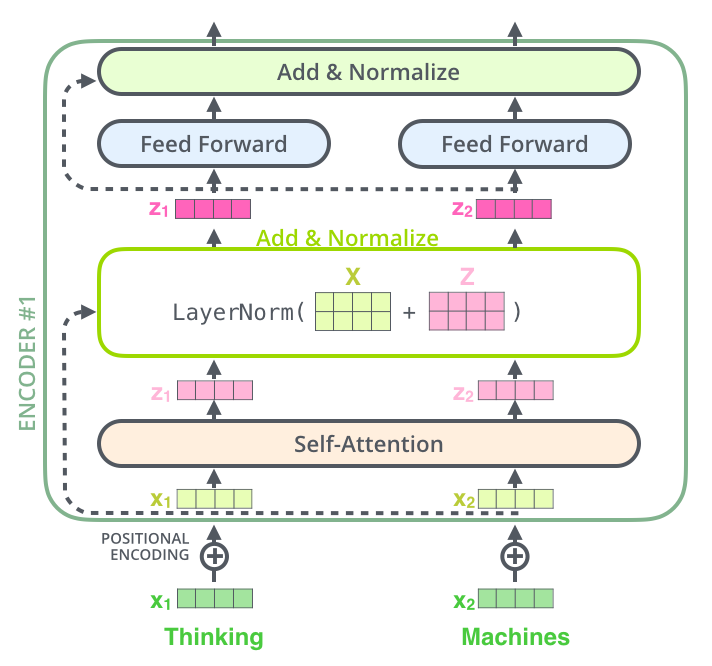
각 인코더 블록의 형태는 동일하며 인코더 블록은 2가지 요소로 구성된다.
Multi-Head Attention(Self-Attention)Feed Forward Neural Network
Multi-Head Attention을 이해하기 위해서는 Self-Attention의 동작 원리를 알아야한다.
2-2. Self-Attention
입력 문장이 들어왔을 때 각각의 단어의 표현을 계산하는 동안 각 단어의 표현들은 문장 안에 있는 다른 모든 단어의 표현과 연결되어 단어가 문장 내에서 갖는 의미를 이해한다.
‘I am good’ 이라는 입력 문장이 주어졌을 때 우선 각 단어의 임베딩(Embedding)을 추출한다.
x i = [ 1.76 , 2.22 , . . . , 6.66 ] x_i = [ 1.76, 2.22, ..., 6.66] x i = [ 1 . 7 6 , 2 . 2 2 , . . . , 6 . 6 6 ] x a m = [ 7.77 , 0.631 , . . . , 5.35 ] x_{am} = [ 7.77, 0.631, ...,5.35] x a m = [ 7 . 7 7 , 0 . 6 3 1 , . . . , 5 . 3 5 ] x g o o d = [ 11.44 , 10.10 , . . . , 3.33 ] x_{good} = [11.44, 10.10, ..., 3.33] x g o o d = [ 1 1 . 4 4 , 1 0 . 1 0 , . . . , 3 . 3 3 ]
최종적으로 입력 문장을 임베딩하여 표현한 임베딩 행렬 X X X X = [ x i x a m x g o o d ] = [ 1.76 2.22 . . . 6.66 7.77 0.631 . . . 5.35 11.44 10.10 . . . 3.33 ] X = \begin{bmatrix} x_{i}\\ x_{am}\\ x_{good}\\ \end{bmatrix} = \begin{bmatrix} 1.76 & 2.22 & ... & 6.66\\ 7.77 & 0.631 & ... & 5.35\\ 11.44 & 10.10 & ... & 3.33\\ \end{bmatrix} X = ⎣ ⎢ ⎡ x i x a m x g o o d ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 1 . 7 6 7 . 7 7 1 1 . 4 4 2 . 2 2 0 . 6 3 1 1 0 . 1 0 . . . . . . . . . 6 . 6 6 5 . 3 5 3 . 3 3 ⎦ ⎥ ⎤
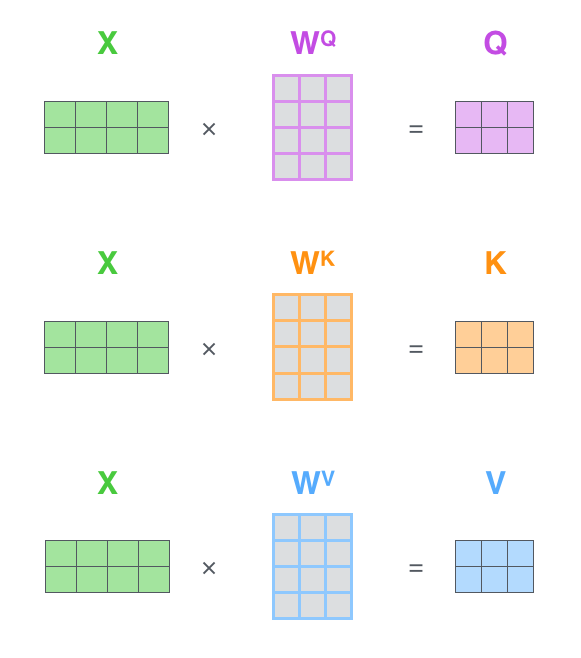
입력 행렬 X X X Q Q Q K K K V V V W Q W^Q W Q W K W^K W K W V W^V W V Q Q Q K K K V V V W W W
Q Q Q K K K V V V q 1 q_1 q 1 k 1 k_1 k 1 v 1 v_1 v 1 X W Q = [ x i x a m x g o o d ] W Q = [ 3.69 7.42 . . . 4.44 11.11 7.07 . . . 76.7 99.3 3.69 . . . 0.85 ] = [ q i q a m q g o o d ] = Q XW^Q= \begin{bmatrix} x_{i}\\ x_{am}\\ x_{good}\\ \end{bmatrix} W^Q = \begin{bmatrix} 3.69 & 7.42 & ... & 4.44\\ 11.11 & 7.07 & ... & 76.7\\ 99.3 & 3.69 & ... & 0.85\\ \end{bmatrix} = \begin{bmatrix} q_{i}\\ q_{am}\\ q_{good}\\ \end{bmatrix} = Q X W Q = ⎣ ⎢ ⎡ x i x a m x g o o d ⎦ ⎥ ⎤ W Q = ⎣ ⎢ ⎡ 3 . 6 9 1 1 . 1 1 9 9 . 3 7 . 4 2 7 . 0 7 3 . 6 9 . . . . . . . . . 4 . 4 4 7 6 . 7 0 . 8 5 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ q i q a m q g o o d ⎦ ⎥ ⎤ = Q 이제 Self-Attention이 Q Q Q K K K V V V
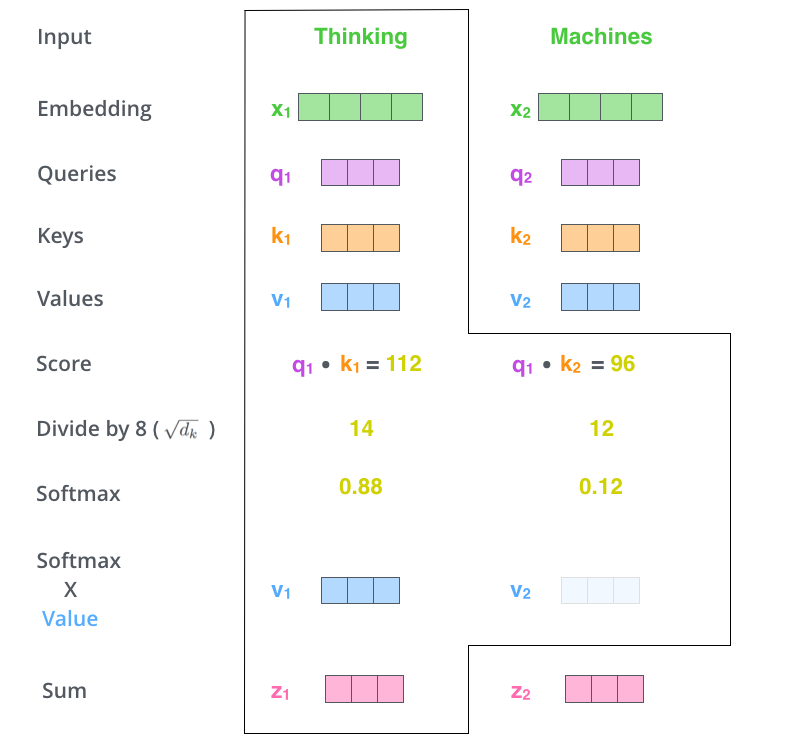
Q Q Q K K K Q K T = [ q i q a m q g o o d ] [ k i k a m k g o o d ] = [ q i k i q i k a m q i k g o o d q a m k i q a m k a m q a m k g o o d q g o o d k i q g o o d k a m q g o o d k g o o d ] = [ 110 90 80 70 99 70 90 70 100 ] QK^T = \begin{bmatrix} q_{i}\\ q_{am}\\ q_{good}\\ \end{bmatrix} \begin{bmatrix} k_{i} & k_{am} & k_{good}\\ \end{bmatrix} = \begin{bmatrix} q_{i}k_{i} & q_{i}k_{am} & q_{i}k_{good}\\ q_{am}k_{i} & q_{am}k_{am} & q_{am}k_{good}\\ q_{good}k_{i} & q_{good}k_{am} & q_{good}k_{good}\\ \end{bmatrix} = \begin{bmatrix} 110 & 90 & 80\\ 70 & 99 & 70\\ 90 & 70 & 100\\ \end{bmatrix} Q K T = ⎣ ⎢ ⎡ q i q a m q g o o d ⎦ ⎥ ⎤ [ k i k a m k g o o d ] = ⎣ ⎢ ⎡ q i k i q a m k i q g o o d k i q i k a m q a m k a m q g o o d k a m q i k g o o d q a m k g o o d q g o o d k g o o d ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 1 1 0 7 0 9 0 9 0 9 9 7 0 8 0 7 0 1 0 0 ⎦ ⎥ ⎤
Q Q Q K T K^T K T q i q_{i} q i k i , k a m , k g o o d k_{i}, k_{am}, k_{good} k i , k a m , k g o o d Q Q Q K T K^T K T Q Q Q K T K^T K T d k d_k d k Q K T d k = Q K T 8 = [ 13.75 11.25 10 8.75 12.375 8.75 11.25 8.75 12.5 ] \frac{QK^T}{\sqrt{d_k}} = \frac{QK^T}{8} = \begin{bmatrix} 13.75 & 11.25 & 10\\ 8.75& 12.375 & 8.75\\ 11.25 & 8.75 & 12.5\\ \end{bmatrix} d k Q K T = 8 Q K T = ⎣ ⎢ ⎡ 1 3 . 7 5 8 . 7 5 1 1 . 2 5 1 1 . 2 5 1 2 . 3 7 5 8 . 7 5 1 0 8 . 7 5 1 2 . 5 ⎦ ⎥ ⎤
This leads to having more stable gradients. 소프트맥스 함수를 사용해 정규화 작업을 진행하여 전체 값의 합이 1이 되며 각각 0과 1 사이의 값을 가지도록 한다.s o f t m a x ( Q K T d k ) = [ 0.90 0.07 0.03 0.025 0.95 0.025 0.21 0.03 0.76 ] softmax(\frac{QK^T}{\sqrt{d_k}}) = \begin{bmatrix} 0.90 & 0.07 & 0.03\\ 0.025 &0.95 & 0.025\\ 0.21 & 0.03 & 0.76\\ \end{bmatrix} s o f t m a x ( d k Q K T ) = ⎣ ⎢ ⎡ 0 . 9 0 0 . 0 2 5 0 . 2 1 0 . 0 7 0 . 9 5 0 . 0 3 0 . 0 3 0 . 0 2 5 0 . 7 6 ⎦ ⎥ ⎤
이러한 행렬을 스코어(score) 행렬이라고 하며, 이 점수를 바탕으로 문장 내에 있는 각 단어가 문장에 있는 전체 단어와 얼마나 연관되어 있는지 알 수 있다.
예를 들어, 스코어 행렬의 첫행을 보면 단어 ‘I’는 자기 자신과 90%, 단어 ‘am’과는 10%, 단어 ‘good’과는 3% 관련되어 있다는 것을 알 수 있다.
스코어 행렬과 밸류 행렬을 곱하여 Z Z Z Z = s o f t m a x ( Q K T d k ) V = [ 0.90 0.07 0.03 0.025 0.95 0.025 0.21 0.03 0.76 ] [ 67.85 91.2 . . . 0.13 13.13 63.1 . . . 0.025 12.12 96.1 . . . 43.4 ] = [ z i z a m z g o o d ] Z = softmax(\frac{QK^T}{\sqrt{d_k}})V= \begin{bmatrix} 0.90 & 0.07 & 0.03\\ 0.025 &0.95 & 0.025\\ 0.21 & 0.03 & 0.76\\ \end{bmatrix} \begin{bmatrix} 67.85 & 91.2 & ... & 0.13\\ 13.13 & 63.1 & ... & 0.025\\ 12.12 & 96.1 & ... & 43.4\\ \end{bmatrix}= \begin{bmatrix} z_{i}\\ z_{am}\\ z_{good}\\ \end{bmatrix} Z = s o f t m a x ( d k Q K T ) V = ⎣ ⎢ ⎡ 0 . 9 0 0 . 0 2 5 0 . 2 1 0 . 0 7 0 . 9 5 0 . 0 3 0 . 0 3 0 . 0 2 5 0 . 7 6 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 6 7 . 8 5 1 3 . 1 3 1 2 . 1 2 9 1 . 2 6 3 . 1 9 6 . 1 . . . . . . . . . 0 . 1 3 0 . 0 2 5 4 3 . 4 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ z i z a m z g o o d ⎦ ⎥ ⎤
z i = 0.90 ∗ v i + 0.07 ∗ v a m + 0.03 ∗ v g o o d z_{i} = 0.90 * v_{i} + 0.07 * v_{am} + 0.03 * v_{good} z i = 0 . 9 0 ∗ v i + 0 . 0 7 ∗ v a m + 0 . 0 3 ∗ v g o o d 어텐션 행렬은 각 점수를 기준으로 가중치가 부여된 벡터의 합을 계산한다.
2-3. Multi-Head Attention
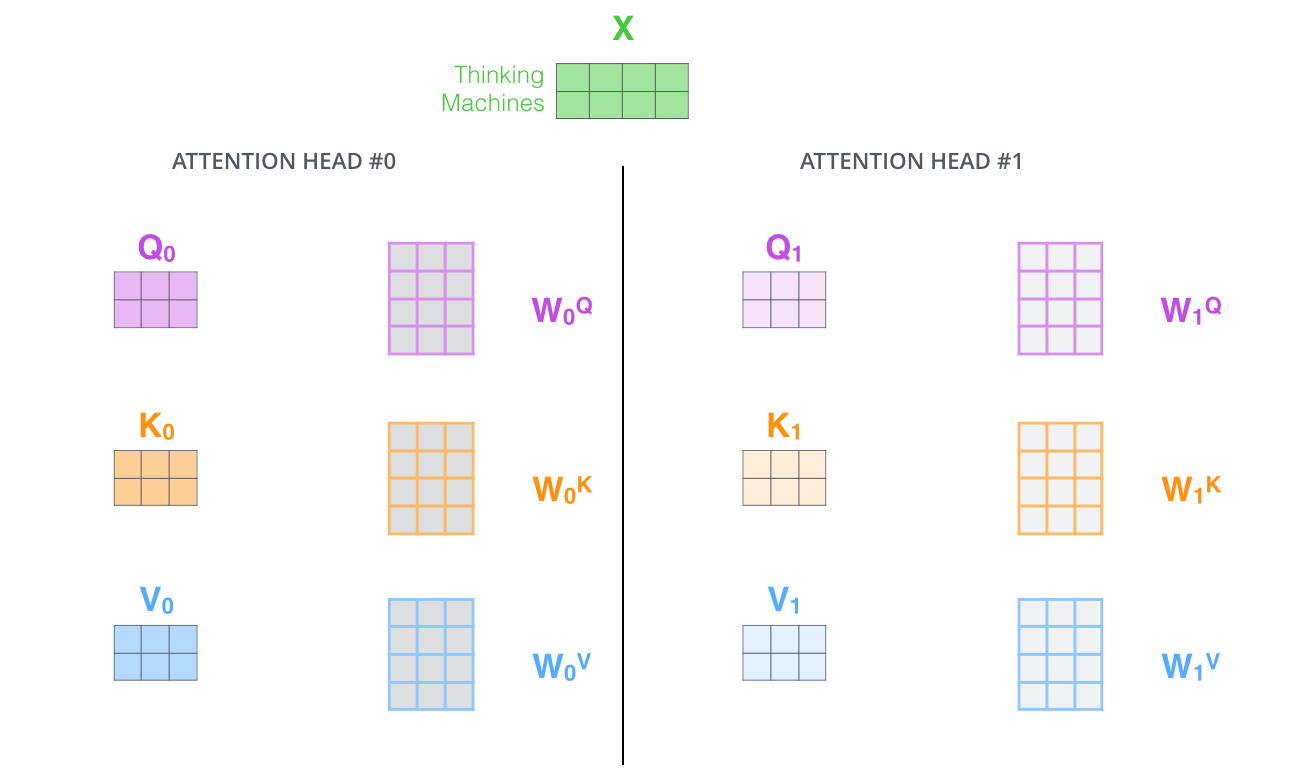
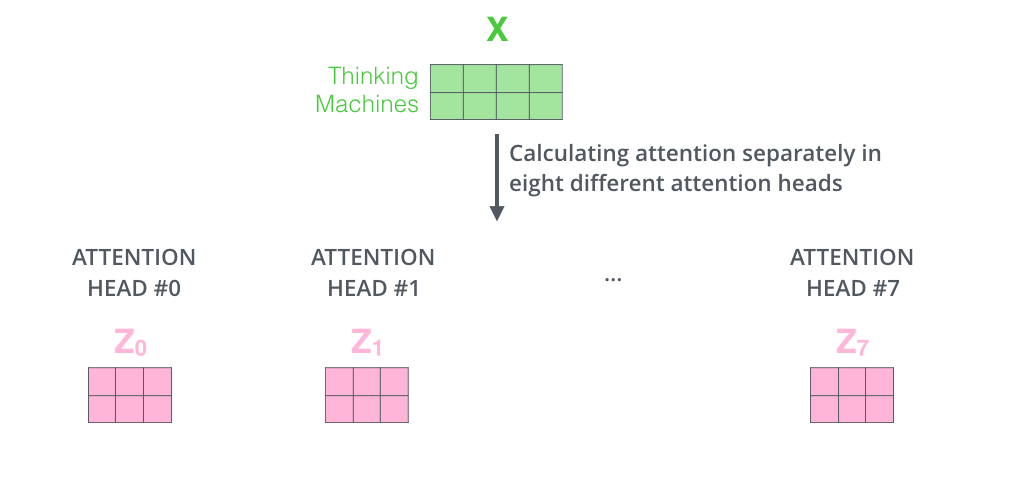
입력 문장의 토큰 간의 다양한 유형의 종속성 을 포착하기 위해 어텐션을 여러 개의 Head로 나눠서 병렬로 계산한다.
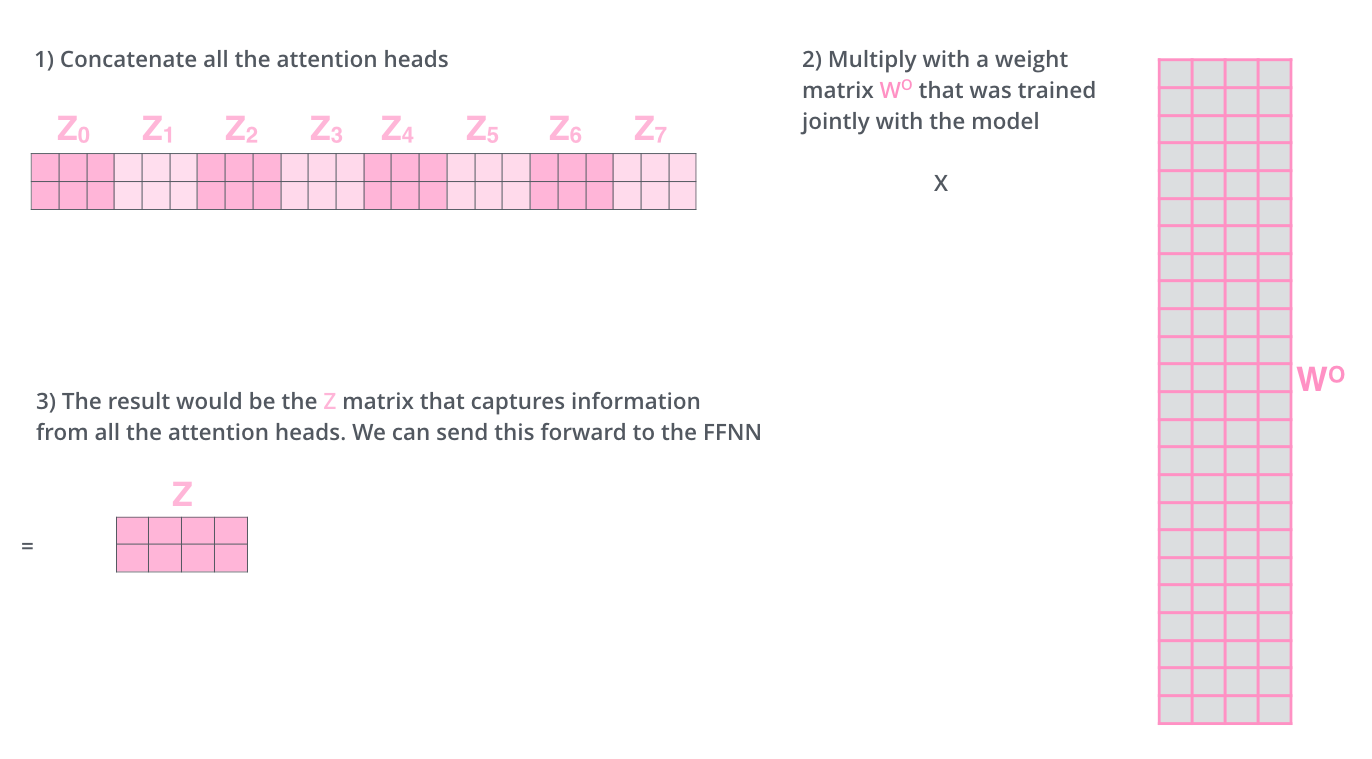
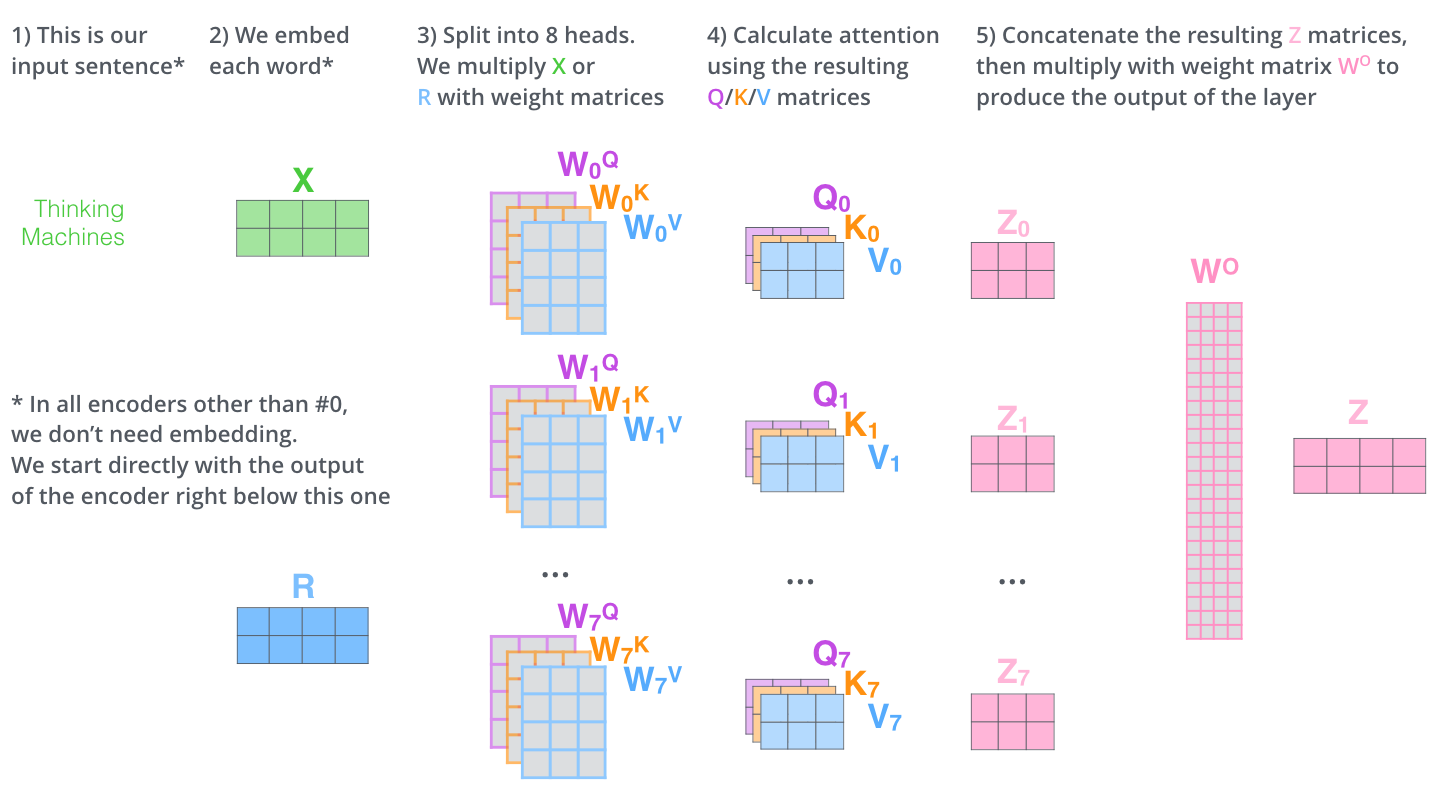
어텐션 결과의 정확도를 높이기 위해서 단일 헤드 어텐션(single-head attention)이 아닌 멀티 헤드 어텐션(multi-head attention)을 사용한 후 결괏값을 concat하는 형태로 진행한다.
h h h W o W^o W o Z Z Z h h h 어텐션 헤드의 최종 결과는 어텐션 헤드의 원래 크기이므로 크기를 줄이기 위해 가중치 행렬을 곱하는 것이다.
2-4. summary
첫번째 인코더 블록 외에는 입력에 대한 임베딩을 거치지 않아도 된다.
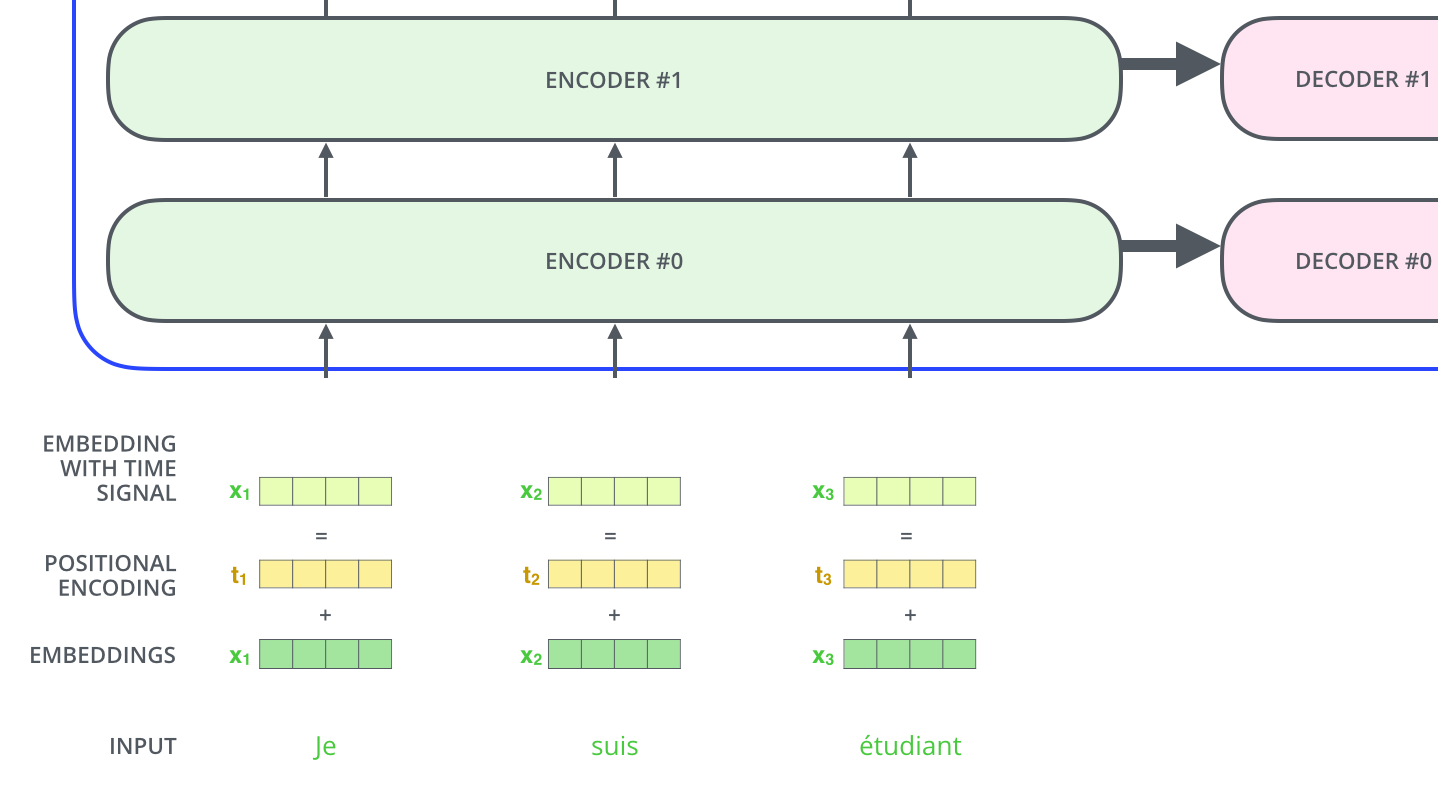
2-5. Positional Encoding
RNN의 경우에는 문장을 완전히 이해하기 위해 문장을 단어 단위로 나누어 입력한다.
Transformer의 경우에는 문장 안에 있는 모든 단어를 병렬 형태로 입력한다.
단어의 순서 정보가 유지되지 않은 상태에서 문장의 의미를 이해하기 어렵다.
위치 인코딩을 통해 각 단어의 순서(위치)를 표현하는 정보를 추가로 제공한다.
위치 인코딩 행렬 P P P X X X
입력 행렬 X X X P P P
2-6. Add & Normalize
레이어 정규화(Layer normalizaton)과 잔차 연결(residual connection)을 통해 다음과 같은 기능을 한다.
서브레이어(self-attention, feed forward)에서 Multi-Head Attention의 입력값과 출력값을 서로 연결한다.
서브레이어에서 Feed Forawrd의 입력값과 출력값을 서로 연결한다.
각각의 역할은 다음과 같다.
레이어 정규화(Layer normalizaton) :
텍스트의 길이는 가변적이기 때문에 입력값의 크기는 일정하지 않다.
따라서 input 기준으로 평균과 분산을 계산하는 레이어 정규화를 사용한다.
잔차 연결(residual connection) : X + s u b l a y e r ( X ) X + sublayer(X) X + s u b l a y e r ( X )
layer가 거듭되는 구조이기 때문에 gradient vanishing 문제를 보완하기 잔차 연결을 사용한다.
f ( x ) + x f(x) + x f ( x ) + x
2-7. Encoder summary
입력 문장을 임베딩 행렬(X ) X) X ) P ) P) P )
인코더 1은 입력값을 받아 Multi-Head Attention의 sublayer에 값을 보내고, Attention matrix(Z ) Z) Z )
출력된 어텐션 행렬에 residual connection과 Layer Norm를 진행하여 다음 서브레이어인 Feed Forward Network에 입력한다. → L a y e r N o r m ( X + Z ) LayerNorm(X + Z) L a y e r N o r m ( X + Z )
Feed Forward Network는 Attention matrix를 입력값으로 받아 인코더 표현을 결과값으로 출력한다.
인코더 1의 출력값을 그 위에 있는 인코더(인코더2)에 입력값으로 제공한다.
인코더 2에서는 이전과 동일한 과정을 거치고 최종적으로 인코더에서는 주어진 문장에 대한 표현 결과(R R R
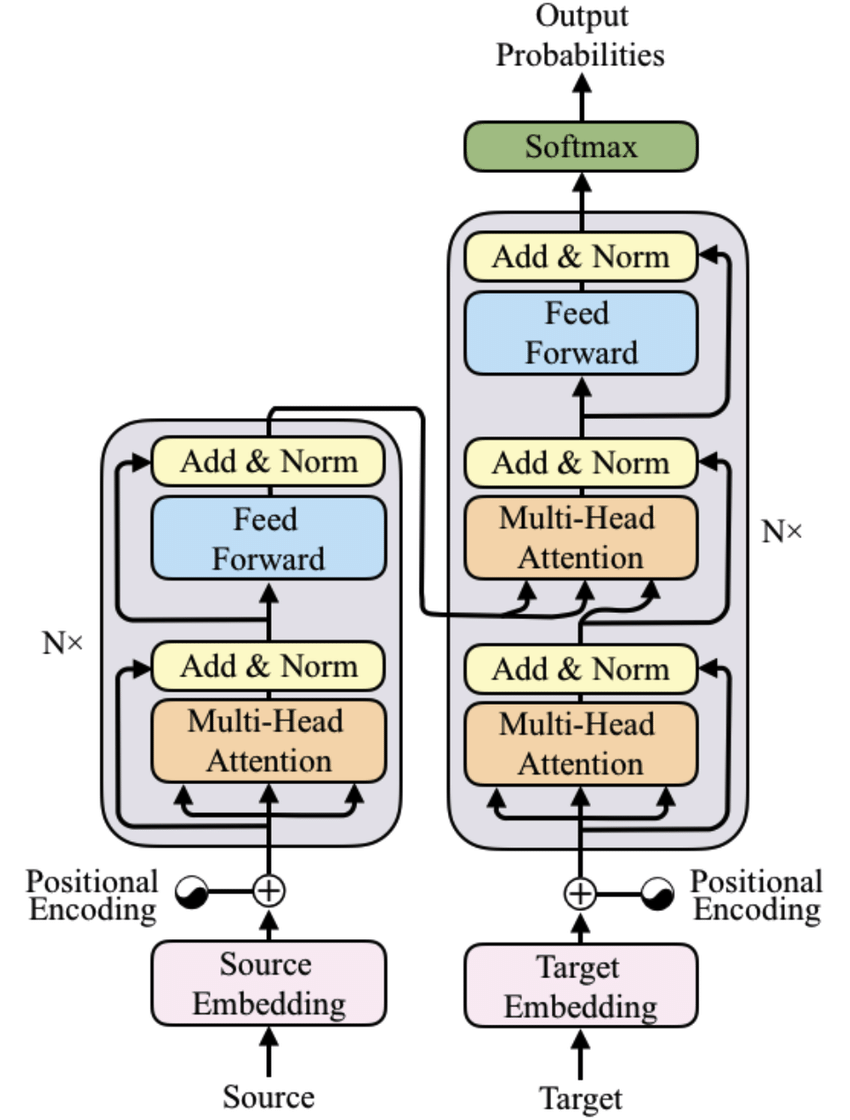
Encoder와 유사하게 Decoder 역시 N N N 디코더는 크게 3가지 서브 레이어로 구성되어 있다.
Masked Multi-Head AttentionMulti-Head Attention(Encoder-Decoder Attention)Feed Forward Network
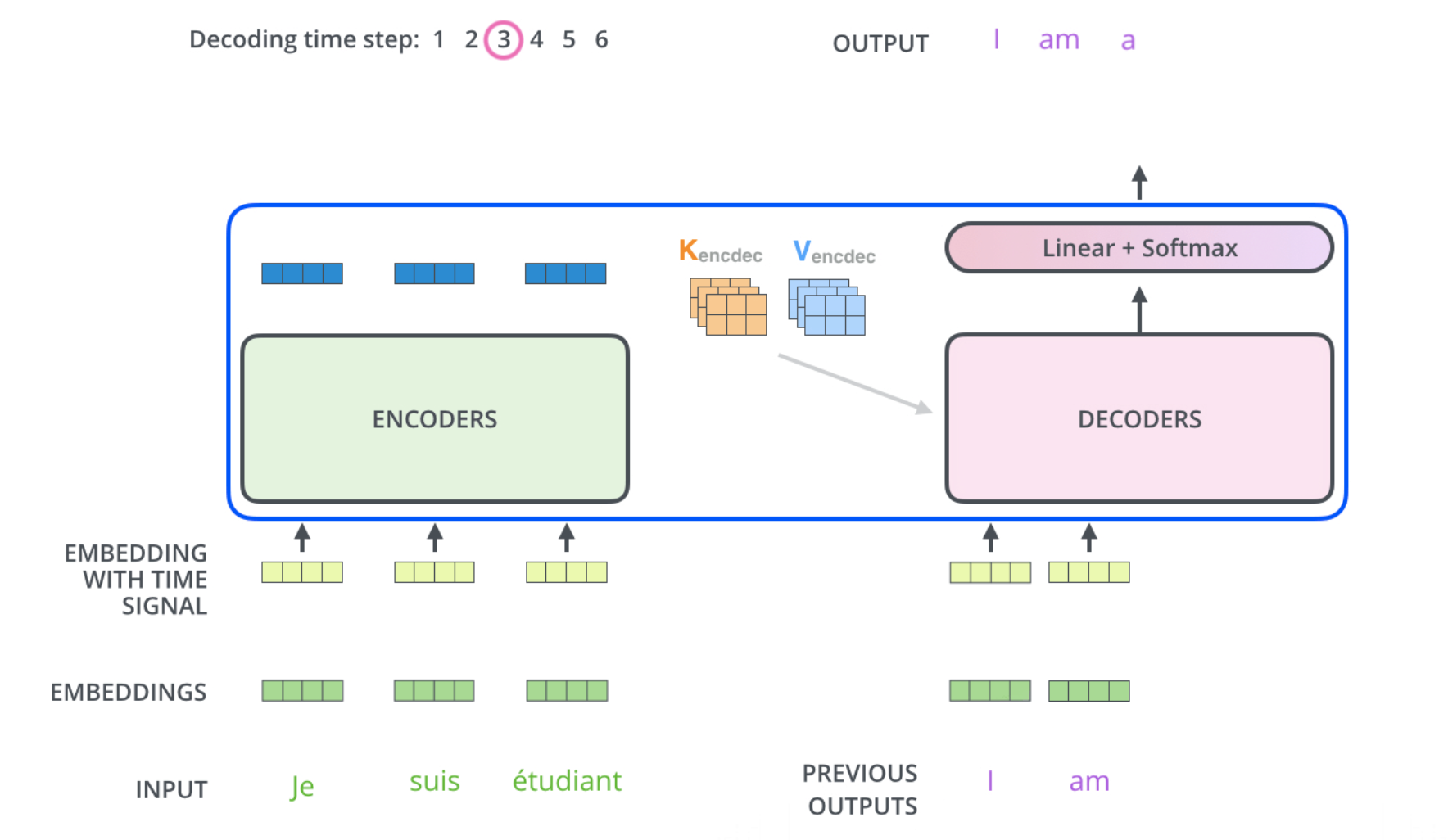
인코더의 출력값은 모든 디코더에서 사용되며 각 디코더는 이전 디코더의 입력값 과 인코더의 출력값 을 입력 데이터로 받는다.
모든 time step마다 디코더는 이전 time step에서 새로 생성한 단어를 조합하여 입력값을 생성하고 이를 이용해 다음 단어를 예측하는 방법을 진행한다.
처음에는 <sos> 토큰을 사용하며 <eos> 토큰을 생성할 때 타깃 문장의 생성은 완료된다.
디코더는 이전에 생성된 출력값을 입력값으로 생성할 때 위치 인코딩을 추가한 값을 디코더의 입력값으로 사용한다.
3-1. Masked Multi-Head Attention