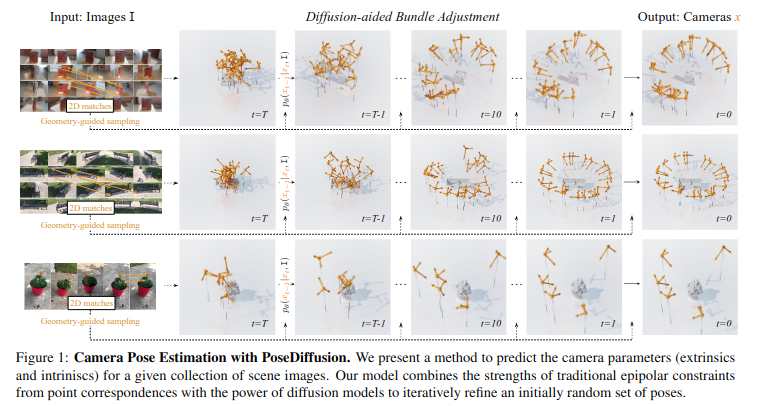
Overview

SfM problem을 probabilistic diffusion framework로 모델링하여, input 이미지들이 주어졌을 때 카메라 포즈를 conditional하게 모델링 진행. 다음과 같은 장점이 있다고 주장함: 1) 디퓨전 프로세스가 내재적으로 bundle adjustment의 반복적인 오차를 반영, 2) 에피폴라 기하학에서 유도된 기하 제약 조건을 매끄럽게 통합 가능, 3) 넓은 baseline을 가진 sparse view에도 조호은 성능을 보임, 4) 임의의 이미지들에 대해 intrinsic/extrinsic 추정이 가능.

SfM pipeline: Correspondences 추정 -> BA를 사용하여 모든 카메라를 reference 프레임에 대해 align. Incremental SfM의 경우 registered poses에서의 확장과 BA가 반복되어 진행.

Problem

아직 deep geometry 기반의 방법들중, sparse view에 대해 SfM을 제대로 하는 논문이 없었음. 이전 방법인 relpose는 dense-view를 핸들링하지 못함.

문제점	설명
1. 견고성 부족	기존 SfM은 견고한 keypoint 매칭에 의존하며, wide-baseline sparse view에선 성능 저하
2. 복잡한 최적화	Bundle Adjustment는 고차원에서 비선형 최적화를 수행하며 민감하고 계산 비용이 큼
3. 일반화 한계	학습된 SfM 시스템은 훈련된 데이터셋을 벗어나면 성능이 급감
4. 제한된 학습 기반 방법	기존 학습 기반 접근 (예: RelPose)은 회전만 예측하거나, 데이터 특화됨
5. 추론 불안정성	회전, 이동, 초점거리 등 연속적인 양을 직접 회귀하는 네트워크의 정확도가 낮음
6. 기존 SfM 구성요소 간 강한 상호의존성	Keypoint 탐지 → 매칭 → BA 최적화가 순차적으로 tightly coupled됨

Solution: POSE DIFFUSION

• Pose diffusion: 딥러닝과 corrosepondences 기반 제약 조건을 결합하여, sparse-view와 dense-view 모두에서 강인하게 작동. Bundle Adjustment (BA)를 해결하기 위해 디퓨전 프로세스를 도입.
  Modelling the probabil-ity p(x|I) of camera parameters x given observed images I

• $p(x|I)$를 학습시키기 위해, 카메라 pose가 알려진 대규모 이미지셋에서 학습을 진행. 학습 이후, Unseen된 sequence에 대해서, camera pose $x$를 $p(x|I)$ 추정을 통해 진행함.

• 디퓨전 모델은 복잡한 분포의 로그 가능도 공간(log-likelihood landscape)을 효율적으로 탐색할 수 있는 것으로 알려져 있으며, 이는 복잡한 BA(Bundle Adjustment) 최적화 문제와 매우 잘 맞는 방식.

해결방안	설명
1. 확산 모델 기반 Pose Sampling	카메라 포즈를 직접 회귀하는 대신, 확률분포 $p(x \| I)$에서 샘플링하여 추론 (diffusion 모델로 점진적 refinement)
2. Epipolar Constraint 기반 Guidance	학습된 denoiser의 출력을 2D 포인트 매칭에서 유도한 Sampson Epipolar Error로 보정하여 정확도 향상
3. Geometry-Guided Sampling (GGS)	Sampling 중 각 단계마다 기하학적 제약으로 추론을 유도함으로써 안정성과 정확도 개선
4. Intrinsics + Extrinsics 동시 추론	포즈뿐 아니라 초점 거리 등 카메라 내부 파라미터도 예측 가능
5. 학습 일반화 능력 강화	CO3Dv2 데이터셋으로 학습한 후 RealEstate10k 등 다른 도메인에서도 경쟁력 있는 성능을 보여줌
6. 효율적인 추론 구조	확산 모델은 병렬 학습이 가능하고, 사전 학습된 DINO 기반 이미지 feature 사용으로 효과적인 표현 가능

Details

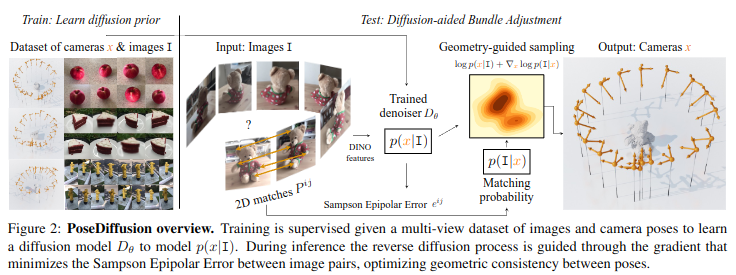
Detailed Problem setting

N개의 입력 이미지에 대해, camera parameter $x$를 추정하고자 함.

• Images: $I = (I^{i})^{N}_{i=1}$, Camera Params: $x = (x^{i})^{N}_{i=1}, x^{i}=(K^{i}, g^{i})$. (K:intrinsic, g: extrinsic)
• Given Images $I$, $p(x\|I)$를 통해 $p(x)$를 추정.

관점	Bundle Adjustment (BA)	Diffusion Process (in PoseDiffusion)
목적	카메라 포즈 및 3D 구조 최적화 (reprojection error 최소화)	카메라 포즈 분포 ( $p(x \|I)$ )에서 샘플링 (노이즈 제거하여 GT pose 복원)
초기화	초기 카메라 포즈/구조 필요 (SfM 매칭 기반)	무작위 포즈 $x_T \sim \mathcal{N}(0,I)$ 에서 시작
업데이트 방식	반복적 최적화 (Gauss-Newton, LM 등)	반복적 denoising (diffusion step-by-step refinement)
진행 과정	각 단계에서 residual/error를 줄이며 수렴	각 timestep에서 노이즈를 줄이며 pose 분포로 수렴
수학적 형태	비선형 least squares optimization	확률적 샘플링: $\; x_{t-1} \sim \mathcal{N}(\hat{\mu}_{t-1}, \Sigma_{t}) \;$
Guidance	Epipolar constraint, reprojection error	Sampson-guided sampling (epipolar geometry gradient)
수렴 결과	최적화된 카메라 intrinsics + extrinsics + 3D 포인트	노이즈 제거된 카메라 intrinsics + extrinsics
한계	초기화·outlier에 민감, local minima	확률적 탐색 가능 → global optimum에 가까움

Diffusion aided bundle adjustment

1. 학습 시
   • ground-truth의 이미지–카메라 파라미터 쌍 $(x_j, I_j)$ (j: 이미지내 패치 인덱스)을 사용해, 확산모델의 denosing process $D_{theta}$를 학습
   • 이 denoiser는 매 단계에서 노이즈가 추가된 카메라 파라미터를 점차 정교화해서 원래 값으로 복원하는 역할을 함.
2. 추론 시
   • 처음에는 완전히 무작위의 카메라 파라미터 $x_T ~ N(0,I)$을 샘플링하고, 학습된 Denoiser $D_{theta}$를 이용해 순차적으로 $x_T > x_{T-1} > ... > x_{0}$로 복원 진행. 최종적으로 예측된 $x_{0}$이 예측된 카메라 파라미터가 됨.
   • Denoiser로는 Transformer 기반 네트워크를 사용. 이미지 임베딩이 필요한데, DiNO를 사용하였다고 함.
     

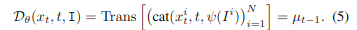
기존 BA	PoseDiffusion의 Diffusion-aided BA
반복적인 수치 최적화 필요 (2차 도함수 기반)	샘플링 기반으로 간단하게 최적화
초기화 민감 / 로컬 미니마 문제	확률적 탐색으로 global optima에 가까운 결과
고정된 알고리즘 구조	딥러닝으로 학습 가능한 범용성
모든 단계 연산 그래프 필요	역전파 없이 한 단계씩 학습 가능 (step-wise learning)

Geometry-Guided Sampling (GGS)

• PoseDiffusion은 diffusion 과정을 통해 노이즈가 낀 카메라 파라미터를 점점 정답에 가까운 상태로 복원
• 그러나 diffusion 모델은 회전(rotation), 위치(translation) 같이 정밀한 수치 추정에는 다소 부정확 -> two-view geometry constraint를 주어 정확도 향상
• 이를 위해 reliable 2D correspondences를 추출하여 DDPm sampling에 guide하여 epipolar 제약을 충족하도록 함.
• 각 diffusion sampling step에서, 현재 카메라 샘플 $x_t$를 기반으로 denoised 카메라 $D_{theta}(x_t, t, I)$를 생성하고, 이값을 epipolar geometry에 맞게 gradient를 통해 보정 진행

역할	설명
📌 샘플링 보정	Diffusion 샘플링 중 denoised 포즈에 기하학적 제약을 적용해 더 정확하게 유도
🧠 기초 개념	Epipolar constraint가 만족되도록 샘플을 gradient로 조정
⚙️ 사용 기술	Sampson error 계산 → gradient → denoised 포즈 보정
🎯 결과	기존 diffusion 단독보다 훨씬 더 정확한 카메라 포즈 추정 가능

< Sampson error와의 연관성 >

Result

• metric의 경우 회전 오차와, translation의 경우 정규화되어 scale을 못구하기 때문에 translation 벡터의 pred, gt간 각도 차이를 봄!