SVM (Support Vector Machine)

아래 그림과 같은 binary classification 문제를 가정해보자.

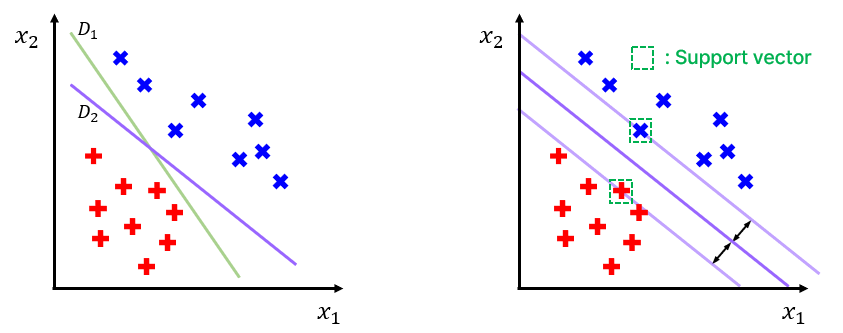
Fig 1. Binary classification, 이때 $x_1$ 과 $x_2$는 각각 data의 feature 이다.

우선 Fig 1. 의 왼쪽 그림에서, 초록색 선 $(D_1)$ 과 보라색 선 $(D_2)$ 중 어떤 선이 data point 들을 더 잘 구분하는가 물어본다면 아마 대부분 직관적으로 $D_2$ 를 고를 것이다. 이때 $D_1$ 이나 $D_2$ 같은 선을 decision boundary 라고 하는데, 데이터를 분류하는 기준 선 정도로 생각하면 된다.

SVM은 최적의 decision boundary를 정의하기 위한 모델이고, 이를 위해서는 decision boundary가 각 데이터 군집으로부터 최대한 멀리 떨어지도록 설정되어야 한다.

이때, support vector란 decision boundary와 가장 가까이 있는 data point를 의미한다.

Fig 1. 의 오른쪽 그림에서, decision boundary와 평행하도록 그어 support vector를 지나는 두 개의 선이 이루는 공간을 margin 이라고 부르는데, SVM은 적절한 decision boundary의 선택을 통해 margin을 가장 크게 만들어 분류를 수행하는 모델이라고 이해하면 된다.

이론적으로 neural network가 할 수 있는 것들을 모두 할 수 있기 때문에 deep learning이 주목받기 이전, 가장 인기있는 classifier 였고 (computational complexity 등의 관점에서 neural network 선호) 아래와 같은 특징이 있다.

SVM 특징

• 고차원 data에 대해서도 높은 성능을 보인다.
• Regression (회귀), ranking 등의 task에도 응용할 수 있다.
• Kernel을 설정하여 비선형 classification (분류)도 가능하다.

KNN (K-Nearest Neighbor)

KNN 알고리즘은 말 그대로 가장 가까운 $K$ 개의 data point들이 가진 정보를 통해 새로운 data를 예측하는 방법론을 의미한다.

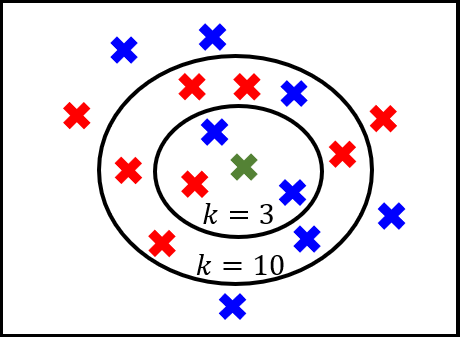
Fig 2. KNN algorithm where $K=3$, $K=10$.

Fig 2. 에서 초록색 data가 들어왔고, 이를 빨간색 (class) 혹은 파란색 (class) 로 분류해야하는 상황이라고 가정하자.

만약 $K=3$ 이면 새로운 data와 가장 가까운 $K$ 개 즉, 3개의 data point를 관찰하는데, 위의 예시에서 총 3개 중 2개는 파란색, 1개는 빨간색이므로 초록색 data는 파란색으로 분류된다.

$K=10$ 인 경우에도 $K=3$ 일때와 같이 $K (=10)$ 개의 이웃하는 point들을 보면, 빨간색이 6개, 파란색이 4개이기 때문에 이 경우에는 초록색 data가 빨간색으로 분류된다.

KNN 특징

• Fig 2. 에서 확인한 바와 같이 $K$ 값에 따라 성능이 크게 달라진다. $(K=3$ 일때는 파랑, $K=10$ 일때는 빨강$)$
• 직관적이며 결과 해석이 쉽다.
• 딱히 학습이 필요하지 않고, 간단하다.

Evaluation metrics

Confusion matrix

Binary classification ('Positive' or 'Negative') 을 가정했을 때, 실제 값과 예측 값 사이의 관계는 아래와 같이 총 4 가지 경우로 구분해볼 수 있다.

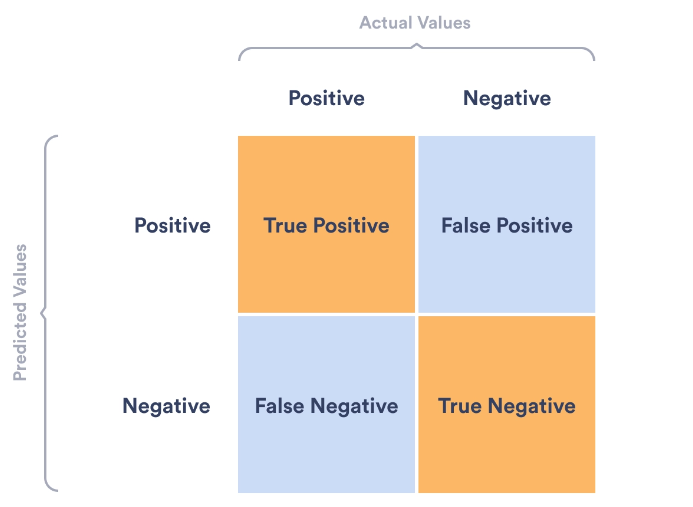
Fig 3. Confusion matrix.

Fig 3. 을 보면 결국, 파란색으로 색칠한 영역이 잘못된 예측을 한 경우이다. 각각을 case 별로 정리하면 아래와 같다.

True Positive: Positive 로 예측했고, 실제로 Positive (정답)
True Negative: Negative 로 예측했고, 실제로 Negative (정답)
False Positive: Positive 로 예측했는데, 실제로는 Negative
False Negative: Negative 로 예측했는데, 실제로는 Positive

False Positive $\Rightarrow$ Type 1 error

False Negative $\Rightarrow$ Type 2 error

이와 관련하여 다음의 예시를 보자.

1,000 개의 data를 이용하여 KTX의 지연 여부를 예측하는 상황을 가정. (정시 = 지연 X)

• (예측) 640 편 지연, 360 편 정시
• (실제) 250 편 지연, 750 편 정시

이때, 분류가 잘 되었는지를 확인하기 위해서는 confusion matrix를 구성하는 것이 좋다. 구성해보니 아래와 같았다고 보자.

True Positive (TP): 250
True Negative (TN): 360
False Positive (FP): 390
False Negative (FN): 0

Accuracy

Accuracy는 전체 데이터 중 제대로 분류한 데이터의 비율 즉, 모델이 얼마나 정확한 분류를 했는지에 대한 지표이다.

분류 모델의 성능을 평가하는 지표로 흔히 사용되기는 하지만, class의 분포가 불균형할 경우에는 신뢰성 있는 지표가 될 수 없다는 단점이 있다.

예를 들어, 10만개의 data 중 nagative가 2만개, positive가 8만개라고 하면 해당 data에 대해 positive라고만 대답하는 경우 accuracy가 0.8 이라는 높은 값을 얻게 된다.

즉 모델의 성능을 객관적으로 판단할 수 있는 지표가 되지 못하는 경우가 생긴다. (= 다른 평가 지표도 고려해야 한다.)

Precision

Precision은 positive로 예측한 data 중에서, 진짜 positive 였던 data가 얼마나 있었는지를 알려주는 지표이다.

이는 Negative 정보가 중요한 경우, 즉 실제로 negative인 data를 positive로 잘못 판단하면 위험한 경우에 유용한 지표가 된다.

가장 유명한 예시로는 스팸 메일 구분이 있는데 수신한 메일이 스팸이면 positive, 아니라면 negative로 분류한다고 보면, 스팸이 아닌 메일을 스팸으로 잘못 분류하였을 때 중요한 메일을 받지 못하는 상황이 생길 수 있다.

Recall (=TPR)

Recall은 precision과 반대되는 개념으로, Positive 정보가 중요한 경우, 즉 실제로 positive인 data를 negative로 잘못 판단하면 안되는 경우에 유용한 지표가 된다.

이때의 예시로는 암으로 의심되는 환자에 대해 암 검사를 하는 경우 암이 있다면 positive, 없다면 negative라고 했을 때, 실제 positive 인 사람이 negative로 잘못 분류된다면 생명에 큰 악영향을 줄 것이다.

FPR

FPR (=False Positive Rate)은 실제 negative인 data 중, 모델이 positive로 잘못 분류한 data의 비율을 의미하는 지표이다.

이때 주목할 점은 FPR과 TPR은 trade-off 관계에 있다는 것이다. 이는 FPR을 낮추고자 하면 TPR도 낮아질 수 밖에 없고, TPR을 높이고자 하면 FPR도 높아진다는 의미이다.

앞서 설명한 지표들을 KTX 예제에 적용하면 다음과 같다.
Accuracy = $610 / 1000$
Precision = $250 / 640$
Recall = $250 / 250$
FPR = $390 / 750$

정리하면, 상황에 따라 중요한 평가 지표가 다르기 때문에 적절한 평가 지표를 적용하여 결과를 해석할 수 있어야 한다.

Reference

Fig 3. https://plat.ai/blog/confusion-matrix-in-machine-learning/