
1. Four basic counting principles
(1) Addition principle(합의 원리)
Sample space의 크기(카디널리티)를 구할 때, S를 dijoint 한 파트 S1, S2, S3, ... Sm 로 분해 후 합으로 표시 (partitioning 할 때만 합의 원리가 적용됨)
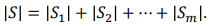
(2) Multiplication principle(곱의 원리)
집합 내 원소들이 단원소가 아닌 순서쌍(a, b)으로 구성되어 있을 때, a는 크기가 p인 집합에 속하고, b는 크기가 q인 집합에 속한다고 가정하면
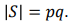
(3) Substraction principle(차의 원리)
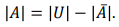
(4) Division principle(나누기의 원리)
모든 partioning 된 k개의 부분들의 크기가 각각 동일하다고 가정 시,
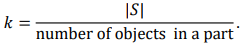
2. Permutations of sets
permutation = ordered arrangement. 보통 linear permutation 임
- notation : P(n, r) = n x (n-1) x ... x (n-r +1). -> r개
예제1 : 1~15를 4-by-4 grid 의 빈 칸에 넣을 때의 경우의 수는?
-> P(16, 15)예제2 : 26개의 알파벳 중 모음 a, e, i, o, u는 인접하지 않게 배열하는 방법은?
21개의 자음을 세워놓고 모음이 들어갈 경우,
맨앞과 맨뒤를 제외하고 22개의 공간이 만들어진다.
그 중 5개의 모음을 세우면 P(22, 5) 이며 각각의 자음 배열도 바꾸면 최종적으로는
21! x P(22, 5)가 된다.예제3 : 1~9를 사용하여 7자리 수를 만들되, 5와 6이 연속으로 나오지 않는 경우는?
차집합을 이용한다. 즉, '전체 경우 - 5와 6이 연속으로 나오는 경우' 로 계산한다.
7개의 공간에 9개를 순열시키는 것 : P(9, 7 )
7개의 공간 중 연속된 두 공간을 점하고 있다고 가정하고 7개의 수를
순열시키는 것 : P(7, 5)
점한 두 공간이 있을 수 있는 위치 : 6
두 공간 끼리의 순열 : 2!
-> P(9, 7) - { 2! x 6 x P(7, 5) }- Circullar r-permutation (원순열 )
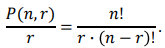
예제4 : 돌아가는 원판에서 12개의 다른 마크들이 배열될 수 있는 경우의 수는?
P(12, 12) / 12 = 11!예제5 : 10명의 사람을 원탁에 앉히는데 A, B는 서로 인접해서 앉기를 꺼릴 경우의 수는?
마찬가지로 차집합을 이용하여 계산한다.
10!/10 - 2 x 8! = 7 x 8! 예제6 : 6개의 구슬을 목걸이로 꿰멜 수 있는 가지 수는?

*중요 : 목걸이는 뒤집어도 같은 배열로 취급됨.
6!/6 x 1/23. Combinations of sets
combination = unordered selection
r-combination = r-subsets
-
notation : C(n, r) = P(n,r) / r! = n! / {r!(n-r)!}
-
Pascal's formula
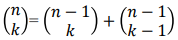
n개의 전체집합 중 k개의 부분집합을 뽑을 수 있는 가지 수. (1 <= k <= n-1 로 가정) -
partion 문제로 접근 시
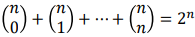
예제7 : 25개의 점 중 3개의 점을 뽑을 때, 도형의 개수는?
-> C(25, 3)
예제8 : 15명 중 12명이 들어왔는데, 그 12명이 25개의 좌석에 임의로 앉는 경우의 수는?
-> C(15, 12) x P(25, 12)
예제9 : 26개의 알파벳으로 8자리 단어를 만들 때, 3개의 모음, 4개의 모음, 5개의 모음이 들었을 경우의 수는? (중복을 허락함)
모음이 3개인 경우 : C(8, 3), 모음 5개 중 중복해서 3공간에 넣는 경우 : 5^3
자음 21개를 남은 5 공간에 중복해서 넣는 경우 : 21^5
-> C(8, 3) x 5^3 x 21^ 5
따라서 모든 경우의 수는
{ 5^3 x 21^5 } x { C(8,3) + C(8,4) + C(8,5) }예제10 : n개의 전체집합 중 2개를 골라내는 가지 수는 P(n,2) / 2! 인데, 다음을 증명하시오
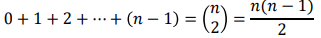
partioning이 필요하다. 2개 중 큰 값을 i, 작은 값을 j라고 가정 시,
i=1 일경우 j=0이되는데 그런 경우는 없으므로 좌변의 0인 상황이다.
i=2 -> j=1 이므로 1가지 경우가 있고
i=3 -> j=1, j=2 이므로 2가지 경우
i=4 -> j=1, j=2, j=3 이므로 3가지 경우가 있다.
i=n -> j=1, j=2, ... , j=n-1 으로 n-1d의 경우가 있으므로
이를 모두 더하면 위 등식이 성립함을 알 수 있다. 4. Permutations of multisets
multiset : 집합 내에 중복된 원소도 허용
- k개의 서로 다른 것들이 중복이 허락되는 상태에서 k보다 큰 n개만큼 들어있는 집합에서
어떤 원소가 최대 몇개 까지 허용되는가 ? : repetition number (반복수)
대부분은 infinite repetition number를 가짐(가장 쉬운 경우) -> K^r
예제11 : 3진수(termary numerals) 0, 1, 2 를 이용하여 4자리 수를 만들어라
multiset : {무한 * 0, 무한 * 1, 무한 * 2 } = {4 * 0, 4 * 1, 4 * 2}
-> 3^4 = 81- Multinomial coefficient (다항계수) : n1, n2, ... nk (여기서 숫자는 finite repetition number) 일 때, 모든 원소 n개를 다 골라서 배열할 수 있는 n-permutation의 수는?

예제12 : MISSISSIPPI 문자들의 permutation을 이용하여 만들 수 있는 단어의 개수는?
14! / (1! 4! 4! 2! ) -> {1 * M, 4 * I, 4 * S, 2* P} 예제13 : {a, b, c ,d }를 각각의 size 가 2인 set로 분리하라. label 화(red, blue로)된 경우와 아닌 경우는 ?
unlabel : {a ,b} ,{c, d}; {a, c}, {b, d}; {a, d}, {b, c}
label : red {a, b}, blue {c, d}; blue {a, b}, red {c, d}..
-> unlabel 의 part를 2가지씩 있다고 가정하여 총 6가지가 된다.- n = n1 + n2 + ... + nk이고 label화 되어있을 경우, n을 k개의 박스들로 partition 하는 경우의 수는 다음과 같다.
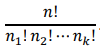
반면, n1= n2 = ... = nk 이고 not label 화 되어있을 경우는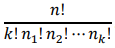
예제14 : 체스에서 똑같은 색의 8개의 rook (직선으로만 쭉 가는 말)이 서로 공격 못하는 위치(같은 행이나 열에 있으면 안됨)에 있을 경우의 수는?
1행 : 1번째 rook -> 8개의 칸에 존재 가능
2행 : 2번째 rook -> 7
...
8행 : 8번째 rook -> 1
즉 8! 의 경우의 수가 존재
예제14_1 : 서로 다른 8개의 rook일 경우
-> 8! x 8!
예제14_2 : 1개의 red, 3개의 blue, 4개의 yellow 가 있을 경우
-> 8! x 8! /(1!3!4!)
- 위 문제를 Theorem으로 나타내면,
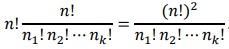
만약, finite repetition number의 경우 위와 같은 식을 도출하기 어려움 (예제 15번 처럼 가끔 예외적으로 풀기 쉬운 경우가 있음)
예제15 : S = {3 x a, 2 x b, 4 x c} , 이 9개 중 8개를 선택하여 8-permutation 을 만들면?
(1) {2 * a, 2 * b, 4 * c} 일 경우 : 8!/(2!2!4!)
(2) {3 * a, 1 * b, 4 * c} 일 경우 : 8!/(3!1!4!)
(3) {3 * a, 2 * b, 3 * c} 일 경우 : 8!/(3!2!3!)