1. Combinations of multisets
- k개의 type이 있고, infinite repetition number를 가진 경우
그 중 r개를 선택해서 만들 수 있는 조합의 개수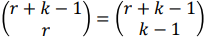
예제16 : 12개 박스에 8가지 도넛을 넣을 때 몇 개의 조합이 가능한가?
r =12, k=8인 경우에 해당한다.
따라서 C(12 + 8-1, 12) = C(19, 12)예제17 : 앞에는 작은 수, 뒤에는 큰 수가 나오게 배열할 때, 배열의 길이가 r이고 1~k를 이용하는 경우의 수는?
S = { 무한 1, 무한 2, .... , 무한 k } 에 해당되므로
C(r + k -1 , r) 과 일치한다.예제18 : 12개의 도넛을 사려고 하는데, 8가지중 최소한 1개씩은 고르고 싶을 때의 경우의 수는?
8개는 정해져있고 4개만 추가로 넣으면 되므로
C(4 + 8 -1 ,4) = C(11,4)예제19 : S를 {10ㆍa, 10ㆍb, 10ㆍc, 10ㆍd} multiset이라고 가정할 때(즉 40개가 있다.) 이 중 10개를 고르는 조합의 개수는 몇 개 인가? (= 10-combination)
단 a, b, c, d를 최소 1개씩은 포함해야 한다.
x1 + x2 + x3 + x4 = 10 인데 모두 1이상이니
positive integral solution의 개수에 해당한다. 따라서
y1 = x1 -1 , y2 = x2 -1 , y3 = x3 -1, y4 = x4 -1
로 치환이 성립하고
y1 + y2 + y3 + y4 = 6 으로 표현할 수 있다.
즉, nonnegative integral solution 이다.
C(6 + 4 -1 , 6) = C(9, 6)예제20 : x1 + x2 + x3 + x4 = 20
다음 등식의 integral solution 개수를 구하시오
단, x1 >= 3, x2 >=1, x3 >=0, x4 >=5 이다.
19번과 마찬가지로 치환을 통해 풀이 할 수 있다.
y1 = x1 - 3, y2 = x2 -1, y3 = x3, y4 = x4 -5
y1 + y2 + y3 + y4 = 11
C(11 + 4 -1, 11) = C(14, 11)예제21 : 주사위를 돌렸을 때 3개의 합이 9일 확률은?
x1 + x2 + x3 = 9
에서 1<= x <= 6 이라는 조건이 붙었다.
이를 y로 치환하면
i) y1 + y2 + y3 = 6
ii) 0<=y<=5
i) 를 토대로 경우의 수를 구하면
C(6 +3 -1, 6) = C(8, 6) 이지만
y가 6인 3가지 경우를 제외해야 하므로
C(8, 6) - 3 = 25 이다.
총 확률:
25/주사위 3번 6^3예제22 : 21번에서 합이 9보다 작을 확률은?
x1 + x2 + x3 <= 9 인 상황이다.
여기엔 slack 변수가 필요하다.
x4 = 9 - (x1 + x2 + x3)
-> x1 + x2 + x3 + x4 = 9
조건 : x4 >=0 , 나머지 x는 1<=x<=6
y1 + y2 + y3 + y4 = 6
조건 : y4 >=0, 나머지 y는 0<=y<=5
C(6 + 4 -1, 6) = C(10, 6) = 210
여기서 21번과 동일한 예외 상황을 제외하면
207 / 6^32. Inclusion-Exclusion Principle (포함-배제)
-
finite repetition number를 가진 S의 r-combination 수는
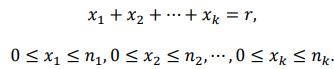과 동일하다. -
A1 ~ Am 의 여집합간의 교집합
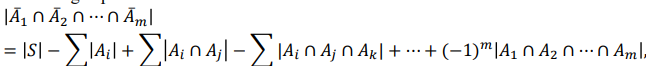S는 모든 집합의 크기 개수이지만 첫 항에서의 역할은 A1~Am 어디에도 들어가지 않는 부분이라고 할 수 있다.
(마지막 항은 R=m인 subset을 나타낸 것) -
아래 그림을 계산한 값은 0이다. 이항분포에서 (1-1)^n 와 같은 경우에 해당
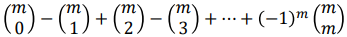
3. Combinations of multisets _2
예제23 : T= {3ㆍa, 4ㆍb, 5ㆍc} 에서 10-combination 의 개수를 구하라.
우선 무한이 아니므로 포함-배체 법칙을 이용해야한다.
A1= 적어도 4번인 경우, A2= 적어도 5, A3= 적어도 6
즉 A가 아닌 것(즉 여집합)들끼리의 교집합이 필요하다.
이를 수식으로 표현하면 다음과 같다.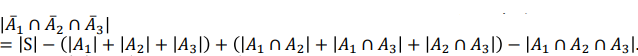
|S| = C(10 + 3-1, 10) = 66
|A1| = C(6 + 3 -1, 6) = 28
|A2| = C(5 + 3 -1, 5) = 21
|A3| = C(4 + 3 -1, 4) = 15
...예제24 : x1 + x2 + x3 + x4 = 18 이고
1<= x1 <= 5, -2<= x2 <= 4, 0<= x3 <= 5, 3<= x4 <=9 일 경우 integral solution의 개수는?
y1 = x1 -1, y2 = x2 + 2, y3 = x3, y4 = x4 -3
로 가정하면, y 부등식의 좌변은 모두 0이 된다.
y의 총합은 16이 되므로
|S| = C(16 + 4 -1, 16) = 969
이제 y1 <= 4, y2 <= 6, y3 <= 5, y4 <=6
경우와 반대되는 사건들이 동시에 일어날 수를 구해야한다.
|A1c ∩ A2c ∩ A3c ∩ A4c| = |A1 ∪ A2 ∪ A3 ∪ A4|c 이므로
|A| 들을 각각 구하고 2, 3, 4개의 교집합을 모두 구한뒤
전자의 총합에서 후자의 총합을 뺀 값이 Z라 할 때,
S-Z가 답이 될 것이다.4. Pascal's Triangle
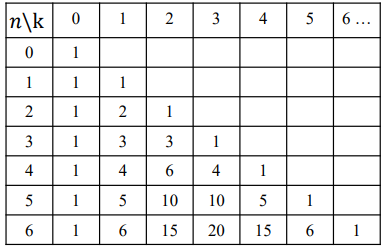여기서 2^n 은 같은 행에 있는 k값들의 합과 같다.
-
주요 관계식
(1)
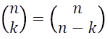
(2)
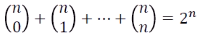
(3)
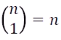
(4) triangular number : 삼각수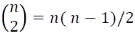
(5) tetrahedral number : 사면체수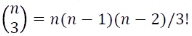
-
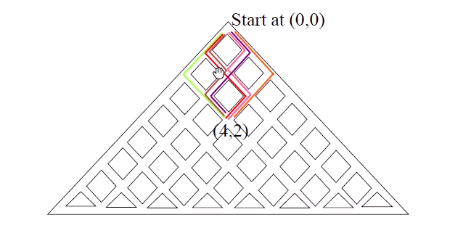
p(n, n) : n=0, k=0 인 원점이 임의의 점까지 가는데 필요한 경로의 개수
p(n, k) 까지 가는 경로의 개수는 p(n-1, k) + p(n-1, k-1) 과 같다.
즉, 다음과 같이 표현된다.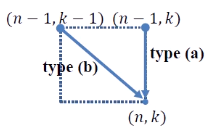
-
Block-Walking
(4, 2) 는 4칸을 지나 왔으며 방향을 2번 오른쪽으로 틀었음을 의미한다.
아래 그림에서는 모든 경로에서 오른쪽을 2번 선택한다.
